Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 109)
Câu 1: muốn đổi ra phân số thập phân ta làm thế nào
Phương pháp giải:
Thực hiện phép chia tử số cho mẫu số: .
Kết quả của phép chia chính là phân số thập phân.
Lời giải:
Chia .
Do đó, dưới dạng phân số thập phân là 1,5.
Câu 2: Viết các phân số sau đây theo thứ tự từ bé đến lớn
Phương pháp giải:
So sánh bằng cách so sánh tử và mẫu
Các phân số có giá trị gần : .
Giá trị càng nhỏ, phân số càng lớn.
Sắp xếp:
Sau khi so sánh, xếp các phân số theo thứ tự tăng dần.
Lời giải:
.
Vì
Câu 3: Làm phép chia (x3 − 3x2 + x − 3):(x − 3)
Phương pháp giải:
Phân tích đa thức x3 − 3x2 + x − 3 thành nhân tử có 1 nhân tử là (x - 3) và thực hiện phép chia.
Lời giải:
Câu 4: Cho tập hợp M = {1; 2; 3; 4; 5}. Số tập con gồm 2 phần tử của tập hợp M là
Phương pháp giải:
Xác định dạng bài toán:
Đây là bài toán chọn 2 phần tử từ tập hợp 5 phần tử mà không xét thứ tự.
Số cách chọn được tính bằng tổ hợp chập 2 của 5 phần tử.
Công thức tổ hợp:
, với là số phần tử của tập hợp và là số phần tử cần chọn.
Ở đây: , .
Tính toán:
Thay vào công thức để tìm số tập con.
Lời giải:
Số tập con có 2 phần tử của M là:
Phương pháp giải:
Đổi thời gian: Chuyển 2 giờ 24 phút thành đơn vị giờ để dễ tính toán.
Tính tổng vận tốc và tính vận tốc của từng người.
Lời giải:
Đổi 2 giờ 24 phút = 2,4 (giờ)
Tổng vận tốc của người A và vận tốc của người B là:
62,4 : 2,4 = 26 (km/h)
Vận tốc của người thứ nhất là:
(26 - 3) : 2 = 11,5 (km/h)
Vận tốc của người thứ hai là:
11,5 + 3 = 14,5 (km/h)
Đs...
Phương pháp giải:
Nhận xét hình học:
Tứ giác là hình chữ nhật vì các góc và đều bằng .
Tâm của hình chữ nhật là trung điểm của cả và .
Xét tam giác :
là đường cao, là trung điểm của .
Chứng minh , tức là tâm đường tròn ngoại tiếp tam giác .
Kết luận góc vuông:
Dựa vào tính chất đường kính trong đường tròn ngoại tiếp, vuông tại .
Lời giải:
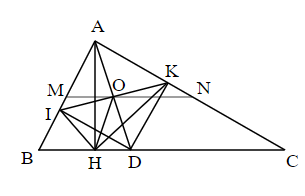
a) 2 đoạn AD và IK cắt nhau ở O. Nối O với H.
Xét tứ giác AIDK: => Tứ giác AIDK là hình chữ nhật
O là tâm của hình chữ nhật AIDK => O là trung điểm AD & IK; OA=OD=OI=OK
Xét AHD: ; O là trung điểm AD => OH=OA=OD
=> OH=OI=OK. Trong HIK có: O là trung điểm IK; OH=OI=OK
=> HIK vuông tại H => (đpcm).
Câu 7: Cho ▲ABC vuông cân tại A, biết BC = 10cm. Tính AB
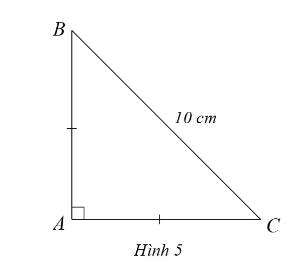
Phương pháp giải:
Áp dụng định lý Pytago: Cho tam giác ABC vuông tại A. Có độ dài cạnh AB = a, AC = b, BC = c. Áp dụng định lý Pytago, công thức về mối liên hệ giữa các cạnh trong tam giác được biểu diễn như sau:
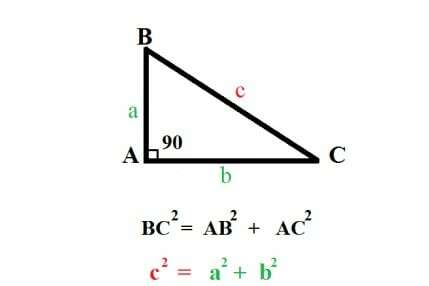
Lời giải:
ΔABC vuông cân tại A
=>
=>
=>
=>
=>
Câu 8: x0 trong toán học là gì?
Phương pháp giải:
Xác định vai trò của :
thường được dùng để biểu diễn một giá trị cụ thể của trong các bài toán toán học.
Nó có thể là nghiệm của một phương trình, một giá trị ban đầu, hoặc một mốc để khảo sát.
Ý nghĩa phổ biến của :
Trong phương trình: là một nghiệm cụ thể .
Trong giải tích: có thể là điểm khảo sát trong đạo hàm, tích phân hoặc giới hạn .
Trong bài toán thực tế: là một giá trị khởi đầu (ví dụ, ở thời điểm ).
Lời giải:
trong toán học là một giá trị cụ thể của , được dùng để:
Xác định nghiệm của phương trình.
Làm mốc khảo sát trong bài toán giới hạn, đạo hàm hoặc tích phân.
Biểu diễn một giá trị ban đầu trong bài toán thực tế.
Ví dụ:
Phương trình , là một nghiệm.
Giới hạn , là điểm khảo sát.
Trong bài toán chuyển động: là vị trí ban đầu của vật.
Câu 9: Cho S = 4 + 42 + 43 + ... + 49 + 410. Tìm số tự nhiên x biết: 3S + 4 = 4x
Phương pháp giải:
Tính tổng :
, là tổng của một cấp số nhân với:
Số hạng đầu .
Công bội .
Số hạng cuối .
Nhân với 4:
Tính .
Lấy hiệu :
.
Suy ra .
Sử dụng phương trình:
Từ đề bài , thay vào, giải để tìm .
Lời giải:
Câu 10: Chứng minh rằng: 76 + 75 - 74 chia hết cho 55
Phương pháp giải:
Đưa về dạng tích bằng cách đặt làm nhân tử chung.
Tính tổng trong ngoặc để thu được .
Nhận xét:
, nên biểu thức trở thành .
chia hết cho 55 vì có thừa số 55.
Lời giải:
76 + 75 - 74
= 74.(72 + 7 - 1)
= 74.(49 + 7 - 1)
= 74.55 chia hết cho 55
=> 76 + 75 - 74 chia hết cho 55
Câu 11: Phân tích đa thức thành nhân tử:
Phương pháp giải:
Nhóm các hạng tử có chung nhân tử để dễ dàng đặt nhân tử chung.
Tìm nhân tử chung của từng nhóm, rồi đặt nhân tử chung ra ngoài dấu ngoặc.
Nếu các nhóm có nhân tử giống nhau, đặt tiếp nhân tử chung để hoàn thành việc phân tích.
Lời giải:
Một số phương pháp phân tích đa thức thành nhân tử:
Phương pháp đặt nhân tử chung
+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.
( lưu ý tính chất: A = -(-A)).
Phương pháp dùng hằng đẳng thức
+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.
+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.
Phương pháp nhóm hạng tử
+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.
+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thế phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.
+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.
Chú ý
+ Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.
+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).
+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.
+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.
Phối hợp nhiều phương pháp
Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:
+ Đặt nhân tử chung
+ Dùng hằng đẳng thức
+ Nhóm nhiều hạng tử và phối hợp chúng
⇒ Để phân tích đa thức thành nhân tử.
Chú ý
Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.
Câu 12: Phân tích đa thức thành nhân tử:
a)
b)
c)
Phương pháp giải:
Nhóm hạng tử: Nhóm các hạng tử có yếu tố chung.
Rút yếu tố chung ra ngoài
Lời giải:
a)
b)
c)
Một số phương pháp phân tích đa thức thành nhân tử:
Phương pháp đặt nhân tử chung
+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.
( lưu ý tính chất: A = -(-A)).
Phương pháp dùng hằng đẳng thức
+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.
+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.
Phương pháp nhóm hạng tử
+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.
+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thế phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.
+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.
Chú ý
+ Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.
+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).
+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.
+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.
Phối hợp nhiều phương pháp
Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:
+ Đặt nhân tử chung
+ Dùng hằng đẳng thức
+ Nhóm nhiều hạng tử và phối hợp chúng
⇒ Để phân tích đa thức thành nhân tử.
Chú ý
Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.
Câu 13: Tìm n, biết: 2n+1 + 2n = 96
Phương pháp giải:
Rút nhân tử chung:
Chuyển đổi:
So sánh số mũ:
Lời giải:
Câu 14: Tính nhanh: 58 x 75 + 58 x 50 - 58 x 25
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để tính nhanh.
Lời giải:
Ta có : 58 x 75 + 58 x 50 - 58 x 25
= 58 x ( 75 + 50 - 25 )
= 58 x 100
= 5800
Phương pháp tính nhanh giá trị biểu thức
Dạng 1: Nhóm các số hạng trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn... rồi cộng (hoặc trừ) các kết quả lại.
Trong một bài toán về tính giá trị biểu thức, học sinh cần quan sát xem có nhóm các số nào có tổng hoặc hiệu là các số tròn chục, tròn trăm, tròn nghìn hay không, từ đó nhóm các số đó lại để tính một cách thuận tiện nhất.
Công thức tổng quát: a + b + c = (a + b) + c
a - b - c = (a - b) - c
Dạng 2: Vận dụng tính chất một số nhân với một tổng, một số nhân với một hiệu, một tổng chia cho một số, một hiệu chia cho một số.
Trong các phép tính tổng (hoặc hiệu), tích ( hoặc thương), học sinh cần chú ý các tính chất giao hoán, tính chất kết hợp của các số để có thể tính một cách thuận tiện nhất.
Công thức tổng quát:
- Một số nhân với một tổng: a x (b + c) = a x b + a x c
a x b + a x c = a x (b + c)
- Một số nhân với một hiệu: a x (b - c) = a x b - a x c
a x b - a x c = a x (b - c)
- Một tổng chia cho một số: (a + b + c) : d = a : d + b : d + c : d
Ví dụ: Tính nhanh giá trị của biểu thức sau
(18 + 45 + 63) : 9
= 18 : 9 + 45 : 9 + 63 : 9
= 2 + 5 + 7
= 14
- Một hiệu chia cho một số: (a - b - c) : d = a : d - b : d - c : d
Với các biểu thức chưa có thừa số chung, cần xem xét có thể phân tích một số ra một tích hoặc phân tích một tích ra các thừa số, từ đó làm xuất hiện thừa số chung được không.
Dạng 3: Vận dụng các tính chất: một số nhân với 0, một số nhân với 1, một số chia cho 1, 0 chia cho một số.
Trong các phép tính giá trị biểu thức, học sinh cần chú ý quan sát có biểu thức nào kết hợp các số có cho kết quả đặc biệt như 0 hoặc 1 hay không, từ đó tính bằng cách thuận tiện nhất.
Tính chất đặc biệt:
Một số nhân với 0 luôn cho kết quả bằng 0
Một số nhân với 1 luôn cho kết quả bằng chính số đó
Một số chia cho 1 luôn cho kết quả bằng chính số đó
Số 0 chia cho một số luôn cho kết quả bằng 0
Công thức tổng quát:
a x 0 = 0
a x 1 = a
a : 1 = a
0 : a = 0
Dạng 4: Vận dụng kiến thức về dãy số để tính giá trị biểu thức bằng cách thuận tiện nhất.
Vận dụng chủ yếu trong các dạng bài toán nâng cao về dãy số cách đều.
Công thức tổng quát:
Cách tìm số hạng của một dãy số cách đều: Số các số hạng = (Số cuối - Số đầu) : Khoảng cách + 1
Cách tính nhanh tổng của một dãy số cách đều:
Bước 1: Tính số các số hạng của dãy số cách đều (Theo công thức nêu trên)
Bước 2: Tính số cặp số của dãy số bằng cách lấy kết quả ở bước 1 chia cho 2 (Trường hợp dư 1 thì xem xét không ghép cặp 1 số)
Bước 3: Nhóm các cặp số hạng và tính tổng giá trị của cặp số (Chú ý có cặp số nào cho kết quả đặc biệt không, thông thường hay nhóm số đầu với số cuối)
Bước 4: Tính tổng dãy số bằng cách nhân kết quả ở bước 2 với kết quả ở bước 3, cộng thêm số không ghép cặp nếu có (tính tích số các cặp số nhân với tổng của một cặp số).
Phương pháp giải:
Gọi là tia phân giác của .
Sử dụng tính chất góc vuông:
và .
Suy ra: .
Do đó, cũng là tia phân giác của .
Lời giải:
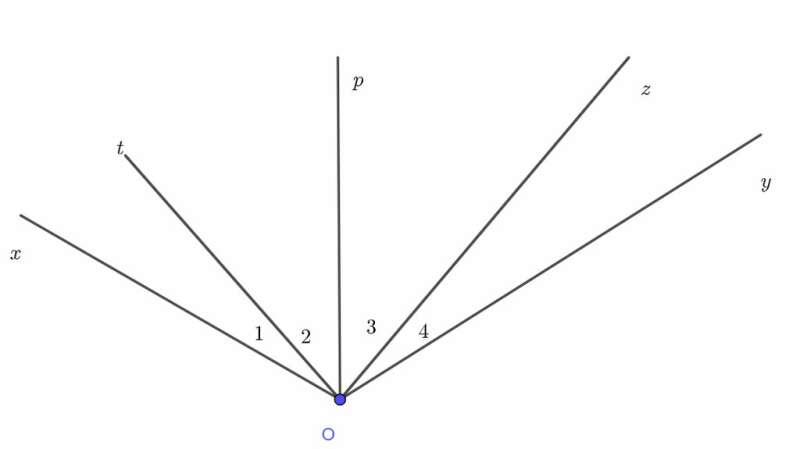
Gọi Op là tia phân giác của tOz
ta có : mà ta có
Vậy Op cũng là tia phân giác của xOy
Phương pháp giải:
Chia số và làm tròn kết quả đến 1 chữ số thập phân.
· Khi làm tròn số thập phân đến hàng phần mười, ta so sánh chữ số hàng phần trăm với 5. Nếu chữ số hàng phần trăm bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.
· Khi làm tròn số thập phân đến hàng phần trăm, ta so sánh chữ số hàng phần nghìn với 5. Nếu chữ số hàng phần nghìn bé hơn 5 thi làm tròn xuống, còn lại thì làm tròn lên.hi làm tròn số thập phân đến số tự nhiên gần nhất, ta so sánh chữ số ở hàng phần mười với 5. Nếu chữ số hàng phần mười bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.
Lời giải:
100 : 6 = 16,666
16,666 = 16,7 (làm tròn số)
Phương pháp giải:
Sử dụng công thức tính lãi kép, nhập vốn và lãi tháng trước thành vốn của tháng sau.
Lời giải:
Sau tháng thứ nhất người đó thu được cả vốn lẫn lãi là :
50.000.000 + 50.000.000 . 0,6% = 50.300.000 ( đồng )
Sau tháng thứ 2 người đó thu được số tiền là :
50.300.000 + 50.300.000 . 0,6% = 50.601.800 ( đồng )
Đáp số : 50.601.800 (đồng)
Một số dạng toán về lãi suất
Dạng 1: Bài toán tiết kiệm (Thể thức lãi kép không kỳ hạn)
Một người gửi vào ngân hàng số tiền đồng, lãi suất mỗi tháng theo hình thức lãi kép, gửi theo phương thức không kì hạn. Tính số tiền cả vốn lẫn lãi mà người đó nhận được sau tháng?
Phương pháp xây dựng công thức:
Gọi là số tiền cả vốn lẫn lãi sau tháng. Ta có:
- Sau 1 tháng .
- Sau 2 tháng
…
- Sau tháng
Vậy số tiền cả vốn lẫn lãi người đó có được sau tháng là:

Lãi suất thường được cho ở dạng nên khi tính toán ta phải tính rồi mới thay vào công thức.
Dạng 2: Bài toán tiết kiệm (Thể thức lãi kép có kỳ hạn)
Một người gửi vào ngân hàng số tiền đồng, lãi suất mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn tháng. Tính số tiền cả vốn lẫn lãi mà người đó nhận được sau kì hạn?
Phương pháp:
Bài toán này tương tự bài toán ở trên, nhưng ta sẽ tính lãi suất theo định kỳ tháng là: .
Sau đó áp dụng công thức với là số kì hạn.

Trong cùng một kì hạn, lãi suất sẽ gống nhau mà không được cộng vào vốn để tính lãi kép.
Dạng 3: Bài toán tích lũy (Hàng tháng (quý, năm,…) gửi một số tiền cố định vào ngân hàng)
Một người gửi vào ngân hàng số tiền đồng mỗi tháng với lãi suất mỗi tháng là . Hỏi sau tháng, người đó có tất cả bao nhiêu tiền trong ngân hàng?
Phương pháp xây dựng công thức:
Gọi là số tiền có được sau tháng.
- Cuối tháng thứ 1: .
- Đầu tháng thứ 2:
- Cuối tháng thứ 2:
…
- Đầu tháng thứ N:
- Cuối tháng thứ .
Vậy sau tháng, số tiền cả vốn lẫn lãi người đó có được là:
Dạng 4: Bài toán trả góp.
Một người vay ngân hàng số tiền đồng, lãi suất định kì là . Tìm số tiền mà người đó phải trả cuối mỗi kì để sau kì hạn là hết nợ.
Phương pháp xây dựng công thức:
- Sau 1 tháng, số tiền gốc và lãi là , người đó trả đồng nên còn:
- Sau 2 tháng, số tiền còn nợ là:
- Sau 3 tháng, số tiền còn nợ là:
- Sau tháng, số tiền còn nợ là: .
Vậy sau tháng, người đó còn nợ số tiền là:

Khitrả hết nợ thì số tiền còn lại bằng nên ta có:
Câu 18: Tính bằng cách thuận tiện: 365 x 33 - 365 x 11 - 365 x 2
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để tính nhanh và rút gọn.
1. Tính chất giao hoán:
a + b = b + a và a x b = b x a
2. Tính chất kết hợp:
(a + b) + c = a + (b + c) và (a x b) x c = a x (b x c)
3. Nhân với 1 và chia cho 1:
a x 1 = a ; a : a = 1 và a : 1 = a
4. Cộng và nhân với 0:
a + 0 = a và a x 0 = 0
5. Nhân một số với một tổng hoặc với một hiệu:
a x (b + c) = a x b + a x c và a x (b - c) = a x b - a x c
Lời giải:
365 x 33 - 365 x 11 - 365 x 2
= 365 x (33 - 11 - 2)
= 365 x 20
= 365 x 2 x 10
= 730 x 10
= 7300
Câu 19: Tính giá trị biểu thức tại x = 3, y =
Phương pháp giải:
Thay giá trị và vào biểu thức đã cho.
Tính toán từng phần theo thứ tự ưu tiên các phép toán.
Rút gọn kết quả.
Lời giải:
A =
Khi x = 3 và y= thì
Phương pháp chung
Để tính giá trị biểu thức, ta làm như sau:
Bước 1: Xác định giá trị đề bài đã cho.
Bước 2: Thay giá trị đề bài đã cho vào biểu thức.
Bước 3: Thực hiện phép tính.
Chú ý:
- Đối với biểu thức không có dấu ngoặc chỉ có phép cộng, trừ (hoặc nhân, chia), ta thực hiện các phép tính theo thứ tự từ trái qua phải.
- Đối với biểu thức không có dấu ngoặc và có cả các phép cộng, trừ, nhân, chia, ta thực hiện các phép tính theo thứ tự:
Lũy thừa Nhân, chia Cộng, trừ
- Đối với biểu thức có dấu ngoặc ta thực hiện theo thứ tự:
Ngoặc tròn () Ngoặc vuông [] Ngoặc nhọn {}
Câu 20: Tìm x biết: x = 24 + 32 . 32
Phương pháp giải:
Tính giá trị từng lũy thừa.
Thực hiện các phép nhân và cộng theo thứ tự.
Lời giải:
x = 24 + 32 . 32
x = 16 + 9 . 9
x = 16 + 81
x = 97
Phương pháp chung
- Vận dụng linh hoạt các công thức, tính chất, phép tính về lũy thừa để tính nhanh và hợp lý.
- Kết hợp hài hòa các phương pháp tính toán trong khi biến đổi.
- Các công thức cần nhớ
Với: x, y ∈ Q; m, n ∈ N
Quy ước: a1 = a; a0 = 1 (a ≠ 0)
Câu 21: P = Chứng minh các biểu thức sau ko phụ thuộc vào x
Phương pháp giải:
Biến đổi các biểu thức trong căn: Thay các biểu thức trùng lặp và sử dụng các công thức lượng giác để rút gọn.
Tính toán các hằng số: Sau khi thay và tính toán, ta sẽ có biểu thức không phụ thuộc vào biến .
Đưa về dạng hằng số: Kết quả cuối cùng là một hằng số, không còn chứa biến .
Lời giải:
Phương pháp giải:
Nhóm và đặt nhân tử chung: Biến đổi phương trình ban đầu để đưa về dạng tích của hai biểu thức.
Xét các giá trị nguyên: Do , xét các giá trị nguyên của các tích bằng cách phân tích hoặc thành tích của hai số nguyên.
Lập bảng: Thử tất cả các giá trị nguyên khả dĩ và tính tương ứng giá trị của và .
Lấy các giá trị thỏa mãn phương trình.
Lời giải:
Vì:
Mà: 5 = 5 . 1 <=> (-1) . (-5)
Ta có bảng:
| y + 2 | 1 | 5 | -1 | -5 |
| x - y | 5 | 1 | -5 | -1 |
| y | -1 | 3 | -3 | 7 |
| x | 7 | 3 | -3 | 1 |
Phương pháp giải:
Xác định điều kiện xác định (ĐKXĐ):
Đảm bảo các biểu thức trong căn bậc hai và căn bậc ba có nghĩa.
Phân tích các biểu thức chứa căn thành dạng dễ giải hơn.
Quy đồng hoặc đặt ẩn phụ nếu cần để đưa phương trình về dạng đơn giản hơn.
Giải phương trình.
Tìm được nghiệm thỏa mãn phương trình và ĐKXĐ.
Lời giải:
ĐKXĐ:
PT
Với thuộc đkxđ, dễ thấy biểu thức trong ngoặc vuông
Phương pháp giải:
Phân tích bài toán:
Đọc dữ liệu từ tệp dulieu.inp.
Tính tổng của từng bộ số nguyên trong tệp (mỗi bộ gồm 2 số nguyên trên một dòng).
Ghi kết quả vào tệp tong.out, mỗi kết quả trên một dòng.
Sử dụng chương trình con:
Viết một chương trình con (hàm) để tính tổng hai số nguyên.
Sử dụng chương trình chính để thực hiện đọc/ghi tệp và gọi chương trình con.
Lời giải:
#python
# Hàm tính tổng của hai số nguyên
def tinh_tong(a, b):
return a + b
# Chương trình chính
def xu_ly_tap_tin():
# Mở tệp đọc dữ liệu
with open('dulieu.inp', 'r') as file_in:
lines = file_in.readlines()
# Mở tệp ghi kết quả
with open('tong.out', 'w') as file_out:
for line in lines:
# Tách các số nguyên trên mỗi dòng
a, b = map(int, line.split())
# Tính tổng bằng chương trình con
tong = tinh_tong(a, b)
# Ghi kết quả vào tệp
file_out.write(str(tong) + '\n')
# Gọi chương trình chính
xu_ly_tap_tin()
Phương pháp giải:
Xét dấu của phân số:
Phân số là một số âm.
Phân số là một số dương.
So sánh giá trị:
Một số dương luôn lớn hơn một số âm.
Lời giải:
Ta có: là một số dương
=>
a)
b)
Phương pháp giải:
Xác định điều kiện xác định.
Giải phương trình bậc hai, đối chiếu nghiệm với điều kiện ban đầu.
Lời giải:
a)
b)
Giải pt (1)
Pt
Giải pt (2)
Pt
Vậy nghiệm pt là
Lý thuyết Phương trình chứa căn
1. Các điều kiện và tính chất cơ bản
+ √A có nghĩa khi A ≥ 0
+ √A ≥ 0 với A ≥ 0
+ √A2 = 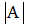
+ 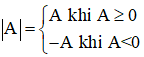
+ √A2 = 0 ⇔ A = 0
+ √AB = √A.√B khi A ≥ 0; B ≥ 0
+ √AB = √-A.√-B khi A ≤ 0; B ≤ 0
2. Các dạng phương trình chứa căn
+ 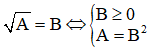
+ 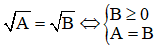
+ √A + √B = 0
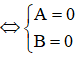
+ 3√A = B ⇔ A = B3
+ 3√A = 3√B ⇔ A = B
Phương pháp giải:
Vì nằm cùng phía với đối với , nên nằm giữa và ; là trung điểm của .
Sử dụng tính chất đoạn thẳng: .
Biến đổi: . (đpcm)
Lời giải:
C nằm cùng phía với B đối với A => B nằm giữa A và C (1)
M là trung điểm AB => M nằm giữa A và B (2)
Từ (1) và (2) => B nằm giữa C và M
Ta có:
(đpcm)
Câu 28: Cho biết cos∝ = 12/13 giá trị của tan ∝ là:
Phương pháp giải:
Công thức lượng giác cơ bản
Cho góc α (0° ≤ α ≤ 180°), ta có các công thức lượng giác cơ bản sau:
(1) cos2α + sin2α = 1;
(2) tanα.cotα = 1; với 0° < α < 180°, α ≠ 90°;
(3) với α ≠ 90°;
(4) với 0° < α < 180°.
Lời giải:
Phương pháp giải:
Phân tích các số ra thừa số nguyên tố.
BCNN là tích của các thừa số nguyên tố với số mũ lớn nhất.
Tính toán và kết luận.
Lời giải:
84 = 22.3.7
108 = 22.33
BCNN(84,108) = 22.33.7 = 4.27.7 = 756
Vậy BCNN của 84 và 108 là 756
Câu 30: a) Tìm các tập hợp Ư(8); Ư(12); Ư(15)
b) Tìm tập hợp B các bội của 7 nhưng không lớn hơn 50
c) Tìm tập hợp C các bội của 3 nhưng không quá 35.Tập hợp C có bao nhiêu phần tử ?
Phương pháp giải:
Tìm tập hợp ước của một số:
Phân tích các số thành ước nguyên dương, liệt kê toàn bộ các ước.
Tìm tập hợp bội:
Liệt kê các bội của số đã cho bằng cách nhân số đó với các số nguyên dương, dừng lại khi đạt giới hạn yêu cầu.
Xác định số phần tử của tập hợp bội:
Sử dụng công thức:
Lời giải:
a)
b)
c)
Tập hợp C có số phần tử là
(phần tử)
Câu 31: Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6
a, a + 5b
b, a + 17b
c, a - 13b
Phương pháp giải:
Biến đổi các biểu thức: , , .
Vì chia hết cho 6 và các số hạng , , đều chia hết cho 6.
Suy ra , , đều chia hết cho 6. (đpcm)
Lời giải:
a) a + 5b
Ta có: a + 5b = a - b + 6b
Do a - b chia hết cho 6
6b cũng chia hết cho 6
=> a + 5b chia hết cho 6 (đccm)
b) a + 17b
Ta có: a + 17b = a - b + 18b
Do a - b chia hết cho 6
18 chia hết cho 6 => 18b cũng chia hết cho 6
=> a + 17b chia hết cho 6 (đccm)
c) a - 13b
Ta có: (a - b) - 12b = a - 13b
Do a - b chia hết cho 6
12b cũng chia hết cho 6
=> a - 13b chia hết cho 6 (đccm)
Tính chất chia hết
Tính chất 1
Nếu 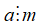
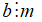
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết 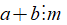
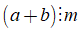
Chú ý:
• Tính chất 1 cũng đúng đối với một hiệu
• Tính chất 1 cũng đúng với một tổng nhiều số hạng
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Tính chất 2
Nếu 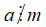
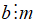
Nếu 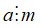
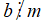
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết 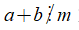
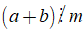
Chú ý:
• Tính chất 2 cũng đúng đối với một hiệu
• Tính chất 2 cũng đúng với một tổng nhiều số hạng, trong đó chỉ có một số hạng không chia hết cho m, các số hạng còn lại đều chia hết cho m:
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số , còn các số hạng còn lại đều chia hết cho số đó thì tổng đó không chia hết cho số đó.