Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 66)

Câu 1: Tìm số tự nhiên n thoả mãn 2.2² + 3.2³ + 4.2⁴ + ... + n.2ⁿ = 2ⁿ + 11

Lời giải:

Đặt A = 2.2² + 3.2³ + 4.2⁴ + ... + n.2ⁿ

Ta có: A = 2.2² + 3.2³ + 4.2⁴ + ... + n.2ⁿ

Suy ra 2A = 2(2.2² + 3.2³ + 4.2⁴ + ... + n.2ⁿ)

= 2.2³ + 3.2⁴ + 4.2⁵ + ... + n.2^{n + 1}

Do đó 2A - A = A = 2.2² + (3.2³ - 2.2³) + ... + (n - n + 1).2ⁿ - n.2^{n + 1}

= 2.2² + 2³ + 2⁴ + ... + 2ⁿ -n.2^{n + 1}

= 2² + (2² + 2³ + 2⁴ + ... + 2^{n + 1}) - (n + 1) . 2^{n + 1}

Đặt B = 2² + 2³ + 2⁴ + ... + 2^{n + 1}

Suy ra 2B = 2³ + 2⁴ + 2⁵ + ... + 2^{n + 2}

Do đó 2B - B = B = 2^{n + 2} - 2²

⇒ B = 2^{n + 2} - 2² = 2² - 2^{n + 2} + 2² + (n + 1).2^{n + 1}

= (n + 1).2^{n + 1} - 2^{n + 2}

= 2^{n + 1}(n + 1 - 2)

= (n - 1).2ⁿ⁺¹ = 2(n - 1).2ⁿ

Mà A = 2(n - 1).2ⁿ = 2^{n + 11}

⇒ 2(n - 1) = 2¹¹ ⇒ n - 1 = 2¹⁰

⇒ n - 1 = 1024 ⇒ n = 1025

Vậy n = 1025.

Câu 2: Ba khối 6, 7 và 8 lần lượt có 300 học sinh, 276 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối là như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối đều không có ai lẻ hàng? Khi đó ở mỗi hàng dọc của mỗi khối có bao nhiêu học sinh?

Lời giải:

Do số hàng dọc của mỗi khối là như nhau nên số hàng dọc sẽ là ước chung của 300, 276, 252

Hơn nữa cần xếp nhiều nhất thành các hàng dọc để mỗi khối đều không có ai lẻ hàng nên số hàng là ƯCLN(300, 276, 252)

Ta có: 300 = 2² . 3 . 5²

276 = 2² . 3 . 23

252 = 2² . 3² . 7

ƯCLN(300, 276, 252) = 2² . 3 = 12

Vậy có thể xếp nhiều nhất học sinh của ba khối 6, 7 và 8 thành 12 hàng.

Khi đó ở mỗi hàng:

+) Khối 6 có 300 : 12 = 25 (học sinh)

+) Khối 7 có 276 : 12 = 23 (học sinh)

+) Khối 8 có 252 : 12 = 21 (học sinh) 

Câu 3: Một sân trường hình chữ nhật có nửa chu vi là 120 m. Chiều rộng bằng $\frac{3}{5}$ chiều dài. Hỏi diện tích của sân trường đó bằng bao nhiêu mét vuông, bao nhiêu ha?

Lời giải:

Ta có sơ đồ:

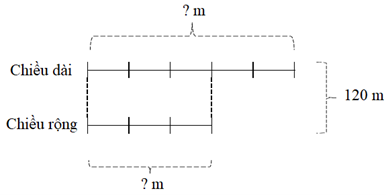
Theo sơ đồ, tổng số phần bằng nhau là:

3 + 5 = 8 (phần)

Chiều rộng sân trường đó là:

120 : (8 × 3) = 45 (m)

Chiều dài sân trường đó là:

120 - 45 = 75 (m)

Diện tích sân trường đó là:

75 × 45 = 3375 (m²)

Đổi 3 375 m² = 0,3375 ha

Đáp số: 3 375 m²; 0,3375 ha.

Câu 4: Cho bốn số nguyên dương a, b, c, d thỏa mãn a² + b² = c² + d². Chứng minh rằng a + b + c + d là hợp số.

Lời giải:

Ta có a² + b² = c² + d².

Suy ra a² + b² + c² + d² = 2(c² + d²) ⋮ 2   (1)

Xét A = (a² + b² + c² + d²) – (a + b + c + d).

= (a² – a) + (b² – b) + (c² – c) + (d² – d).

= a(a – 1) + b(b – 1) + c(c – 1) + d(d – 1).

Vì a và a – 1 là hai số nguyên liên tiếp nên tích a(a – 1) chia hết cho 2.

Tương tự như vậy, ta có b(b – 1) ⋮ 2, c(c – 1) ⋮ 2 và d(d – 1) ⋮ 2.

Khi đó A ⋮ 2   (2)

Từ (1), (2), suy ra a + b + c + d chia hết cho 2.

Mà a, b, c, d là các số nguyên dương.

Suy ra a + b + c + d > 2.

Vậy a + b + c + d là hợp số.

Câu 5: Cho x + y = 3. Tính giá trị biểu thức: A = x³ + x²y – 3x² + xy + y² – 4y – x + 3.

Lời giải:

Ta có A = x³ + x²y – 3x² + xy + y² – 4y – x + 3.

= (x³ + x²y – 3x²) + (xy + y² – 3y) – (x + y – 3).

= x²(x + y – 3) + y(x + y – 3) – (x + y – 3).

= (x + y – 3)(x² + y – 1).

= (3 – 3)(x² + y – 1).

= 0.(x² + y – 1).

= 0.

Vậy A = 0 khi x + y = 3.

Câu 6: Cho hình vuông, nếu giảm cạnh hình vuông đó đi 7 m thì diện tích giảm đi 84 m². Tính diện tích hình vuông ban đầu.

Lời giải:

Gọi cạnh hình vuông ban đầu là a (a > 0; m).

Cạnh hình vuông sau khi giảm đi 7 m là a – 7 (m).

Diện tích hình vuông ban đầu là: a × a.

Diện tích hình vuông sau khi giảm cạnh hình vuông đi 7 m là:

(a – 7) × (a – 7) = a × a – 84.

a × a – 7 × a – 7 × a + 7 × 7 = a × a – 84.

–14 × a + 49 = –84.

14 × a = 133.

a = 133 : 14.

a = 9,5 (m).

Diện tích hình vuông ban đầu là: 9,5 × 9,5 = 90,25 (m²).

Đáp số: 90,25 m².

Câu 7: Tìm cạnh của hình vuông nếu cạnh của hình vuông giảm đi 7 m thì diện tích giảm đi 84 m².

Lời giải:

Gọi cạnh hình vuông ban đầu là a (a > 0; m).

Cạnh hình vuông sau khi giảm đi 7 m là a – 7 (m).

Diện tích hình vuông ban đầu là: a × a.

Diện tích hình vuông sau khi giảm cạnh hình vuông đi 7 m là:

(a – 7) × (a – 7) = a × a – 84.

a × a – 7 × a – 7 × a + 7 × 7 = a × a – 84.

–14 × a + 49 = –84.

14 × a = 133.

a = 133 : 14.

a = 9,5 (m).

Đáp số: 9,5 m.

Câu 8: Tìm giá trị lớn nhất của biểu thức A = –2x² + 12x – 11.

Lời giải:

Ta có A = –2x² + 12x – 11.

= –2(x² – 6x + 9) + 7.

= –2(x – 3)² + 7.

Ta có (x – 3)² ≥ 0, ∀x ∈ ℝ.

⇒ –2(x – 3)² ≤ 0, ∀x ∈ ℝ.

⇒ –2(x – 3)² + 7 ≤ 7, ∀x ∈ ℝ.

Dấu “=” xảy ra ⇔ x = 3.

Vậy giá trị lớn nhất của A bằng 7 khi và chỉ khi x = 3.

Câu 9:

a) Tìm giá trị nhỏ nhất của biểu thức A = 2x² + 12x + 11.

b) Tìm giá trị lớn nhất của biểu thức B = –x² + 18x + 19.

Lời giải:

a) A = 2x² + 12x + 11.

= 2(x² + 6x + 9) – 7.

= 2(x + 3)² – 7.

Ta có (x + 3)² ≥ 0, ∀x ∈ ℝ.

⇔ 2(x + 3)² ≥ 0, ∀x ∈ ℝ.

⇔ 2(x + 3)² – 7 ≥ –7, ∀x ∈ ℝ.

Dấu “=” xảy ra ⇔ x = –3.

Vậy giá trị nhỏ nhất của A bằng –7 khi và chỉ khi x = –3.

b) B = –x² + 18x + 19.

= –(x² – 18x + 81) + 100.

= –(x – 9)² + 100.

Ta có (x – 9)² ≥ 0, ∀x ∈ ℝ.

⇔ –(x – 9)² ≤ 0, ∀x ∈ ℝ.

⇔ –(x – 9)² + 100 ≤ 100, ∀x ∈ ℝ.

Dấu “=” xảy ra ⇔ x = 9.

Vậy giá trị lớn nhất của B bằng 100 khi và chỉ khi x = 9.

Câu 10:

a) Nêu cách xác định hình chiếu của một điểm A lên đường thẳng d.

b) Nêu cách xác định hình chiếu của một điểm A lên mặt phẳng (P).

Lời giải:

a) Cách xác định hình chiếu của một điểm A lên đường thẳng d.

– Viết phương trình mặt phẳng (P) chứa điểm A và vuông góc với d.

– Tìm H là giao điểm của d và (P).

Suy ra H là hình chiếu của A trên d.

b) Cách xác định hình chiếu của một điểm A lên mặt phẳng (P).

– Viết phương trình đường thẳng đi qua A và vuông góc với (P).

– Tìm H là giao điểm của d và (P).

Suy ra H là hình chiếu của A trên (P).

Câu 11: Cách vẽ hình chiếu của một điểm trên một cạnh.

Lời giải:

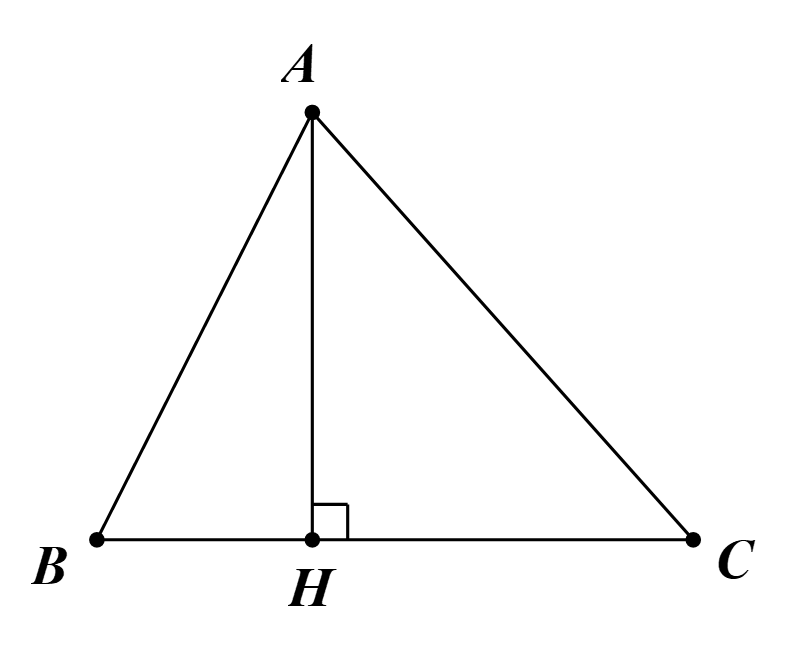
Giả sử ta cần vẽ hình chiếu của một điểm A trên cạnh BC, ta kẻ một đường thẳng đi qua điểm A và vuông góc với BC, đường thẳng này cắt BC tại H.

Vậy H là hình chiếu của một điểm A trên cạnh BC.

Câu 12: Tìm số nguyên dương n, biết: 121 ≥ 11ⁿ ≥ 1.

Lời giải:

Ta có 121 ≥ 11ⁿ ≥ 1.

⇔ 11² ≥ 11ⁿ ≥ 11⁰.

⇔ 2 ≥ n ≥ 0.

Vì n là số nguyên dương nên ta nhận n ∈ {1; 2}.

Vậy n ∈ {1; 2} thỏa mãn yêu cầu bài toán.

Câu 13: Thực hiện phép tính: 5⁶ : 5⁴ + 2³ . 2² – 1²⁰¹⁷.

Lời giải:

Ta có 5⁶ : 5⁴ + 2³ . 2² – 1²⁰¹⁷.

= 5^{6 – 4} + 2^{3 + 2} – 1.

= 5² + 2⁵ – 1.

= 25 + 32 – 1.

= 57 – 1.

= 56.

Câu 14: Liệt kê các phần tử của tập hợp sau:

a) A = {(x; x²) | x ∈ {–1; 0; 1}}.

b) B = {(x; y) | x² + y² ≤ 2 và x, y ∈ ℤ}.

Lời giải:

a) Với x = –1, ta có x² = 1.

Với x = 0, ta có x² = 0.

Với x = 1, ta có x² = 1.

Vậy A = {(–1; 1), (0; 0), (1; 1)}.

b) Vì x² + y² ≤ 2 và x, y ∈ ℤ nên x ∈ {–1; 0; 1}.

Với x = –1, ta có y² ≤ 2 – x² = 1.

⇔ –1 ≤ y ≤ 1.

Mà y ∈ ℤ nên y ∈ {–1; 0; 1}.

Vì vậy ta có các phần tử sau thuộc tập hợp B trong trường hợp x = –1 là: (–1; –1), (–1; 0), (–1; 1).

Ta thực hiện tương tự như vậy với các trường hợp x = 0, x = 1.

Vậy B = {(–1; –1), (–1; 0), (–1; 1), (0; –1), (0; 0), (0; 1), (1; –1), (1; 0), (1; 1)}.

Câu 15: Tính tổng B = 1 + 5 + 5² + 5³ + ... + 5¹⁵⁰.

Lời giải:

Ta có B = 1 + 5 + 5² + 5³ + ... + 5¹⁵⁰.

⇒ 5B = 5 + 5² + 5³ + 5⁴ + ... + 5¹⁵¹.

Khi đó 5B – B = (5 + 5² + 5³ + 5⁴ + ... + 5¹⁵¹) – (1 + 5 + 5² + 5³ + ... + 5¹⁵⁰).

⇒ 4B = (5 – 5) + (5² – 5²) + (5³ – 5³) + ... + (5¹⁵⁰ – 5¹⁵⁰) + 5¹⁵¹ – 1.

⇒ 4B = 5¹⁵¹ – 1.

Vậy $B=\frac{5^{151}-1}{4}$ .

Câu 16: Chứng tỏ rằng B = 1 + 5 + 5² + ... + 5⁷ + 5⁸ chia hết cho 31.

Lời giải:

Ta có B = 1 + 5 + 5² + ... + 5⁷ + 5⁸.

= (1 + 5 + 5²) + (5³ + 5⁴ + 5⁵) + (5⁶ + 5⁷ + 5⁸).

= 31 + 5³.(1 + 5 + 5²) + 5⁶.(1 + 5 + 5²).

= 31 + 5³.31 + 5⁶.31.

= 31.(1 + 5³ + 5⁶).

Ta có 31 ⋮ 31 (hiển nhiên).

Suy ra 31.(1 + 5³ + 5⁶) ⋮ 31.

Vậy B ⋮ 31.

Câu 17: Một đội công nhân gồm 40 người đã làm xong đoạn đường dài 1600 m hết 10 ngày. Nay công ty cử thêm 60 người nữa xuống làm tiếp đoạn đường dài 3200 m thì hoàn thành công việc trong bao lâu? (Biết năng suất lao động của mỗi người là như nhau).

Lời giải:

Ta có 3200 m gấp 1600 m số lần là:

3200 : 1600 = 2 (lần)

Nếu 40 người làm xong đoạn đường 3200 m thì hết số ngày là:

10 × 2 = 20 (ngày)

1 người làm xong 3200 m đường hết số ngày là:

20 × 40 = 800 (ngày)

Nếu có thêm 60 người thì làm xong đoạn đường 3200 m hết số ngày là:

800 : (40 + 60) = 8 (ngày)

Đáp số: 8 ngày.

Câu 18: Xe thứ nhất chở được 9 tấn xi-măng, xe thứ hai chở ít hơn xe thứ nhất 700 kg xi-măng. Hỏi cả hai xe chở được bao nhiêu tạ xi-măng?

Lời giải:

Đổi: 9 tấn = 9000 kg.

Xe thứ hai chở được số kg xi-măng là:

9000 – 700 = 8300 (kg)

Cả hai xe chở được số xi-măng là:

9000 + 8300 = 17300 (kg)

Đổi: 17300 kg = 173 tạ.

Đáp số: 173 tạ xi-măng.

Câu 19: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi M là trung điểm OO’. Qua A, kẻ đường thẳng vuông góc với AM, cắt các đường tròn (O) và (O’) tại C và D. Chứng minh rằng tam giác MCD cân.

Lời giải:

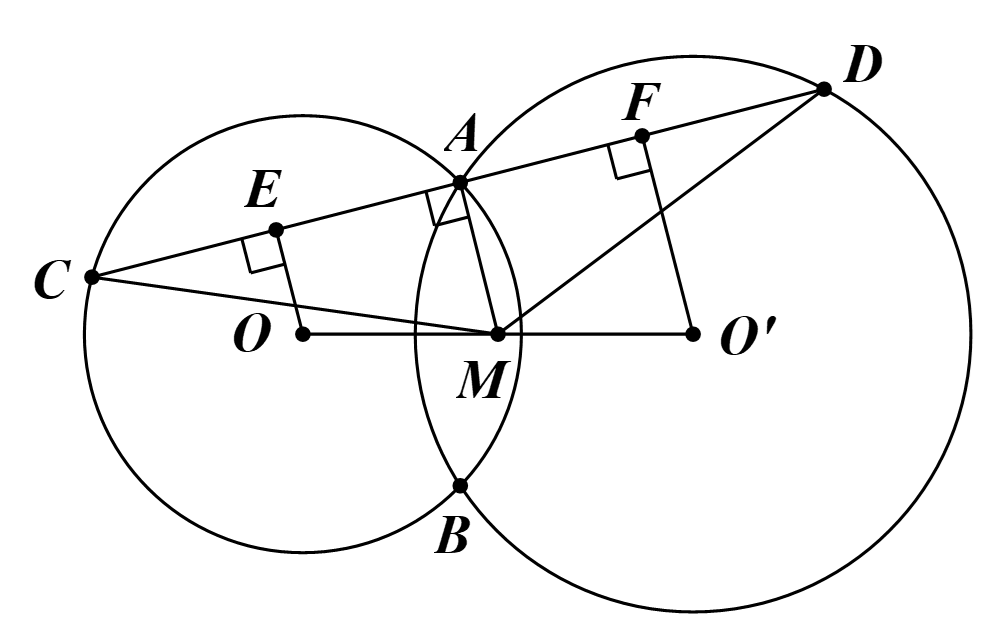
Gọi E là trung điểm của AC.

Suy ra AE = CE và OE ⊥ AC    (1)

Gọi F là trung điểm của AD.

Suy ra AF = FD và O’F ⊥ AD   (2)

Từ (1), (2), suy ra OE // O’F.

Mà MA ⊥ CD (do giả thiết).

Do đó OE // MA // O’F.

Khi đó tứ giác OO’FE là hình thang có MA là đường trung bình (vì M là trung điểm OO’).

Suy ra A là trung điểm của EF.

Do đó AE = AF.

Vì vậy 2AE = 2AF.

Suy ra AC = AD.

Khi đó A là trung điểm của CD.

Tam giác MCD có MA vừa là đường trung tuyến, vừa là đường cao.

Vậy tam giác MCD cân tại M.

Câu 20: Chứng minh rằng có vô số bộ ba số tự nhiên (a, b, c) sao cho a, b, c nguyên tố cùng nhau và số n = a²b² + b²c² + c²a² là số chính phương.

Lời giải:

Giả sử a, b, c là ba số tự nhiên lẻ liên tiếp có dạng a = 2k – 1, b = 2k + 1, c = 2k + 3, với k ∈ ℕ.

Khi đó bộ ba số tự nhiên (a, b, c) nguyên tố cùng nhau.

Ta có n = a²b² + b²c² + c²a²

= (2k – 1)²(2k + 1)² + (2k + 1)²(2k + 3)² + (2k + 3)²(2k – 1)²

= (4k² – 1)² + (2k + 3)².[(2k + 1)² + (2k – 1)²]

= 16k⁴ – 8k² + 1 + (4k² + 12k + 9).[(2k + 1 + 2k – 1)² – 2(2k + 1)(2k – 1)]

= 16k⁴ – 8k² + 1 + (4k² + 12k + 9).[16k² – 2(4k² – 1)]

= 16k⁴ – 8k² + 1 + (4k² + 12k + 9).(8k² + 2)

= 16k⁴ – 8k² + 1 + 32k⁴ + 8k² + 96k³ + 24k + 72k² + 18

= 48k⁴ + 96k³ + 72k² + 24k + 18 + 1.

Ta có 48; 96; 72; 24; 18 đều chia hết cho 3.

Suy ra 48k⁴; 96k³; 72k²; 24k; 18 đều chia hết cho 3, với k ∈ ℕ.

Khi đó tổng 48k⁴ + 96k³ + 72k² + 24k + 18 chia hết cho 3, với k ∈ ℕ.

Vì vậy 48k⁴ + 96k³ + 72k² + 24k + 18 + 1 chia cho 3 dư 1, với k ∈ ℕ.

Suy ra n là số chính phương.

Vậy ta có điều phải chứng minh.

Câu 21: Có bao nhiêu giá trị nguyên của m để hàm số y = mx⁴ + (m² – 4)x² + 2 có đúng một điểm cực đại và không có điểm cực tiểu?

A. 3.

B. 0.

C. 2.

D. 1.

Lời giải:

Đáp án đúng là: C

Hàm số đã cho có đúng một điểm cực đại và không có điểm cực tiểu.

$\iff \left\{\begin{array}{l}m<0\\ m^2-4\le 0\end{array}\right.\iff \left\{\begin{array}{l}m<0\\ -2\le m\le 2\end{array}\right.\iff -2\le m<0$.

Mà m ∈ ℤ nên m ∈ {–2; –1}.

Vậy có 2 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án C.

Câu 22: Chọn khẳng định đúng:

A. Hai đường tròn phân biệt có thể có hai điểm chung.

B. Hai đường tròn phân biệt có thể có ba điểm chung phân biệt.

C. Tâm đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác đó.

D. Đường thẳng d cắt đường tròn (O; R) khi khoảng cách từ tâm O đến đường thẳng d lớn hơn R.

Lời giải:

Đáp án đúng là: A

Phương án A đúng.

Phương án B sai vì 3 điểm chung phân biệt xác định được duy nhất 1 đường tròn nên nếu hai đường tròn (O) và (O’) có 3 điểm chung phân biệt thì hai đường tròn (O) và (O’) trùng nhau.

Phương án C sai vì trường hợp tam giác tù thì tâm đường tròn ngoại tiếp nằm bên ngoài tam giác đó.

Phương án D sai. Sửa lại: Đường thẳng d cắt đường tròn (O; R) khi khoảng cách từ tâm O đến đường thẳng d nhỏ hơn R.

Vậy ta chọn phương án A.

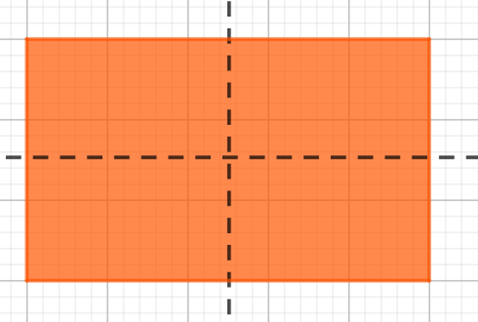
Câu 23: Hình chữ nhật (không phải hình vuông) có hai trục đối xứng là các đường nào?

Lời giải:

Hình chữ nhật (không phải hình vuông) có 2 trục đối xứng là đường thẳng đi qua trung điểm của các cặp cạnh đối diện của hình chữ nhật.

Câu 24: So sánh: 78¹² – 78¹¹ và 78¹¹ – 78¹⁰.

Lời giải:

Ta có 78¹² – 78¹¹ = 78¹¹.(78 – 1) = 78¹¹.77.

Lại có 78¹¹ – 78¹⁰ = 78¹⁰.(78 – 1) = 78¹⁰.77.

Vì 78¹¹ > 78¹⁰ nên 78¹¹.77 > 78¹⁰.77.

Vậy 78¹² – 78¹¹ > 78¹¹ – 78¹⁰.

Câu 25: So sánh bằng cách đưa về cùng cơ số: (0,343)⁸ và (–0,7)²⁶.

Lời giải:

Ta có (–0,7)²⁶ = (0,7)²⁶.

= (0,7)²⁴.(0,7)².

= [(0,7)³]⁸.(0,7)².

= (0,343)⁸.(0,7)².

Mà 0,7 < 1 nên (0,7)² < 1.

Do đó (0,343)⁸.(0,7)² < (0,343)⁸.

Suy ra (–0,7)²⁶ < (0,343)⁸.

Vậy (–0,7)²⁶ < (0,343)⁸.

Câu 26: Tìm số bộ (x, y, z, t) nguyên không âm thỏa mãn x + y + z + t = 40 và x, y, z, t là các số lẻ.

Lời giải:

Đặt $\left\{\begin{array}{l}x=2a-1\\ y=2b-1\\ z=2c-1\\ t=2d-1\end{array}\right.$ , với a, b, c, d là các số nguyên dương.

Suy ra 2(a + b + c + d) – 4 = x + y + z + t = 40.

Do đó a + b + c + d = 22.

Theo nguyên lí “chia kẹo Euler” thì số bộ nghiệm nguyên dương của phương trình trên là .

Vậy có 1330 số bộ (x, y, z, t) thỏa mãn yêu cầu bài toán.

Câu 27: Giải phương trình x² + 5x + 3 = 0.

Lời giải:

Ta có x² + 5x + 3 = 0   (*)

Ta có ∆ = b² – 4ac = 5² – 4.1.3 = 13 > 0.

Suy ra phương trình (*) có hai nghiệm phân biệt.

Hai nghiệm là: $\left[\begin{array}{l}{x}_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-5+\sqrt{13}}{2}\\ x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-5-\sqrt{13}}{2}\end{array}\right.$

Vậy tập nghiệm của phương trình đã cho là $S=\left\{\frac{-5\pm \sqrt{13}}{2}\right\}$ .

Câu 28: Cho phương trình x² – 5x + 3 = 0 có hai nghiệm x₁, x₂. Hãy lập phương trình bậc hai có hai nghiệm là y₁ = 2x₁ – x₂; y₂ = 2x₂ – x₁.

Lời giải:

Ta có x² – 5x + 3 = 0.

Theo Viet: S = x₁ + x₂ = 5.

                    P = x₁x₂ = 3.

Ta có:

⦁ y₁ + y₂ = 2x₁ – x₂ + 2x₂ – x₁ = x₁ + x₂ = 5.

⦁ $y_1{y}_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)=5x_1{x}_2-2\left(x_1^2+x_2^2\right)$ .

= 9x₁x₂ – 2(x₁ + x₂)² = 9.3 – 2.5² = –23.

Vậy y₁, y₂ là nghiệm của phương trình y² – 5y – 23 = 0.

Câu 29: So sánh bằng cách đưa về cùng cơ số: (–0,125)⁴ và (0,5)¹².

Lời giải:

Ta có (–0,125)⁴ = (0,125)⁴.

Lại có (0,5)¹² = [(0,5)³]⁴ = (0,125)⁴.

Vậy (–0,125)⁴ = (0,5)¹².

Câu 30: Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó.

Lời giải:

Ta có số phần tử của không gian mẫu khi dán 3 con tem vào 3 bức thư là hoán vị của 3 phần tử tức là: n(Ω) = 3! = 6

Gọi A là biến cố:"  hai bì thư trong ba bì thư đều có số thứ tự giống với số thứ tự giống với số thứ tự con tem đã dán vào"

Ta có lấy 1 bì thư có sao cho có số thứ tự giống với con tem đã dán vào nó có 1 cách, và bì thư còn lại cũng có một cách. Từ đó ta có số phần tử cho biến cố A là 1.

n(A) = 1

Xác suất để được biến cố trên là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{6}.$

Câu 31: Phân tích đa thức thành nhân tử: x² – x – xy – 2y²  + 2y.

Lời giải:

x² – x – xy – 2y²  + 2y

= x² – x + xy – 2y² + 2y – 2xy

= x(x – 1 + y) – 2y(y – 1 + x)

= (x – 2y)(x – 1 + y).

Câu 32: Hai đoạn ống nước có chiều dài lần lượt là 0,8 m và 1,35 m. Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là $\frac{2}{25}m.$ Hỏi đoạn ống nước mới dài bao nhiêu mét?

Lời giải:

Đoạn ống nước mới dài số mét là:

0,8 + 1,35 − $\frac{2}{25}$ = 2,15 − 0,08 = 2,07 (m).

Vậy đoạn ống nước mới dài 2,07 m.

Câu 33: Lúc 8h một người đi xe đạp chuyển động thẳng đều với vận tốc 12km/h gặp một người đi bộ đi ngược chiều chuyển động thẳng đều với vận tốc 4km/h trên cùng một đoạn đường. Lúc 8h30 người đi xe đạp dừng lại nghỉ 30 phút rồi quay lại đuổi theo người đi bộ với vận tốc cũ. Hỏi hai người gặp nhau ở đâu? Lúc nào?

Lời giải:

Ta viết tắt “giờ” là “h”.

Lúc 9h (t₁ = 9h − 8h = $\frac{1}{2}$ h (nghỉ) = 0,5h) người đi xe đạp đi được quãng đường:  

S₁  = v₁t₁ = 12 . 0.5 = 6 (km).

Lúc 9h (t₂ = 9h − 8h = 1h) quãng đường người đi bộ đi được:

S₂ = v₂t₂ = 4 . 1 = 4 (km).

⇒ Khoảng cách giữa 2 xe lúc 9h là: 6 + 4 =10 (km).

Chọn gốc thời gian là lúc 9h, gốc tọa độ tại vị trí của người đi xe đạp, chiều dương là chiều chuyển động của xe đạp.

Ta có, phương trình tọa độ của 2 người:

+ Người đi xe đạp: x₁ = 12t

+ Người đi bộ: x₂ = 10 + 4t

Hai người gặp nhau khi: x₁ = x₂ ⇔ 12t = 10 + 4t ⇒ t =1,25h

⇒ Hai người gặp nhau lúc 9 + 1,25h = 10,25h

Vị trí hai người gặp nhau là x = 1,25 . 12 = 15 (km) (cách gốc đã chọn 15km).

Câu 34: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng. Khi đó hệ điều kiện của x, y để tính số nguyên liệu mỗi loại cần dùng là gì?

Lời giải:

Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.

Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có: 

$\left\{\begin{array}{l}0\le x\le 100\\ 0\le y\le 9\end{array}\right.$

Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B

⇒ Từ x tấn nguyên liệu loại I ta chiết xuất được: 20x (kg) chất A và 0,6y (kg) chất B.

Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10kg chất A và 1,5kg chất B

⇒ Từ y là số tấn nguyên liệu loại II  ta chiết xuất được: 10y (kg) chất A và 1,5y (kg) chất B.

Như vậy ta chiết xuất được 20x+10y (kg) chất A và 0,6x+1,5y (kg) chất B.

Khi đó ta có hệ điều kiện là:

$\left\{\begin{array}{l}0\le x\le 10\\ 0\le y\le 9\\ 20x+10y\ge 140\\ \mathrm{0,6}x+\mathrm{1,5}y\ge 9\end{array}\right.$  ⇔ $\left\{\begin{array}{l}0\le x\le 10\\ 0\le y\le 9\\ 2x+y\ge 14\\ 2x+5y\ge 30\end{array}\right.$.

Câu 35: Tính giá trị biểu thức: (7⁵ + 7⁹)(5⁴ + 5⁶)(3³ . 3 – 9²).

 

Lời giải:

(7⁵ + 7⁹)(5⁴ + 5⁶)(3³ . 3 – 9²)

= (7⁵ + 7⁹)(5⁴ + 5⁶)(3⁴ – 9²)

= (7⁵ + 7⁹)(5⁴ + 5⁶)[3⁴ –(3²)²]

= (7⁵ + 7⁹)(5⁴ + 5⁶)(3⁴ –3⁴)

= (7⁵ + 7⁹)(5⁴ + 5⁶). 0

= 0.

Câu 36: Lớp 10A chọn ra một số học sinh tham gia làm bài khảo sát học sinh giỏi môn Toán. Đề thi có 3 câu. Sau khi chấm bài giáo viên tổng kết được như sau: Có 5 học sinh làm được câu 1, có 6 học sinh làm được câu 2, có 4 học sinh làm được câu 3. Có 3 học sinh làm được câu 1 và câu 2, có 2 học sinh làm được câu 1 và câu 3, có 1 học sinh làm được câu 2 và câu 3 và chỉ có 1 học sinh làm được cả 3 câu. Hỏi có tất cả bao nhiêu học sinh tham gia làm bài khảo sát?

Lời giải:

Gọi A là tập hợp học sinh làm được câu 1⇒ n (A) = 5

Gọi B là tập hợp học sinh làm được câu 2⇒ n (B) = 6

Gọi C là tập hợp học sinh làm được câu 3⇒ n (C) = 4

3 học sinh làm được câu 1 và 2 ⇒ n (A ∩ B) = 3

2 học sinh làm được câu 1 và 3⇒ n (A ∩ C) = 2

1 học sinh làm được câu 2 và 3⇒ n (B ∩ C) = 1

1 học sinh làm được cả 3 câu ⇒ n (A ∩ B ∩ C) = 1

Vậy (A ∪ B ∪ C)là tập hợp tất cả học sinh làm bài khảo sát

⇒ n (A ∪ B ∪ C) = n (A ∪ B) + n (C) − n [(A ∪ B) ∩ C]

⇒ n (A ∪ B ∪ C) = n (A) + n (B) – n (A ∩ B) + n (C) − [n (A ∩ C) + n (B ∩ C)

−  n (A ∩ B ∩ C)

⇒ n (A ∪ B ∪ C) = n (A) + n (B) + n (C) − n( A ∩ B) – n (A ∩ C) – n (B ∩ C)

+ n (A ∩ B ∩ C)

⇒ n (A ∪ B ∪ C) = 5 + 6 + 4 – 3 – 2 – 1 + 1

⇒ n (A ∪ B ∪ C) = 10

Vậy có 10 học sinh làm bài khảo sát.

Câu 37: Phân tích thành nhân tử: 10x – 25 – x².

Lời giải:

10x – 25 – x²

= – (x² – 10x + 25)

= – (x² – 2.5x + 5²)

= – (x – 5)².

Câu 38: Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Lời giải:

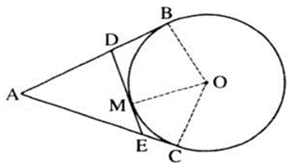
Vì AB, AC là hai tiếp tuyến của (O) lần lượt tại B và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: AB = AC

Vì DB, DM là hai tiếp tuyến của (O) lần lượt tại B và M. Theo tính chất của hai tiếp tuyến cắt nhau ta có: DB = DM

Vì EM, EC là hai tiếp tuyến của (O) lần lượt tại M và C. Theo tính chất của hai tiếp tuyến cắt nhau ta có: EM = EC

Chu vi tam giác ADE là:

AD + DE + EA

= AD + (DM + ME) + EA

= (AD + DM) + (ME + EA)

= (AD + DB) + (EC + EA) (do DB = DM, EM = EC)

= AB + AC = 2AB (do AB = AC).

Câu 39: Cho tam giác ABC có các trung tuyến BD và CE . Trên cạnh BC lấy các điểm M, N sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD , K là giao điểm của AN và CE . Chứng minh rằng:

a) BCDE là hình thang.

b) K là trung điểm của EC.

c) BC = 4IK

Lời giải:

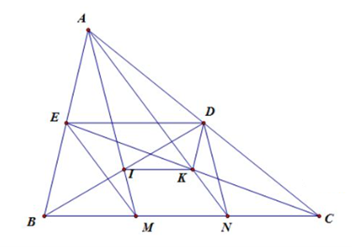
a) Vì BD và CF là trung tuyến nên ED là đường trung bình của tam giác ABC (E, D lần lượt là trung điểm AB, AC)

Suy ra: ED // BC ⇒ EDCB là hình thang

b) Trong tam giác ABN có E, M là trung điểm của AB và BN (do BM = MN = NC)

⇒ EM là đường trung bình của ∆ABN

⇒ EM // AN ⇒ EM // KN

Trong ∆EMC có N là trung điểm của CM vì MN = NC và NK // EM

⇒ K là trung điểm của CE

c) Tương tự: Trong ∆BDN có M là trung điểm BN và MI // DN

Suy ra: MI là đường trung bình của tam giác BDN

⇒ I là trung điểm BD.

Trong hình thang BEDC có IK là đoạn nối trung điểm của hai đường chéo nên:

$IK=\frac{BC-DE}{2}=\frac{2DE-DE}{2}=\frac{DE}{2}$

⇒ 2IK = DE ⇒ 4IK = 2DE = BC

Vậy 4IK = BC.

Câu 40: Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng và trục Ox bằng 45°.

Lời giải:

Vì hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0 ⇔ m ≠  $\frac{-1}{2}$.

Gọi góc α là góc tạo bởi đường thẳng và trục Ox .

Theo giả thiết α = 45°. Ta có:

tanα = a ⇒ tan45° = 2m + 1

⇔ 1 = 2m + 1 ⇔ 0 = 2m ⇔ m = 0.

Câu 41: Một người vay ngân hàng 30 000 000 (ba mươi triệu) đồng với lãi suất ngân hàng là 5% một năm và theo thể thức lãi đơn (tiền lãi không gộp vào chung với vốn). Hãy thiết lập hàm số thể hiện mối liên hệ giữa tổng số tiền nợ T (VNĐ) và số nợ (năm).

Lời giải:

Một người vay ngân hàng 30000000 VNĐ với lãi suất 5% một năm theo thể thức lãi đơn.

Sau 1 năm người này nợ thêm: 30000000 . 5% = 1500000 (VNĐ)

Sau n năm người này nợ thêm: 1500000.n (VNĐ)

Khi đó tổng số tiền người đó nợ sau n năm là: 1500000.n + 30000000 (VNĐ)

Hàm số thể hiện mối liên hệ giữa tổng số tiền nợ T (VNĐ) và số nợ n (năm) là:

T = 1500000.n + 30000000.

Câu 42: Bảng giá cước gọi quốc tế của công ty viễn thông A được cho bởi bảng sau:

Gọi T (đồng) là số tiền khách hàng phải trả khi gọi quốc tế trong t phút. Lập hàm số của T theo t.

Lời giải:

Nếu khách hàng gọi quốc tế không quá 8 phút, ta có hàm số là:

T = 6500.t (với t ≤ 8)

Nếu khách hàng gọi quốc tế trên 8 phút và không quá 15 phút, ta có hàm số là:

T = 8.6500 + (t – 8).6000 = 6000.t + 4000 (với 8 < t ≤ 15)

Nếu khách hàng gọi quốc tế trên 15 phút và không quá 25 phút, ta có hàm số là:

T= 8.6500 + (15 – 8).6000 + (t – 15).5500 = 5500.t + 11500 (với 15 < t ≤ 25)

Nếu khách hàng gọi quốc tế trên 25 phút, ta có hàm số là:

T = 8.6500 + (15 – 8).6000 + (25 – 15).5500 + (t – 25).5000 = 5000t + 24000 (với t > 25)

Câu 43: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: (x – 5)(2x + 3) – 2x(x – 3) + x + 7.

Lời giải:

(x – 5)(2x + 3) – 2x(x – 3) + x + 7

= x.(2x + 3) + (–5).(2x + 3) – 2x.(x – 3) + x + 7

= (x.2x + x.3) + (–5).2x + (–5).3 – (2x.x + 2x.(–3)) + x + 7

= 2x² + 3x – 10x – 15 – 2x² + 6x + x + 7

= (2x² – 2x²) + (3x – 10x + 6x + x) + 7 – 15

= – 8

Vậy với mọi giá trị của biến x, biểu thức luôn có giá trị bằng –8.

Câu 44: Tìm số tự nhiên n sao cho 25n + 3 chia hết cho 53.

Lời giải:

Ta có: 25n + 3 ⋮ 53

⇒ 53n + 25n + 3 ⋮ 53

⇒ 78n + 3 ⋮ 53

⇒ 78.(n – 2) + 159 ⋮ 53

⇒ n – 2 ⋮ 53

⇒ n – 2 ∈ B(53) = 53k (k ∈ ℕ)

⇒ n = 53k + 2 (k ∈ ℕ)

Vậy n có dạng 53k + 2 (k ∈ ℕ).

Câu 45: Tổng của 5 số là 600. Tìm số thứ 5, biết rằng số này bằng số trung bình cộng của bốn số còn lại.

Lời giải:

Số thứ năm bằng số trung bình cộng của bốn số còn lại nên ta coi số thứ năm bằng 1 phần thì tổng bốn số còn lại là 4 phần.

Tổng của 5 số là:

1 + 4 = 5 (phần)

Số thứ 5 là:

600 : 5 = 120.

Câu 46: Tính diện tích tam giác ABC có AB = 3; BC = 5; CA = 6.

Lời giải:

Áp dụng công thức Hê – rông: S = $\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$  trong đó p là nửa chu vi; a, b, c là độ dài các cạnh của tam giác

Nửa chu vi tam giác ABC là: (3 + 5 + 6) : 2 = 7

Diện tích tam giác ABC là:

S_ABC = $\sqrt{p\left(p-BC\right)\left(p-AC\right)\left(p-AB\right)}=\sqrt{7.\left(7-5\right).\left(7-6\right).\left(7-3\right)}=2\sqrt{14}$ .

Câu 47: Bạn An mua một số táo và lê. Biết rằng hiệu bình phương của số táo và lê bằng 41. Hỏi bạn An mua bao nhiêu quả táo (Biết rằng số táo nhiều hơn lê)?

Lời giải:

Gọi số táo và số lê mà bạn An mua lần lượt là a và b

Số táo nhiều hơn số lê nên a > b

Hiệu bình phương của số táo và số lê bằng 41 nên ta có:

a² – b² = 41

⇔ (a – b)(a + b) = 41

$\left\{\begin{array}{l}a-b=1\\ a+b=41\end{array}\right.$  ⇔ $\left\{\begin{array}{l}a=21\\ b=20\end{array}\right.$

Vậy bạn An mua 21 quả táo.

Câu 48: Rút gọn biểu thức: (x – 3)(x + 3) – (x – 3)².

Lời giải:

(x – 3)(x + 3) – (x – 3)²

= x² – 9 – (x² – 6x + 9)

= x² – 9 – x² + 6x – 9

= 6x.

Câu 49: Cho tam giác ABC, chứng minh : sin 2A + sin 2B + sin 2C = 4sinAsinBsinC.

Lời giải:

Theo tính chất tổng ba góc trong một tam giác ta có

A + B + C = π ⇒ C = π − (A + B)

⇒ sin(A+B) = sin C, cos (A+B) = − cos C

Ta có:

sin 2A + sin2B + sin2C

= 2 sin(A+B)cos(A − B) + 2 sinC cosC

= 2 sinC cos(A − B) + 2 sinC cosC

= 2 sinC[cos(A − B) + cosC]

= 2 sinC[cos(A − B) − cos(A + B)]

= 2 sinC . 2 sinA sinB

= 4 sinA sinB sinC.

Câu 50: Một khu đất hình chữ nhật có chiều dài là 127m, chiều rộng kém chiều dài 29m. Người ta đóng cọc xung quanh khu đất cứ 5m đóng 1 cọc. Tính số cọc cần để đóng.

Lời giải:

Chiều rộng khu đất hình chữ nhật là:

127 – 29 = 98 (m)

Chu vi khu đất HCN là:

(127 + 98) . 2= 650 (m)

Cần số cọc là:

650 : 5 =130 (cọc).