Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 87)

Đề bài: Cho tam giác ABC vuông tại A, M là trung điểm của BC. D, E lần lượt là hình chiếu của M trên AB và AC.

a) Tứ giác ADME là hình gì, tại sao?

b) Chứng minh DE =$\frac{1}{2}BC$ .

c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành. Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.

d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?

Lời giải:

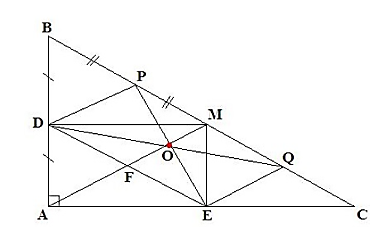
a) Ta có D, E là hình chiếu của M trên AB, AC

Nên DM ⊥ AB và ME ⊥ AC, hay $\widehat{ADM}=\widehat{AEM}=90°$

Xét tứ giác ADME có $\widehat{DAE}=\widehat{ADM}=\widehat{AEM}=90°$

Suy ra ADME là hình chữ nhật.

b) Xét ΔABC vuông tại A có M là trung điểm BC

Suy ra AM =$\frac{1}{2}BC$

Vì ADME là hình chữ nhật có AM, DE là hai đường chéo, suy ra AM = DE

Mà AM =$\frac{1}{2}BC$

Do đó DE =$\frac{1}{2}BC$ .

c) Ta có AD ⊥ AC và ME ⊥ AC, suy ra AD // ME

Mà M là trung điểm của BC

Suy ra E là trung điểm của AC

Xét tam giác AMC có E, Q lần lượt là trung điểm của AC, MC

Suy ra QE là đường trung bình

Do đó QE // AM, QE = $\frac{1}{2}AM$(1)

Ta có DM ⊥ AB và AB ⊥ AC

Suy ra DM // AC

Mà M là trung điểm của BC

Suy ra D là trung điểm của AB

Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM

Suy ra DP là đường trung bình của ΔBAM

Do đó DP // AM và DP = $\frac{1}{2}AM$ (2)

Từ (1) và (2) suy ra DP // EQ, DP = EQ

Do đó DPQE là hình bình hành.

Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)

Ta có P, Q lần lượt là trung điểm của BM, MC và M là trung điểm BC

Suy ra M là trung điểm PQ

Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ

Suy ra AM là đường trung bình của DPQE

Do đó AM đi qua trung điểm DE, gọi điểm đó là F

Từ đó AM là trục đối xứng của DPQE tức là đi qua O

Vậy tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.

d) Để hình bình hành DPQE là hình chữ nhật thì $\widehat{APQ}=\widehat{PQE}=\widehat{QED}=\widehat{EDP}=90°$

Ta xét ΔBAM nếu DP ⊥ BM thì AM ⊥ BM

Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao

Suy ra ΔABC vuông cân tại A

Vậy để hình bình hành DPQE là hình chữ nhật thì tam giác vuông ΔABC cần thêm điều kiện cân tại A.