Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 94)
Lời giải:
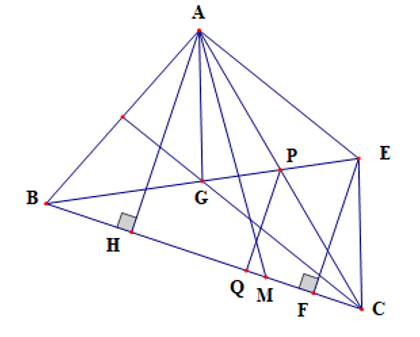
Dựng hình bình hành AGCE
Ta có:
Kẻ EF ⊥ BC (F ∈ BC)
Khi đó
Do đó đạt giá trị nhỏ nhất khi M ≡ F
Gọi P là trung điểm của AC, Q là hình chiếu vuông góc của P lên BC
Vì AGCE là hình bình hành, P là trung điểm của AC
Suy ra P là trung điểm của GE
Do đó
Vì G là trọng tâm tam giác ABC, BP là trung tuyến
Suy ra
Ta có: BE = BP + PE
Hay
Xét ∆BPQ và ∆BEF có
là góc chung;
Suy ra: ∆BPQ ∽ ∆BEF (g.g)
Do đó
Xét DAHC có P là trung điểm của AC và AH // PQ (vì cùng vuông góc với BC)
Suy ra Q là trung điểm của CH
Hay ; mà
Ta có:
Do đó:
Vậy
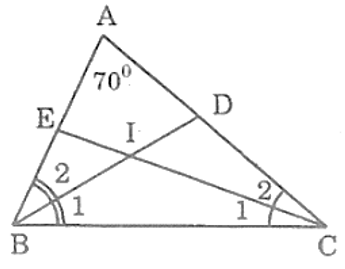
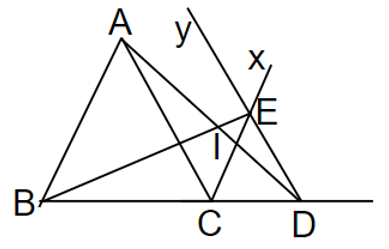
Đề bài. Cho tam giác ABC có , các đường phân giác BD, CE cắt nhau ở I. Tính
 Lời giải:
Lời giải:
Trong ∆ABC, ta có: (tổng ba góc trong tam giác)
Suy ra:
Ta có:
(vì BD là tia phân giác)
(vì CE là tia phân giác)
Trong ∆BIC, ta có:
(tổng 3 góc trong tam giác)
Suy ra:
Đề bài. Cho tam giác ABC có . Kẻ đường cao CH. Biết HB - HA = AC. Tính
Lời giải:
 Ta có: HB – HA= AC; HB + HA = AB
Ta có: HB – HA= AC; HB + HA = AB
Suy ra:
AC2 = AH.AB =
⇒
⇔
⇔
Suy ra:
Lời giải:
 Ta có:
Ta có:
Suy ra ABHK nội tiếp đường tròn đường kính AB
⇒
⇒ ΔCHK ∽ ΔCAB (g.g)
⇒
Suy ra: AB =
Mặt khác:
⇒
Do
Lời giải:
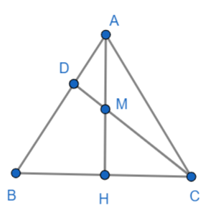
Kẻ HF // DC
Xét tam giác DBC có:
HB = HC (tam giác ABC có AH vừa là đường cao vừa là đường trung trực)
DC // HF
N là trung điểm DB (DN = NB) (1)
Xét tam giác AFH có: M là trung điểm AH (MA = MH)
DM // HF (HF // DC, M thuộc DC)
Suy ra: D là trung điểm NA hay DN = NA (2)
Từ (1), (2): DN = DA = NB
Vậy
Lời giải:
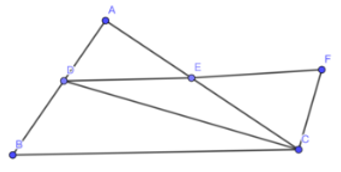
a) Xét tam giác AED và CEF có:
EA = EC
(đối đỉnh)
ED = EF
⇒ ∆AED = ∆CEF (c.g.c)
⇒ DA = CF
Mà DA = DB nên DB = CF
b) ∆AED = ∆CEF nên:
Suy ra: AB // CF
⇒ (so le trong)
Xét tam giác BDC và FCD có:
DC chung
BD = CF
⇒ ∆BDC = ∆FCD (c.g.c)
c) ∆BDC = ∆FCD nên
Suy ra: DE // BC (2 góc so le trong bằng nhau)
Lại có BC = DF = 2DE
Nên: .
Đề bài. Cho tam giác đều ABC cạnh 2a, G là trọng tâm. Khi đó độ dài bằng?
Lời giải:
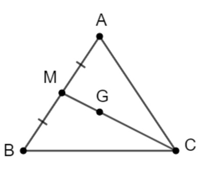
Gọi M là trung điểm AB
Lời giải:
=
G là trọng tâm nên
Ta có
Vậy
Đề bài. Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
Lời giải:
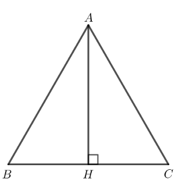
a) Do tam giác ABC đều nên và AB = BC = CA = a.
Khi đó:
b) Do AH là đường cao của tam giác ABC nên AH ⊥ BC
Suy ra:
Đề bài. Cho tam giác ABC đều cạnh a, đường cao AH. Tính độ dài
Lời giải:
AH là đường cao vừa là đường phân giác nên
Hay
Lại có:
Suy ra:
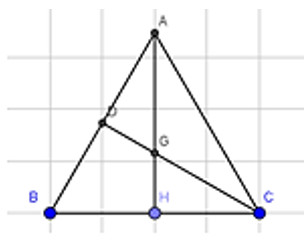
Đề bài. Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị ?
Lời giải:
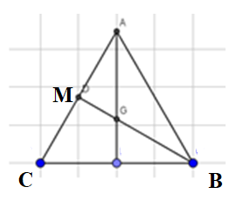
Đề bài. Cho tam giác ABC đều có cạnh bằng . Gọi M là trung điểm của AC. Tính độ dài vectơ .
Lời giải:
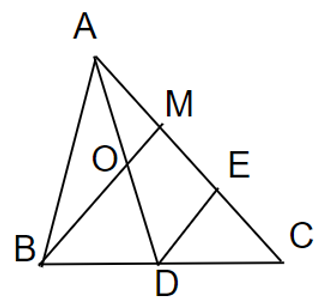
Suy ra:
1) Chứng minh tứ giác MNIK là hình bình hành.
2) Chứng minh tam giác ABC và tam giác DEF có cùng trọng tâm.
Lời giải:

Nối A vs N
a) Xét tam giác CEF có: N là trung điểm của EF (gt) và A là trung điểm của FC (vì C đối xứng với F qua A)
⇒ AN là đường trung bình của tam giác CEF
⇒ AN//CE và
⇒ (vì BC = CE)
⇒ AN = BM(vì )
Xét tứ giác ANMB có: AN = MB (cmt) và AN//MB
(vì AN// CE; B, M, C, E thẳng hàng)
⇒ tứ giác ANMB là hình bình hành
⇒ MN // AB và AB = MN (1)
xét tam gíac AGD có: I là trung điểm của AG (gt) và K là trung điểm của DG (gt)
⇒ IK là đường trung bình của tam giác AGD
⇒ và IK //AD
Mà B là trung điểm của AD (vì A đx vs D qua B)
⇒ AB = BD =
⇒ IK = AB () (2)
Từ (1), (2) ⇒ IK = MN
Ta có: MN// AB (cmt); B thuộc AD ⇒ MN//AD
Xét tứ giác MNIK có: IK = MN (cmt) và IK // MN (cùng // AD)
⇒ tứ giác MNIK là hình bình hành (đpcm)
b) Do tứ giác MNIK là hình bình hành (câu a) mà G là giao điểm của IM và KN nên G là trung điểm của IM là KN
⇒ IG = MG và KG = NG
Mặt khác: I là trung điểm của AG (gt) ⇒ IG = AI ⇒ AI = IG = GM
K là trung điểm của DG (gt) ⇒ DK = KG ⇒ DK = KG = GN
xét tam giác ABC có: AM là đường trung tuyến và AI = IG = GM (cmt)
⇒ G là trọng tâm của tam giác ABC (*)
Xét tam giác DEF có: DN là đg trung tuyến (gt) và DK = KG = GN (cmt) ⇒ G là trọng tâm của tam giác DEF (**)
Từ (*), (**) ⇒ G vừa là trọng tâm của tam giác ABC vừa là trọng tâm của tam giác DEF
⇒ Tam giác ABC và tam giác DEF có cùng trọng tâm là G (đpcm).
Lời giải:
a/ Gọi E là trung điểm của MC
Từ giả thiết: nên AM = ME = EC
Xét tam giác BCM có ME = EC (cmt); DB = DC (gt)
⇒ DE là đường trung bình của tam giác BCM
⇒ DE // BM
Xét tam giác ADE có
AM = ME (cmt)
BM // DE (cmt)
⇒ OM // DE
⇒ OA = OD (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
b/ Ta có DE là đường trung bình của tam giác BCM
⇒
Xét tam giác ADE có
OA = OD (cmt); AM=ME (cmt) ⇒ OM là đường trung bình của tam giác ADE
⇒
Đề bài. Cho tam giác ABC. Chứng minh rằng nếu thì G là trọng tâm của tam giác ABC.
Lời giải:
⇔
⇔
Từ đó suy ra ba điểm A, G, I thẳng hàng, trong đó GA = 2GI, G nằm giữa A và I.
Vậy G là trọng tâm của tam giác ABC.
Lời giải:
Ta có MA = MB ⇒ tam giác MAB cân tại M
⇒
+ MA = MC ⇒ tam giác MAC cân tại M
⇒
Trong tam giác ABC có (tổng 3 góc trong một tam giác bằng 180°)
⇒
⇒
Suy ra:
⇒ tam giác ABC vuông tại A.
Đề bài. Cho tam giác ABC nhọn (AB < AC ) có ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác AEB đồng dạng tam giác AFC.
b) Chứng minh: AF.AB = AE.AC và tam giác AEF đồng dạng với tam giác ABC.
Lời giải:
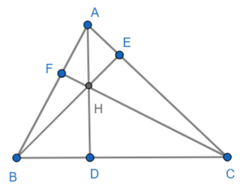
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
chung
Do đó: ΔAEB ∽ ΔAFC (g-g)
b) Ta có: ΔAEB ∽ ΔAFC(cmt)
nên hay AE.AC = AF.AB
Xét ΔAEF và ΔABC có
(cmt)
chung
Do đó: ΔAEF ∽ ΔABC (c-g-c).
Đề bài. Cho tam giác ABC nhọn (AB < AC) có các đường cao BD và CE.
a, Cho góc A = 60 độ và AC = 12cm. Tính AE.
b, Tia DE cắt BC ở F, chứng minh tam giác ADE đồng dạng với tam giác ABC.
Lời giải:
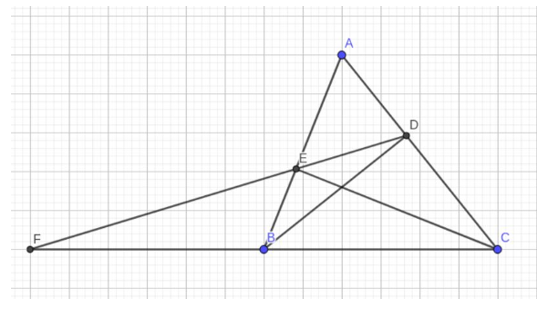 a) Ta có:
a) Ta có:
b) Xét ΔADB, ΔAEC có:
Chung
⇒ ΔADB ∽ ΔAEC(g.g)
⇒
Mà
⇒ΔADE ∽ ΔABC (c.g.c)
c.Từ câu b ⇒
⇒
Mà
⇒ ΔFBE ∽ ΔFDC (g.g)
⇒
⇒ FB.FC = FE.FD.
Đề bài. Cho tam giác ABC nhọn, đường cao AH. M, N là hình chiếu vuông góc của H lên AB và AC.
a) Biết AH = 3 cm, CH = 4 cm, tính HN và (số đo góc làm tròn đến độ).
b) Chứng minh rằng tam giác ANM đồng dạng với tam giác ABC.
Lời giải:
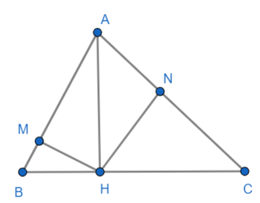 a) Áp dụng hệ thức lượng trong tam giác AHC vuông tại H:
a) Áp dụng hệ thức lượng trong tam giác AHC vuông tại H:
Suy ra:
b) Áp dụng hệ thức lượng trong các tam giác vuông AHC, AHB có:
AH2 = AN.AC; AH2 = AM.AB
Suy ra: AN.AC = AM.AB
⇒
Xét tam giác AMN và tam giác ABC có:
Chung
⇒ ∆AMN ∽ ∆ABC (c.g.c).
Đề bài. Cho tam giác ABC nhọn có đường cao AH. Gọi E là hình chiếu của H trên AB.
a. Biết AE = 3,6 cm; BE = 6,4 cm. Tính AH, EH và góc (Số đo góc làm tròn đến độ)
b. Kẻ HF vuông góc với AC tại F. Chứng minh AB.AE = AC.AF.
c. Đường thẳng qua A và vuông góc với EF cắt BC tại D; EF cắt AH tại O.
Chứng minh rằng
Lời giải:
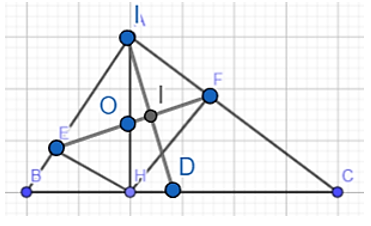 a) Trong tam giác ABH vuông tại H, ta có:
a) Trong tam giác ABH vuông tại H, ta có:
EH2 = AE.BE = 3,6.6,4 = 23,04 ⇒ EH = 4,8 (cm)
AH2 = AE.AB = 3,6(3,6 + 6,4) = 36 ⇒ AH = 6 (cm)
b) Áp dụng hệ thức lượng trong tam giác ABH vuông tại H:
AH2 = AE.AB
Áp dụng hệ thức lượng trong tam giác ACH vuông tại H:
AH2 = AF.AC
Suy ra: AB.AE = AC.AF (= AH2)
c) Xét tam giác AEF và tam giác ABC có:
Chung
(từ AB.AE = AC.AF)
⇒ ∆AEF ∽ ∆ACB (c.g.c)
⇒
Gọi I là giao điểm AD và EF
Có: tam giác IAF vuông tại I nên
Tam giác ABH vuông tại H nên
Mà: hay nên
Xét tam giác AOE và ADC có:
Suy ra: ∆AOE ∽ ∆ADC (g.g)
⇒
(vì tam giác ABH vuông tại H nên ).
Lời giải:
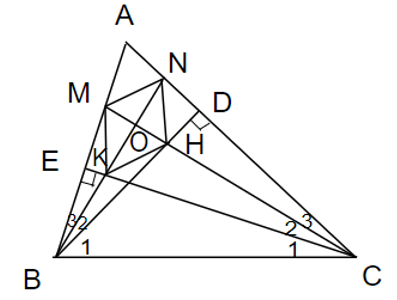 a) Vì tam giác BEC vuông ở E
a) Vì tam giác BEC vuông ở E
⇒ ( phụ nhau)
Mà ( BN là phân giác góc ABD)
⇒
Vì tam giác DBC vuông ở D ⇒ (phụ nhau)
Mà CM là tia phân giác góc ACE)
⇒
Lấy (1) + (2) ta được:
⇔
⇔
Xét tam giác OBC có:
⇒
⇒ OB ⊥ OC
⇒ BN ⊥ CM
b) Vì BN ⊥ CM (cmt)
⇒ MH ⊥ KN
Xét tứ giác MNHK có 2 đường chéo MH và KN vuông góc với nhau
⇒ MNHK là hình thoi.
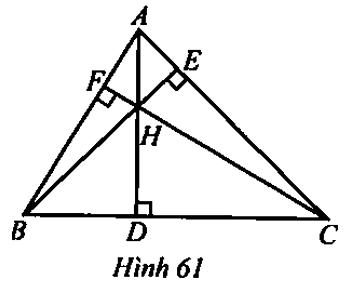
Lời giải:
• Xét tam giác HAB có BD ⊥ AH, AE ⊥ BH, HF ⊥ AB và ba đường cao BD, AE, HF cắt nhau tại C.
Do đó C là trực tâm tam giác HAB.
• Xét tam giác HBC có HD ⊥ BC, BF ⊥ HC, CE ⊥ BH và ba đường cao HD, BF, CE cắt nhau tại A.
Do đó A là trực tâm tam giác HBC.
• Xét tam giác HCA có HE ⊥ AC, AF ⊥ HC, CD ⊥ AH và ba đường cao HE, AF, CD cắt nhau tại B.
Do đó B là trực tâm tam giác HCA.
Vậy trực tâm của các tam giác HAB, HBC, HCA tương ứng là C, A, B.
Đề bài. Cho tam giác ABC có 3 góc nhọn và các trung tuyến BM và CN vuông góc với nhau. Chứng minh:
Lời giải:
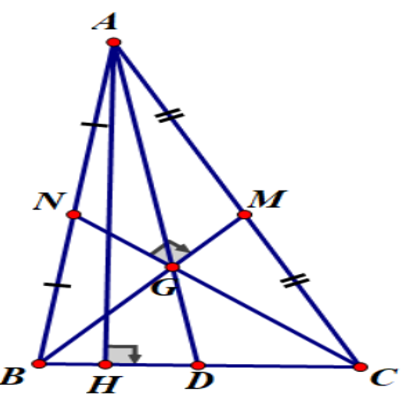 Kẻ đường cao AH, trung tuyến AD, trọng tâm G
Kẻ đường cao AH, trung tuyến AD, trọng tâm G
Tam giác AHD vuông tại H nên AH ≤ AD
⇒
Ta có: (2)
Mà BM vuông góc CN nên GD là trung tuyến ứng với cạnh huyền BC
Suy ra: BC = 2GD (3)
Mà G là trọng tâm nên 3GD = AD (4)
Từ (1), (2), (3), (4) ⇒
Lời giải:
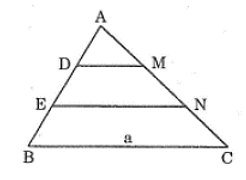 Ta có:
Ta có:
Suy ra: AE = AD + DE =
Trong ΔABC, ta có: DM // BC (gt)
Nên: (hệ quả định lí Ta-lét)
Suy ra:
Từ (1) và (3) suy ra:
Suy ra:
Trong ΔABC, ta có: EN // BC (gt)
⇒
⇒
Lời giải:
 a) Có AB // Cx (gỉa thiết)
a) Có AB // Cx (gỉa thiết)
⇒ (2 góc đồng vị)
Mà (vì tam giác ABC đều)
⇒
Có AC // Dy (gỉa thiết) ⇒ (2 góc đồng vị)
Có
⇒ Tam giác ECD đều
b) (kề bù)
(kề bù)
⇒
Xét tam giác ACD và tam giác BCE
CD = ED (tam giác ECD đều)
(cmt)
AC = BC (tam giác ABC đều)
⇒ ∆ACD = ∆BCE (c.g.c)
⇒ AD = BE (2 cạnh tương ứng).
b) Lấy E đối xứng Dqua M. Chứng minh rằng AE//MN.
c) D nằm ở vị trí nào trên cạnh BC để ANDM là hình chữ nhật.
Lời giải:
 a) Xét tứ giác ANDM có 3 góc vuông tại A, M, N
a) Xét tứ giác ANDM có 3 góc vuông tại A, M, N
⇒ ANDM là hình chữ nhật
Vậy ANDM là hình chữ nhật
b) Vì ANDM là hình chữ nhật
⇒ AN = DM; AN//DM
Lại có E đối xứng với D qua M
⇒ DM = ME
⇒ ME // AN; ME = AN
⇒ ANME là hình bình hành
⇒ AE // MN
Vậy AE // MN
c) D nằm ở vị trí nào thì ANDM đều là hình chữ nhật.
Đề bài. Cho tam giác ABC vuông cân tại A và điểm M thuộc cạnh BC. Chứng minh MB2 + MC2 = 2MA2.
Lời giải:
 Từ M kẻ ME vuông góc với AB, MF vuông góc với AC.
Từ M kẻ ME vuông góc với AB, MF vuông góc với AC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM, FMC, AEF ta có:
BM2 = EM2 + BE2 = 2.ME2 ; MC2 = 2.FM2
⇒ BM2 + MC2 = 2.(ME2 + MF2) (1)
Mà AM2 = EF2 = ME2 + MF2 (2)
Từ (1),(2) ta được MB2 + MC2 = 2MA2.
Đề bài. Cho tam giác ABC vuông cân tại A. Biết AB = AC = 4cm.
b, Từ A kẻ AD vuông góc BC tại D. Chứng minh D là trung điểm BC.
c, Từ D kẻ DE vuông góc AC tại E. Chứng minh tam giác AED vuông cân.
Lời giải:
 a) Ta có tam giác ABC vuông cân tại A nên: BC2 = AB2 + AC2 = 42 + 42 = 32
a) Ta có tam giác ABC vuông cân tại A nên: BC2 = AB2 + AC2 = 42 + 42 = 32
⇒ BC =
b) Ta có: tam giác ABC vuông cân tại A nên
Vì AD vuông góc với BC nên
⇒
Suy ra: tam giác ABD và tam giác DAC vuông cân tại D
Suy ra: DA = DB; DA = DC
⇒ DB = DC hay D là trung điểm BC.
c) Có: DE ⊥ AB nên
mà tam giác ADB vuông cân tại D nên:
⇒ Tam giác ADE vuông cân tại E.
d) Từ câu b có DA = DB = DC
Mà D là trung điểm BC nên
Vậy
a) Chứng minh DC vuông góc với BC.
b) Gọi I là giao điểm EF và BC. Chứng minh
Lời giải:
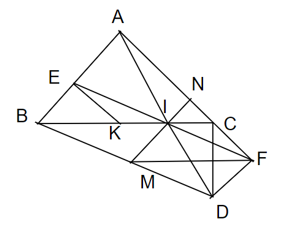
a) Ta có
BE = DF (cạnh đối hình bình hành)
BE = CF (gt)
⇒ CF=DF ⇒ tam giác CDF cân tại F
Ta có DF//BE ⇒ DF//AB mà AB ⊥ AC ⇒ DF ⊥ AC
⇒ tam giác CDF vuông cân tại F ⇒
Tam giác ABC vuông cân tại A ⇒
⇒
⇒ DC ⊥ BC (đpcm)
b/ Từ E dựng đường thẳng vuông góc với AB cắt BC tại K
Xét tam giác vuông BEK có:
⇒
⇒ tam giác BEK cân tại E ⇒ BE=KE
Mà BE = CF (gt)
⇒ KE = CF (1)
Ta có: KE ⊥ AB
AC⊥AB
⇒ CF ⊥ AB
⇒ KE // CF (2)
Từ (1) và (2) ⇒ CEKF là hình bình hành
⇒ IE = IF (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét tam giác vuông AEF có: IE = IF (cmt)
⇒
Mà EF = DB nên
Lời giải:
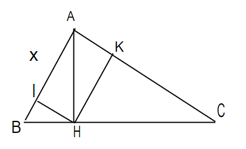 Đặt AB = x
Đặt AB = x
Dễ chứng minh tam giác HBA và tam giác ABC đồng dạng (g.g)
⇒ AB2 =BH.BC
⇒ x2 = 4BH
Hay BH =
Lại có: AB2= BH2+ AH2
⇒ AH2 =
Suy ra:
Dấu “=” khi x2 = 16 – x2 hay x = AB = ; HI = HK thì tam giác ABC vuông cân tại A.
a, Chứng minh tứ giác ADHE là hình chữ nhật và 3 điểm D, O, E thẳng hàng.
c, Cho AB = 8cm, AC = 9cm. Tính diện tích tứ giác MDEN.
Lời giải:
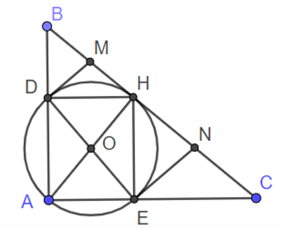 a) Do D, E thuộc đường tròn đường kính DE nên
a) Do D, E thuộc đường tròn đường kính DE nên
Xét tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Do ADHE là hình chữ nhật nên hai đường chéo DE và AH cắt nhau tại trung điểm mỗi đường. Mà O là trung điểm AH nên O là trung điểm DE.
Vậy D, O, E thẳng hàng.
b) Do AH vuông góc BC nên BC cũng là tiếp tuyến tại H của đường tròn (O)
Áp dụng tính chất hai tiếp tuyến cắt nhau, ta có : DM = MH.
Xét tam giác vuông ADH có DM = MH nên DM = MH = MB hay M là trung điểm BH.
Tương tự N là trung điểm HC.
c) Dễ thấy MDEN là hình thang vuông.
Vậy thì
Đề bài. Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD⊥BC (D∈ BC).
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ΔABC = ΔDBE
d) Chứng minh ba điểm B, M, N thẳng hàng.
Lời giải:
 a) Xét 2 tam giác vuông ΔABM và ΔDBM có:
a) Xét 2 tam giác vuông ΔABM và ΔDBM có:
BM chung
(do BM là phân giác)
⇒ΔABM = ΔDBM (cạnh huyền- góc nhọn)
⇒ BA = BD (hai cạnh tương ứng)
b) Xét 2 tam giác vuông ΔABC và ΔDBE có:
BA = BD (chứng minh ở câu a)
chung
⇒ ΔABC = ΔDBE (cạnh góc vuông- góc nhọn)
c) Xét 2 tam giác vuông ΔAMK và ΔDMH có:
AM = DM (hai cạnh tương ứng do ΔABM = ΔDBM)
(đối đỉnh)
⇒ ΔAMK = ΔDMH (cạnh huyền-góc nhọn)
⇒ MK = MH (hai cạnh tương ứng)
Xét 2 tam giác vuông ΔMNK và ΔMNH có:
MK = MH (cmt)
MN chung
⇒ ΔMNK = ΔMNH (c.g.c)
⇒ (hai góc tương ứng)
⇒ NM là tia phân giác của (đpcm) (1)
d) Do AK = DH (hai cạnh tương ứng ΔAMK = ΔDMH)
KN = HN (hai cạnh tương ứng ΔMNK = ΔMNH)
⇒ AN = AK + KN = DH + HN = DN
Xét ΔABN và ΔDBN có:
AB = DB (cmt)
BN chung
AN = DN
⇒ΔABN = ΔDBN (c.c.c)
⇒ (hai góc tương ứng)
⇒ NB là tia phân giác (2)
Từ (1) và (2) suy ra B, M, N thẳng hàng.
Đề bài. Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH. Gọi AD là phân giác của
a) Tính cạnh AH, AC biết HB = 18cm, HC = 8cm.
b) Chứng minh tam giác ADC cân và HD.BC = BD.DC.
c) Gọi E, F lần lượt là hình chiếu của H trên AB và AC.
Chứng minh SAEF = SABC.(1 - cos2B).sin2C.
Lời giải:
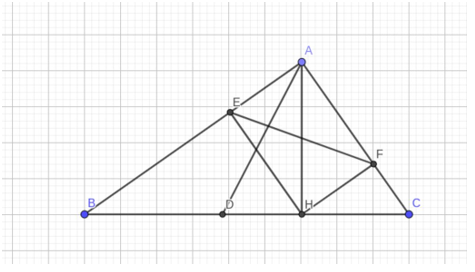 a) Ta có tam giác ABC vuông tại A, AH ⊥ BC
a) Ta có tam giác ABC vuông tại A, AH ⊥ BC
Nên: AH2 = BH.CH = 18.8 = 144
⇒ AH = 12cm.
AC =
b) Vì AD là phân giác
⇒
Suy ra: tam giác CAD cân tại C ⇒ CA = CD
Vì AD là phân giác ⇒
⇒ HD.BC = BD.AC = DB.CD
c) Ta có: HE ⊥ AB, HF ⊥ AC, AB ⊥ AC
Nên AEHF là hình chữ nhật
⇒ AH = EF
⇒
Mà
⇒ ∆AFE ∽ ∆ABC (g.g)
⇒
Ta có: 1 – cos2B = sin2B
⇒ (1 – cos2B)sin2C = sin2Bsin2C = (sinBsinC)2
=
⇒
⇒ SAEF = SABC.(1 - cos2B).sin2C.
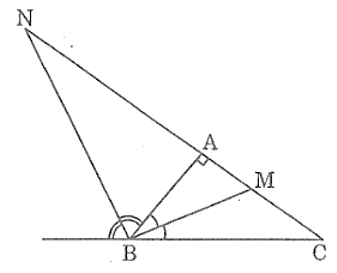 Lời giải:
Lời giải:
Vì BM là đường phân giác của góc B nên ta có:
Suy ra:
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: BM ⊥ BN
Suy ra tam giác BMN vuông tại B
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
AB2 = AM.AN
Suy ra: AN
b) Đường vuông góc với BI tại I cắt BC tại M. Chứng minh: BM = MC.
Lời giải:
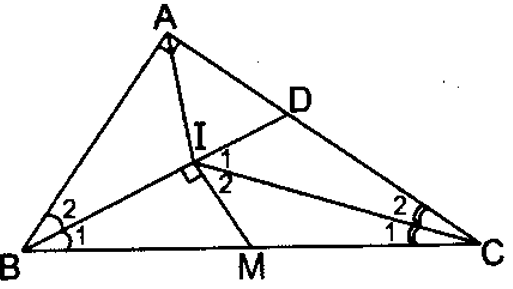 a) Gọi D là giao điểm của BI và AC
a) Gọi D là giao điểm của BI và AC
BC =
Suy ra: AD = mà AD + DC = AC = 8cm
Ta tính được: AD = 3cm, CD = 5cm
Do đó: BD2 = AB2 + AD2 = 45 nên BD =
Ta có:
Suy ra: BI = 2ID mà BI + ID = BD =
Suy ra: BI =
b)
Xét tam giác ICM và tam giác ICD có:
(vì CI là phân giác)
Chung IC
⇒ ∆ICM = ∆ICD (g.c.g)
Suy ra: CM = CD = 5cm
Ta thấy:
Mà
Suy ra M là trung điểm BC, tức BM = MC.
Đề bài. Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho . Tính tỉ số
Lời giải:
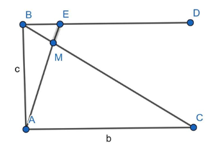 Kẻ BD// AC, AM cắt BD tại E.
Kẻ BD// AC, AM cắt BD tại E.
Xét ΔEAB có: EB = AB . tan30° =
Do BD // AC hay BE // AC nên
Đề bài. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC:
a) Chứng minh: AB2 + CH2 = AC2 + BH2.
b) Trên AB lấy E, trên AC lấy điểm F. Chứng minh: EF < BC.
c) Biết AB = 6cm; AC = 8cm. Tính AH, BH, CH.
Lời giải:
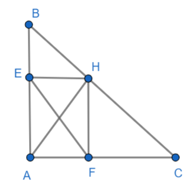 a) Áp dụng định lý Pytago vào tam giác AHB, AHC vuông có:
a) Áp dụng định lý Pytago vào tam giác AHB, AHC vuông có:
AB2 = BH2 + AH2 ⇒ AH2 = AB2 – BH2
AH2 = AC2 – CH2
Suy ra: AB2 – BH2 = AC2 – CH2
Hay AB2 + CH2 = AC2 + BH2
b) Ta có: EF2 = AE2 + AF2
BC2 = AB2 + AC2
AE < AB, AF < AC
Suy ra: EF2 < BC2
⇒ EF < BC.
c)
Mà AH2 = AC2 – CH2
Nên: CH =
BH = BC – CH = 10 – 6,4 = 3,6(cm).
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA = NB, PA = PC và tứ giác BMPN là hình bình hành.
Lời giải:
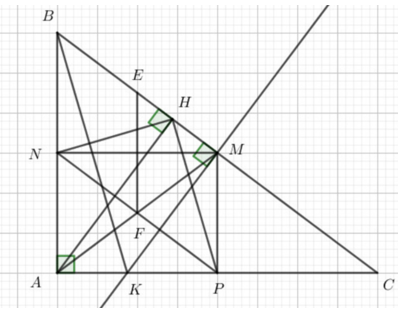 a/ MP ⊥ AC; NA ⊥ AC ⇒ MP // NA
a/ MP ⊥ AC; NA ⊥ AC ⇒ MP // NA
MN ⊥ AB; PA ⊥ AB ⇒ MN // PA
⇒ ANMP là hình bình hành
Ta có:
⇒ ANMP là hình chữ nhật
b/ MN // PA (cmt) ⇒ MN // AC
MB = MC (gt)
⇒ NA = NB
Chứng minh tương tự cũng có PA = PC
Ta có: MP//NA (cmt) ⇒ MP//NB
NA = NB; PA = PC
⇒ NP là đường trung bình của tam giác ABC
⇒ NP // BC ⇒ NP // MB
⇒ BMPN là hình bình hành
c/ Xét hình chữ nhật ANMP có
FM = FA
EM = EB (gt)
⇒ EF là đường trung bình của tam giác MAB
⇒ EF // AB
⇒ ABEF là hình thang
Ta có: MB = MC
⇒
Ta có:
⇒ FA = EB
⇒ ABEF là hình thang cân.
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Lời giải:
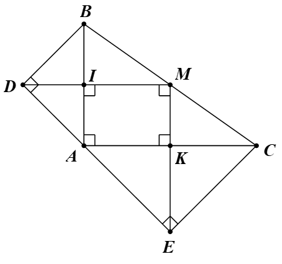 a) Ta có tam giác ADB vuông cân tại D.
a) Ta có tam giác ADB vuông cân tại D.
Suy ra
Chứng minh tương tự, ta được
Ta có
Vậy ba điểm D, A, E thẳng hàng.
b) Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra MA = MB = MC.
Do đó M nằm trên đường trung trực của đoạn AB (1)
Chứng minh tương tự, ta được D nằm trên đường trung trực của đoạn AB (2)
Từ (1), (2), suy ra DM là đường trung trực của đoạn AB.
Mà DM cắt AB tại I.
Do đó DM ⊥ AB tại I.
Chứng minh tương tự, ta được ME ⊥ AC tại K.
Tứ giác IAKM, có:
Vậy tứ giác IAKM là hình chữ nhật.
c) Tam giác ADB vuông cân tại D có DI là đường cao.
Suy ra DI cũng là đường phân giác của tam giác ADB.
Do đó
Mà (do tứ giác IAKM là hình chữ nhật).
Vậy tam giác DME là tam giác vuông cân tại M.
Đề bài. Tam giác ABC vuông tại A có AB = 21cm, góc C = 40°. Hãy tính các độ dài phân giác BD.
Lời giải:
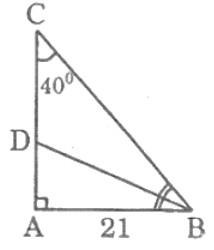 Vì tam giác ABC vuông tại A nên:
Vì tam giác ABC vuông tại A nên:
Suy ra:
Vì BD là phân giác của nên:
Trong tam giác vuông ABD, ta có:
Đề bài. Cho tam giác ABC vuông tại A, biết AB = 6cm, . Hãy giải tam giác ABC.
Lời giải:
 Ta có:
Ta có:
Đề bài. Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Hãy giải tam giác ABC.
Lời giải:
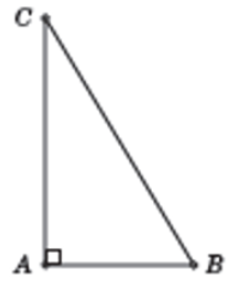 Ta có:
Ta có:
Suy ra:
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Lời giải:
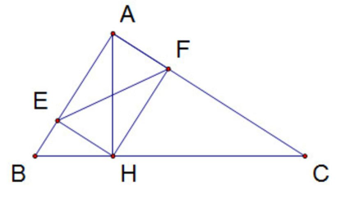 a) Xét △AHB và △CAB có:
a) Xét △AHB và △CAB có:
chung
Do đó △AHB ∽ △CAB (g.g)
⇒
Ta lại có:
AB2 = HB.BC (hệ thức lượng)
⇒ BC = 152 : 9 = 25(cm)
⇒ HC = BC – HB = 25 – 9 = 16 cm
b) Xét tứ giác AEHF có:
Do đó AEHF là hình chữ nhật
⇒ EF = AH
Ta lại có: AB.AC = AH.BC = 2SABC nên AB.AC = EF.BC.
Đề bài. Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm. AH là đường cao.
b) Tính các góc B và C của tam giác ABC.
c) Gọi M là trung điểm của BC tính diện tích tam giác AHM.
Lời giải:
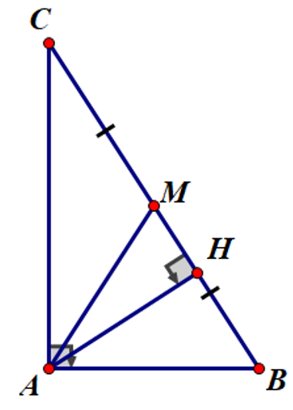 a)
a)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
AC2 = CH.BC ⇒
AH2 = BH.HC ⇒
b)
Suy ra:
c) Vì AM là đường trung tuyến ứng với BC nên AM =BM =
MH = MB – HB =
Đề bài. Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 4 cm, CH = 9cm.
b) Gọi M là trung điểm của AC. Tính góc
Lời giải:
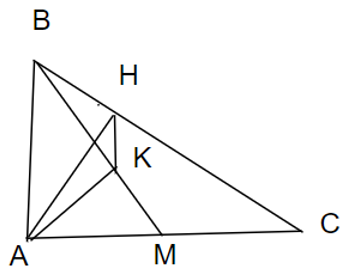 a) ΔABC vuông A có đường cao AH
a) ΔABC vuông A có đường cao AH
⇒ AH2 = BH.CH = 4.9 ⇒ AH = 6cm
BC = BH + CH = 4 + 9 = 13cm
AB2 = BH.BC = 4.13⇒
AC2 = CH.BC = 9.13⇒
b) M là trung điểm của AC
⇒ AM = MC =
ΔABC ⊥ A ⇒ AB ⊥ AC ⇒ AB⊥ AM
⇒ ΔABM ⊥ A
⇒
Mà (kề bù)
⇒
a) Ba điểm D, A, E thẳng hàng;
b) DE tiếp xúc với đường tròn có đường kính BC.
Lời giải:
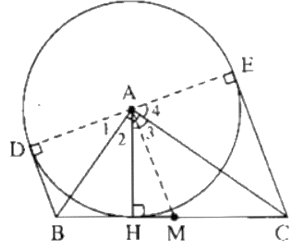 a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB là tia phân giác của góc HAD
Suy ra:
AC là tia phân giác của góc HAE
Suy ra:
Ta có:
Vậy ba điểm D, A, E thẳng hàng.
b) Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có:
AD ⊥ BD; AE ⊥ CE
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: MA//BD ⇒ MA ⊥ DE
Trong tam giác vuông ABC ta có: MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC.
Lời giải:
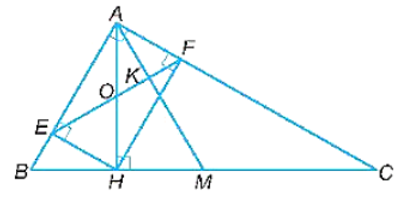 a) Vì tam giác ABC vuông tại A nên
a) Vì tam giác ABC vuông tại A nên
Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.
Do đó,
Xét tứ giác AFHE có:
Do đó, tứ giác AFHE là hình chữ nhật.
Suy ra AH = FE (hai đường chéo bằng nhau).
b) Vì tứ giác AFHE là hình chữ nhật nên
Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên
Tam giác AMB có AM = MB nên tam giác AMB cân tại M.
Do đó,
Lại có
Nên (1).
Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.
Do đó, OH = OE = OF = OA.
Tam giác OAE có OA = OE nên tam giác OAE cân tại O.
Suy ra
Mà AE song song với FH (do AFHE là hình chữ nhật) nên (hai góc so le trong).
Do đó, (2).
Lại có (3).
Từ (1), (2), (3) ta có:
Gọi K là giao điểm của AM và EF.
Khi đó,
Suy ra
Vậy AM vuông góc với EF tại K.
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 20cm. Tính AC, BH, CH, AH?
Lời giải:
 Áp dụng định lý Pytago:
Áp dụng định lý Pytago:
Lại có: AB.AC = AH.BC
⇒
AB2 = BH.BC ⇒
HC = BC – BH = 20 – 7,2 = 12,8 (cm).
Đề bài. Cho tam giác ABC vuông ở A, đường cao AH. Biết AH = 6cm và BC = 13cm. Tính AB, AC.
Lời giải:
 Ta có: AH2 = BH.CH = 62 = 36 (1)
Ta có: AH2 = BH.CH = 62 = 36 (1)
BH + HC = BC = 13(cm) (2)
Thế (2) vào (1) ta có: (13 – HC).HC = 36
⇔ 13HC – HC2 – 36 = 0
⇔
Nếu HC = 9cm thì BH = 4cm
AB2 = BH.BC ⇒
AC =
Nếu HC = 4cm thì BH = 9cm
AB2 = BH.BC ⇒
AC =
b) N là trung điểm AB, MN cắt AH tại D. Chứng minh EF // BD.
Lời giải:
a) Xét tứ giác AEHF có góc
nên AEHF là hình chữ nhật
Suy ra:
Ta có: ΔABC vuông tại A
Mà AM là trung tuyến
Nên MA = MB = MC
⇒ ΔMAC cân tại M
⇒
⇒ AM vuông góc với EF(1)
b) Xét ΔABC có M, N lần lượt la trung điểm của BC và BA nên MN là đường trung bình
⇒ MN // AC
Hay MN vuông góc với AB
Xét ΔMAB có AH, MN là các đường cao
AH cắt MN tại D
Do đó: D là trực tâm của tam giác MAB
⇒ BD vuông góc với AM (2)
Từ (1) và (2) suy ra BD // EF.
Lời giải:
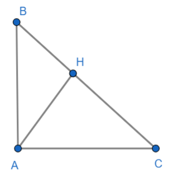
 a) Xét ΔOAB và ΔODC ta có:
a) Xét ΔOAB và ΔODC ta có:
AO = OD
BO = OC
⇒ ΔOAB = ΔODC (c−g−c)
b) Theo phần a suy ra:
Ta lại có:
Suy ra:
Xét ΔACP và ΔCAB
AC chung
AB = CD
⇒ ΔACP = ΔCAB (c.g.c)
⇒ BC = AP = 2OA.
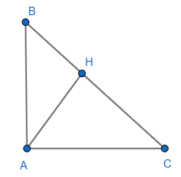
Đề bài. Cho tam giác ABC vuông tại A biết , có AH là đường cao AH = 6cm. Tính các cạnh của tam giác?
Lời giải:
 Giả sử AB = 2x thì AC = 3x
Giả sử AB = 2x thì AC = 3x
Áp dụng định lý Pytago: BC2 = AB2 + AC2 = 4x2 + 9x2
BC =
Có AH.BC = AB.AC
⇒
⇔
⇔
⇔
Suy ra:
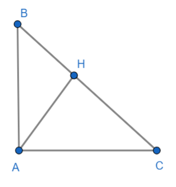
Đề bài. Cho tam giác ABC vuông tại A có AH là đường cao AH = 6cm, BC = 12,5 cm. Tính HB, HC.
Lời giải:
 Đặt HB = a (cm)
Đặt HB = a (cm)
⇒ HC = BC – HB = 12,5 – a (cm)
Xét ΔABC vuông tại A có đường cao AH vuông góc với BC ta có:
AH2 = HB.HC
⇒ a(12,5 – a) = 62 = 36
⇔ a2 – 12,5a + 36 = 0
⇔
Với a = HB = 8 cm thì HC = 12,5 – 8 = 4,5 (cm)
Với a = HB = 4,5 cm thì HC = 12,5 – 4,5 = 8 (cm).
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, CH = 12cm. Tính AH?
Lời giải:
 Áp dụng hệ thức lượng trong tam giác vuông ta có:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
BH.HC = AH2
Suy ra: AH =
Lời giải:
 Ta có: AB2 = BH.BC = 10.3,6
Ta có: AB2 = BH.BC = 10.3,6
Suy ra: AB = 6(cm)
AC =
Áp dụng định lý Pytago vào tam giác ABH vuông tại H có:
AB2 = BH2 + AH2
⇒
HM = BM – BH = 5 – 3,6 = 1,4 (cm)
Lại có:
Suy ra:
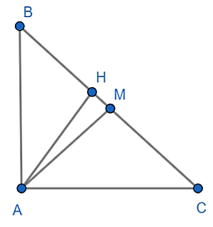
Đề bài. Cho hai tam giác ABC và A’B’C’ có cùng trọng tâm là G.
Lời giải:
Ta có:
Đề bài. Cho tam giác ABC có BA = 8, AC = 9. BC = 10. Một điểm M nằm trên BC sao cho BM = 7. Tính AM.
Lời giải:
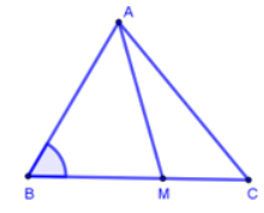 Ta có:
Ta có:
Áp dụng định lí cô-sin cho tam giác ABM ta có:
AM2 = AB2 + BM2 – AB.BM.cosB =
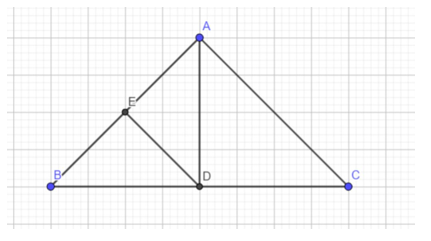
Lời giải:
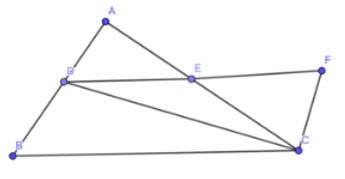 a) Xét tam giác AED và CEF có:
a) Xét tam giác AED và CEF có:
EA = EC
(đối đỉnh)
ED = EF
⇒ ∆AED = ∆CEF (c.g.c)
⇒ DA = CF
Mà DA = DB nên DB = CF
b) ∆AED = ∆CEF nên:
Suy ra: AB // CF
⇒ (so le trong)
Xét tam giác BDC và FCD có:
DC chung
BD = CF
⇒ ∆BDC = ∆FCD (c.g.c)
c) ∆BDC = ∆FCD nên
Suy ra: DE // BC (2 góc so le trong bằng nhau)
Lại có BC = DF = 2DE
Nên:
Lời giải:
Chọn D
Ta có:
⇔
⇔
⇔
⇔
Vì E là trung điểm BC nên
Xét:
.
Lời giải:
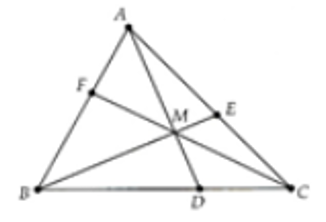 Từ bài
Từ bài
Chứng minh tương tự được:
⇒
⇒
⇒
Đề bài. Cho ΔABC, góc ngoài đỉnh C có số đo bằng 100°,
b, 2 tia phân giác Ax và By của các góc A, B cắt nhau tại O, tính góc .
Lời giải:
 a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra: .
b) Vì Ax là tia phân giác nên
Vì By là tia phân giác nên
Xét tam giác AOB có:
Suy ra: .
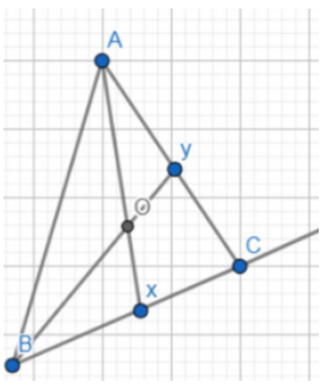
Đề bài. Cho tam giác ABC. Tìm điển N sao cho .
Lời giải:
Gọi H là trung điểm AC khi đó
Suy ra:
Giả sử P là điểm thỏa mãn
Khi đó:
Suy ra:
Mà
Nên:
Gọi Q là điểm nằm trên cạnh AB sao cho
⇒
Do đó tứ giác AQPN là hình bình hành.
Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn và P thỏa mãn H là trung điểm của AC).
Lời giải:
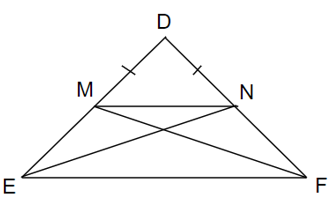 Ta có △DEF cân tại D
Ta có △DEF cân tại D
⇒ DE = DF
Xét △DNE và △DMF ta có:
DE = DF (gt)
góc chung
DM = DN (gt)
⇒ △DNE = △DMF (c.g.c)
⇒ EN = FM
Suy ra: MNFE là hình thang cân (dấu hiệu nhận biết hình thang cân).
Đề bài. Cho tam giác ABC đều cạnh a, điểm M là trung điểm BC.
Lời giải:
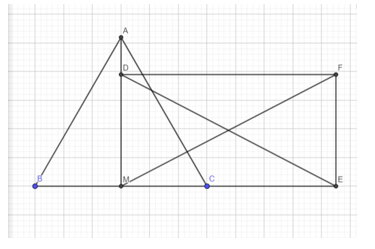 Ta có tam giác ABC đều, M là trung điểm BC nên AM vuông góc BC
Ta có tam giác ABC đều, M là trung điểm BC nên AM vuông góc BC
Suy ra:
Trên MA lấy điểm D sao cho
Trên MC lấy E sao cho ME = 2,5MB =
⇒
Vẽ hình chữ nhật MEFD nên MF = DE =
Lại có:
⇒ .
Đề bài. Cho tam giác ABC đều cạnh a, tính .
Lời giải:
Vì tam giác ABC đều nên: .
Đề bài. Cho tam giác MNP vuông tại M, đường cao MH, có MN = 6cm, NP = 10cm. Tính MP, MH, NH.
Lời giải:
 Áp dụng định lý Pytago:
Áp dụng định lý Pytago:
Lại có: MH.NP = MN.MP
⇒
.
Lời giải:
 M, N lần lượt là trung điểm AB, AC nên MN là đường trung bình của tam giác ABC ứng với cạnh BC
M, N lần lượt là trung điểm AB, AC nên MN là đường trung bình của tam giác ABC ứng với cạnh BC
⇒MN // BC hay MN // HP
⇒ MNPH là hình thang (∗)
Mặt khác:
Tam giác vuông ABH có HM là đường trung tuyến ứng với cạnh huyền nên (bổ đề quen thuộc)
⇒ Tam giác MHB cân tại M.
⇒
Mà (hai góc đồng vị với NP // AB)
⇒
⇒
Hay (**)
Từ (∗); (∗∗) ⇒ MNPH là hình thang cân (đpcm).
Đề bài. Cho tam giác ABC có và c = 12. Tính độ dài các cạnh còn lại của tam giác.
Lời giải:
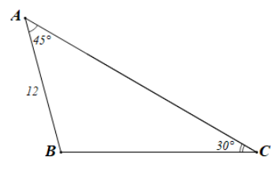 Xét tam giác ABC có:
Xét tam giác ABC có:
Suy ra:
Áp dụng định lý sin ta có:
Suy ra:
Lời giải:
Gọi tam giác thỏa mãn đề bài là ABC với (cạnh lớn nhất là BC)
Theo bài cho tam giác ABC vuông nên suy ra:
Ta có:
Mà:
Suy ra:
Diện tích tam giác là:
Đề bài. Cho . Tính sinα, cosα, cot α?
Lời giải:
Mà sin2α + cos2α = 1
⇔ sin2α + (3sinα)2 = 1
⇔ 10sin2α = 1
⇔ sin2α =
Vì α là góc nhọn nên sinα > 0, suy ra:
.
Lời giải:
.
Đề bài. Cho tan x + cot x = 4. Tính sin x, cos x, tan x, cot x.
Lời giải:
tan x + cot x = 4
⇒
⇔ tan2x – 4tanx + 1 = 0
⇔
Nếu x = 75° thì sinx =
Nếu x = 15° thì sinx = .
Đề bài. Cho tanα + cotα = m. Tìm m để tan2α + cot2α = 7.
Lời giải:
Theo giả thiết tan2α + cot2α = 7.
Nên (tanα + cotα) 2 = tan2α + cot2α + 2tanα.cotα = 7 + 2 = 9
Suy ra: tanα + cotα = 3 hoặc tanα + cotα = -3
Suy ra: m = 3 hoặc m = -3.
Lời giải:
Giả sử A ∩ B = ∅ thì ta có:
Khi đó A ∩ B ≠ ∅ thì -3 ≤ a ≤ 8
Hay a ∈ {-3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7}.
Vậy có tất cả 11 giá trị nguyên của a.
Lời giải:
Số các số thỏa mãn đề bài là .
Đề bài. Cho A = {2; 5}, B = {5; x}, C = {2; y}. Tìm x, y để A = B = C.
Lời giải:
Ta có A = {2; 5} và B = {5; x}
Để A = B thì x = 2.
Ta lại có A = {2; 5} và C = {2; y}
Để A = C thì y = 5.
Vậy x = 2, y = 5 thì A = B = C.
Lời giải:
Với p = 3, ta có:
⦁ 8p – 1 = 23 là số nguyên tố;
⦁ 8p + 1 = 25 không phải là số nguyên tố.
Với p ≠ 3, ta có: p không chia hết cho 3 nên 8p không chia hết cho 3.
Ta có 8p(8p – 1)(8p + 1) là tích của 3 số tự nhiên liên tiếp.
Suy ra 8p(8p – 1)(8p + 1) chia hết cho 3.
Lại có 8p – 1 > 3 (p ∈ ℕ).
Suy ra 8p – 1 không chia hết cho 3.
Do đó 8p + 1 chia hết cho 3.
Mà 8p + 1 > 3, p ∈ ℕ.
Suy ra 8p + 1 là hợp số.
Vậy 8p + 1 là hợp số; 8p – 1 là số nguyên tố.
Đề bài. Cho hai tập hợp A={1;2;3} và B ={1;2;3;4;5}. Có tất cả bao nhiêu tập X thỏa mãn A ⊂ X ⊂ B?
Lời giải:
Ta có: A ⊂ X nên X có ít nhất 3 phần tử {1; 2; 3}.
Ta có: X ⊂ B nên X phải có nhiều nhất 5 phần tử và các phần tử X cũng thuộc B
Do đó các tập X thỏa mãn là {1; 2; 3}, {1; 2; 3; 4}, {1; 2; 3; 5}, {1; 2; 3; 4; 5}.
Lời giải:
Chọn B
Điểm cuối của α thuộc góc phần tư thứ hai nên .
Lời giải:
+ Goi v13 là vận tốc của xuồng đối với bờ
v23 là vận tốc của dòng nước đối với bờ sông.
v12 là vận tốc của xuồng đối với nước: v12 = 36km/h
+ Khi xuôi dòng:
v13 = v12+v23 = 36 + v23
+ Khi ngược dòng:
v'13 = v12−v23 = 36 – v23
v13 + v'13 =
Vậy S = 86,4km.
Đề bài. Cho tia Ox, vẽ hai tia Oy và Ot nằm cùng phía với đường thẳng chứa tia Ox sao cho: .
a) Tính ? Tia Oy có là tia phân giác của không? Vì sao?
b) Gọi tia Om là tia đối của tia Ox. Tính số đo của ?
c) Gọi Oz là tia phân giác của . Hỏi tia Oz có vuông góc với tia Oy không?
Lời giải:
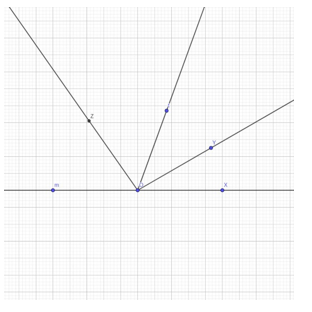 a) Ta có:
a) Ta có:
Oy, Ot ∈ nửa mặt phẳng có bờ là đường thẳng Ox
Nên Oy nằm giữa Ox, Ot
Suy ra:
Suy ra: nên Oy không phải là phân giác
b) Ta có:
c) Ta có: Oz là tia phân giác nên:
Suy ra:
Nên: Oz và Oy không vuông góc.
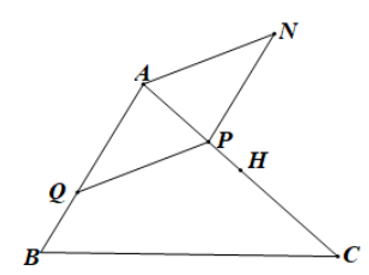
a) Tìm giao tuyến của (OMN) và (BCD).
b) Tìm giao điểm của BC với (OMN).
c) Tìm giao điểm của BD với (OMN).
Lời giải:
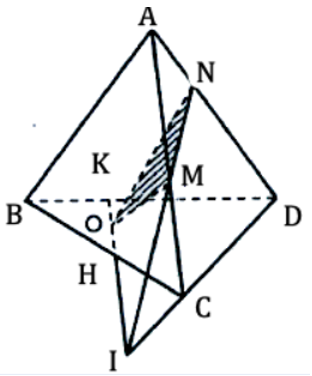 a) Trong mp(ACD) gọi I là giao điểm của NM và CD.
a) Trong mp(ACD) gọi I là giao điểm của NM và CD.
Khi đó OI = (OMN) ∩ (BCD)
b) Trong mp(BCD) gọi H, K là giao điểm OI với BC và BD
K, H ∈ OI nên K, H ∈ (OMN)
Vậy H = BC ∩ (OMN)
c) K, H ∈ OI nên K, H ∈ (OMN)
Nên K = BD ∩ (OMN).
Lời giải:
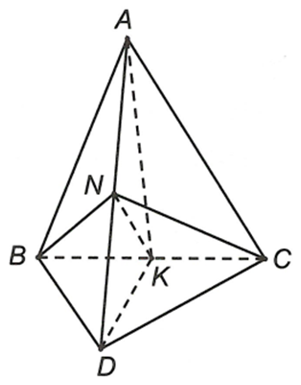 Ta có điểm M, N là hai điểm chung của hai mặt phẳng (BCM) và (AND) nên MN = (BCM) ∩ (AND).
Ta có điểm M, N là hai điểm chung của hai mặt phẳng (BCM) và (AND) nên MN = (BCM) ∩ (AND).
Lời giải:
NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2): (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
⇒ Q = AC ∩ (MNP). Có:
⇒MQ // NP // AB
Theo định lý Ta-lét ta có: .
Lời giải:
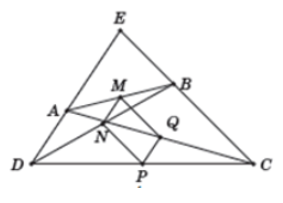 Giả sử AD cắt BC tại E
Giả sử AD cắt BC tại E
Khi đó từ giả thiết: ta có:
Ta lần lượt có: MN // AD // PQ; MQ // BC // PN
Do đó dựa trên tính chất của góc có cạnh tương ứng song song ta được:
Do đó bốn điểm M, N, P, Q cùng nằm trên một đường tròn đường kính NQ.
Đề bài. Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Lời giải:
a) Nửa chu vi của tam giác ABC là:
p = (15 + 18 + 27) : 2 = 30
Áp dụng công thức Heron ta tính được diện tích tam giác ABC là:
S =
Mặt khác S = pr (r là bán kính đường tròn nội tiếp tam giác ABC)
Suy ra
Vậy diện tích tam giác ABC là (đơn vị diện tích) ; bán kính đường tròn nội tiếp tam giác ABC là (đơn vị dộ dài).
b) Do G là trọng tâm tam giác ABC nên G chia tam giác ABC thành ba tam giác GAB, GAC, GBC có diện tích bằng nhau.
Suy ra
Vậy diện tích của tam giác GBC là : (đơn vị diện tích).
Đề bài. Cho tứ giác ABCD có . Tính .
Lời giải:
Ta có: (tổng các góc của tứ giác)
.
Lời giải:
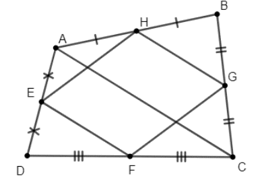 • EF là đường trung bình của tam giác ABC, nên ta suy ra được EF // AC (1)
• EF là đường trung bình của tam giác ABC, nên ta suy ra được EF // AC (1)
• HG là đường trung bình của tam giác ADC, nên ta suy ra được HG // AC (2)
Từ (1) và (2) suy ra EF // HC
Tương tự ta có:
• FG là đường trung bình của tam giác BDC, nên FG // BD (3)
• EH là đường trung bình của tam giác BDA, nên EH // BD (4)
Từ (3) và (4) ta có FG // EH
Xét tứ giác EFGH ta có: EF // HG và FG // EH.
Do đó suy ra tứ giác EFGH là hình bình hành.
Lời giải:
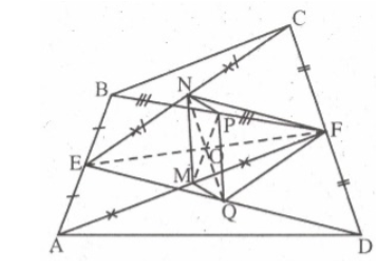 Xét tam giác ABF có: E là trung điểm AB, P là trung điểm BF nên EP là đường trung bình của tam giác ABF
Xét tam giác ABF có: E là trung điểm AB, P là trung điểm BF nên EP là đường trung bình của tam giác ABF
Suy ra: EP // AF và
M là trung điểm AF nên:
Xét tứ giác EPFM có: EP // MF và EP = MF nên EPFM là hình bình hành
Suy ra: EF và PQ cắt nhau tại trung điểm O mỗi đường
Chứng minh tương tự: EMFP là hình bình hàng nên EF và MP cắt nhau tại trung điểm mỗi đường.
Suy ra: MP và NQ cắt nhau tại trung điểm O mỗi đường.
Vậy MNPQ là hình bình hành.
Lời giải:
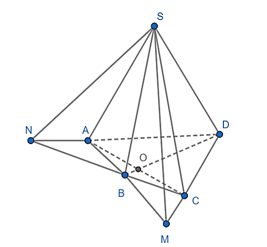 Kéo dài AB và CD cắt nhau tại M, kéo dài AD và BC cắt nhau tại N
Kéo dài AB và CD cắt nhau tại M, kéo dài AD và BC cắt nhau tại N
Gọi O là giao điểm của AC và BD
(SAB) ∩ (SCD) = SM vì S ∈ (SAB) và (SCD)
M ∈ AB ⊂ (SAB); N ∈ CD ⊂ (SCD) nên M = (SAB) ∩ (SCD)
Làm tương tự: (SAD) ∩ (SBC) = SN
(SAC) ∩ (SBD) = SO.
Đề bài. Cho tứ giác ABCD, tìm điểm M thỏa mãn
Lời giải:
Ta có:
⇔
⇔
⇔
⇔
Vậy M đối xứng với B qua C hay C là trung điểm của BM.
Đề bài. Tìm x, y, z là các số dương biết (x2 + 1)(y2 + 4)(z2 + 9) = 48xyz.
Lời giải:
Áp dụng bất đẳng thức AM-GM ta có:
x2 + 1 ≥
y2 + 4 ≥
z2 + 9 ≥
Suy ra: (x2 + 1)(y2 + 4)(z2 + 9) ≥ 2x.4y.6z = 48xyz
Mà theo giả thiết (x2 + 1)(y2 + 4)(z2 + 9) = 48xyz
Nên dấu “=” xảy ra khi: (vì x, y, z > 0).
Đề bài. Cho x – y = 1. Tính giá trị của biểu thức x3 − y3 − 3xy.
Lời giải:
x3 − y3 − 3xy
= (x – y)3 + 3xy(x – y)
= 1 + 3xy – 3xy
= 1.