Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 107)

Minh Nguyệt Ngày: 06-12-2024 Tổng hợp kiến thức

201

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 107)

Câu 1: Phân tích đa thức thành nhân tử: 9(x+5)² - (x-7)²

Phương pháp giải:

Nhóm đa thức theo hiệu hai bình phương

Áp dụng công thức hiệu hai bình phương

$a^2 - b^2 = (a - b)(a + b)$

Rút gọn biểu thức bên trong

Nhân thêm hằng số chung nếu cần thiết

Lời giải:

= [3(x + 5)]²- (x - 7)²

= (3x + 15 + x - 7)(3x + 15 - x + 7)

= (4x + 8)(2x + 22)

= 8(x + 2)(x + 11)

Một số phương pháp phân tích đa thức thành nhân tử:

Phương pháp đặt nhân tử chung

+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.

Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.

( lưu ý tính chất: A = -(-A)).

Phương pháp dùng hằng đẳng thức

+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.

+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.

Phương pháp nhóm hạng tử

+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.

+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thế phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.

+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.

Chú ý

+ Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.

+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).

+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.

+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.

Phối hợp nhiều phương pháp

Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:

+ Đặt nhân tử chung

+ Dùng hằng đẳng thức

+ Nhóm nhiều hạng tử và phối hợp chúng

⇒ Để phân tích đa thức thành nhân tử.

Chú ý

Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.

Câu 2: Cho (P): y = ax². Tìm a để (P) đi qua M(1, 2). Với a tìm được, tìm tọa độ giao điểm của (P) và (d): y = 3x - 1

Phương pháp giải:

Xác định hệ số $a$ .

Tìm tọa độ giao điểm của $(P)$ và $(d): y = 3x - 1$

Giải phương trình bậc 2

Dùng công thức nghiệm: $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Với $a = 2, b = -3, c = 1$ , ta tìm được nghiệm $x_1$ và $x_2$ .

Thay $x_1, x_2$ vào $y = 3x - 1$ để tìm tọa độ giao điểm.

Lời giải:

(P) đi qua điểm $M (1; 2)$ ta thay ${\begin{array}{c} x = 1 \\ y = 2 \end{array}$ vào (P) ta có:
$2 = a \cdot 1^{2}$

$\Leftrightarrow a = 2$

$\Rightarrow (P) : y = 2 x^{2}$

Ta có phương trình hoành độ giao điểm của (P) và (d) là: $2 x^{2} = 3 x - 1$

$\Leftrightarrow 2 x^{2} - 3 x + 1 = 0$

$Δ = {(- 3)}^{2} - 4 \cdot 2 \cdot 1 = 1 > 0$

Có 2 nghiệm phân biệt

Tọa độ giao điểm (1) là:

$x_{1} = \frac{3 + \sqrt{1}}{2 \cdot 2} = 1 \Rightarrow y_{1} = 2 \cdot 1^{2} = 2$

Tọa độ giao điểm (2) là:

$x_{2} = \frac{3 - \sqrt{1}}{2 \cdot 2} = \frac{1}{2} \Rightarrow y_{2} = 2 \cdot {(\frac{1}{2})}^{2} = \frac{1}{2}$

Câu 3: Cho x, y là 2 số thực thỏa mãn $x y \geq 1$ . CMR $\frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}} \geq \frac{2}{1 + x y}$

Phương pháp giải:

Xử lý biểu thức vế trái.

Áp dụng bất đẳng thức và xét điều kiện $x y \geq 1$ .

Đánh giá vế trái và kết luận.

Lời giải:

$V T = \frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}} = \frac{2 + x^{2} + y^{2}}{1 + y^{2} + x^{2} + x^{2} y^{2}}$

Ta luôn có: ${(a - b)}^{2} \geq 0$ $\Leftrightarrow$ $a^{2} - 2 a b + b^{2} \geq 0$ $\Leftrightarrow$ $a^{2} + b^{2} \geq 2 a b$

Dấu "=" xảy ra $\Leftrightarrow$ $a = b$

Áp dụng BĐT trên ta có: $x^{2} + y^{2} \geq 2 x y$ mà $x y \geq 1$ nên $x^{2} + y^{2} \geq 2$

$x y \geq 1$ $\Rightarrow$ ${(x y)}^{2} = x^{2} y^{2} \geq 1$

Khi đó: $V T = \frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}} = \frac{1 + x^{2} + y^{2}}{1 + x^{2} + y^{2} + x^{2} y^{2}} \geq \frac{2 x y + 1}{2 x y + 1 + 1} \geq \frac{2 + 2}{2 x y + 2} = \frac{4}{2 (x y + 1)} = \frac{2}{1 + x y}$

$\Rightarrow$ $V T \geq \frac{2}{1 + x y}$ hay $\frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}} \geq \frac{2}{1 + x y}$ (đpcm)

Câu 4: Tính nhanh (372 - 19 x 4) + (981:9 - 13)

Phương pháp giải:

Thực hiện các phép tính trong ngoặc trước

Cộng các kết quả vừa tính

Lời giải:

(372 - 19 x 4) + (981:9 - 13)

= (372 - 76) + (109 - 13)

= 296 + 96

= 392

Phương pháp chung

* Các tính chất của phép cộng như sau:

+ Tính giao hoán: a + b = b + a.

+ Tính kết hợp: (a + b) + c = a + (b + c).

+ Cộng với số 0: a + 0 = 0 + a = a

+ Cộng với số đối: a + (-a) = 0

* Để tính nhanh, tính hợp lí giá trị một biểu thức ta có thể làm theo các cách sau:

- Áp dụng các tính chất của phép cộng để nhóm các số lại với nhau sao cho tổng của mỗi nhóm là một số tròn trục, tròn trăm…

- Nhóm các số lại với nhau sao cho mỗi nhóm có cùng kết quả, sau đóthực hiện cộng các số đã nhóm.

Câu 5: Tìm các số tự nhiên x, y sao cho $\frac{x}{9} - \frac{3}{y} = \frac{1}{18}$

Phương pháp giải:

Đưa phương trình ban đầu về dạng không còn mẫu số.

Giải phương trình và tìm x.

Kiểm tra lại x với điều kiện và kết luận.

Lời giải:

Ta có: $\frac{x y - 27}{9 y} = \frac{1}{18}$

=> 18(xy - 27) = 9y <=> 18xy - 486 = 9y

<=> 2xy - 54 = y

<=> 2xy - y = 54

<=> y(2x - 1) = 54

=> y = $\frac{54}{2 x - 1}$

=> 2x - 1 thuộc Ư(54) = {1; 2; 3; 6; 9; 18; 27; 54}

Vì 2x - 1 là lẻ => Ta loại bỏ được: {2; 6; 18; 54}

Thay: 2x - 1 = 1 => x = 1; y = 54 (TM)

2x - 1 = 3 => x = 2; y = 18 (TM)

2x - 1 = 9 => x = 5; y = 6 (TM)

2x - 1 = 27 => x = 14; y = 2 (TM)

Vậy: x = 1; y = 54

x = 2; y = 18

x = 5; y = 6

x = 14; y = 2

=> Thỏa mãn yêu cầu đề bài

Câu 6: Cho x + y + z = 0. Chứng minh $2 (x^{4} + y^{4} + z^{4}) = {(x^{2} + y^{2} + z^{2})}^{2}$

Phương pháp giải:

Sử dụng điều kiện $x + y + z = 0$ và các khai triển để chứng minh hai vế của phương trình.

Lời giải:

${(x + y + z)}^{2} = x^{2} + y^{2} + z^{2} + 2 x y + 2 y z + 2 x z$

Thay x + y + z = 0 vào

$\Rightarrow 0 = x^{2} + y^{2} + z^{2} + 2 (x y + y z + x z)$

$\Leftrightarrow x^{2} + y^{2} + z^{2} = - 2 (x y + y z + x z)$ (1)

Ta có

${(x^{2} + y^{2} + z^{2})}^{2} = x^{4} + y^{4} + z^{4} + 2 x^{2} y^{2} + 2 y^{2} z^{2} + 2 x^{2} z^{2}$ (2)

Bình phương 2 vế của (1)

${(x^{2} + y^{2} + z^{2})}^{2} = 4 {(x y + y z + x z)}^{2}$

$\Leftrightarrow {(x^{2} + y^{2} + z^{2})}^{2} = 4 (x^{2} y^{2} + y^{2} z^{2} + x^{2} z^{2} + 2 x y^{2} z + 2 x y z^{2} + 2 x^{2} y z)$

$\Leftrightarrow {(x^{2} + y^{2} + z^{2})}^{2} = 4 [x^{2} y^{2} + y^{2} z^{2} + x^{2} z^{2} + 2 x y z (x + y + z)]$

Do x + y + z = 0 nên

${(x^{2} + y^{2} + z^{2})}^{2} = 4 (x^{2} y^{2} + y^{2} z^{2} + x^{2} z^{2})$

$\Rightarrow \frac{{(x^{2} + y^{2} + z^{2})}^{2}}{2} = 2 x^{2} y^{2} + 2 y^{2} z^{2} + 2 x^{2} z^{2}$ (3)

Thay (3) vào (2)

${(x^{2} + y^{2} + z^{2})}^{2} = x^{4} + y^{4} + z^{4} + \frac{{(x^{2} + y^{2} + z^{2})}^{2}}{2}$

$\Rightarrow 2 (x^{4} + y^{4} + z^{4}) = {(x^{2} + y^{2} + z^{2})}^{2}$ (đpcm)

Câu 7: Tính

a) $\frac{2}{3} + \frac{3}{4} + \frac{5}{6} =$

b) $\frac{1}{2} + \frac{4}{5} + \frac{12}{25} =$

c) $\frac{5}{6} . (\frac{4}{15} + \frac{2}{3}) =$

d) $\frac{13}{9} : \frac{5}{6} : \frac{7}{15} =$

Phương pháp giải:

Quy đồng biểu thức trên, đưa về cùng mẫu số.

Kết luận và rút gọn (nếu có).

Lời giải:

a) $\frac{2}{3} + \frac{3}{4} + \frac{5}{6}$

$=$ $\frac{8}{12} + \frac{9}{12} + \frac{10}{12}$

$=$ $\frac{27}{12}$

b) $\frac{1}{2} + \frac{4}{5} + \frac{12}{25}$

$=$ $\frac{25}{50} + \frac{40}{50} + \frac{24}{50}$

$= \frac{89}{50}$

c) $\frac{5}{6} . (\frac{4}{15} + \frac{2}{3})$

$= \frac{5}{6} . (\frac{4}{15} + \frac{6}{15})$

$= \frac{5}{6} . \frac{2}{5}$

$= \frac{10}{30}$

$=$ $\frac{1}{3}$

d) $\frac{13}{9} : \frac{5}{6} : \frac{7}{15}$

$= \frac{13}{9} . \frac{6}{5} . \frac{15}{7}$

$= \frac{13.6.15}{9.5.7}$

$= \frac{13.2}{7}$

$= \frac{26}{7}$

Công thức

a) Phép cộng hai phân số:

⦁ Cộng hai phân số cùng mẫu: $\frac{a}{m} + \frac{b}{m} = \frac{a + b}{m}$ (với a, b, m ∈ ℤ và m ≠ 0).

⦁ Cộng hai phân số khác mẫu: Quy đồng mẫu số của phân số để đưa về phép cộng hai phân số cùng mẫu.

b) Phép trừ hai phân số:

⦁ Số đối: $\frac{a}{b} + (- \frac{a}{b}) = 0$ (với a, b ∈ ℤ và b ≠ 0).

⦁ Trừ hai phân số cùng mẫu: $\frac{a}{m} - \frac{b}{m} = \frac{a - b}{m}$ (với a, b, m ∈ ℤ và m ≠ 0).

⦁ Trừ hai phân số khác mẫu: Quy đồng mẫu số của phân số để đưa về phép trừ hai phân số cùng mẫu.

Chú ý:

– Muốn trừ hai phân số ta có thể cộng số bị trừ với số đối của số trừ.

$\frac{a}{b} - \frac{c}{d} = \frac{a}{b} + - (\frac{c}{d})$ (với a, b, c, d ∈ ℤ và b, d ≠ 0).

– Sau khi thực hiện phép cộng và phép trừ phân số, ta rút gọn kết quả (nếu có).

Câu 8: Không cần tính hãy cho biết tổng và hiệu có chia hết cho 3 không?

a. 240 + 123

b. 240 - 123

Phương pháp giải:

Để kiểm tra xem tổng và hiệu có chia hết cho 3 hay không, chúng ta có thể áp dụng quy tắc chia hết cho 3: Một số chia hết cho 3 nếu tổng các chữ số của nó chia hết cho 3.

Lời giải:

a) 240 có tổng các chữ số là 6

=> chia hết cho 3

124 tổng các chữ số là 6

=> chia hết cho 3

=> 240 + 123 chia hết cho 3

b) Vì 240 chia hết cho 3 và 123 chia hết cho 3

=> 240 - 123 chia hết cho 3

Tính chất chia hết

Tính chất 1

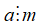
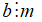
Nếu Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án và thì

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.

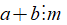
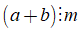
+ Ta có thể viết Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án hoặc đều được.

Chú ý:

• Tính chất 1 cũng đúng đối với một hiệu

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

• Tính chất 1 cũng đúng với một tổng nhiều số hạng

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

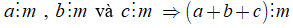
Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án Tính chất 2

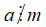
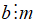
Nếu Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án và thì

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

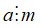
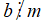
Nếu Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án và thì

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.

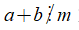
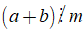
+ Ta có thể viết Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án hoặc đều được.

Chú ý:

• Tính chất 2 cũng đúng đối với một hiệu

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

• Tính chất 2 cũng đúng với một tổng nhiều số hạng, trong đó chỉ có một số hạng không chia hết cho m, các số hạng còn lại đều chia hết cho m:

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số , còn các số hạng còn lại đều chia hết cho số đó thì tổng đó không chia hết cho số đó.

Toán lớp 6 | Lý thuyết - Bài tập Toán 6 có đáp án

Câu 9: Một hội trường có 32 chỗ ngồi cho 1 hàng ghế. Nếu có 890 đại biểu tham dự họp thì phải dùng ít nhất bao nhiêu hàng ghế

Phương pháp giải:

Để tìm số hàng ghế cần dùng, ta chia tổng số đại biểu cho số chỗ ngồi của mỗi hàng ghế. Sau đó, nếu có phần dư, ta sẽ làm tròn lên một hàng ghế nữa.

Lời giải:

Phải dùng số hàng ghế là :

890 : 32 = 27 (dư 26)

Có 890 đại biểu thì có 27 hàng ghế 32 chỗ, còn dư 26 đại biểu

Vậy phải dùng ít nhất 28 hàng ghế.

Câu 10: Thế nào là 2 góc tương ứng?

Thế nào là 2 cạnh tương ứng?

Phương pháp giải:

2 góc tương ứng:
Khi hai đường thẳng song song bị cắt bởi một đường chéo (hay đường thẳng cắt), các góc được tạo ra ở các vị trí đối xứng nhau và nằm ở cùng một phía của đường thẳng cắt, được gọi là góc tương ứng. Hai góc này có giá trị bằng nhau nếu hai đường thẳng song song.

2 cạnh tương ứng:
Khi hai tam giác có các góc tương ứng bằng nhau (tam giác đồng dạng), các cạnh tương ứng trong hai tam giác đó có tỉ lệ bằng nhau. Cạnh tương ứng là những cạnh nằm đối diện với các góc tương ứng trong tam giác.

Lời giải:

Hai góc tương ứng: Là hai góc được hình thành khi một đường thẳng cắt hai đường thẳng song song, có vị trí đối xứng và nằm cùng một phía của đường thẳng cắt.

Hai cạnh tương ứng: Là hai cạnh trong các tam giác đồng dạng, tương ứng với các góc tương ứng, có tỉ lệ với nhau.

Câu 11: Một học sinh đi từ nhà tới trường, sau khi đi được $\frac{1}{4}$ quãng đường thì chợt nhớ mình quên mất một cuốn sách nên vội trở về nhà rồi đi ngay đến trường và muộn 15 phút

a. Tính vận tốc của học sinh biết quãng đường S từ nhà tới trường là 6km ?

b. Để đến trường đúng thời gian dự định thì khi quay về nhà và đi lần 2 em phải đi với vận tốc là bao nhiêu ?

Phương pháp giải:

Tính quãng đường đã đi:

Quãng đường đi 1/4 + quay lại = $2 \times \frac{1}{4}S$ .

Tổng quãng đường = $S + 2 \times \frac{1}{4}S$ .

Tính vận tốc hiện tại:

Vận tốc $v = \frac{\text{quãng đường đi thực tế}}{\text{thời gian đã đi}}$ .

Tính vận tốc cần thiết:

Vận tốc để đúng giờ: $v = \frac{\text{tổng quãng đường thực đi}}{\text{thời gian dự kiến}}$ .

Lời giải:

$\frac{1}{4}$ quãng đường từ nhà đến trường : $\frac{1}{4}$ x 6 = 1,5 km

15 phút = $\frac{1}{4}$ giờ

Vận tốc của hs đó : (1,5 x 2) : $\frac{1}{4}$ = 12 km/giờ

Quãng đường thực đi của HS đó : 6 + (1,5 x 2) = 9 km

Để không muộn 15 phút thì hs đó phải đi với vận tốc : $\frac{9}{6}$ x 12 = 18 km/giờ

Câu 12: Khai triển hằng đẳng thức $a^{4} + b^{4}$

Phương pháp giải:

Áp dụng hằng đẳng thức hiệu hai bình phương:

${(a^{2} + b^{2})}^{2} - {(\sqrt{2} \cdot a \cdot b)}^{2} = (a^{2} + b^{2} + \sqrt{2} \cdot a \cdot b) \cdot (a^{2} + b^{2} - \sqrt{2} \cdot a \cdot b)$

Lời giải:

$a^{4} + b^{4} = (a^{4} + 2 a^{2} b + b^{4}) - 2 a^{2} b^{2}$

$= {(a^{2} + b^{2})}^{2} - {(\sqrt{2} . a . b)}^{2} = (a^{2} + b^{2} + \sqrt{2} . a . b) (a^{2} + b^{2} + \sqrt{2} . a . b)$

Câu 13: Tìm x biết: $(\frac{6}{7} - \frac{3}{5}) : \frac{2 x}{3} = \frac{- 11}{8}$

Phương pháp giải:

Tiến hành phép tính trong dấu ngoặc và đơn giản hóa.

Thay vào biểu thức và giải phương trình.

Lời giải:

$(\frac{6}{7} - \frac{3}{5}) : \frac{2 x}{3} = \frac{- 11}{8}$

$\Leftrightarrow \frac{9}{35} : \frac{2 x}{3} = \frac{- 11}{8}$

$\Leftrightarrow \frac{9}{35} . \frac{3}{2 x} = \frac{- 11}{8}$

$\Leftrightarrow \frac{27}{70 x} = \frac{- 11}{8}$

$\Leftrightarrow - 770 x = 216$

$\Leftrightarrow x = \frac{- 108}{385}$

Phương pháp chung

Để tìm số hữu tỉ x, ta có thể thực hiện như sau:

− Sử dụng tính chất của các phép toán.

− Sử dụng quan hệ giữa các số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương trong một phép chia.

− Sử dụng quy tắc dấu ngoặc, chuyển vế.

Với a, b, c là các số hữu tỉ:

+ Quy tắc dấu ngoặc:

a + (b – c) = a + b – c;

a – (b – c + d) = a – b + c – d.

+ Quy tắc chuyển vế:

a + b = c thì a = c – b;

a – b = c thì a = c + b.

Chú ý: Ta có thể sử dụng tính chất tích hai số bằng 0 thì một trong hai số đó bằng 0 để tìm số hữu tỉ x.

Câu 14: Quãng đường AB dài 123 km. Cùng một lúc một ô tô đi từ A về B và một xe máy đi từ B về A. Sau 1 giờ 30 phút thì hai xe gặp nhau. Tính vận tốc của mỗi xe, biết rằng vận tốc của ô tô hơn vận tốc của xe máy là 8 km/giờ.

Phương pháp giải:

Tính tổng vận tốc: dựa vào tổng quãng đường và thời gian gặp nhau.

Tính vận tốc của ô tô và xe máy.

Lời giải:

1 giờ 30 phút = 1,5 giờ

Tổng vận tốc của cả ô tô và xe máy là :

123 : 1,5 = 82 ( km/giờ )

Vận tốc của ô tô là :

( 82 + 8 ) : 2 = 45 ( km/giờ )

Vận tốc của xe máy là :

45 - 8 = 37 (km/giờ)

Đ/s : ô tô : 45 km/giờ

xe máy : 37 km/giờ

Câu 15: Cho hệ phương trình: ${\begin{array}{c} x + 2 y = 2 \\ m x - y = m \end{array}$ (m là tham số)

a) Giải là biện luận hệ phương trình đã cho theo m.

b) Trong trường hợp hệ phương trình có 1 nghiệm duy nhất (x,y). Tìm hệ thức liên hệ giữa x và y ko phụ thuộc vào m

Phương pháp giải:

Sử dụng lý thuyết biện luận hệ phương trình bậc nhất hai ẩn.

Phương pháp thế: Ta thay giá trị $x$ từ phương trình đầu tiên vào phương trình thứ hai để giảm bài toán về một phương trình với một ẩn.

Biện luận các trường hợp: Dựa vào điều kiện có nghiệm duy nhất, vô số nghiệm hoặc vô nghiệm của hệ, ta xét ba trường hợp:

Nghiệm duy nhất khi hệ phương trình có một nghiệm xác định.

Vô số nghiệm khi hệ phương trình có vô số nghiệm (tương đương với phương trình trở thành phương trình xác định với một ẩn).

Vô nghiệm khi phương trình không thể thỏa mãn bất kỳ giá trị nào của các ẩn.

Xử lý điều kiện tham số: Cụ thể, ta tìm các giá trị của tham số $m$ mà tại đó hệ phương trình có nghiệm duy nhất, vô số nghiệm hoặc vô nghiệm.

Giải phương trình: Sau khi biện luận, ta tiếp tục giải phương trình để tìm mối quan hệ giữa $x$ và $y$ , từ đó rút ra kết luận về nghiệm của hệ phương trình.

Lời giải:

${\begin{array}{c} x + 2 y = 2 \\ m x - y = m \end{array} \Leftrightarrow {\begin{array}{c} x = 2 - 2 y \\ m (2 - 2 y) - y - m = 0 \end{array}$

$\Leftrightarrow {\begin{array}{c} x = 2 - 2 y \\ 2 m - 2 m y - y - m = 0 \end{array} \Leftrightarrow {\begin{array}{c} x = 2 - 2 y \\ (- 2 m - 1) y + m = 0 (.) \end{array}$

a, Hệ pt có 1 nghiệm duy nhất khi pt (.) có nghiệm duy nhất

$\Rightarrow - 2 m - 1 \neq 0 \Leftrightarrow - 2 m \neq 1 \Leftrightarrow m \neq \frac{- 1}{2}$

Hệ pt có vô số nghiệm khi pt (.) có vô số nghiệm

$\Rightarrow {\begin{array}{c} - 2 m - 1 = 0 \\ m = 0 \end{array} \Leftrightarrow {\begin{array}{c} m = \frac{- 1}{2} \\ m = 0 \end{array}$ (vô lí)

Hệ pt vô nghiệm khi pt (.) vô nghiệm

$\Rightarrow {\begin{array}{c} - 2 m - 1 = 0 \\ m \neq 0 \end{array} \Leftrightarrow {\begin{array}{c} m = \frac{- 1}{2} (t h o ả m a n) \\ m \neq 0 \end{array}$

$\Rightarrow m = \frac{- 1}{2}$

b, Với m $\neq \frac{- 1}{2}$ , ta có:

${\begin{array}{c} x = 2 - 2 y \\ y = \frac{- m}{- 2 m - 1} = \frac{2}{2 m + 1} \end{array}$

Câu 16: Tính giá trị biểu thức sau: 5 000 000 : 5000000 + 100000 : 2

Phương pháp giải:

Thực hiện chia từng số trong biểu thức.

Cộng các kết quả đã tìm được và kết luận.

Lời giải:

5 000 000 : 5 000 000 + 100000 : 2

= 1 + 50000

= 50001

Câu 17: Để ép được 5l nước dứa người ta cần 15 kg dứa quả. 7350 kg dứa quả thì ép được bao nhiêu lít nước dứa?

Phương pháp giải:

Tìm khối lượng dứa cần để ép 1 lít nước dứa.

Tính số lít nước ép được từ 7350 kg dứa.

Lời giải:

1l nước dứa cần số ki lô gam dứa là :

15 : 5 = 3 (kg)

7350 ki lô gam dứa ép được số lít nước dứa là :

7350 : 3 = 2450 ( lít )

Đáp số : 2450 lít nước dừa

Phương pháp chung để giải các bài toán:

* Bước 1: Đọc kĩ đề toán: Cần nắm được ba yếu tố cơ bản. Những “dữ kiện” là những cái đã cho, đã biết trong đầu bài, “những ẩn số” là những cái chưa biết và cần tìm và những “điều kiện” là quan hệ giữa các dữ kiện với ẩn số.

* Bước 2: Phân tích bài toán.

- Bài toán cho biết gì?

- Bài toán hỏi gì?

- Muốn tìm cái đó ta cần biết gì?

- Cái này biết chưa?

- Còn cái này thì sao?

- Muốn tìm cái chưa biết ta cần dựa vào đâu? Làm như thế nào?

* Bước 3: Tóm tắt đề toán.

* Cách 1: Tóm tắt bằng chữ.

* Cách 2: Tóm tắt bằng chữ và dấu.

* Cách 3: Tóm tắt bằng sơ đồ đoạn thẳng.

* Cách 4: Tóm tắt bằng hình tượng trưng.

* Cách 5: Tóm tắt bằng lưu đồ.

* Cách 6: Tóm tắt bằng sơ đồ Ven

* Cách 7: Tóm tắt băng kẻ ô.

* Bước 4: Viết bài giải.

* Bước 5: Kiểm tra lời giải và đánh giá cách giải.

- Đọc lại lời giải.

- Kiểm tra các bước giải xem đã hợp lí yêu cầu của bải chưa, các câu văn diễn đạt trong lời giải đúng chưa.

- Thử lại các kết quả vừa tính từ bước đầu tiên.

- Thử lại kết quả đáp số xem đã phù hợp với yêu cầu của đề bài chưa.

Câu 18: Tìm x : ${11.6}^{x - 1} + {2.6}^{x + 1} = {11.6}^{11} + {2.6}^{13}$

Phương pháp giải:

Biến đổi các mũ theo cùng cơ số:

Đưa $6^{x+1}$ và $6^{x-1}$ về dạng $6^x$ .

Nhóm và đặt ẩn chung:

Đặt $6^{x-1}$ làm nhân tử chung.

So sánh các hệ số tương ứng:

Đưa về phương trình đơn giản và giải $x$ .

Lời giải:

${11.6}^{x - 1} + {2.6}^{x + 1} = {11.6}^{11} + {2.6}^{13}$

=> $11. 6^{x - 1} + 2. 6^{x - 1 + 2} = 11. 6^{11} + 2. 6^{11 + 2}$

=> $11. 6^{x - 1} + 2. 6^{x - 1} . 6^{2} = 11. 6^{11} + 2. 6^{11} . 6^{2}$

=> $6^{x - 1} (11 + 2. 6^{2}) = 6^{11} (11 + 2. 6^{2})$

=> $6^{x - 1} = 6^{11}$

=> x - 1 = 11

=> $x = 12$

Câu 19: Tại sao số 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương?

Phương pháp giải:

Xác định định nghĩa về số hữu tỉ dương và số hữu tỉ âm.

Xét vị trí của số 0 trong trục số để kết luận.

Lời giải:

Vì: Trong số hữu tỷ chia ra ba loại:

Số hữu tỷ dương là những số lớn hơn 0

Sô hữu tỷ âm là những số nhỏ hơn 0

=> Số 0 ko là số hữu tỉ dương cũng không là số hữu tỉ âm !

Câu 20: Có tất cả bao nhiêu số tự nhiên có 4 chữ số mà chúng đều nhỏ hơn 2011?

Phương pháp giải:

Xác định số tự nhiên 4 chữ số nhỏ nhất và lớn nhất thỏa mãn điều kiện.

Tính số lượng các số bằng công thức: $(\text{số cuối} - \text{số đầu}) : 1 + 1$ .

Lời giải:

Số đầu : 1000

Số cuối : 2010

Có tất cả là :

(2010 - 1000 ) : 1 + 1 = 1011

Đáp số : 1011

Câu 21: Cho tam giác ABC nhọn. CMR: $\sin^{2} A + \sin^{2} B + \sin^{2} C \leq \frac{9}{4}$

Phương pháp giải:

Biểu diễn tổng $\sin^2 A + \sin^2 B + \sin^2 C$ : Sử dụng công thức $\sin^2 x = \frac{1 - \cos 2x}{2}$ để chuyển sang dạng có liên quan đến hàm cos.

Tính chất góc trong tam giác: Sử dụng tính chất $A + B + C = 180^\circ$ , từ đó suy ra mối liên hệ giữa $\cos(A + B)$ và $\cos C$ .

Áp dụng bất đẳng thức:

Với tam giác nhọn: $\cos C > 0$ và $0 < \cos(A - B) \leq 1$ .

Suy ra $\cos C \cdot \cos(A - B) \leq \cos C$ .

Đánh giá giá trị lớn nhất: Biến đổi để đưa về dạng $\frac{9}{4} - (\cos C - \frac{1}{2})^2 \leq \frac{9}{4}$ , đạt dấu "=" khi tam giác đều ( $A = B = C = 60^\circ$ ).

Kết luận: Bất đẳng thức đúng và dấu "=" xảy ra khi tam giác đều.

Lời giải:

$V T = s i n^{2} A + s i n^{2} B + s i n^{2} C = \frac{1 - c o s 2 A}{2} + \frac{1 - c o s 2 B}{2} + 1 - c o s^{2} C$

$= 2 - (c o s 2 A + c o s 2 B) - c o s^{2} C = 2 - c o s (A + B) c o s (A - B) - c o s^{2} C$

$= 2 + c o s C . c o s (A - B) - c o s^{2} C$

Mà ABC là tam giác nhọn $\Rightarrow {\begin{array}{c} c o s C > 0 \\ 0 < c o s (A - B) \leq 1 \end{array}$

$\Rightarrow c o s C . c o s (A - B) \leq c o s C$

$\Rightarrow V T \leq 2 + c o s C - c o s^{2} C = \frac{9}{4} - {(c o s C - \frac{1}{2})}^{2} \leq \frac{9}{4}$

Dấu "=" xảy ra khi ABC là tam giác đều

Câu 22: Tính giá trị của biểu thức:

a, $12 \frac{1}{3} - (3 \frac{3}{4} + 4 \frac{3}{4})$

b, $3 \frac{5}{6} + 2 \frac{1}{6} . 6$

c, $3 \frac{1}{2} + 4 \frac{5}{7} - 5 \frac{5}{14}$

d, $4 \frac{1}{2} + \frac{1}{2} : 5 \frac{1}{2}$

Phương pháp giải:

Chuyển hỗn số sang phân số: Chuyển các hỗn số về dạng phân số để dễ thực hiện các phép tính (trừ, cộng, nhân, chia).

Thực hiện phép tính theo thứ tự:

Với phép tính có dấu ngoặc, thực hiện các phép trong ngoặc trước.

Thực hiện nhân, chia trước rồi mới cộng, trừ.

Rút gọn kết quả: Kết quả cuối cùng nếu là phân số thì rút gọn và chuyển về hỗn số nếu cần.

Lời giải:

a. $12 \frac{1}{3} - (3 \frac{3}{4} + 4 \frac{3}{4}) = \frac{37}{3} - (\frac{15}{4} + \frac{19}{4})$

$= \frac{37}{3} - \frac{34}{4} = \frac{23}{6}$

$b) 3 \frac{5}{6} + 2 \frac{1}{6} . 6 = \frac{23}{6} + 13 = \frac{101}{6}$

$c) 3 \frac{1}{2} + 4 \frac{5}{7} - 5 \frac{5}{14} = \frac{7}{2} + \frac{33}{7} - \frac{75}{14} = \frac{20}{7}$

d) $4 \frac{1}{2} + \frac{1}{2} : 5 \frac{1}{2}$

$= \frac{9}{2} + \frac{1}{2} : \frac{11}{2}$

$= \frac{9}{2} + \frac{1}{11}$

$= \frac{101}{22}$

Phương pháp chung

- Để tính giá trị biểu thức, ta căn cứ vào thứ tự thực hiện phép tính:

+ Biểu thức không có dấu ngoặc

• Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện theo thứ tự từ trái sang phải.

• Thực hiện theo thứ tự: Lũy thừa $\to$ Nhân, chia $\to$ Cộng, trừ.

+ Biểu thức có dấu ngoặc: trong ngoặc trước, ngoài ngoặc sau: ( ) $\to$ [] $\to$ {}.

- Sử dụng quy tắc cộng, trừ, nhân, chia số hữu tỉ dưới dạng phân số (hoặc số thập phân) kết hợp với các tính chất của các phép tính cộng và nhân để tính giá trị các biểu thức số hữu tỉ.

Câu 23: Biểu diễn A = $\sqrt{10 + \sqrt{24} + \sqrt{40} + \sqrt{60}}$ dưới dạng tổng của 3 căn thức

Phương pháp giải:

Biểu thức tổng dưới căn được viết lại thành dạng $a + 2\sqrt{bc}$ , với $a, b, c$ là các số nguyên.

Sử dụng các tích đặc biệt để tách biểu thức thành tổng của ba căn thức.

Nhận dạng biểu thức có dạng $(\sqrt{b} + \sqrt{c} + \sqrt{d})^2$ .

Rút gọn biểu thức để có kết quả dưới dạng tổng của ba căn thức.

Lời giải:

$A = \sqrt{10 + \sqrt{24} + \sqrt{40} + \sqrt{60}}$

$= \sqrt{10 + 2 \sqrt{6} + 2 \sqrt{10} + 2 \sqrt{15}}$

$= \sqrt{2 + 3 + 5 + 2 (\sqrt{2.3} + \sqrt{2.5} + \sqrt{3.5})}$

$= \sqrt{{(\sqrt{2} + \sqrt{3} + \sqrt{5})}^{2}}$

$= \sqrt{2} + \sqrt{3} + \sqrt{5}$

Câu 24: Số tập con là gì?

Công thức tính số tập con?

Phương pháp giải:

Nêu khái niệm và công thức tính tập con.

Lời giải:

+ Định nghĩa: Tập hợp con

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con (tập con) của B.

+ Kí hiệu

$A \subset B$ (đọc là A chứa trong B) hoặc $B \supset A$ (đọc là B chứa A).

+ Nhận xét:

· $A \subset A$ và $\emptyset \subset A$ với mọi tập A.

· Nếu A không là tập con của B thì ta viết $A ⊄ B$

· Nếu $A \subset B$ hoặc $A \subset B$ thì ta nói A và B có quan hệ bao hàm.

Công thức tinh số tập hợp con :

+) Tập hợp chính gồm n phần tử

Số tập hợp con gồm : 2ⁿ tập hợp

+) Ví dụ : Tập hợp A = { 1 ; 2; 3; 4 } gồm 4 phần tử nên số tập hợp con có là : 2⁴ = 16 (tập hợp)

+) Số tập hợp con là số tập hợp được lập mà mỗi tập hợp gồm các phần tử thuộc tập hợp chính.

Câu 25: Tìm x thuộc Z để x²+ 2x + 1 chia hết cho x + 6

Phương pháp giải:

Biến đổi phương trình về dạng có nhân tử chung là (x + 6).

Nhận xét và tìm x.

Lời giải:

$x^{2} + 2 x + 1 = x^{2} + 4 x - 4 x + 2 x + 1$

$x . (x + 6) - 4 x + 1$

$x . (x + 6) - 4 x - 24 + 25$

$x . (x + 6) - 4. (x + 6) + 25$

=> 25 chia hết cho x + 6.

Gọi $d = x + 6$ , tức là $x = d - 6$ .

Khi đó, ta thay vào $(x + 1)^2$ :

$(x + 1)^2 = ((d - 6) + 1)^2 = (d - 5)^2$ .

Để $(x + 1)^2$ chia hết cho $x + 6 = d$ , ta cần:

$d \mid (d - 5)^2$ . $d \mid (d - 5)^2$

$\Rightarrow d \mid d^2 - 10d + 25$ .

Vì $d \mid d^2$ , nên $d \mid -10d + 25$ .

$\Rightarrow d \mid 25$ . $d \in \{ \pm 1, \pm 5, \pm 25 \}$ .

Với $x = d - 6$ :

Nếu $d = 1$ , thì $x = 1 - 6 = -5$ .

Nếu $d = -1$ , thì $x = -1 - 6 = -7$ .

Nếu $d = 5$ , thì $x = 5 - 6 = -1$ .

Nếu $d = -5$ , thì $x = -5 - 6 = -11$ .

Nếu $d = 25$ , thì $x = 25 - 6 = 19$ .

Nếu $d = -25$ , thì $x = -25 - 6 = -31$

$x \in \{-31, -11, -7, -5, -1, 19\}.$

Câu 26: Đổi đơn vị:

3 năm rưỡi = ... tháng

3 ngày rưỡi = .. .giờ

Phương pháp giải:

1 năm = 12 tháng

1 ngày = 24 giờ

Lời giải:

1 năm = 12 tháng

nửa năm = 6 tháng

3 năm = 36 tháng

3 năm rưỡi = 3 năm + nửa năm

=> 3 năm rưỡi = 42 tháng

1 ngày = 24 giờ

nửa ngày = 12 giờ

3 ngày = 72 giờ

3 ngày rưỡi = 3 ngày + nửa ngày

=> 3 ngày rưỡi = 84 giờ

Câu 27: Tìm n thuộc Z sao cho

a) $\frac{n + 3}{n - 2}$ là âm

b) $\frac{n + 7}{3 n - 1}$ là số nguyên

c) $\frac{3 n + 2}{4 n - 5}$ thuộc N

Phương pháp giải:

a) $\frac{n+3}{n-2}$ là số âm:

Điều kiện để phân số âm là tử và mẫu trái dấu.

Xét từng trường hợp:

$n+3 > 0$ và $n-2 < 0$ , hoặc

$n+3 < 0$ và $n-2 > 0$ .

Giải bất phương trình tương ứng để tìm $n$ .

b) $\frac{n+7}{3n-1}$ là số nguyên:

Điều kiện: $n+7$ chia hết cho $3n-1$ .

Biến đổi:

$n+7 = k(3n-1)$ , với $k \in \mathbb{Z}$ .

Giải tìm $3n-1$ thuộc tập hợp các ước số của hằng số bên vế phải.

Lọc giá trị $n$ thuộc $\mathbb{Z}$ .

c) $\frac{3n+2}{4n-5} \in \mathbb{N}$

Điều kiện: $3n+2$ chia hết cho $4n-5$ .

Biến đổi:

$3n+2 = k(4n-5)$ , với $k \in \mathbb{N}$ .

Giải tìm $4n-5$ thuộc tập hợp các ước số của hằng số bên vế phải.

Lọc giá trị $n$ thuộc $\mathbb{Z}$ .

Lời giải:

a/ Để $\frac{n + 3}{n - 2}$ âm => $\frac{n + 3}{n - 2} < 0$

mà n - 2 < n + 3 => n - 2 < 0 => n < 2

Vậy n < 2 thì $\frac{n + 3}{n - 2}$ là số âm.

b/ Để $\frac{n + 7}{3 n - 1}$ nguyên => n + 7 chia hết cho 3n - 1

=> 3 (n + 7) chia hết cho 3n - 1

=> 3n + 21 chia hết cho 3n - 1

=> 22 chia hết cho 3n - 1

=> 3n - 1 ∈ Ư(22)

=> 3n - 1 ∈ { ±1 ; ±2 ; ±11 ; ±22 }

- Nếu 3n - 1 = 1 => 3n = 2 => n = 2/3 (ko thỏa mãn n ∈ Z)

- Nếu 3n - 1 = -1 => 3n = 0 => n = 0 (thỏa mãn)

- Nếu 3n - 1 = 2 => 3n = 3 => n = 1 (thỏa mãn)

- Nếu 3n - 1 = -2 => 3n = -1 => n = -1/3 (ko thỏa mãn n ∈ Z)

- Nếu 3n - 1 = 11 => 3n = 12 => n = 4 (thỏa mãn)

- Nếu 3n - 1 = -11 => 3n = -10 => n = -10/3 (ko thỏa mãn n ∈ Z)

- Nếu 3n - 1 = 22 => 3n = 23 => n = 23/3 (ko thỏa mãnn ∈ Z)

- Nếu 3n - 1 = -22 => 3n = -21 => n = -7 (thỏa mãn)

Vậy n ∈ { 0 ; 1 ; 4 ; -7 } thì $\frac{n + 7}{3 n - 1}$ là số nguyên.

c/ Để $\frac{3 n + 2}{4 n - 5} \in N$ => 3n + 2 chia hết cho 4n - 5

=> 4 (3n + 2) chia hết cho 4n - 5

=> 12n + 8 chia hết cho 4n - 5

=> 23 chia hết cho 4n - 5

=> 4n - 5 ∈ Ư(23)

=> 4n - 5 ∈ { 1 ; 23 }

- Nếu 4n - 5 = 1 => 4n = 6 => n = 3/2 (ko thoả mãn n ∈ Z)

- Nếu 4n - 5 = 23 => 4n = 28 => n = 7 (thỏa mãn)

Vậy n = 7 thì $\frac{3 n + 2}{4 n - 5} \in N$

Câu 28: Hai vòi nước cùng chảy vào 1 bể cạn thì sau 6 giờ sẽ đầy bể. Cùng chảy được 2 giờ thì khóa vòi một lại và vòi hai tiếp tục chảy thêm 12 giờ nữa thì đầy bể . Hỏi nếu mỗi vòi chảy riêng thì bao lâu mới đầy bể

Phương pháp giải:

Gọi thời gian chảy đầy bể của vòi 1 là $x$ và vòi 2 là $y$ .

Dùng hệ phương trình từ thông tin về thời gian hai vòi chảy cùng và chảy riêng để thiết lập các phương trình.

Giải hệ phương trình để tìm giá trị của $x$ và $y$ , từ đó xác định thời gian mỗi vòi chảy đầy bể.

Lời giải:

Gọi thời gian chảy 1 mình đầy bề của vòi 1 và vòi 2 lần lượt là x và y giờ (x; y > 0)

Trong 1 giờ hai vòi lần lượt chảy được $\frac{1}{x}$ và $\frac{1}{y}$ phần bể

Do 2 vòi cùng chảy trong 6h đầy bể nên: $\frac{1}{x} + \frac{1}{y} = \frac{1}{6}$

Hai vòi chảy 2h và khóa vòi 1, để vòi 2 chảy 12 giờ đầy bể nên: $2 (\frac{1}{x} + \frac{1}{y}) + 12. \frac{1}{y} = 1$

$\Rightarrow \frac{2}{x} + \frac{14}{y} = 1$

Ta được hệ: ${\begin{array}{c} \frac{1}{x} + \frac{1}{y} = \frac{1}{6} \\ \frac{2}{x} + \frac{14}{y} = 1 \end{array}$ $\Rightarrow {\begin{array}{c} \frac{1}{x} = \frac{1}{9} \\ \frac{1}{y} = \frac{1}{18} \end{array}$

$\Rightarrow {\begin{array}{c} x = 9 \\ y = 18 \end{array}$

Phương pháp chung

Trình tự các bước giải bài toán bằng cách lập hệ phương trình

• Bước 1: Lập hệ phương trình.

+ Biểu diễn hai đại lượng phù hợp bằng ẩn số x và y. Đặt đơn vị và điều kiện của ẩn.

+ Biểu thị các đại lượng chưa biết qua ẩn.

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng và thành lập hệ hai ẩn từ các phương trình vừa tìm.

• Bước 2: Giải hệ phương trình nói trên.

• Bước 3: Kiểm tra nghiệm tìm được thỏa mãn điều kiện của bài toán và nêu kết luận của bài toán.

Câu 29: Hiện nay tuổi cha gấp 3 lần tuổi con. Sau 1 thời gian nữa, khi tuổi của con bằng tuổi cha hiện nay thì lúc đó tổng số tuổi của 2 cha con là 112. tính tuổi của cha, của con hiện nay ?

Phương pháp giải:

Gọi ẩn số.

Xác định điều kiện sau một thời gian.

Lập và giải phương trình tổng tuổi.

Kết luận.

Lời giải:

Gọi x là tuổi con hiện nay $\Rightarrow$ 3x là tuổi cha

ta có

Tuổi con 1 thời gian sau = tuổi cha = 3x

=> 1 thời gian sau = 2x

Tuổi cha 1 thời gian sau = 3x + 2x = 5x

Ta có pt: 3x + 5x = 112 $\Rightarrow$ x = 14

$\Rightarrow$ Con 14 tuổi $\Rightarrow$ Cha = 14.3 = 42 tuổi

Câu 30: Chứng minh rằng: với hai số a, b thỏa mãn a > b > 0 thì $\sqrt{a} - \sqrt{b}$ < $\sqrt{a - b}$

Phương pháp giải:

Thiết lập bất đẳng thức cần chứng minh.

Bình phương hai vế để loại căn bậc hai.

Phát triển biểu thức và so sánh.

Lấy nhân tử chung và sử dụng tính chất $a > b$ để kết luận bất đẳng thức luôn đúng.

Lời giải:

$\sqrt[]{a} - \sqrt[]{b} < \sqrt[]{a - b} (a > b > 0)$

$\Leftrightarrow {(\sqrt[]{a} - \sqrt[]{b})}^{2} < {(\sqrt[]{a - b})}^{2}$

$\Leftrightarrow a + b - 2 \sqrt[]{a b} < a - b$

$\Leftrightarrow 2 \sqrt[]{a b} - 2 b > 0$

$\Leftrightarrow 2 \sqrt[]{b} (\sqrt[]{a} - \sqrt[]{b}) > 0 (1)$

mà $a > b > 0$

Nên $(1)$ luôn luôn đúng

Vậy $\sqrt[]{a} - \sqrt[]{b} < \sqrt[]{a - b}$

Câu 31: Mẹ mang ra chợ bán 25 quả cam và 75 quả quýt. Buổi sáng mẹ đã bán được một số cam và quýt, còn lại $\frac{1}{5}$ số cam và $\frac{1}{5}$ số quýt mẹ để chiều bán nốt. Hỏi buổi sáng mẹ đã bán được tổng số bao nhiêu quả cam và quýt?

Phương pháp giải:

Tính số cam và quýt còn lại sau buổi sáng bằng cách lấy $\frac{1}{5}$ số cam và quýt ban đầu.

Tính số cam và quýt đã bán buổi sáng bằng cách lấy tổng số ban đầu trừ đi số còn lại.

Cộng số cam và quýt đã bán để tìm tổng số quả đã bán buổi sáng.

Lời giải:

Số cam mẹ đã bán là:

25x (1 - $\frac{1}{5}$ ) = 20 (quả)

Số quýt mẹ đã bán là:

75x (1− $\frac{1}{5}$ ) = 60(quả)

Buổi sáng mẹ bán được:

60 + 20 = 80 (quả cam và quýt)

Đáp số: 80 quả cam và quýt

Câu 32: Hai sân bay Hà Nội và Đà Nẵng cách nhau 600km. Một máy bay cánh quạt từ Đà Nẵng đi Hà Nội. Sau đó 10 phút, một máy bay phản lực từ Hà Nội bay tới Đà Nẵng với vận tốc lớn hơn máy bay cánh quạt là 300km/h. Máy bay phản lực đến Đà Nẵng trước khi máy bay cánh quạt đến Hà Nội là 10 phút. Tính vận tốc mỗi máy bay.

Phương pháp giải:

Gọi $x$ là vận tốc máy bay cánh quạt (km/h), nên vận tốc máy bay phản lực là $x + 300$ (km/h).

Thiết lập và giải phương trình.

Kết luận.

Lời giải:

Gọi x là vận tốc máy bay cánh quạt, nên vận tốc máy bay phản lực: x + 300

Theo bài ta có phương trình:

$\frac{600}{x} - \frac{600}{x + 300} = 20' = \frac{1}{3} h$

$\begin{array}{l} \Rightarrow 600 x + 180000 - 600 x = \frac{1}{3} x^{2} + 100 x \\ \Leftrightarrow \frac{1}{3} x^{2} + 100 x - 180000 = 0 \Leftrightarrow [\begin{array}{l} x = 600 (t m) \\ x = - 900 (k t m) \end{array} \end{array}$

Vậy vận tốc máy bay cánh quạt: 600km/h, vận tốc máy bay phản lực 900km/h.

Câu 33: Tìm BCNN của:

a) 42; 70; 180.

b) 9; 10; 11

Phương pháp giải:

Viết dạng phân tích nguyên tố của từng số.

Lấy tất cả các thừa số nguyên tố xuất hiện trong mọi số.

Với mỗi thừa số nguyên tố, chọn số mũ lớn nhất xuất hiện trong các phân tích.

Nhân tất cả các thừa số đã chọn lại để tìm BCNN.

Lời giải:

a ) 42; 70; 180

42 = 2.3.7

70 = 2.5.7

180 = 2².3².5

BCNN (42,70,180) = 2².3².5.7 = 1260

b ) 9; 10; 11

9 = 3²

10 = 2.5

11 = 11

BCNN (9,10,11) = 3².2.5.11 = 990

Phương pháp chung

Tìm bội chung nhỏ nhất của hai hay nhiều số lớn hơn 1:

- Bước 1: Phân tích mỗi số ra thừa số nguyên tố;

- Bước 2: Chọn ra các thừa số nguyên tố chung và riêng;

- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN phải tìm.

* Chú ý:

- Nếu $a ⋮ b$ thì BCNN (a, b) = a.

- BCNN (a, 1) = a; BCNN (a, b, 1) = BCNN (a, b).

Câu 34: Đổi đơn vị sau:

38m² 25dm² = ....dm²

15dm² 9cm² = ...cm²

198cm² = ..dm²...cm²

2080dm² = ..m²..dm²

3107m² = ..dam²..m²

Phương pháp giải:

Nhớ các mối quan hệ giữa các đơn vị:

$1 \, m^2 = 100 \, dm^2$ .

$1 \, dm^2 = 100 \, cm^2$ .

Quy đổi về đơn vị nhỏ hơn hoặc lớn hơn:

Khi đổi sang đơn vị nhỏ hơn, nhân với hệ số tương ứng.

Khi đổi sang đơn vị lớn hơn, chia cho hệ số tương ứng (lấy phần nguyên và phần dư nếu có).

Lời giải:

38m² 25dm² = 3825 dm²

$15 d m^{2} 9 c m^{2} = 1509 c m^{2}$

$198 c m^{2} = 1 d m^{2} 98 c m^{2}$

$2080 d m^{2} = 20 m^{2} 80 d m^{2}$

$3107 m^{2} = 31 d a m^{2} 7 m^{2}$

Câu 35: Con gà mái của bạn An sau 2 tuần 1 ngày đã đẻ được 1 số trứng. Bạn An tính rằng cứ 3 ngày nó đẻ được 2 quả trứng. Hỏi con gà đó đã đẻ được mấy quả trứng?

Phương pháp giải:

Chuyển đổi thời gian:

1 tuần = 7 ngày

Tính số chu kỳ 3 ngày trong 15 ngày.

Tính tổng số trứng.

Lời giải:

2 tuần 1 ngày = 15 ngày

3 ngày đẻ 2 quả thì 15 ngày đẻ được:

15 : 3 x 2 = 10 (quả)

Đáp số: 10 quả trứng

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

139

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm