Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 24)

Câu 1: Thực hiện phép tính: 333 : 3 + 225 : 15², rồi phân tích kết quả ra thừa số nguyên tố.

Lời giải:

333 : 3 + 225 : 15²

= 333 : 3 + 225 : 225

= 111 + 1 = 112

Phân tích số 112 thành tích các thừa số nguyên tố là:

112 = 2⁴ × 7.

Câu 2: Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Lời giải:

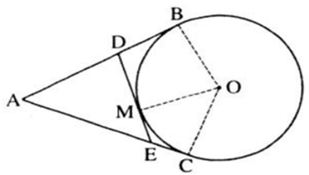
Vì AB, AC là hai tiếp tuyến của (O) lần lượt tại B và C.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: AB = AC

Vì DB, DM là hai tiếp tuyến của (O) lần lượt tại B và M.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: DB = DM

Vì EM, EC là hai tiếp tuyến của (O) lần lượt tại M và C.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: EM = EC

Chu vi tam giác ADE là:

AD + DE + EA

= AD + (DM + ME) + EA

= (AD + DM) + (ME + EA)

= (AD + DB) + (EC + EA) (do DB = DM, EM = EC)

= AB + AC = 2AB (do AB = AC).

Câu 3: Phân tích đa thức 4x² − 12x + 9 thành nhân tử.

Lời giải:

4x² − 12x + 9

= (2x)² − 2.2x.3 + 3²

= (2x + 3)²

Câu 4: Tìm x, biết: 4x² − 12x = −9.

Lời giải:

4x² − 12x = −9

4x² − 12x + 9 = 0

(2x)² − 2.2x.3 + 3² = 0

(2x + 3)² = 0

2x + 3 = 0

$\iff x=-\frac{3}{2}$.

Câu 5: Chứng minh a, b, c là độ dài 3 cạnh của một tam giác thì

(b + c − a)(c + a − b)(a + b − c) $\le$ abc.

Lời giải:

Ta có: 

(b + c − a)(c + a − b) = c² − (a − b)² ≤ c²

(c + a − b)(a + b − c) = a² − (b − c)² ≤ a²

(a + b − c)(b + c − a) = b² − (c − a)² ≤ b²

Nhân vế với vế của các bđt trên với chú ý a + b − c > 0; b + c − a > 0; c + a − b > 0 ta có:

[(a + b − c)(b + c − a)(c + a − b)]² ≤ (abc)²

(b + c − a)(c + a − b)(a + b − c) $\le$ abc

Đẳng thức xảy ra khi và chỉ khi a = b = c.

Câu 6: Chứng tỏ rằng: 2x + 3y chia hết cho 17 thì 9x + 5y chia hết cho 17.

Lời giải:

Ta có: 2x + 3y chia hết cho 17

4(2x + 3y) ⋮ 17

8x + 12y ⋮ 17

Mà ta có:

8x + 12y + 9x + 5y = 17x + 17y ⋮ 17

Vậy 9x + 5y ⋮ 17

Câu 7: Xe thứ nhất chở 4,25 tấn hàng. Xe thứ nhất chở ít hơn xe thứ hai 130 yến và nhiều hơn xe thứ ba 7 tạ. Hỏi cả ba xe chở bao nhiêu tấn hàng?

Lời giải:

Đổi: 4,25 tấn = 425 yến; 7 tạ = 70 yến

Xe 2 chở được số tấn hàng là:

425 + 130 = 555 (yến)

Xe 3 chở được số tấn hàng là:

425 − 70 = 355 (yến)

Cả 3 xe chở được số tấn hàng là:

425 + 555 + 355 = 1335(yến)

Đổi: 1335 yến = 13,55 tấn

Đáp số: 13,55 tấn.

Câu 8: Xe thứ nhất chở 4,25 tấn hàng. Xe thứ nhất chở ít hơn xe thứ hai 130 yến  và nhiều hơn xe thứ ba 3 tạ. Hỏi xe thứ hai chở bao nhiêu tấn hàng?

Lời giải:

Đổi: 130 yến = 1,3 tấn

Xe thứ hai chở số tấn hàng là:

4,25 + 1,3 = 5,55 (tấn)

Đáp số: 5,55 tấn hàng.

Câu 9: Tìm các giá trị thích hợp của a và b.

a) a00 > −111;

b) −a99 > −600;

c) −cb3 < −cba;

d) −cab < −c85.

Lời giải:

a) a00 > −111

Vậy các giá trị của a thỏa mãn là a $\in$ {1; 2; 3; …; 9}.

b) −a99 > −600

Vậy các giá trị của a thỏa mãn là a $\in$ {1; 2; 3; 4; 5}.

c) −cb3 < −cba

Vậy các giá trị của a thỏa mãn là a $\in$ {1; 2}.

Các giá trị của b thỏa mãn là b $\in$ {0; 1; 2; 3; …; 9}

Các giá trị của của c thỏa mãn là c $\in$ {1; 2; 3; …; 9}.

d) −cab < −c85

Vậy các giá trị của ab thỏa mãn là ab $\in$ {86; 87; 88; …; 99}

Các giá trị của của c thỏa mãn là c $\in$ {1; 2; 3; …; 9}.

Câu 10: Một trường tổ chức cho khoảng từ 700 đến 800 học sinh đi tham quan bằng ô tô. Tính số học sinh đi tham quan, biết rằng nếu xếp 40 học sinh hay 45 học sinh vào một xe thì vừa đủ.

Lời giải:

Gọi a (học sinh) là số học sinh của trường đó.

Vì a chia hết cho cả 40 và 45 nên a Î BC(40, 45).

Ta có 40 = 2³.5; 45 = 3².5

$\Rightarrow$ BCNN(40, 45) = 2³.3².5 = 360

$\Rightarrow$ a $\in$ BC(40, 45) = B(360) = {0; 360; 720; 1080; ...}.

mà 700 ≤ a ≤ 800 nên a = 720.

Vậy số học sinh là 720 học sinh.

Câu 11: Một trường tổ chức cho khoảng từ 700 đến 800 học sinh đi tham quan bằng ô tô. Tính số học sinh đi tham quan, biết rằng nếu xếp 40 người hay 45 người lên một xe đều vừa vặn. Nếu xếp 40 người thì cần bao nhiêu xe?

Lời giải:

Gọi a (học sinh) là số học sinh của trường đó.

Vì a chia hết cho cả 40 và 45 nên a Î BC(40, 45).

Ta có 40 = 2³.5; 45 = 3².5

$\Rightarrow$ BCNN(40, 45) = 2³.3².5 = 360

$\Rightarrow$ a $\in$ BC(40, 45) = B(360) = {0; 360; 720; 1080; ...}

mà 700 ≤ a ≤ 800 nên a = 720.

Do đó trường đó có 720 học sinh.

Vậy để xếp 40 người 1 xe thì cần số xe là: 

720 : 40 = 18 (xe).

Câu 12: Tìm 1 số biết rằng nếu giảm số đó đi 6 lần rồi thêm vào 25,71 thì được 88,5.

Lời giải:

Số cần tìm là:

(88,5 − 25,71) × 6 = 376,74

Đáp số: 376,74.

Câu 13: Chứng minh rằng tích của 4 số tự nhiên liên tiếp chia hết cho 24.

Lời giải:

Gọi 4 số tự nhiên liên tiếp là x; x + 1; x + 2; x + 3

 Ta có tích 4 số đó là x(x + 1)(x + 2)(x + 3).

Vì x(x+1) là tích 2 số liên tiếp nên chia hết cho 2

x(x+1)(x+2) là tích 3 số liên tiếp nên chia hết cho 3

x(x+1)(x+2)(x+3) là tích 4 số liên tiếp nên chia hết cho 4.

Mà 2.3.4 = 24 Þ x(x+1)(x+2)(x+3) là bội của 24.

Hay x(x+1)(x+2)(x+3) chia hết cho 24.

Câu 14: Ông Hùng mua 300 viên gạch hình vuông cạnh 30 cm để lật lên 1 phòng khách và 1 phòng ngủ thì vừa hết. Hỏi diện tích phòng khách nhà ông Hùng có diện tích bao nhiêu m². Biết phòng ngủ có diện tích 9 m² và diện tích mạch vùng không đáng kể.

Lời giải:

Đổi: 9m² = 90 000 cm².

Diện tích của một viên gạch là:

30 × 30 = 900 (viên)

Vậy để lát hết phòng ngủ cần số viên gạch là:

90 000 : 90 = 100 (viên)

Số viên gạch dùng để lát phòng khách là:

300 − 100 = 200 (viên)

Diện tích của phòng khách là:

200 × 900 = 180 000 (cm²) = 18 (m²)

Đáp số: 18 m².

Câu 15: Tìm ƯCLN của:

a) 35 và 105;

b) 15; 180 và 165.

Lời giải:

a) Vì 105 ⋮ 35 nên ƯCLN(35, 105) = 35.

Vậy ƯCLN(35, 105) = 35.

b) Vì 180 ⋮ 15; 165 ⋮ 15 nên ƯCLN(15, 180, 165) = 15.

Vậy ƯCLN(15, 180, 165) = 15.

Câu 16: Cho góc nhọn a, biết sin a = 0,6. Không tính số đo góc a, hãy tính cos a, tan a, cot a.

Lời giải:

Ta có ${\sin }^2\alpha +{\cos }^2\alpha =1\Rightarrow {\cos }^2\alpha =1-{\mathrm{0,6}}^2=\mathrm{0,64}$ .

Vì  a là góc nhọn nên suy ra cos a = 0,8.

• $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{\mathrm{0,6}}{\mathrm{0,8}}=\frac{3}{4}$ ;

• $\cot \alpha =\frac{1}{\tan \alpha }=\frac{4}{3}$ .

Câu 17: Tìm số tự nhiên x, biết:

52 − (2x + 32) + 42 : 7 = 6.

Lời giải:

52 − (2x + 32) + 42 : 7 = 6

52 − (2x + 32) + 6 = 6

52 − (2x + 32) = 6 − 6

52 − (2x + 32) = 0

(2x + 32) = 52 − 0

2x + 32 = 52

2x = 20 

x = 20 : 2

Vậy x = 10 

Câu 18: Tìm số tự nhiên x, biết:

42 − (2x + 32) + 12 : 2 = 6

Lời giải:

42 − (2x + 32) + 12 : 2 = 6

42 − (2x + 32) + 6 = 6

42 − (2x + 32) = 6 − 6

42 − (2x + 32) = 0

(2x + 32) = 42 − 0

2x + 32 = 42

2x = 10 

x = 10 : 2

Vậy x = 5 

Câu 19: Chú Tư thả cá trong khu đầm hình thoi có chu vi là 2 km, đường chéo nhỏ bằng $\frac{3}{4}$  đường chéo lớn và $\frac{6}{5}$  cạnh của hình thoi. Trung bình cứ 1 ha đầm thu được 15 tấn cá. Hỏi chú Tư thu hoạch được bao nhiêu tấn cá?

Lời giải:

Chiều dài cạnh khu đầm là:

2 : 4 = 0,5 (km)

Chiều dài đường chéo nhỏ khu đầm là:

0,5 × 6 : 5 = 0,6 (km)

Chiều dài đường chéo lớn khu đầm:

0,6 : 3 × 4 = 0,8 (km)

Diện tích khu đầm:

0,6 × 0,8 : 2 = 0,24 (km²) = 24 (ha)

Chú Tư hoạch được số tấn cá là:

24 : 1 × 15 = 360 (tấn)

Đáp số: 360 tấn.

Câu 20: Tìm ước chung của 18 và 24

Lời giải:

• Ư(18) = {1; 2; 3; 6; 9; 18}.

• Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.

Vậy ƯC(18, 24) = {1; 2; 3; 6 }

Câu 21: ƯCLN(18, 24) là:

Lời giải:

18 = 2.3²; 24 = 2³.3

$\Rightarrow$ ƯCLN(18, 24) = 2.3 = 6.

Câu 22: Tìm GTNN: A = x² − 2xy + 2y² + 2x − 10y +17.

Lời giải:

A = x² − 2xy + 2y² + 2x − 10y +17

= (x² − 2xy + y²) + 2(x − y) + 1 + (y² − 8y +16)

= (x − y)² + 2(x − y) + 1 + (y − 4)²

= (x − y + 1)² + (y − 4)² ≥ 0.

Vậy GTNN của A bằng 0 khi $\left\{\begin{array}{l}x-y+1=0\\ y-4=0\end{array}\right.\iff \left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ .

Câu 23: Chứng minh rằng với mọi a thuộc ℤ, ta có:

(a − 1)(a + 2) + 12 không là bội của 9.

Lời giải:

• TH1: a = 3k (k $\in$ ℤ)

Ta có: (a − 1)(a + 2) + 12 = (3k − 1)(3k + 2) + 12

Vì (3k − 1)(3k + 2) không chia hết cho 3 mà 12 chia hết cho 3.

Nên suy ra: (3k − 1)(3k + 2) + 12 không chia hết cho 3.

Do đó (3k − 1)(3k + 2) + 12 không chia hết cho 9.

• TH2: a = 3k + 1 (k $\in$ ℤ)

Ta có: (a − 1)(a + 2) + 12 = 3k(3k + 3) + 12 = 9k(k + 1) + 12

Vì 9k(k + 1) chia hết cho 9 mà 12 không chia hết cho 9.

Do đó 9k(k + 1) + 12 không chia hết cho 9.

• TH3: a = 3k + 2 (k $\in$ ℤ)

Ta có: (a − 1)(a + 2) + 12 = (3k + 1)(3k + 4) + 12

Vì (3k + 1)(3k + 4) + 12 không chia hết cho 3 mà 12 chia hết cho 3.

Nên suy ra: (3k + 1)(3k + 4) + 12 không chia hết cho 3.

Do đó (3k + 1)(3k + 4) + 12 không chia hết cho 9.

Vậy suy ra với mọi a thuộc ℤ, ta có: (a − 1)(a + 2) + 12 không là bội của 9.

Câu 24: So sánh 2³⁰⁰ và 3²⁰⁰.

Lời giải:

Ta có: $2^{300}={\left(2^3\right)}^{100}=8^{100}$ ;

$3^{200}={\left(3^2\right)}^{100}=9^{100}$.

Vì $8<9\Rightarrow 8^{100}<9^{100}$ .

Vậy: 2³⁰⁰ < 3²⁰⁰.

Câu 25: Theo cách tính của bạn Nam, hãy viết số thích hợp vào chỗ chấm để tìm 32,5 % của 360.

……… của 360 là ………

……… của 360 là ………

……… của 360 là ………

……… của 360 là ………

……… của 360 là ………

Lời giải:

10% của 360 là 36

20% của 360 là 72

5% của 360 là 18

2,5% của 360 là 9

32,5% của 360 là 117

Câu 26: 15 % của 360 lít là:

Lời giải:

15 % của 360 lít là:

360 × 15 % = 54 (lít)

Đáp số: 54 lít.

Câu 27: (x + 3).(x + y − 5) = 7. Tìm cặp số x, y.

Lời giải:

(x + 3).(x + y − 5) = 7

$\Rightarrow$ (x + 3), (x + y − 5) $\in$ Ư(7) = {−1; 1; 7; −7}.

Lập bảng tìm x, y:

Vậy các cặp số (x; y) thỏa mãn là: (x; y) $\in$ {(−10; 14); (−4; 2); (−2; 14); (4; 2)}.

Câu 28: Tìm các số nguyên x,y sao cho (x − 3)(y − 5) = 7.

Lời giải:

(x − 3)(y − 5) = 7

$\Rightarrow$ (x − 3), (y − 5) $\in$ Ư(7) = {−1; 1; 7; −7}.

Lập bảng tìm x, y:

Vậy các cặp số (x; y) thỏa mãn là: (x; y) $\in$ {(−4; 4); (2; −2); (4; 11); (10; 6)}.

Câu 29: Để viết các số tự nhiên liên tiếp từ 2 đến 125 thì cần dùng bao nhiêu chữ số?

Lời giải:

Từ 2 đến 9 có số chữ số là:

(9 − 2) : 1 + 1 = 8 (số)

Để viết từ 2 đến 9 cần số chữ số là:

8 × 1 = 8 (chữ số)

Từ 10 đến 99 có số chữ số là:

(99 − 10) : 1 + 1 = 90 (số)

Để viết từ 10 đến 99 cần số chữ số là:

90 × 2 = 180 (chữ số)

Từ 100 đến 125 có số chữ số là:

(125 − 100) : 1 + 1 = 26 (số)

Để viết từ 2 đến 9 cần số chữ số là:

26 × 3 = 78 (chữ số)

Vậy để viết các số tự nhiên liên tiếp từ 2 đến 125 thì cần dùng số chữ số là:

8 + 180 + 78 = 266 (chữ số)

Đáp số: 266 chữ số.

Câu 30: Thu gọn đa thức x³ – 5y² + x + x³ – y² – x, ta được

A. x⁶ – 6y²;

B. x⁶ – 4y⁴;

C. 2x³ – 6y²;

D. 2x³ – 4y².

Lời giải:

Đáp án đúng là: C

Ta có x³ – 5y² + x + x³ – y² – x

= (x³ + x³) + (-5y² – y²) + (x – x)

= 2x³ – 6y².

Câu 31: Một tổ công nhân có 12 người. Cần chọn 3 người làm tổ trưởng, tổ phó, thành viên. Hỏi có bao nhiêu cách chọn?

A. 1230;

B. 12!;

C. 220;

D. 1320.

Lời giải:

Số cách chọn 3 người làm tổ trưởng , tổ phó và thanh viên là một chỉnh hợp chập 3 của 12 phần tử:

$A_{12}^3=1320$ (cách).

Câu 32: Một người có 0,23 tấn gạo. Lần đầu người đó bán được $\frac{1}{10}$ số gạo, lần sau bán được $\frac{1}{3}$ số gạo còn lại. Hỏi sau hai lần bán người đó còn lại bao nhiêu tấn gạo?

Lời giải:

Lần đầu người đó bán được số tấn gạo là:

$\mathrm{0,23.}\frac{1}{10}=\mathrm{0,023}$ (tấn)

Lần sau người đó bán số tấn gạo là:

$\left(\mathrm{0,23}-\mathrm{0,023}\right).\frac{1}{3}=\mathrm{0,069}$ (tấn)

Sau hai lần bán người đó còn lại số tấn gạo là:

0,23 – 0,023 – 0,069 = 0,138 (tấn)

Đáp số : 0,138 tấn gạo.

Câu 33: Xét đa thức p(n) = n² – n + 41. Hãy tính p(1), p(2), p(3), p(4), p(5) và chứng tỏ các kết quả nhận được đều là các số nguyên tố.

Lời giải:

Ta có: p(1) = 1² – 1 + 41 = 41;

p(2) = 2² – 2 + 41 = 43;

p(3) = 3² – 3 + 41 = 47;

p(4) = 4² – 4 + 41 = 53;

p(5) = 5² – 5 + 41 = 61.

Các số 41; 43. 47; 53; 61 đều là các số nguyên tố.

Suy ra p(1), p(2), p(3), p(4), p(5) cũng đều là các số nguyên tố.

Câu 34: Tìm một số tự nhiên biết, nếu xóa chữ số 0 ở hàng đơn vị của nó đi ta được số mới kém số phải tìm là 1818 đơn vị.

Lời giải:

Nếu xóa chữ số 0 ở hàng đơn vị của số đó ta được số mới kém số phải tìm 10 lần.

Gọi A là số cần tìm. B là số khi số A bị xóa số 0 hàng đơn vị.

Ta có sơ đồ:

 

Theo sơ đồ, hiệu số phần bằng nhau là:

10 – 9 = 1 (phần)

Số cần tìm là:

1818 : 1 ´ 10 = 2020.

Đáp số: 2020.

Câu 35: Một mảnh đất hình chữ nhật có chu vi 320 m, chiều dài hơn chiều rộng 30 m. Tìm chiều dài của mảnh đất?

Lời giải:

Nửa chu vi mảnh đất hình chữ nhật là:

320 : 2 = 160 (m)

Chiều dài của mảnh đất hình chữ nhật là:

(160 + 30) : 2 = 95 (m)

Đáp số: 95 m.

Câu 36: Một mảnh đất hình chữ nhật có nửa chu vi là 30 m và chiều dài hơn chiều rộng 60 dm. Tính diện tích mảnh đất.

Lời giải:

Đổi: 30 m = 300 dm.

Ta có chiều dài của mảnh đất là:

(300 + 60) : 2 = 180 (dm)

Chiều rộng của mảnh đất là:

180 – 60 = 120 (dm)

Diện tích của mảnh đất là:

180 . 120 = 21 600 (dm²)

Đáp số: 21 600 dm².

Câu 37: Một đội y tế có 24 bác sĩ và 108 y tá. Có thể chia đội y tế đó nhiều nhất thành mấy tổ để số bác sĩ và y tá được chia đều cho các tổ?

Lời giải:

Gọi a (tổ) là số tổ cần chia (a ∈ ℕ*).

Vì 24 chia hết cho a suy ra a ∈ Ư(24) và a lớn nhất.

Vì 108 chia hết cho a suy  a ∈ Ư(108) và a lớn nhất.

Do đó a là ƯCLN (24, 108).

Ta có:

• Ư(108) = {1; 2; 3; 4; 6; 9; 12; 18; 27; 36; 108}

• Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}

Do đó ƯCLN(24, 108) = 12.

Vậy có thể chia được nhiều nhất 12 tổ.

Vậy có thể chia đội y tế đó nhiều nhất thành 12 tổ để số bác sĩ và y tá được chia đều cho các tổ.

Câu 38: Rô-bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để Rô-bốt lấy được 100 ml nước từ chậu nước?

Lời giải:

Ta có: 250 ´ 2 – 400 = 100.

Vậy đổ 2 cốc 250 ml nước vào cốc 400 ml thì còn dư lại 100 ml nước trong cốc 250 ml.

Câu 39: So sánh 3⁹⁹ và 11²¹.

Lời giải:

Ta có: 3⁹⁹ = (3³³)³ = [(3³)¹¹]³ = (27¹¹)³.

Lại có: 11²¹ = (11⁷)³

Vì 27¹¹ > 27⁷ > 11⁷

Suy ra: 27¹¹ > 11⁷

Do đó (27¹¹)³ > (11⁷)³

Vậy 3⁹⁹ > 11²¹.

Câu 40: Một đơn vị thanh niên xung phong chuẩn bị một số gạo đủ cho đơn vị ăn trong 30 ngày. Sau 10 ngày đơn vị nhận thêm 10 người nữa. Hỏi số gạo còn lại đó đơn vị sẽ đủ ăn trong bao nhiêu ngày (biết lúc đầu đơn vị có 90 người)?

Lời giải:

Số suất ăn chuẩn bị cho 90 người trong 30 ngày là:

30 x 90 = 2 700 (suất)

Số suất ăn dành cho 90 người trong 10 ngày là:

10 x 90 = 900 (suất)

Số suất ăn còn lại là:

2700 – 900  = 1800 (suất)

Số người sau khi đến thêm là:

90 + 10 = 100 (người)

Số suất ăn còn lại đủ cho 100 người trong số ngày là:

1800 : 100 = 18 (ngày)

Đáp số: 18 ngày.

Câu 41: Cho a, b, c là ba số thực đôi một khác nhau thỏa mãn:

a² + b = b² + c = c² + a. Tính T = (a + b – 1)(b + c – 1)(c + a – 1).

Lời giải:

Theo bài cho ta có:

$\left\{\begin{array}{l}{a}^2-b^2=c-b\\ b^2-c^2=a-c\\ c^2-a^2=b-c\end{array}\right.\Rightarrow \left\{\begin{array}{l}a+b=\frac{c-b}{a-b}\\ b+c=\frac{a-c}{b-c}\\ c+a=\frac{b-a}{c-a}\end{array}\right.$ (do a ≠ b ≠ c)

$\Rightarrow \left\{\begin{array}{l}a+b-1=\frac{c-a}{a-b}\\ b+c-1=\frac{a-b}{b-c}\\ c+a-1=\frac{b-c}{c-a}\end{array}\right.$

$\Rightarrow$ T = (a + b – 1)(b + c – 1)(c + a – 1)

= $\frac{\left(c-a\right)\left(a-b\right)\left(b-c\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=1$

Câu 42: Tìm x đề (x + 17) chia hết cho (x + 3).

Lời giải:

Ta có: x + 17 = (x + 3) + 14

Để $\left(x+17\right)⋮\left(x+3\right)$ mà $14⋮\left(x+3\right)$

Do đó (x + 3) ∈ Ư(14).

Ta có Ư(14) = {−14; −7; −2;−1; 1; 2; 7; 14}.

Vậy x ∈ {−17; −10; −5; −4; −2; −1; 4; 11}.

Câu 43: Một đội công nhân có 63 người nhận sửa xong 1 quãng đường trong 11 ngày, Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa ?

Lời giải:

Một người sửa hết quãng đường đó trong số ngày là:

63 x 11 = 693 (ngày)

Muốn sửa quãng đường đó trong 7 ngày thì cần số người là:

693 : 7 = 99 (người)

Muốn sửa quãng đường đó trong 7 ngày thì cần thêm số người là:

99 – 63 = 36  (người)

Đáp số: 36 người.

Câu 44: Tìm ba số x, y, z biết x : y : z = 3 : 5 : 7 và x – y + z = 35.

Lời giải:

Từ x : y : z = 3 : 5 : 7 $\Rightarrow \frac{x}{3}=\frac{y}{5}=\frac{z}{7}$.

Theo tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x-y+z}{3-5+7}=\frac{35}{5}=7$

Suy ra x = 7. 3 = 21; y = 7. 5 = 35; z = 7. 7 = 49.

Vậy x = 21; y = 35 và z = 49.

Câu 45: Tìm x, y, z biết x : y : z = 3 : 5 : (−2) và 5x – y + 3z = −16.

Lời giải:

Ta có: x : y : z = 3 : 5 : (−2) $\Rightarrow \frac{x}{3}=\frac{y}{5}=\frac{z}{-2}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{x}{3}=\frac{y}{5}=\frac{z}{-2}=\frac{5x-y+3z}{5.3-5+3.(-2)}=\frac{-16}{4}=-4$.

Suy ra: x = 3.(−4) = −12; y = 5.( −4) = −20; z = (−4).( −2) = 8.

Vậy x = −12; y = −20; z = 8.

Câu 46: Số thứ nhất hơn số thứ hai là 223. Biết rằng nếu lấy số thứ nhất cộng với số thứ hai rồi cộng với tổng của chúng thì được 6 386. Tìm hai số đó.

Lời giải:

Tổng của hai số đó là:

6386 : 2 = 3193.

Số lớn là: (223 + 3193) : 2 = 1708.

Số bé là: 1708 – 223 = 1485.

Đáp số: Số lớn: 1708;

Số bé: 1485.

Câu 47: Số thứ nhất hơn số thứ hai là 115. Biết rằng nếu lấy số thứ nhất cộng với số thứ hai rồi cộng với tổng của chúng thì được 2 246. Tìm hai số đó.

Lời giải:

Tổng của hai số đó là:

2246 : 2 = 1123.

Khi đó ta có số lớn là:

(115 + 1123) : 2 = 619.

Số bé là: 619 – 115 = 504.

Đáp số: Số lớn: 619;

Số bé: 504.

Câu 48: Có 9 ô tô chuyển thực phẩm vào thành phố, trong đó 5 ô tô đi đầu, mỗi ô tô chuyển được 36 tạ và 4 ô tô đi sau, mỗi ô tô chuyển được 45 tạ. Hỏi trung bình mỗi ô tô chuyển được bao nhiêu tấn thực phẩm?

Lời giải:

5 ô tô đầu chở được số thực phẩm là:

36 × 5 = 180 (tạ) 

4 ô tô sau chở được số thực phẩm là:

45 × 4 = 180 (tạ)

Trung bình mỗi xe chuyển được số thực phẩm là:

(180 + 180) : (5 + 4) = 40 (tạ) = 4 (tấn) 

Đáp số: 4 tấn.

Câu 49: Một ô tô đi trong 2 giờ đầu, mỗi giờ đi được 55,5 km. Trong 3 giờ sau, mỗi giờ đi được 60,5 km. Hỏi trung bình mỗi giờ ô tô đi được bao nhiêu km?

Lời giải:

2 giờ đầu ô tô đi được là:

55,5 x 2 = 111 (km)

3 giờ sau ô tô đi được là:

60,5 x 3 = 181,5 (km)

Tổng số giờ ô tô đi là: 2 + 3 = 5 (giờ)

Vậy trung bình 1 giờ ô tô đi được là:

(111 + 181,5) : 5 = 58,5 (km)

Đáp số: 58,5 km.

Câu 50: Một ô tô trong 2 giờ đầu mỗi giờ đi được 55,6 km trong 3 giờ sau mỗi giờ đi được 46,5 km. Hỏi trung bình mỗi giờ ô tô đó đi được bao nhiêu km?

Lời giải:

2 giờ đầu ô tô đi được là:

55,6 x 2 = 111,2 (km)

3 giờ sau ô tô đi được là:

46,5 x 3 = 139,5 (km)

Tổng số giờ ô tô đi là: 2 + 3 = 5 (giờ)

Trung bình 1 giờ ô tô đi được là:

(111,2 + 139,5) : 5 = 50,14 (km)

Đáp số: 50,14 km.