Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Dạng toán tính nhanh lớp 5 và bài tập vận dụng chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết về phương pháp tính nhanh, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Tam giác đều
1. Định nghĩa tam giác đều
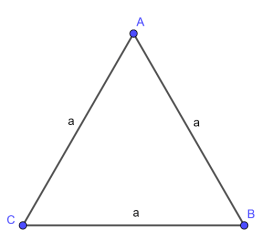
Tam giác đều là tam giác có ba cạnh bằng nhau.
Tam giác ABC đều có AB = AC = BC.
2. Tính chất tam giác đều
• Trong một tam giác đều, mỗi góc bằng 600.
Tam giác ABC đều
• Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
Nếu 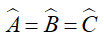
• Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
Tam giác ABC cân tại A. Nếu ta có 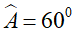
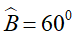
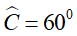
• Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó.
Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD là đường cao và đường phân giác của tam giác ABC.
3. Dấu hiệu nhận biết tam giác đều
• Tam giác có ba cạnh bằng nhau là tam giác đều
• Tam giác có ba góc bằng nhau là tam giác đều
• Tam giác cân có một góc bằng 600 là tam giác đều
• Tam giác có hai góc bằng 600 là tam giác đều
4. Cách vẽ tam giác đều ABC khi biết độ dài một cạnh bằng a
Bước 1: Vẽ đoạn thẳng .
![]()
Bước 2: Dùng ê ke có góc , vẽ góc bằng .
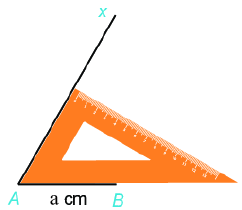
Bước 3: Vẽ góc hai tia cắt nhau tại , ta được tam giác đều .
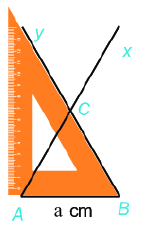
5. Chu vi tam giác đều
Trong đó, P là chu vi tam giác; a là độ dài ba cạnh của tam giác đó.
6. Diện tích tam giác đều
Vì tam giác ABC đều nên đường cao kẻ từ đỉnh A trùng với đường trung tuyến kẻ đỉnh A của tam giác ABC
Diện tích tam giác ABC là:
7. Bài tập về tam giác đều
Bài 1. Cho hình vẽ bên.
Hỏi tam giác nào là tam giác cân, tam giác nào là tam giác đều?
Hướng dẫn giải:
+ Xét ∆ABC, có: AB = BC = 2 cm.
Do đó ∆ABC cân tại B.
+ Xét ∆DEF, có: .
Do đó ∆DEF là tam giác đều.
+ Xét ∆MNP, có: MN = MP và
Do đó ∆MNP là tam giác đều.
+ ∆XYZ vuông tại X: .
Suy ra
Do đó .
Suy ra ∆XYZ cân tại X.
(Vì ∆XYZ cân tại X và có , do đó ta gọi ∆XYZ là tam giác vuông cân tại X).
Vậy ở hình bên, ta có:
- Các tam giác cân là: ∆ABC (cân tại B) và ∆XYZ (vuông cân tại X).
- Các tam giác đều là: ∆DEF và ∆MNP.
Bài 2. Cho ba điểm A, B, C thẳng hàng theo thứ tự đó. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều ACD, BCE. Gọi I, K theo thứ tự là trung điểm của AE và BD. Chứng minh rằng ∆CIK là tam giác đều.
Hướng dẫn giải:
Ta có ∆ACD đều. Suy ra (1).
Ta có ∆BCE đều. Suy ra (2).
Từ (1), (2), ta suy ra .
Do đó
Khi đó ta có
Xét ∆ACE và ∆DCB, có:
AC = DC (∆ACD đều).
(chứng minh trên).
CE = CB (∆BCE đều).
Do đó ∆ACE = ∆DCB (cạnh – góc – cạnh).
Suy ra và AE = DB (cặp góc và cặp cạnh tương ứng).
Vì I là trung điểm AE nên ta có AE = 2AI.
Vì K là trung điểm DB nên ta có DB = 2DK.
Mà AE = DB (chứng minh trên).
Do đó 2AI = 2DK.
Suy ra AI = DK.
Xét ∆ACI và ∆DCK, có:
AC = DC (∆ACD đều).
(chứng minh trên).
AI = DK (chứng minh trên).
Do đó ∆ACI = ∆DCK (cạnh – góc – cạnh).
Suy ra CI = CK.
Do đó ∆CIK cân tại C (*).
Ta có (vì ∆ACI = ∆DCK).
Do đó
Ta suy ra .
Mà (∆ACD đều).
Do đó (**).
Từ (*), (**), ta suy ra ∆CIK là tam giác đều.
Bài 3. Chọn phát biểu sai trong các phát biểu sau.
A. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có ba cạnh bằng nhau;
B. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó hai góc bằng nhau;
C. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có một góc bằng 60°;
D. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó có hai góc bằng nhau.
Bài 4. Cho hình bên.
Chọn đáp án đúng.
A. ∆OPM và ∆ONQ là các tam giác đều;
B. ∆OMN là tam giác đều;
C. ∆OPM và ∆ONQ là các tam giác cân;
D. Cả hai đáp án B, C đều đúng.
Bài 5. Cho . Lấy điểm A thuộc tia phân giác của . Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Bài 6. Cho ∆ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc canh AB sa cho AD = AE. Gọi I là giao điểm của BD và CE. Hỏi ∆IBC là tam giác gì?
A. ∆IBC là tam giác cân tại I;
B. ∆IBC là tam giác cân tại B;
C. ∆IBC là tam giác cân tại C;
D. ∆IBC là tam giác đều.
Bài 7. Cho hình vẽ.
Tam giác đều trong hình vẽ bên là:
A. ∆MNP;
B. ∆PNH;
C. ∆MPH;
D. ∆MNH.
Bài 8: Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm khác phía đối với BC). Tính số đo góc BDA.
Giải:
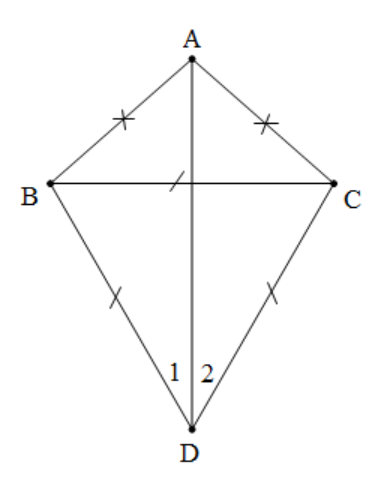
|
GT |
(D và A nằm khác phía đối với BC) |
|
KL |
|
Xét và có:
AB = AC ( cân)
BD = CD ( đều)
Cạnh AD chung
Do đó:
(hai góc tương ứng)
Mặt khác, đều nên
Vậy .
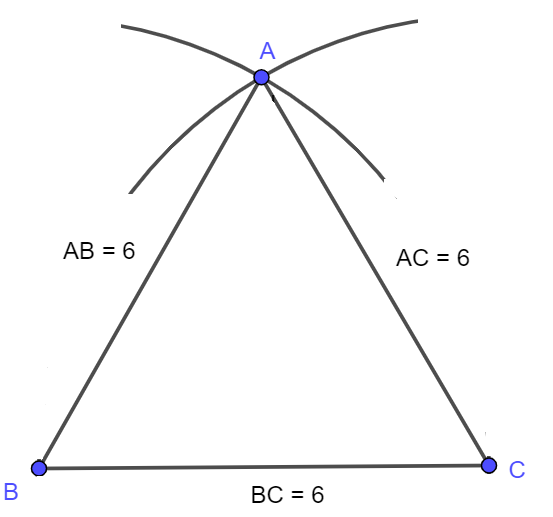
Bài 9: Vẽ tam giác đều ABC có AB = AC = BC = 6cm
Lời giải:
Cách vẽ:
- Vẽ đoạn thẳng BC = 6 cm.
- Vẽ cung tròn tâm C bán kính 6 cm.
- Vẽ cung tròn tâm B bán kính 6 cm.
- Hai cung tròn này cắt nhau tại A.
- Nối AB, AC ta được tam giác ABC cần vẽ.
Bài 10: Cho điểm M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC và BMD. Gọi E, F theo thứ tự là trung điểm của AD, CB. Chứng minh: MEF là tam giác đều.
Lời giải:
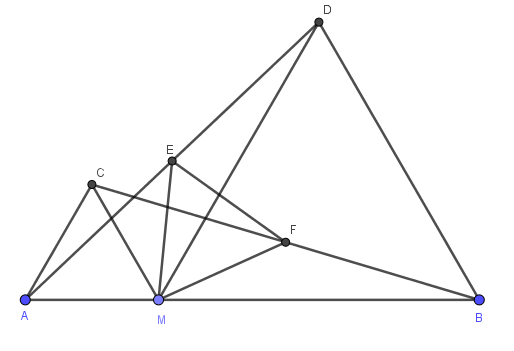
AMD =DCMB (c.g.c)
, AD = CB, AE = CF
Có: MAE =MCF (c.g.c)
ME = MF,
Mà cân (do ME = MF)
đều.
Bài 11. Chọn phát biểu sai:
A. Tam giác đều có ba cạnh
B. Ba cạnh của tam giác đều bằng nhau
C. Bốn góc của tam giác đều bằng nhau
D. Tam giác đều có ba đỉnh
Trả lời:
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Đáp án: C
Bài 12: Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
A. 8
B. 2
C. 4
D. 6
Trả lời:
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Đáp án: D
Bài 13: Cho tam giác đều MNP có MN = 5cm, khẳng định nào sau đây đúng?
A. NP = 3cm
B. MP = 4cm
C. NP = 6cm
D. MP = 5cm
Trả lời:
Trong tam giác đều ba cạnh bằng nhau mà MN = 5cm nên ta có: MN = NP = MP = 5cm
=> Chọn D
Bài 14: Cho tam giác ABC đều với cạnh bằng 6cm. Gọi M, N , P lần lượt là trung điểm của cạnh AB, AC, BC.
a. Chứng minh các tam giác AMN, BMP, CNP, MNP đều.
b. Tính diện tích các tam giác ABC, AMN, BMP, CNP, MNP
Hướng dẫn:
a. Vì tam giác ABC đều nên
Vì M, N, P lần lượt là trung điểm của AB, AC, BC nên:
AM = MB = AN = NC = BP = PC
Xét tam giác AMN có:
AM = AN
Suy ra, tam giác AMN đều.
Tương tự, ta chứng minh được các tam giác BMP, CNP đều.
Vì ba tam giác AMN, BMP, CNP đều nên MN = MP = PN
Suy ra, tam giác MNP đều.
b. Vì tam giác ABC đều nên
Theo giả thiết ta có BC = 6cm, BM = 3cm
Áp dụng định lí Pytago vào tam giác vuông CMB ta có:
Khi đó, diện tích tam giác ABC là:
Bài 15: Cho tam giác ABC có 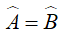
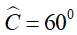
Hướng dẫn:
Xét tam giác ABC có:
Vậy tam giác ABC đều.