Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 104)

Minh Nguyệt Ngày: 19-11-2024 Tổng hợp kiến thức

218

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 104)

Câu 1: Chứng minh rằng với mọi số tự nhiên n khác 0 thì các phân số sau là phân số tối giản $\frac{n}{n + 1}$

Phương pháp giải:

Giả sử $d$ là ước chung lớn nhất (UCLN) của $n$ và $n+1$ .

Sử dụng tính chất của UCLN để chứng minh rằng $d = 1$ , tức là $n$ và $n+1$ không có ước chung nào khác ngoài 1.

Lời giải:

Gọi d là UCLN(n; n+1)

Suy ra: n chia hết cho d; n+1 chia hết cho d (1)

=> (n+1) - n chia hết cho d

=> 1 chia hết cho d (2)

Từ (1) và (2) => d = $\pm$ 1

Vậy $\frac{n}{n + 1}$ là phân số tối giản

Câu 2: Tìm x, y biết: $\frac{x}{3} = \frac{y}{7} v à x y = 84$

Phương pháp giải:

Từ phương trình $\frac{x}{3} = \frac{y}{7}$ , suy ra mối quan hệ giữa $x$ và $y$ .

Biến đổi phương trình để tìm biểu thức của $y$ theo $x$ (hoặc ngược lại).

Thay biểu thức đó vào phương trình $xy = 84$ để tìm giá trị của $x$ và $y$ .

Lời giải:

$\frac{x}{3} = \frac{y}{7}$

Theo tính chất của dãy tỉ số bằng nhau ta có :

$\frac{x}{3} = \frac{y}{7} = \frac{x y}{3.7} = \frac{84}{21} = 4$

$\frac{x}{3} = 4 \Rightarrow x = 3.4 = 12$

$\frac{y}{7} = 4 \Rightarrow y = 4.7 = 28$

Vậy x = 12 , y = 28

Câu 3: Hai số tự nhiên có tổng là 140. Đem số lớn chia cho số bé thì được thương là 5 dư 2

Phương pháp giải:

Biểu diễn hai số tự nhiên dưới dạng sơ đồ đoạn thẳng.

Gọi số bé là một đoạn thẳng ngắn.

Số lớn được biểu diễn bằng 5 lần số bé cộng thêm một đoạn dư 2 đơn vị.

Tổng của hai số là 140. Theo sơ đồ:

Ta có tổng của số bé và số lớn bằng $5$ đoạn của số bé cộng thêm 1 đoạn nữa của số bé và 2 đơn vị.

Thiết lập phương trình từ sơ đồ và tìm 2 số đó.

Lời giải:

Vì đem số lớn chia cho số bé thì được thương là 5 dư 2 suy ra số lớn gấp 5 lần số bé và 2 đơn vị. Ta có sơ đồ:

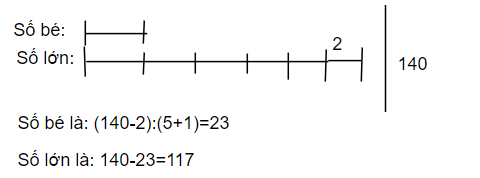
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 104) (ảnh 1)

Câu 4: 20 pound hay 40 kilogram nặng hơn

A. Bằng nhau

B. 20 pound

C. 40 kilogram

Phương pháp giải:

1 pound = 0,45359237 kg

1 kilogam = 2.20462262 pound

Lời giải:

20 pound $\approx 9$ kg

40 kg > 9 kg

Nên đáp án đúng là C.

Câu 5: Rút gọn biểu thức $A = \frac{s i n 3 x + c o s 2 x - s i n x}{c o s x + s i n 2 x - c o s 3 x}$

( sin2x ≠0; 2sinx +1 ≠0)

Phương pháp giải:

Sử dụng các công thức lượng giác để biến đổi biểu thức, bao gồm:

$\sin(3x)$ và $\cos(3x)$ (có thể mở rộng bằng các công thức cộng và nhân đôi).

$\sin(2x)$ và $\cos(2x)$ sử dụng công thức nhân đôi.

Đơn giản hóa từng phần tử trong tử số và mẫu số của biểu thức nếu có thể, và sử dụng các phép biến đổi lượng giác để đưa biểu thức về dạng đơn giản nhất.

Kiểm tra điều kiện xác định của biểu thức để đảm bảo không vi phạm điều kiện đề bài: $\sin(2x) \neq 0$ và $2\sin(x) + 1 \neq 0$ .

Kết quả cuối cùng là dạng rút gọn của $A$ .

Lời giải:

$A = \frac{s i n 3 x - s i n x + c o s 2 x}{c o s x - c o s 3 x + s i n 2 x} = \frac{2 c o s 2 x . s i n x + c o s 2 x}{2 s i n 2 x . s i n x + s i n 2 x} = \frac{c o s 2 x (2 s i n x + 1)}{s i n 2 x (2 s i n x + 1)} = \frac{c o s 2 x}{s i n 2 x} = c o t 2 x$

Câu 6: Tìm n thuộc số tự nhiên sao cho:

a, n + 2 chia hết cho n - 1

b, 2n + 1 chia hết cho 6 - n

Phương pháp giải:

a. Tìm $n$ sao cho $n + 2$ chia hết cho $n - 1$ :

Viết lại $n + 2 = (n - 1) + 3$ .

Điều kiện để $n + 2$ chia hết cho $n - 1$ là 3 phải chia hết cho $n - 1$ .

Tìm các giá trị của $n - 1$ thuộc tập các ước của 3, từ đó suy ra giá trị của $n$ .

b. Tìm $n$ sao cho $2n + 1$ chia hết cho $6 - n$ :

Viết lại $2n + 1 = k(6 - n)$ với $k$ là một số nguyên.

Giải phương trình này để tìm các giá trị của $n$ thỏa mãn.

Lời giải:

a, n + 2 = (n - 1) + 3

ta có vì (n - 1) chia hết cho (n - 1)

Suy ra 3 chia hết cho (n - 1)

Vậy (n - 1) thuộc ước của 3

Ư(3) = {1; -1; 3; -3}

TH1 n - 1 = 1 suy ra n = 2 (tm)

TH2 n - 1= -1 suy ra n = 0 (tm)

TH3 n - 1 = 3 suy ra n = 4 (tm)

TH4 n - 1= -3 suy ra n = -2 (ko tm)

Vậy n = {2; 0; 4}.

2n + 1 chia hết cho 6 - n

có 6 - n chia hết cho 6 - n => 2(6 - n) chia hết cho 6 - n

2n + 1 + 2(6 - n) chia hết cho 6 - n

2n + 1 + 12 - 2n chia hết cho 6 - n

13 chia hết cho 6 - n

=> 6 - n thuộc Ư(13) = {1; -1; 13; -13}

=> n thuộc {5; 7; 19}

Vậy 2n + 1 chia hết cho 6 - n khi n thuộc {5; 7; 19}.

Câu 7: Tìm x biết:

a) $2 x - 2^{2} = 3^{2}$

b) $3^{2} - 3 x = 3$

c) $3^{2} . (- 5) - 5 . 2^{3}$

Phương pháp giải:

Tính toán số mũ sau đó tìm x và kết luận.

Lời giải:

a) 2x - 2² = 3²
=> 2x - 4 = 9
=> 2x = 9 + 4
=> 2x = 13

=> x = $\frac{13}{2}$

b) 3² - 3x = 3

=> 3.3 - 3x = 3

=> 3.(3 - x)=3

=> 3 - x = 1

=> x = 3 - 1 = 2

c) 3² . (-5) - 5.2³

= 9.(-5) - 5.8

= -45 - 40 = -85

Câu 8: 1) Một con ngựa kéo một cái xe bằng lực kéo 250N. Xe chạy với vận tốc 8,5km/h. Coi ma sát là không đáng kể, hãy tính công suất của con ngựa bằng đơn vị mã lực. Cho biết một mã lực (CV) bằng 736W.

2) Người ta dùng một máy có công suất P = 8 kW và hiệu suất H = 85 % để nâng hàng từ mặt đất lên độ cao 5m. Máy đã làm việc trong 10 giờ. Hỏi máy đã nâng được bao nhiêu tấn hàng?

Phương pháp giải:

1) Áp dụng công thức tính công suất.

2) Tính công phục vụ việc nâng hàng.

Trọng lượng hàng được nâng từ đó tính khối lượng theo công thức đã học.

Lời giải:

1) 8,5km/h = $\frac{85}{36}$ m/s

Công suất của ngựa:

$P = F . v = 250. \frac{85}{36} = 590, 3 W$

Công suất của ngựa ra CT mã lực: $\frac{590, 3}{736} = 0, 8 H P$ .

Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 104) (ảnh 1)

Câu 9: Một hình chữ nhật có chu vi 28cm, chiều dài hơn chiều rộng 2 cm. Tìm diện tích hình chữ nhật?

Phương pháp giải:

Từ chu vi tính được tổng chiều dài và chiều rộng.

Tính chiều dài, chiều rộng khi biết tổng hiệu.

Tìm diện tích và kết luận.

Lời giải:

Tổng của chiều dài và chiều rộng là:

28 : 2 = 14 cm

Chiều dài hình chữ nhật là:

(14 + 2) : 2 = 8 cm

Chiều rộng hình chữ nhật là:

8 - 2 = 6 cm

Diện tích hình chữ nhật là:

8x6 = 48 cm²

Đáp số: 48 cm²

Câu 10: Trung bình một người đàn ông có bao nhiêu ngày sinh nhật?

Phương pháp giải:

Mỗi người chỉ có một ngày sinh duy nhất trong năm mà họ chào đời, nên mỗi người chỉ có một "ngày sinh nhật" trong đời.

Lời giải:

Trung bình, mỗi người đàn ông (và thực ra là mọi người) chỉ có 1 ngày sinh nhật – là ngày họ chào đời.

Còn nếu tính các ngày kỷ niệm sinh nhật mỗi năm thì đó là ngày lặp lại, không phải là "ngày sinh" đầu tiên.

Câu 11: Phân tích đa thức thành nhân tử: 0,125.(a + 1)³- 1

Phương pháp giải:

Áp dụng công thức $a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$

Lời giải:

$0, 125. {(a + 1)}^{3} - 1 = {(0, 5 a + 0, 5)}^{3} - 1 = (0, 5 a + 0, 5 - 1) [{(0, 5 a + 0, 5)}^{2} + (0, 5 a + 0, 5) + 1] = 0, 5 (a - 1) (0, 25 a^{2} + 0, 5 a + 0, 25 + 0, 5 a + 0, 5 + 1) = (0, 5 a - 0, 5) (0, 25 a^{2} + a + 1, 75)$

Câu 12: Tính tổng S = 2 + 4 + 6 + ... + 100

Phương pháp giải:

Bước 1: Xác định số hạng cuối cùng và số hạng đầu tiên.

Bước 2: Tính số lượng số hạng trong dãy số.

Số các số hạng = (số cuối - số đầu) : khoảng cách + 1

Bước 3: Tính tổng dãy số.

Tổng dãy số = (số đầu + số cuối) x số các số hạng : 2

Lời giải:

Ta có: dãy số trên là dãy số chẵn liên tiếp,nên sẽ cách nhau 2 đơn vị

Vậy số số hạng của dãy số trên là:

(100 - 2) : 2 + 1 = 50 (số hạng)

Tổng của dãy số là:

(2 + 100) x 50 : 2 = 2550

Câu 13: Cho: x + 2y = 1. Tìm GTLN của A = xy

Phương pháp giải:

Bất đẳng thức có được từ hằng đẳng thức dạng ${(a - b)}^{2} \geq 0$

$a^{2} + b^{2} \geq 2 a b; a b \leq {(\frac{a + b}{2})}^{2}; a^{2} + b^{2} \geq \frac{1}{2} {(a + b)}^{2} .$ Dấu bằng xảy ra khi và chỉ khi $a = b .$

Lời giải:

. Khi đó:

$A = (1 - 2 y) y = y - 2 y^{2} = - (2 y^{2} - y) = - [2 (y^{2} - \frac{y}{2} + \frac{1}{4^{2}}) - \frac{1}{8}]$

$= \frac{1}{8} - 2 (y - \frac{1}{4})^{2} \leq \frac{1}{8}$

Vậy $A_{m a x} = \frac{1}{8}$

Giá trị này đạt tại $y - \frac{1}{4} = 0 \Leftrightarrow y = \frac{1}{4}$

$x = 1 - 2. \frac{1}{4} = \frac{1}{2}$

Câu 14: Trong một trò chơi, học sinh lớp 3A xếp thành một vòng tròn. Các bạn xếp xen kẽ: bắt đầu là 1 bạn nam, 1 bạn nữ rồi lại đến 1 bạn nam, 1 bạn nữ, cuối cùng là 1 bạn nữ. Tất cả có 20 bạn nam. Hỏi lớp 3A có bao nhiêu bạn?

Phương pháp giải:

Phân tích đề bài: xếp xen kẽ: bắt đầu là 1 bạn nam, 1 bạn nữ rồi lại đến 1 bạn nam, 1 bạn nữ, cuối cùng là 1 bạn nữ ta được số nam bằng nữ.

Tính số nữ và tính tổng số học sinh trong lớp.

Lời giải:

Các bạn xếp xen kẽ: bắt đầu là 1 bạn nam, 1 bạn nữ, rồi lại đến 1 bạn nam, 1 bạn nữ, cuối cùng là một bạn nữ, tức là số bạn nữ bằng số bạn nam.

Mà số bạn nam là 20 bạn nên số bạn nữ cũng là 20 bạn

Vậy số bạn lớp 3A là:

20 + 20 = 40 (bạn)

Đáp số: 40 bạn

Câu 15: Từ 1 đến 99 có bao nhiêu số lẻ?

Phương pháp giải:

Nếu dãy số có quy luật cách đều nghĩa là mỗi số hạng đứng sau bằng số hạng liền trước cộng với số không đổi d thì:

Số các số hạng của dãy = (Số hạng lớn nhất – Số hạng nhỏ nhất) : d + 1

Lời giải:

Có tất cả: (99 - 1) : 2 + 1 = 50 (số lẻ, số chẵn)

Vì khoảng cách các số hạng đều bằng 2

Câu 16: Tính 1.2 + 2.3 + 3.4 +…+ 99.100

Phương pháp giải:

Đặt A là tổng cần tính.

Nhóm các số hạng chung để giải quyết bài toán.

Lời giải:

Đặt A = 1.2+2.3 +.......+99.100

3A= 1.2.3+2.3.4+3.4.3 +......+ 99.100.3

3A= 1.2. (3 - 0) + 2.3.(4 - 1) +3.4. (5 - 2)....... . 99.100. (101 - 98)

3A = (1.2.3 + 2.3.4 + 3.4.5 +...... + 99.100.101) - (0.1.2 + 1.2.3 + 2.3.4 +.......+ 98.99.100)

3A = 99.100.101 - 0.1.2

3A = 999900 - 0

3A= 999900

A= 999900 : 3

A = 333300

Câu 17: Một người đi từ A đến B. Người đó đi 1/3 quãng đường với vận tốc 20 km/h rồi đi phần còn lại với vận tốc 10 km/h. Hỏi vận tốc trung bình trên quãng đường AB của người đó là bao nhiêu?

Phương pháp giải:

Đặt quãng đường là x.

Tính thời gian người đó đi quãng đường đầu và quãng đường còn lại.

Tính vận tốc trung bình trên AB và kết luận.

Lời giải:

Gọi độ dài quãng đường AB là $x (k m)$ , $x > 0$ .

Thời gian người đó đi $\frac{1}{3}$ quãng đường đầu là: $\frac{\frac{1}{3} x}{20} = \frac{x}{60}$ (giờ)

Thời gian người đó đi quãng đường còn lại là: $\frac{\frac{2}{3} x}{10} = \frac{x}{15}$ (giờ)

Vận tốc trung bình trên quãng đường AB của người đó là: $\frac{x}{\frac{x}{60} + \frac{x}{15}} = \frac{1}{\frac{1}{60} + \frac{1}{15}} = 12 (k m / h)$ .

Câu 18: Chứng minh rằng $81^{7} - 27^{9} - 9^{13}$ chia hết cho 45

Phương pháp giải:

Biểu diễn các số dưới dạng lũy thừa cơ số 3.

Đặt nhân tử chung và kết luận.

Lời giải:
$8 1^{7} - 2 7^{9} - 9^{13} = {(3^{4})}^{7} - {(3^{3})}^{9} - {(3^{2})}^{13} = 3^{28} - 3^{27} - 3^{26} = 3^{24} . (3^{4} - 3^{3} - 3^{2}) = 3^{24} . (81 - 27 - 9) = 3^{24} . 45$

Vì $3^{24} . 45$ nên $8 1^{7} - 2 7^{9} - 9^{13} ⋮ 45$ (đpcm)

Vậy...

Câu 19: Trộn 2 lít dung dịch HCL 4M vào 1 lít dung dịch HCl 0,5M. Tính nồng độ mol của dung dịch mới.

Phương pháp giải:

Nồng độ mol (kí hiệu $C_{M}$ ) của dung dịch cho biết số mol chất tan có trong 1 lít dung dịch.

Công thức: $C_{M} = \frac{n}{V}$ (M hay mol/l)

Trong đó: n: số mol chất tan (mol); V: thể tích dung dịch (lít).

Lời giải:

Số mol HCl trong dung dịch 1 là: $n_{H C l} = C_{M} \times V = 4.2 = 8 (m o l)$

Số mol HCl trong dung dịch 2 là: $n_{H C l} = C_{M} \times V = 1.0, 5 = 0, 5 (m o l)$

Thể tích dung dịch mới là: $V_{d d m ớ i} = V_{d d 1} + v_{d d 2}$ =2+1=3(l)

Nồng độ mol của dung dịch mới là: $C_{M} = \frac{n}{V} = \frac{0, 5 + 8}{3} \approx 2, 833 %$

Câu 20: Tìm:

a. 15% của 400

b. 12,5% của 130kg

c. 24%của 125m²

d. 0,2%của 720m

e. 6% của 172dm²

g. 5% của 1200 cây

Phương pháp giải:

Để tìm một phần trăm của một số, ta thực hiện các bước sau:

Lấy số đó nhân với phần trăm cần tìm.

Chia kết quả cho 100.

Lời giải:

a, 15% của 400 là: 400 x 15: 100 = 60

b, 12,5% của 130 kg là: 130 12,5 : 100 = 16,25 (kg)

c, 24% của 125 m2 là: 125 24: 100 = 30 (m²)

d, 0,2% của 720 m là: 1,44 (m)

e, Tìm 6% của 172 dm2 là: 172 x 6: 100 = 10,32 (dm²)

g, 5% của 1 200 cây là: 1200 5: 100 = 60 (cây)

Câu 21: Tính A = $7 x - 2 x - \frac{2}{3} y + \frac{7}{9} y$ với x = $\frac{- 1}{10}$ ; y = 4,8

Phương pháp giải:

Nhóm x vào một nhóm, y vào 1 nhóm.

Thay x, y đã cho vào và tính giá trị A.

Lời giải:

$A = 7 x - 2 x - \frac{2}{3} y + \frac{7}{9} y - 3 x$

$A = (7 x - 2 x - 3 x) + (\frac{7}{9} y - \frac{2}{3} y)$

$A = 2 x + \frac{1}{9} y$

Thay $x = - \frac{1}{10}; y = 4, 8$ vào $A$

$A = 2 . (- \frac{1}{10}) + \frac{1}{9} .4, 8$

$A = - \frac{1}{5} + \frac{8}{15}$

$A = \frac{1}{3}$

Vậy $A = \frac{1}{3}$ với $x = - \frac{1}{10}; y = 4, 8$

Câu 22: So sánh 4²⁰⁰ và 2⁴⁰⁰

Phương pháp giải:

Phân tích 4²⁰⁰ về dạng 2^x và so sánh.

Lời giải:

$= {(2^{2})}^{200}$

$= 2^{2.200} = 2^{400}$

Vậy $4^{200} = 2^{400}$

Câu 23: Tìm x biết: $125 x^{3} - {(2 x + 1)}^{3} - {(3 x - 1)}^{3} = 0$

Phương pháp giải:

Áp dụng công thức:

Lập phương của một hiệu, tổng

Công thức: (A – B)³ = A³ – 3A²B + 3AB² – B³

(A – B)³ = A³ + 3A²B + 3AB² + B³

Lời giải:

$125 x^{3} - {(2 x + 1)}^{3} - {(3 x - 1)}^{3} = 0$

$\Leftrightarrow 125 x^{3} - (8 x^{3} + 12 x^{2} + 6 x + 1) - (27 x^{3} - 27 x^{2} + 9 x - 1) = 0$

$\Leftrightarrow 125 x^{3} - 8 x^{3} - 12 x^{2} - 6 x - 1 - 27 x^{3} + 27 x^{2} - 9 x + 1 = 0$

$\Leftrightarrow 90 x^{3} + 15 x^{2} - 15 x = 0$

$\Leftrightarrow 15 x . (6 x^{2} + x - 1) = 0$

$\Leftrightarrow 15 x . (6 x^{2} + 3 x - 2 x - 1) = 0$

$\Leftrightarrow 15 x . [3 x . (2 x + 1) - (2 x + 1)] = 0$

$\Leftrightarrow 15 x . (2 x + 1) . (3 x - 1) = 0$

$\Leftrightarrow$ $[\begin{array}{l} x = 0 \\ x = \frac{- 1}{2} \\ x = \frac{1}{3} \end{array}$

Vậy $S \in {0; \frac{- 1}{2}; \frac{1}{3}}$

Câu 24: Rút gọn phân số $\frac{202020}{454545}$ thành phân số tối giản.

Phương pháp giải:

Tìm Ước chung lớn nhất (ƯCLN) của tử số và mẫu số.

Chia cả tử số và mẫu số cho ƯCLN để thu được phân số tối giản.

Lời giải:

Tìm ƯCLN của $202020$ và $454545$ .

Ta thấy $202020$ và $454545$ đều chia hết cho $10101$ .

$\frac{202020}{10101} = 20$

$\frac{454545}{10101} = 45$

Vậy ta đã rút gọn phân số thành $\frac{20}{45}$ .

ƯCLN của $20$ và $45$ là $5$ .

Chia cả tử số và mẫu số cho $5$ :

$\frac{20}{5} = 4$

$\frac{45}{5} = 9$

Vậy phân số tối giản là $\frac{4}{9}$ .

Câu 25: Một ô tô chạy từ A đến B với vận tốc là 65km/h , cùng lúc đó thì 1 xe máy chạy từ B về A với vận tốc 40km/h. Biết khoảng cách AB là 540 km và M là trung điểm của AB. Hỏi sau khi khởi hành bao lâu thì ô tô cách M 1 khoảng cách bằng 1/2 khoảng cách xe máy đến điểm M.

Phương pháp giải:

Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.

Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc. Do đó lập được phương trình và tìm t.

Lời giải:

Quãng đường AB dài 540km nên nửa quãng đường AB dài 270km.

Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.

Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc. Do đó:

$\frac{S_{1}}{V_{1}} = \frac{S_{2}}{V_{2}} = t$ (t là thời gian cần tìm)

Ta có: $t = \frac{270 - a}{65} = \frac{270 - 2 a}{40}$

$\Rightarrow t = \frac{540 - 2 a}{130} = \frac{270 - 2 a}{40} = \frac{(540 - 2 a) - (270 - 2 a)}{130 - 40} = \frac{270}{90} = 3$

Vậy sau khi khởi hành 3 giờ thi ô tô cách M 1 khoảng cách bằng 1/2 khoảng cách xe máy đến M.

Câu 26: Tính nhanh: M = $\frac{1}{4} + \frac{1}{28} + \frac{1}{70} + \frac{1}{130} + . . . . .$ ( M có 30 số hạng )

Phương pháp giải:

Tìm quy luật của dãy số trên. Từ đó tính giá trị M.

Lời giải:

Ta có:

$M = \frac{1}{1.4} + \frac{1}{4.7} + \frac{1}{7.10} + \frac{1}{10.13} + . . .$

Dựa vào quy luật trên => Số hạng thứ 30 là: $\frac{1}{98.101}$

$\Rightarrow 3 M = 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{10} + . . . + \frac{1}{98} - \frac{1}{101}$

$\Rightarrow M = (1 - \frac{1}{101}) : 3 = \frac{100}{101} . \frac{1}{3} = \frac{100}{303}$

Câu 27: Cho a + b + c = 1 và $\frac{1}{a} + \frac{1}{b} + \frac{1}{c}$ = 0. Tính $a^{2} + b^{2} + c^{2}$

Phương pháp giải:

Biểu diễn điều kiện thứ hai.

Sử dụng hằng đẳng thức.

Thay vào giá trị $a + b + c = 1$ và $ab + b c + c a = 0$

Lời giải:

$a, \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0 = > \frac{a b + b c + a c}{a b c} = 0 = > a b + b c + a c = 0. a b c = 0$

Mà $a + b + c = 1 = > {(a + b + c)}^{2} = 1 = > a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 a c = 1$

$= > a^{2} + b^{2} + c^{2} + 2 (a b + b c + a c) = 1 = > a^{2} + b^{2} + c^{2} = 1 - 0 = 1$ (vì ab+bc+ac=0)

ìm n thuộc N để:

a) Đơn thức A $= 5 x^{n} . y^{3}$ chia hết cho đơn thức B = $4 x^{3} y$

b) Đa thức M = $9 x^{8} y^{n} - 15 x^{n} y^{5}$ chia hết cho đơn thức N = $6 x^{3} y^{2}$

Phương pháp giải:

Để tìm $n$ thuộc $\mathbb{N}$ sao cho các đơn thức hoặc đa thức chia hết cho nhau, ta cần xét điều kiện chia hết của các biến và các hệ số.

Điều kiện chia hết của đơn thức: Để đơn thức $A$ chia hết cho đơn thức $B$ , bậc của mỗi biến trong $A$ phải lớn hơn hoặc bằng bậc của biến tương ứng trong $B$ , và hệ số của $A$ phải chia hết cho hệ số của $B$ .

Điều kiện chia hết của đa thức: Để đa thức $M$ chia hết cho đơn thức $N$ , mỗi đơn thức trong $M$ phải chia hết cho $N$ .

Lời giải:

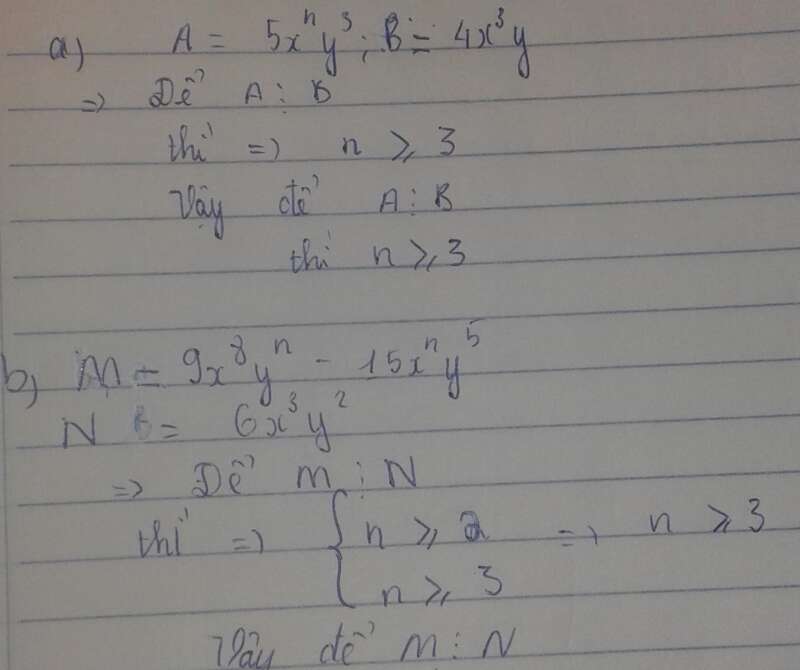
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 104) (ảnh 2)

Câu 29: Tìm x: $\frac{11}{15} - (\frac{7}{9} + x) . \frac{3}{8} = \frac{61}{90} + \frac{x}{3}$

Phương pháp giải:

Nhóm các phần tử không chứa x vào một nhóm thực hiện tính toán.

Tính toán các phần tử có x và thực hiện tìm x.

Lời giải:

$\frac{11}{15} - (\frac{7}{9} + x) . \frac{3}{8} = \frac{61}{90} + \frac{x}{3}$ (. là dấu nhân)

$\Leftrightarrow \frac{11}{15} - \frac{7}{24} - \frac{3 x}{8} - \frac{61}{90} - \frac{x}{3} = 0$

$\Leftrightarrow \frac{- 17}{72} - (\frac{3 x}{8} + \frac{x}{3}) = 0$

$\Leftrightarrow \frac{17 x}{24} = - \frac{17}{72}$

$\Leftrightarrow 17 x . 72 = - 17.24$

$\Leftrightarrow x = - \frac{1}{3}$

Câu 30: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).

Phương pháp giải:

Áp dụng định lý Talet đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Lời giải:

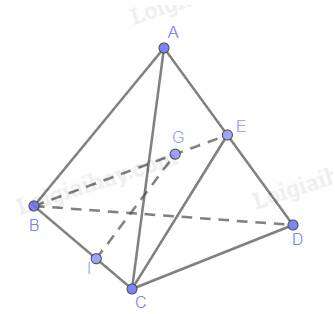
Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 104) (ảnh 1)