Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Mô đun số phức: Phương pháp giải và bài tập vận dụng, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mô đun số phức: Phương pháp giải và bài tập vận dụng

1. Định nghĩa về mô đun số phức

Modun (Tiếng Anh: modulus hoặc absolute) của số phức z = a+bi (a, b∈R) là căn bậc hai số học (hay căn bậc hai không âm) của a² + b². Chẳng hạn như z = 3 + 4i có 3² + 4²=25 nên modun của 3 + 4i bằng 5. Ta cũng ký hiệu modun của z = a+bi là |z| hoặc |a + bi|. Với lưu ý số thực cũng là một số phức. Ta cũng dễ nhận thấy rằng trị tuyệt đối của một số thực cũng chính là modun của số thực đó. Do đó đôi khi ta cũng gọi mô đun của số phức là giá trị tuyệt đối cúa số phức.

Ví dụ:

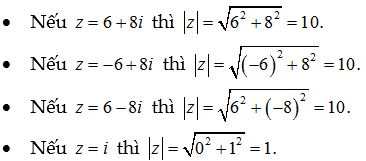
Về mặt hình học, mỗi số phức z = a + bi (a,b∈R) được biểu diễn bởi một điểm M(z)=(a;b) trên mặt phẳng Oxy và ngược lại. Khi đó modun của z được biểu diễn bởi độ dài đoạn thẳng OM(z). Rõ ràng, modun của z là một số thực không âm và nó chỉ bằng 0 khi z = 0.

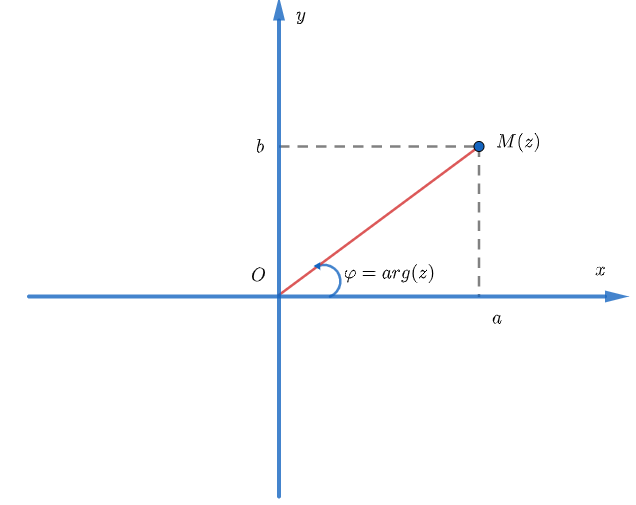
2. Tính chất modun của số phức

Với mô đun của số phức, ta dễ dàng chứng minh được các tính chất sau:

(i) Hai số phức đối nhau có mô đun bằng nhau. Tức là |z|=|-z|.

(ii) Hai số phức liên hợp có mô đun bằng nhau. Tức là |a+bi|=|a-bi|.

(iii) Mô đun của z bằng 0 khi và chỉ khi z=0.

(iv) Tích của hai số phức liên hợp bằng bình phương mô đun của chúng

(v) Mô đun của một tích bằng tích các mô đun

(vi) Mô đun của một thương bằng thương các mô đun

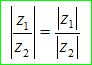
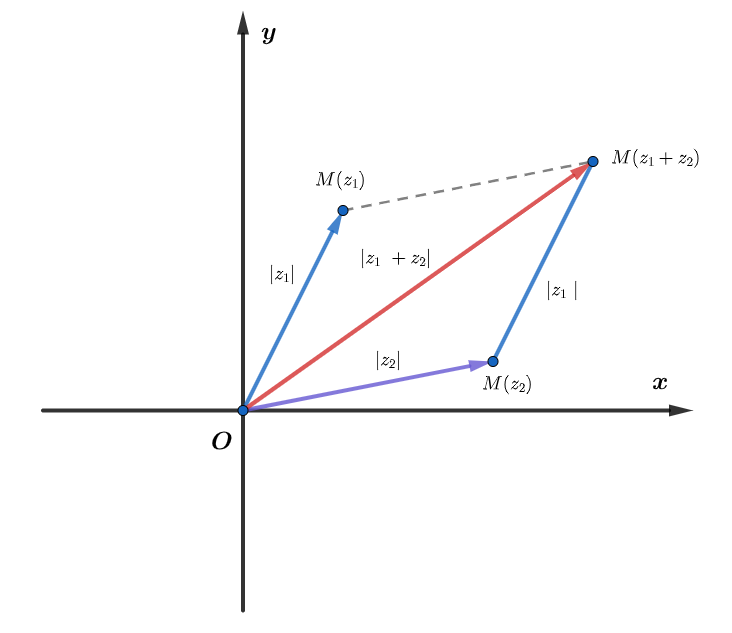
3. Bất đẳng thức mô đun

Vì mô đun của số phức là độ dài đoạn thẳng trong mặt phẳng. Do đó, từ các bất đẳng thức tam giác ta có suy ra được các bất đẳng thức mô đun tương tự.

• Tổng hai cạnh trong một tam giác luôn lớn hơn cạnh thứ ba. Từ đó ta có bất đẳng thức:

Dấu bằng xảy ra khi

Cũng từ bất đẳng thức tam giác nêu trên ta có thể suy ra được:

Dấu bằng xảy ra khi

• Hoàn toàn tương tự từ bất đẳng thức tam giác:”Hiệu hai cạnh trong một tam giác luôn nhỏ hơn cạnh thứ ba ta suy ra được các bất đẳng thức sau:

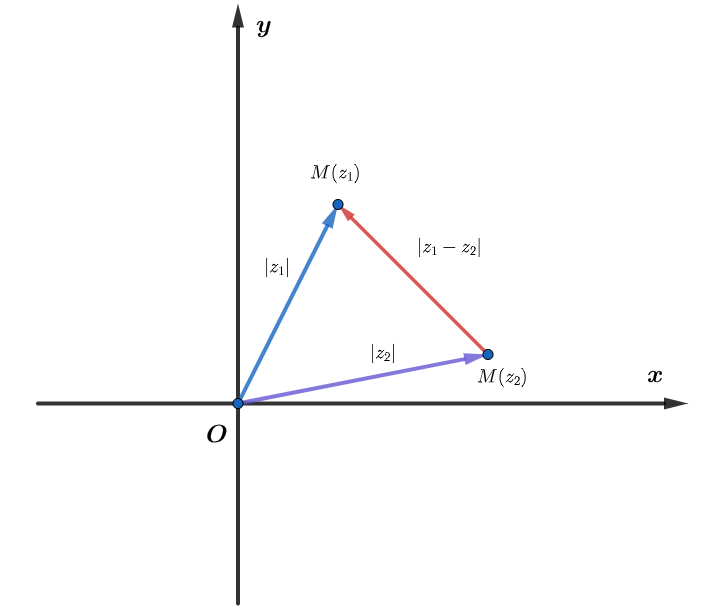
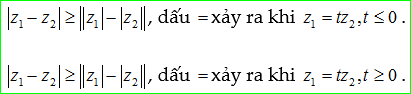
4. Phương pháp giải bài tập

Để giải bài tập được bài tập về mô đun số phức, cần nhớ những kiến thức sau:

 được gọi là môđun của số phức z.

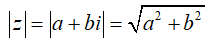
+) Kết quả: ∀z ∈ C ta có:

5. Bài tập vận dụng

Bài 1:Tìm các số phức z thỏa mãn 

A. z₁ = -1 + i; z₂ = 1 - i

B. z₁ = 1 + i; z₂ = -1 - i

C. z₁ = -1 + i ; z₂ = -1 - i

D. z₁ = 1 + i; z₂ = 1 - i

Hướng dẫn:

4(x² + y² ) = 8 → x² + y² = 2

Do đó x = 1 và y = ±1

Chọn D.

Bài 2:: Cho số phức z = 2 - 3i. Tính |z|

A. |z| = 2.         B. |z| = -3.         C. |z| = √13.         D. |z| = 13 .

Hướng dẫn:

Chọn C

Bài 3:Cho hai số phức z₁ = 1 + 3i ; z₂ = 2 - i Tính P = |z₁ + z₂|

A. P = √5 .         B. P = 5         C. P = √10         D. P = √13

Hướng dẫn:

Chọn D.

Bài 4:Cho hai số phức z₁ = 1 - 2i; z₂ = 3 + i . Tính P = |z₁ - 2z₂| .

A. P = √26.         B. P = √41.         C. P = √29.         D. P = √33.

Hướng dẫn:

Ta có: 2z₂ = 6 + 2i

Chọn B.

Bài 5:Cho số phức z = (3-2i)(1+i)². Môđun của w = iz +  là

A.2         B.2√2         C. 1         D. √2

Hướng dẫn:

Chọn đáp án B.

Bài 6: Cho số phức z thỏa mãn điều kiện 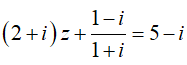 . Môđun của số phức w = 1 + 2z + z² có giá trị là

A. 10.         B. -10.        C. 100.         D. -100.

Hướng dẫn:

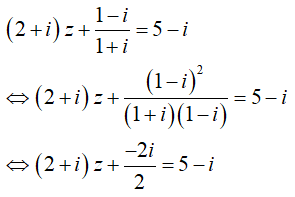
Chọn đáp án A.

Bài 7:Cho số phức z = 5 - 3i. Tính |z| .

A. |z| = 34         B.|z| = 2         C. |z| = √34         D. |z| = 4

Hướng dẫn:

Chọn C.

Bài 8:Cho số phức z = 1 + 2i. Tính |z| .

A. |z| = 1.         B. |z| = √5.         C. |z| = 2.         D. |z| = 3.

Hướng dẫn:

Ta có 

Chọn B.

Bài 9: Cho số phức z = -3 + 2i. Tính |z + 1 - i| .

A. P = 4         B. P = 1         C. P = √5 .         D. P = 2√2 .

Hướng dẫn:

Chọn C.

Bài 10:Cho hai số phức z₁ = 3 - 2i; z₂ = -2 + i Tính P = |z₁ + z₂| .

A. P = √5.         B. P = √2.         C. P = √13         D. P = 2

Hướng dẫn:

Ta có: z₁ + z₂ = (3 - 2i) + (-2 + i) = 1 - i

|z₁ + z₂| = |1 - i| = √2

Chọn B.

Bài 11:Cho hai số phức z₁ = 2 + 6i; z₂ = -1 + 2i. Tính P = |z₁ - z₂| .

A. P = 5         B. P = 6         C. P = 7         D. P = 8

Hướng dẫn:

Ta có: z₁ - z₂ = (2 + 6i) - (-1 + 2i) = 3 + 4i

Chọn A

Bài 12: , Cho hai số phức z₁ = 3 + i; z₂ = 2 - i. Tính P = |z₁ + z₁z₂| .

A. P = 10        B. P = 50        C. P = 5        D. P = 85

Hướng dẫn:

Ta có

z₁z₂ = (3 + i)(2 - i) = 6 - 3i + 2i - i² = 7 - i ,

z₁ + z₁z₂ = 3 + i + 7 - i = 10.

Chọn A.

Câu 13: Cho số phức z thỏa mãn điều kiện |z - 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích:

A. S = 9π    B. S = 12π.    C. S = 16π.    D.S = 25π.

Hướng dẫn:

Ta có:

<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)

Giả sử w = x + yi, khi đó (1) <=> (x - 7)² + (y + 9)² ≤ 16

Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4

Vậy diện tích cần tìm là S = π.4² = 16π

Chọn C.

Câu 14: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức

A.5    B.4    C.6    D.8

Hướng dẫn:

Ta có:

Khi z = i thì A = 6

Chọn C.

Câu 15. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất max M và giá trị nhỏ nhất min M của biểu thức M = |z² + z + 1| + |z³ + 1|

A. max M = 5; min M = 1   B. max M = 5; min M = 2

C. max M = 4; min M = 1   D.max M = 4; min M = 2

Hướng dẫn:

Ta có: M ≤ |z|² + |z| + 1 + |z|³ + 1 = 5 ,

khi z = 1 thì M = 5 nên max M = 5

Mặt khác:

khi z = -1 thì M = 1 nên min M = 1

Chọn A.