Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 97)

Câu 1: 40 : 3 bằng bao nhiêu

Phương pháp giải: Phép chia có dư là phép chia có số dư lớn hơn 0 nhỏ hơn số chia.

Lời giải:

 

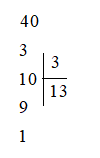
Vậy 40 : 3 bằng 13 dư 1

Câu 2: Viết tiếp 2 số hạng vào dãy số sau

A. 100; 93; 85; 76;…; …

B. 10; 13; 18; 26; ....; …

C. 0; 1; 2; 4; 7; 12; ....; …

D. 0; 1; 4; 9; 16; ....; …

E. 5; 6; 8; 10; …; …

Phương pháp giải: Xác định được quy luật của từng dạy số hạng

Lời giải:

a) Vì 100 – 93 = 7, 93 – 85 = 8, 85 – 76 = 9

=> Dãy số hạng tuân theo quy luật giảm dần từ 7, 8, 9, 10… đơn vị

=> Hai số tiếp theo là: 76 – 10 = 66, 66 – 11 = 55

b) Vì 10 + 13 – 5 = 18, 13 + 18 – 5 = 26

=> Dãy số hạng tuân theo quy luật tổng hai số liền kề trừ cho 5 ra số hạng tiếp theo

=> Hai số tiếp theo là: 18 + 26 – 5 = 39, 39 + 26 – 5 = 60

c) Vì 0 + 1 + 1 = 2, 1 + 2 + 1 = 4, 4 + 2 + 1 = 7

=> Dãy số hạng tuân theo quy luật số hạng tiếp theo bằng tổng của hai số hạng liền kề trước nó cộng thêm 1 đơn vị

=> Hai số tiếp theo: 7 + 12 + 1 = 20, 20 + 12 + 1 = 33

d) Vì 1 – 0 = 1, 4 – 1 = 3, 9 – 4 = 5

=> Dãy số hạng tuân theo quy luật cộng lần lượt các số lẻ liên tiếp 1, 3, 5, 7… ta được số tiếp theo kề nó

=> Hai số tiếp theo: 16 + 9 = 25, 25 + 11 = 36

e) Vì 5 + 6 – 3 = 8, 8 + 6 – 4 = 10

=> Dãy số hạng tuân theo quy luật số liền sau bằng tổng hai số liền trước trừ đi thứ tự của nó trong dãy.

=> Hai số tiếp theo: 10 + 8 – 5 = 13, 13 + 10 – 6 = 17

Câu 3: Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{(m - 1)x - 2y = 1}\\{3x + my = 1}\end{array}} \right.\)

a) Giải hệ phương trình khi m = \(\sqrt 3  + 1\)

b) Chứng minh rằng hệ phương trình có 1 nghiệm duy nhất với mọi m

c) Tìm m để x-y đạt giá trị nhỏ nhất

Phương pháp giải:

a) Bước 1: Từ một phương trình của hệ phương trình đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại để được một phương trình mới (chỉ còn một ẩn).

Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ phương trình đã cho.

b, c) Bước 1: Sử dụng các phương pháp giải hệ phương trình cơ bản đã học như thế, cộng đại số, ta thu được phương trình mới (chỉ còn một ẩn).

Bước 2: Giải và biện luận phương trình mới, từ đó đi đến kết luận về giải và biện luận hệ phương trình đã cho.

Lời giải:

a) Với m = \(\sqrt 3  + 1\) hệ phương trình có dạng:

\[\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{\sqrt 3 x - 2y = 1}\\{3x + (\sqrt 3  + 1)y = 1}\end{array}} \right.\\ =  > \left\{ {\begin{array}{*{20}{c}}{3x - 2\sqrt 3 y = \sqrt 3 }\\{3x + (\sqrt 3  + 1)y = 1}\end{array}} \right.\\ =  > \left\{ \begin{array}{l}\begin{array}{*{20}{c}}{(3\sqrt 3  + 1)y = 1 - \sqrt 3 }\\{\sqrt 3 x - 2y = 1}\end{array}\\ =  > \left\{ {\begin{array}{*{20}{c}}{y = \frac{{ - 5 + 2\sqrt 3 }}{{13}}}\\{3x + 2.\frac{{ - 5 + 2\sqrt 3 }}{{13}} = 1}\end{array}} \right.\end{array} \right.\\ =  > \left\{ {\begin{array}{*{20}{c}}{y = \frac{{ - 5 + 2\sqrt 3 }}{{13}}}\\{x = \frac{{4 + \sqrt 3 }}{{13}}}\end{array}} \right.\end{array}\]

b) \(\left\{ {\begin{array}{*{20}{c}}{(m - 1)x - 2y = 1(1)}\\{3x + my = 1(2)}\end{array}} \right.\)

Từ (1) ta có: \(y = \frac{{(m - 1)x - 1}}{2}\) thay vào (2) ta được:

\(\begin{array}{l}3x + m.\frac{{(m - 1)x - 1}}{2} = 1\\ =  > 6x + m(m - 1)x - 1 = 2\\ =  > ({m^2} - m + 6)x = 3\\ =  > x = \frac{3}{{{m^2} - m + 6}}\end{array}\)

Mà \({m^2} - m + 6\) luôn có nghiệm

=> ∀m thì đều tìm được một giá trị của y từ đó suy ra giá trị của x

=> Hệ phương trình luôn có 1 nghiệm duy nhất với mọi m

c) \(\left\{ {\begin{array}{*{20}{c}}{(m - 1)x - 2y = 1(1)}\\{3x + my = 1(2)}\end{array}} \right.\)

Từ (1) ta có: \(y = \frac{{(m - 1)x - 1}}{2}\) thay vào (2) ta được:

\(\begin{array}{l}3x + m.\frac{{(m - 1)x - 1}}{2} = 1\\ =  > 6x + m(m - 1)x - m = 2\\ =  > ({m^2} - m + 6)x = 2 + m\\ =  > x = \frac{{2 + m}}{{{m^2} - m + 6}}\\ =  > y = \frac{{m - 4}}{{{m^2} - m + 6}}\end{array}\)

\[\begin{array}{l}x - y = \frac{{2 + m}}{{{m^2} - m + 6}} - \frac{{m - 4}}{{{m^2} - m + 6}}\\ = \frac{6}{{{m^2} - m + 6}} = \frac{6}{{{{\left( {m - \frac{1}{2}} \right)}^2} + \frac{{23}}{4}}}\end{array}\]

Vì \[{\left( {m - \frac{1}{2}} \right)^2} + \frac{{23}}{4}\]≥ \[\frac{{23}}{4}\]

=> \[\frac{6}{{{{\left( {m - \frac{1}{2}} \right)}^2} + \frac{{23}}{4}}}\]≤\(\frac{{24}}{{23}}\)

=> x – y ≤\(\frac{{24}}{{23}}\)

Dấu bằng xảy ra ó m = \(\frac{1}{2}\)(TMĐK)

Vậy x-y đạt giá trị nhỏ nhất bằng \(\frac{{24}}{{23}}\) khi m = \(\frac{1}{2}\)

Câu 4: Tìm x, y biết x(x - y) = \(\frac{3}{{10}}\) và y(x - y) = \( - \frac{3}{{50}}\)

Phương pháp giải:

Bước 1: Từ một phương trình của hệ phương trình đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại để được một phương trình mới (chỉ còn một ẩn).

Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ phương trình đã cho.

Lời giải:

\[\left\{ {\begin{array}{*{20}{c}}{x(x - y) = \frac{3}{{10}}(1)}\\{y(x - y) = \frac{{ - 3}}{{50}}(2)}\end{array}} \right.\]

Lấy (1):(2) => $\frac{x}{y}=-5=>x=-5y$

Thay vào (1) =>

 \(\begin{array}{l} - 5y.\left( { - 5y - y} \right) = \frac{3}{{10}}\\ =  > 30{y^2} = \frac{3}{{10}}\\ =  > {y^2} = \frac{1}{{100}}\\ =  > y =  \pm \frac{1}{{10}} =  > x =  \mp \frac{1}{2}\end{array}\)

Vậy tập nghiệm của phương trình: \(\left( {\frac{{ - 1}}{2};\frac{1}{{10}}} \right)\) và \(\left( {\frac{1}{2};\frac{{ - 1}}{{10}}} \right)\)

Câu 5: Tìm số nguyên tố x để |P| + P = 0 biết \(P = \frac{{\sqrt x  - 3}}{{\sqrt x  + 3}}(x \ge 0,x \ne 4,x \ne 9)\)

Phương pháp giải:

* |x| ≥ 0 với mọi x ∈ Q. Dấu “=” xảy ra khi x = 0

* |x| ≥ x và |x| ≥ -x với mọi x ∈ Q

* |x| ≥ |x| với mọi x ∈ Q

     Với a > 0, ta có:

* |x| = a khi x = ±a

* |x| ≤ a khi  -a ≤ x ≤ a

Lời giải:

Để |P| + P = 0 => P ≤ 0 =>

 \[\begin{array}{l}\left. {\begin{array}{*{20}{c}}{\frac{{\sqrt x  - 3}}{{\sqrt x  + 3}} \le 0}\\{m\`a \sqrt x  + 3 > 0}\end{array}} \right\} =  > \sqrt x  - 3 \le 0\\ =  > \sqrt x  \le 3 =  > 0 \le x \le 9\end{array}\]

Kết hợp với ĐKĐB: \(\left\{ {\begin{array}{*{20}{c}}{0 \le x < 9}\\{x \ne 4}\end{array}} \right.\)

Mà x là số nguyên tố => x = {2, 3, 5, 7}

Câu 6: Tìm số tự nhiên x, y biết 7(x - 2004)² = 23 - y²

Phương pháp giải:

Chia trường hợp của y từ đó tìm các giá trị của x thỏa mãn với yêu cầu đề bài

Lời giải:

23 − y² = 7(x − 2004)² ≥ 0 ⇔ y² ≤ 23

Mà $y\in N\iff y\in \{0;1;2;3;4\}$

Với $y=0\iff 7{(x-2004)}^2=23\left(lo\text{ạ}i\right)$

Với $y=1\iff 7{(x-2004)}^2=22\iff {(x-2004)}^2={\displaystyle \frac{22}{7}}\left(lo\text{ạ}i\right)$

Với $y=2\iff 7{(x-2004)}^2=19\iff {(x-2004)}^2={\displaystyle \frac{19}{7}}\left(lo\text{ạ}i\right)$

Với $y=3\iff 7{(x-2004)}^2=14\iff {(x-2004)}^2=2\left(lo\text{ạ}i\right)$

Với $y=4\iff 7{(x-2004)}^2=7\iff [\begin{array}{c}x-2004=1\\ x-2004=-1\end{array}\iff [\begin{array}{c}x=2005\\ x=2003\end{array}$​

Vậy $(x;y)=(2005;4);(2003;4)$

Câu 7: Bạn Lan đánh số trang sách bằng các số tự nhiên từ 1 đến 216. Bạn Lan phải viết tất cả bao nhiêu chữ số? 

Phương pháp giải:

Tính số chữ số từ trang 1 – 9; 10 – 99; 101 – 999;… Sau đó cộng tất cả lại ta sẽ được đáp số.

Áp dụng các công thức tính:

số số hạng = (số cuối – số đầu) : khoảng cách giữa hai số + 1

Số chữ số từ trang 1 đến trang 9: 1 × 9 = 9 (chữ số)

Số chữ số từ trang 10 đến trang 99: 2 × 90 = 180 (chữ số)

….

Lời giải:

Số chữ số để dùng đánh số trang từ 1 đến 9 là: (9 - 1) : 1 + 1 = 9 (chữ số)

Số chữ số để dánh số trang từ 10 đến 99 là : (99 - 10) : 1 + 1 x 2 = 180 (chữ số)

Số chữ số để dánh số trang từ 100 đến 216 là : (216 - 100) : 1 +1 x 3 = 351 (chữ số)

Từ 1 đến 216 là: 9 + 180 + 351 = 540 (chữ số)

Câu 8: Tìm số liền trước số 9

Phương pháp giải:

- Trên tia số, mỗi số (khác 0) lớn hơn các số ở bên trái nó và bé hơn các số ở bên phải nó.

- Các số trên tia số được sắp xếp theo thứ tự tăng dần.

- Số liền trước của một số kém số đó 1 đơn vị.

 Số liền sau của một số hơn số đó 1 đơn vị.

Lời giải:

Số liền trước của số 9 là số 8

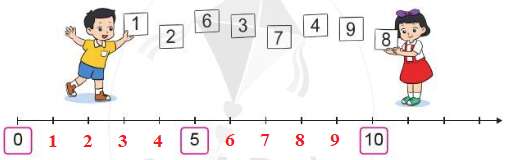
Mở rộng:

Số liền sau của số 9 là số 10

Số liền sau của số 8 là số 9

Số liền trước của số 10 là số 9

Câu 9: Cho hai tia Ox và Oy đối nhau. Vẽ tia Oz sao cho góc xOz = $\frac{4}{9}$ góc xOy .

Phương pháp giải:

a) Hai tia chung gốc Ox và Oy tạo thành một đường thẳng xy gọi là hai tia đối nhau.

- Mỗi điểm trên đường thẳng là gốc chung của hai tia đối nhau.

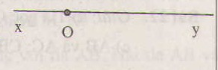
Hình bên: Hai tia Ox và Oy là hai tia đối nhau.

b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Ví dụ:

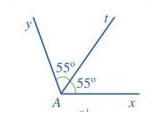
Tia At là tia phân giác của góc xAy vì tia At nằm trong góc xAy và $\widehat{xAt}=\widehat{yAt}(={55}^{\circ })$

Chú ý:

Ta cũng có thể hiểu Om là tia phân giác của góc xOy $\iff \widehat{xOm}=\widehat{yOm}=\frac{1}{2}\widehat{xOy}$

Lời giải:

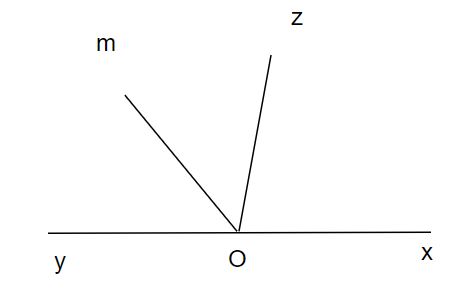
a. Ta có Ox,Oy là 2 tia đối nhau nên $xOy=180^o$

Mặt khác, $xOz=\frac{4}{9}\mathrm{.}xOy=\frac{4}{9}\mathrm{.}180^o=80^o$

Vậy $xOz=80^o$

b. +Trên cùng 1 nửa mặt phẳng bờ xy có 2 tia Oz,Om mà $xOz<xOm(80^o<130^o)$

nên Oz nằm giữa Ox,Om.

 Do đó, $xOz+zOm=xOm$

  =>  $zOm=xOm-xOz=130^o-80^o=50^o$

+ yOm và xOm là 2 góc kề bù => $yOm+xOm=180^o\Rightarrow yOm=180^o-xOm=180^o-130^o=50^o$

+ yOz và xOz là 2 góc kề bù => $yOz+xOz=180^o\Rightarrow yOz=180^o-xOz=180^o-80^o=100^o$

Ta thấy $\{\begin{array}{l}yOm=50^o\\ zOm=50^o\\ yOz=100^o\end{array}$​

nên $yOm=zOm=\frac{yOz}{2}=\frac{100^o}{2}=50^o$=> Om là tia phân giác của góc yOz

Vậy Om là tia phân giác của góc yOz

Câu 10: Cho $A=\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+...+\frac{1}{{50}^2}$. Chứng minh rằng:

a) $A>\frac{1}{4}$

b) $A<\frac{4}{9}$

Phương pháp giải:

Ta có $\frac{1}{a.(a+1)}=\frac{1}{a}-\frac{1}{a+1}$

$$\begin{gathered} \frac{1}{a.(a+1)}+\frac{1}{(a+1)(a+2)}=\frac{1}{a}-\frac{1}{a+1}+\frac{1}{a+1}-\frac{1}{a+2} \\ =\frac{1}{a}-\frac{1}{a+2} \end{gathered}$$

Lời giải:

Ta có $A=\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+...+\frac{1}{{50}^2}$

=> $A>\frac{1}{3^2}+\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{50.51}$

$\Rightarrow A>\frac{1}{9}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+....+\frac{1}{50}-\frac{1}{51}$

$\Rightarrow A>\frac{1}{4}+\left(\frac{1}{9}-\frac{1}{51}\right)$

$\Rightarrow A>\frac{1}{4}+\frac{42}{9.51}>\frac{1}{4}$

Vậy $A>\frac{1}{4}$

b)

Ta có $A=\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+...+\frac{1}{{50}^2}$

$A<{\frac{1}{3}}^2+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{49.50}$

$\Rightarrow A<\frac{1}{9}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+.....+\frac{1}{59}-\frac{1}{50}$

$\Rightarrow A<\frac{4}{9}-\frac{1}{50}<\frac{4}{9}$

Vậy $A<\frac{4}{9}$

Câu 11: Chứng minh biểu thức luôn dương:

M = 2x² - 7x + 9

N = 3x² - 4x + 11

Phương pháp giải:

Bình thương của một số luôn lớn hơn hoặc bằng 0. Vậy để chứng minh biểu thức luôn dương ta biểu diễn biểu thức thành bình thương của 1 số + 1 số lớn hơn 0

Lời giải:

$M=2(x^2-\frac{7}{2}x+\frac{9}{2})$

$=2(x^2-2\cdot x\cdot {\displaystyle \frac{7}{4}}+{\displaystyle \frac{49}{16}}+{\displaystyle \frac{23}{16}})$

$=2{(x-{\displaystyle \frac{7}{4}})}^2+{\displaystyle \frac{23}{8}}>0$

$N=3(x^2-\frac{4}{3}x+\frac{11}{3})$

$=3(x^2-2\cdot x\cdot {\displaystyle \frac{2}{3}}+{\displaystyle \frac{4}{9}}+{\displaystyle \frac{29}{9}})$

$=3{(x-{\displaystyle \frac{2}{3}})}^2+{\displaystyle \frac{29}{3}}>0$

Câu 12: Cách vẽ lá cờ Việt Nam bằng cách chia tỉ lệ trên hình chữ nhật

Phương pháp giải:

Thiết kế chuẩn của quốc kỳ Việt Nam là hình chữ nhật, chiều rộng bằng $\frac{2}{3}$ chiều dài, nền màu đỏ tươi, chính giữa là ngôi sao vàng 5 cánh. Tâm ngôi sao phải trùng với tâm của hình chữ nhật (là giao điểm của 2 đường chéo). Ngoài ra, khoảng cách từ tâm ngôi sao đến đầu mỗi cánh sao phải bằng đúng $\frac{1}{5}$ chiều dài lá cờ. Đường tròn bao ngoài ngôi sao vàng 5 cánh có đường kính bằng $\frac{2}{5}$ chiều dài lá cờ.

Lời giải:

Ví dụ chiều dài lá cờ là 30 đơn vị, thì tỷ lệ kích thước chuẩn của khung và hình ngôi sao 5 cánh sẽ như hình sau:

Chiều dài lá cờ là 30

=> chiều rộng là cờ là $\frac{2}{3}.30=20$

Chiều dài cánh ngôi sao từ tâm tới đầu cánh là $\frac{1}{5}.30=6$

Đường kính đường tròn bao quanh ngôi sao là $\frac{2}{5}.30=12$

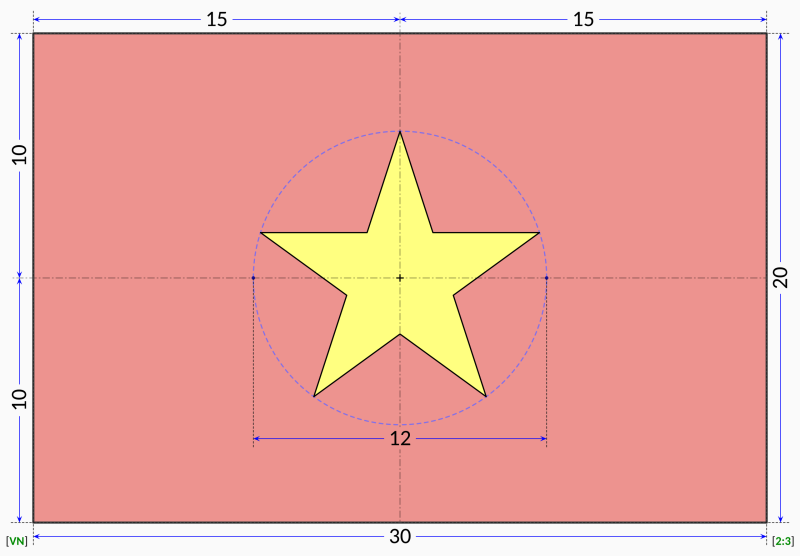
Mở rộng:

Về kích thước, cờ Việt Nam có một số kích thước thông dụng như 60x90cm, 80x120cm, 2x3m, 4x6m, 6x9m ... nhưng chỉ cần đảm bảo đúng tỷ lệ và hình dạng, giữa chiều dài và chiều rộng đảm bảo $\frac{2}{3}$ là được.

Ý nghĩa của lá cờ tổ quốc Việt Nam: “Màu đỏ của lá cờ là màu của cách mạng. Chúng ta giành lấy nền độc lập và giữ nền độc lập bằng máu của nhiều thế hệ dân tộc chúng ta. Ngôi sao vàng là màu của chủng tộc, chủng tộc da vàng, còn 5 cánh của ngôi sao là tựu trung cho sự đoàn kết của dân tộc của 5 lớp người: sĩ, nông, công, thương, binh. Và sự quy tụ đó là của khối đại đoàn kết dân tộc".

Câu 13: Mẹ vuông, con tròn. Mỗi lứa sòn sòn. Đẻ 20 đứa. Là gì?

Phương pháp giải:

Bài toán đố mẹo

Lời giải:

Bao thuốc lá

(Vỏ bao thuốc là là mẹ; điếu thuốc là con, mỗi 1 bao thuốc có 20 điếu thuốc)

Mở rộng:

Có chân mà chẳng biết đi, Quanh năm suốt tháng đứng ì một nơi, Bạn bè chăn chiếu gối thôi, Cho người nằm ngủ thảnh thơi đêm ngày - Là cái gì?

Đáp án: Cái giường

Câu 14: Tìm x biết:

a) 45 - (x + 9) = 6

b) 4.2^x - 3 = 125

Phương pháp giải:

Phương trình có dạng $a^x=b\left(0<a\ne 1\right)$

+) Với $b>0$ ta có $a^x=b\iff x={\log }_{a}b$.

+) Với $b\le 0$ phương trình vô nghiệm.

Lời giải:

a) 45 - (x + 9) = 6

45 - x - 9 = 6

x = 6 + 9 - 45

x = - 30

b) 4.2^x - 3 = 125

4.2^x = 128

2^x = 32 

$x={\log }_2\left(32\right)={\log }_2\left(2^5\right)$

x = 5

Câu 15: Tìm x biết

a, 890 : x = 35 dư 15

b, 648 - 34.x = 444

c, 1482:x + 23 = 80

Phương pháp giải:

a) Số chia = (số bị chia - số dư) : thương

b) Số trừ = số bị trừ - hiệu

Thừa số chưa biết = tích : thừa số đã biết

c) Số hạng chưa biết = tổng - số hạng đã biết

Số chia = số bị chia : thương

Lời giải:

a, 890 : x = 35 dư 15

x = (890 - 15) : 35

x = 875 : 35 = 25

b) 648 - 34.x = 444

34.x = 648 - 444 = 204

x = 204 : 34 = 6

c, 1482:x + 23 = 80

1482:x = 80 - 23 = 57

x = 1482 : 57 = 26

Câu 16: Tính A = 2023 - 2022 + 2021 - 2020 .... + 3 - 2 + 1

Phương pháp giải:

Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1

Lời giải:

A = 2023 - 2022 + 2021 - 2020 .... + 3 - 2 + 1

A = (2023 - 2022) + (2021 - 2020) + .... + (3 - 2) + 1

Đặt B = (2023 - 2022) + (2021 - 2020) + .... + (3 - 2) => A = B + 1

Biểu thức $B$ có số số hạng là: 

${\displaystyle (2023-2):1+1=2022}$ (số hạng)

Số nhóm được lập là: 

${\displaystyle 2022:2=1011}$ (nhóm)

$B=1+1+...+1$    [${\displaystyle 1011}$ số hạng]

$B=1\times 1011=1011$

$\Rightarrow A=1011+1=1012$

Vậy $A=1012$

Câu 17: Chứng minh rằng (7²⁰⁰⁴ + 32).(49¹⁰¹² + 34) chia hết cho 6

Phương pháp giải:

Nhận thấy 32 + 34 = 66 ⋮ 6

Biểu diễn 49¹⁰¹² theo cơ số 7

Lời giải:

(7²⁰⁰⁴ + 32).(49¹⁰¹² + 34)

= ( 7²⁰²⁴ + 32 ). ( ${\left(7^2\right)}^{1012}$ + 34 )

= ( 7²⁰²⁴ + 32 ) . ( 7²⁰²⁴ + 34 )

= 7²⁰²⁴ ( 32 + 34 )

= 7²⁰²⁴ . 66

Ta có 66 ⋮ 6 => 7²⁰²⁴ . 66 ⋮ 6

=> (7²⁰⁰⁴ + 32).(49¹⁰¹² + 34) chia hết cho 6

Mở rộng:

A = 2 + 2² + 2³+ … + 2²⁰⁰ chia hết cho 6

Nhận xét :

Tổng của hai số hạng : 2 + 2² = 2+ 4 = 6

Tổng A có : 200 số hạng có 100 nhóm chứa hai số hạng có tổng 6.

Lời giải:

A = (2 + 2²) + (2³ + 2⁴ ) +…(2¹⁹⁹ + 2²⁰⁰)

A = 6 + 2² (2 + 2² ) +… + 2¹⁹⁸ (2 + 2²)

A = 6 + 2² (6 ) +… + 2¹⁹⁸ (6)

A = 6(1 + 2² +… + 2¹⁹⁸)

Vậy A chia hết cho 6

Câu 18: Cho 3 số x, y, z thỏa mãn x.y.z = 1. Tính giá trị của biểu thức:

Lời giải:

 $M=\frac{1}{1+x+xy}+\frac{1}{1+y+yz}+\frac{1}{1+z+zx}$

Vì x.y.z = 1 nên $x\mathrm{\ne }0;y\mathrm{\ne }0;z\mathrm{\ne }0$

Ta có $\frac{1}{1+x+xy}=\frac{z}{(1+y+yz)xz}=\frac{xz}{z+xz+1}$

Tương tự $\frac{1}{1+y+yz}=\frac{xz}{(1+y+yz)xz}=\frac{xz}{xz+z+1}$

Khi đó $M=\frac{z}{z+xz+1}+\frac{xz}{xz+1+z}+\frac{1}{1+z+xz}=\frac{z+xz+1}{z+zx+1}=1$

Mở rộng:

Biết x.y.z = 1. Tính giá trị của biểu thức:

P = $\frac{x+2xy+1}{x+xy+xz+1}+\frac{y+2yz+1}{y+yz+yx+1}+\frac{z+2zx+1}{z+zx+zy+1}$

Lời giải:

Câu 19: Tính tổng 100 + 97 + 94 +...+ 7 + 4 + 1

Phương pháp giải:

Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1

Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) x số số hạng : 2

Lời giải:

100 + 97 + 94 +...+ 7 + 4 + 1

Ta thấy dãy số trên là dãy số cách đều và khoảng cách là 3 

Số số hạng của dãy là:

(100 - 1) : 3 + 1 = 34 (số)

Tổng của dãy số là:

(100 + 1). 34 : 2 = 1717

Vậy tổng của dãy số trên là 1717.

Mở rộng: Cho dãy số 11 ; 14 ; 17 ; 20 ; …. ; 68

a) Dãy số trên có bao nhiêu số hạng?

b) Nếu ta tiếp tục kéo dài các số hạng của dãy số đó thì số hạng thứ 2007 là số nào?

Bài giải

Lời giải câu a

Dãy số đã cho là dãy số cách đều 3 đơn vị.

Số số hạng của dãy số là

(68 – 11) : 3 + 1 = 20 (số hạng)

Lời giải câu b

• • Số hạng thứ 2 của dãy số là: 14 = 11 + 3 x (2 – 1)
  • Số hạng thứ 3 của dãy số là 17 = 11 + 3 x (3 – 1)
  • Số hạng thứ 4 của dãy số là 20 = 11 + 3 x (4 – 1) 

            ……

Vậy số hạng thứ 2007 của dãy số là 11 + 3 x (2007 – 1) = 6029

Câu 20: Tìm x biết: 2^x+2 + 2^x = 40

Phương pháp giải:

  Với a > 0 và a ≠ 1 ta có a^f(x) = a^g(x) ⇔ f(x) = g(x).

Lời giải:

2^x+2 + 2^x = 40

$2^x\mathrm{.}{2}^2+2^x=40$

$2^x\mathrm{.}4+2^x=40$

$2^x\mathrm{.}(4+1)=40$

$2^x\mathrm{.}5=40$

$2^x=40:5$

$2^x=8$

2^x = 2³

$\Rightarrow x=3$

Mở rộng:

Cách giải một số phương trình mũ đơn giản

a) Đưa về cùng cơ số

b) Đặt ẩn phụ

c) Logarit hóa

d) Đưa về phương trình tích

- Bước 1: Tìm điều kiện xác định (nếu có)

- Bước 2: Biến đổi phương trình về dạng tích $AB=0\iff [\begin{array}{l}A=0\\ B=0\end{array}$

- Bước 3: Giải các phương trình $A=0,B=0$ tìm nghiệm.

- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.

e) Sử dụng bất đẳng thức, tính đơn điệu của hàm số

- Bước 1: Tìm điều kiện xác định.

- Bước 2: Có thể làm một trong hai cách sau:

Cách 1: Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.

Cách 2: Biến đổi phương trình về dạng $f\left(u\right)=f\left(v\right)$ với $f$ là hàm số đơn điệu.

- Bước 3: Nhẩm một nghiệm của phương trình trên.

- Bước 4: Kết luận nghiệm duy nhất của phương trình.

Câu 21: Hai thành phố A và B cách nhau 135km. Lúc 8 giờ sáng 1 người đi ô tô từ A với vận tốc 60km/giờ về phía B. 15 phút sau, 1 người đi xe máy từ B về A với vận tốc 20km/giờ. Hỏi 2 xe gặp nhau lúc mấy giờ? nơi gặp nhau cách A bao nhiêu km?

Phương pháp giải:

Hai vật chuyển động ngược chiều với vận tốc v₁ và v₂, cùng thời điểm xuất phát và cách nhau quãng đường s.

Thời gian để hai vật gặp nhau là: 

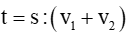
Tổng vận tốc: 

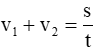
Quãng đường: 

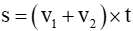
Lời giải:

Đổi: ${\displaystyle 15}$ phút = ${\displaystyle 0,25}$ giờ

Quãng đường người đi xe ô tô đi trước là:

 ${\displaystyle 60\times 0,25=15\left(km\right)}$

Tổng vận tốc ${\displaystyle 2}$ xe là:

 ${\displaystyle 60+20=80}$(km/giờ)

Mất số thời gian để 2 xe gặp nhau là:

 ${\displaystyle (135-15):80=1,5}$(giờ) = ${\displaystyle 1}$ giờ ${\displaystyle 30}$ phút

2 xe gặp nhau lúc:

 ${\displaystyle 8}$ giờ + ${\displaystyle 15}$ phút + ${\displaystyle 1}$ giờ ${\displaystyle 30}$ phút = ${\displaystyle 9}$ giờ ${\displaystyle 45}$ phút

Cách ${\displaystyle A}$ số km là:

 ${\displaystyle 60\times 1,5+15=105\left(km\right)}$

 Đáp số: Gặp nhau lúc: ${\displaystyle 9}$ giờ ${\displaystyle 45}$ phút; Cách ${\displaystyle A}$: ${\displaystyle 105km}$

Câu 22: Vẽ hai góc kề bù $\widehat{xOy}$ và $\widehat{yOz}$ sao cho $\widehat{xOy}={60}^0$

a) Tính $\widehat{yOz}$

Phương pháp giải:

* Tính chất: 2 góc kề bù có tổng số đo là 180 độ.

Định nghĩa: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau. 

Nhận xét: Nếu tia $Oz$ là tia phân giác của góc $xOy$ thì  $\widehat{xOz}=\widehat{yOz}={\displaystyle \frac{\widehat{xOy}}{2}}$

Lời giải:

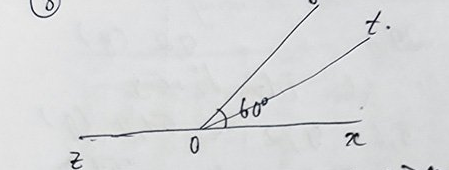
a) Vì góc xOy và góc yOz là 2 góc kề bù nên: góc xOy + góc yOz = 180^o

=> góc yOz = 180^o - góc xOy = 180^o - 60^o = 120^o

b) Vì Ot là tia phân giác của góc xOy nên $\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}.60°=30°$

=> $\widehat{zOt}=\widehat{zOy}+\widehat{yOt}=120°+30°=150°$

Câu 23: Chứng minh  $A=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}$ không phải là số tự nhiên.

Phương pháp giải:

Ta chứng minh biểu thức 

Lời giải:

Để quy đồng ta sẽ chọn mẫu chung tích các thừa số nguyên tố chung và riêng (hay ta tìm BCNN của mẫu)

Ta chọn mẫu chung là 2⁶.3.5.7.9.99

Gọi k₁; k₂; …; k₁₀₀ là các thừa số phụ tương ứng, do đó A có dạng:

A = $\frac{k_1+k_2+...+k_{100}}{2^6.3.5.7.9....99}$

Trong 100 phân số của tổng A chỉ có phân số duy nhất $\frac{1}{64}$ chứa 2⁶ nên trong các thừa số phụ chỉ có k₆₄ là số lẻ, còn lại các thừa số phụ đều là số chẵn.

Nên tử số không chia hết cho 2, trong khi mẫu số chia hết cho 2.

Do đó phân số A không phải là số tự nhiên.

Câu 24: Tìm x: ${\displaystyle x\times 0,125=\frac{3,6+2,8}{8}}$

Phương pháp giải:

Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết

Chú ý: Để thực hiện phép chia hai phân số, ta: Lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Lời giải:

${\displaystyle x\times 0,125=\frac{3,6+2,8}{8}}$

${\displaystyle \Rightarrow x\times \frac{1}{8}=\frac{6,4}{8}}$

${\displaystyle \Rightarrow x\times \frac{1}{8}=\frac{4}{5}}$

${\displaystyle \Rightarrow x=\frac{4}{5}:\frac{1}{8}}$

${\displaystyle \Rightarrow x=\frac{32}{5}}$

Vậy ${\displaystyle x=\frac{32}{5}}$

Câu 25: Tính nhanh: 58x42 + 32x8 + 5x16

Phương pháp giải:

- Bước 1: Tách các biểu thức theo từng tích trong phép tính

- Bước 2: Quan sát để tìm ra thừa số chung cùng xuất hiện ở tất cả các tích.

- Bước 3: Đưa thừa số vừa tìm được ra ngoài (trở thành thừa số chung)

Lời giải:

58×42 + 32×8 + 5×16

= 58×42 + 32×8 + 5×2×8

= 58×42 + 32×8 + 10×8

= 58×42 + 8×(32 + 10)

= 58×42 + 8×42

= 42×(58 + 8)

= 42×66

= 2772