Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 13)
a) Tìm tọa độ hai điểm A, B. Tìm m, n biết (d) đi qua hai điểm A, B.
b) Tính độ dài đường cao OH của tam giác OAB. (điểm O là gốc tọa độ).
Lời giải:
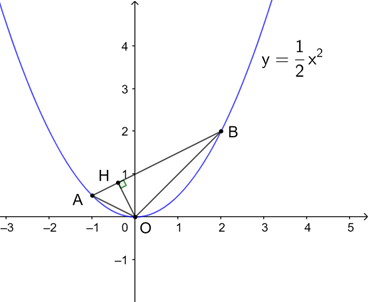
a) Tung độ hai điểm A, B Î (P) là:
Vậy .
Đường thẳng (d) đi qua hai điểm có phương trình là:
(d):
Vậy là các giá trị cần tìm.
b) Ta có:
a) Tìm tọa độ hai điểm A, B.
b) Tìm m, n biết (d) đi qua hai điểm A, B.
Lời giải:
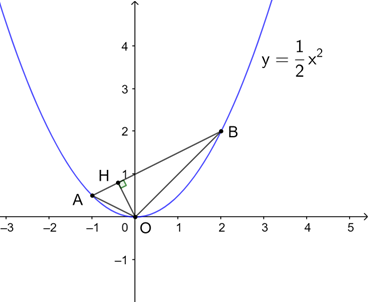
a) Tung độ hai điểm A, B Î (P) là:
.
Vậy .
b) Đường thẳng (d) đi qua hai điểm có phương trình là:
(d):
Vậy là các giá trị cần tìm.
Câu 3: Cho tan a + cot a = m. Tìm m để tan2 a + cot2 a = 7.
Lời giải:
Ta có: tan2 a + cot2 a = 7
<=> (tan a + cot a)2 − 2tan a.cot a = 7
<=> m2 − 2.1 = 7
<=> m2 = 9
<=> m = ± 3.
Vậy m = ± 3 là các giá trị cần tìm của m.
Câu 4: Cho tan a + cot a = m. Tính tan3 a + cot3 a theo m.
Lời giải:
Ta có:
• tan2 a + cot2 a
= (tan a + cot a)2 − 2tan a.cot a
= m2 − 2.1
= m2 − 2
• tan3 a + cot3 a
= (tan a + cot a)(tan2 a − tan a.cot a + cot2 a)
= m.(m2 − 2 − 1)
= m.(m2 − 3)
= m3 − 3m
a) Tìm điều kiện của x để A có nghĩa.
b) Rút gọn A.
c) Tìm x để .
d) Tìm x để biểu thức A có giá trị nguyên.
e) Tìm giá trị của A khi x2 − 9 = 0.
Lời giải:
a) Ta có
ĐKXĐ: .
b)
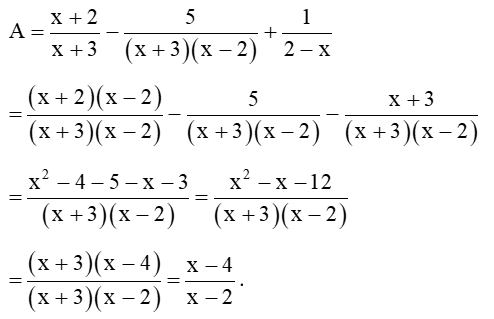
c) Để thì:
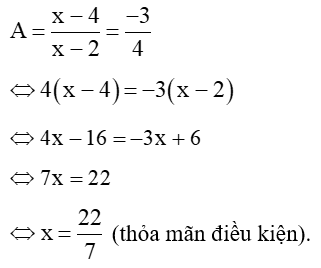
d) Ta có:
Vì 1 Î ℤ nên để A Î ℤ thì
Þ x − 2 Î Ư (2) = {±1; ±2}
Þ x Î {0; 1; 3; 4}.
Vậy để A nhận giá trị nguyên thì x Î {0; 1; 3; 4}.
e) x2 − 9 = 0
=> (x + 3)(x − 3) = 0
Thay vào biểu thức A, ta có:
.
Câu 6: Cho biểu thức . Tìm x để .
Lời giải:
Ta có
ĐKXĐ:
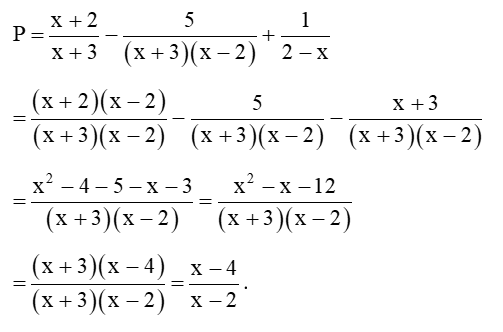
Để thì:
(thỏa mãn điều kiện).
Vậy với thì .
Lời giải:
Gọi số có 3 chữ số cần tìm là .
Ta có
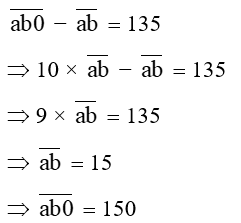
Vậy số cần tìm là 150.
Lời giải:
Gọi số có 3 chữ số cần tìm là .
Ta có
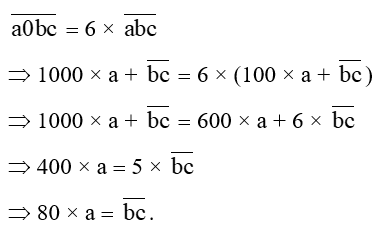
Với a là số tự nhiên thỏa mãn 1 a 9 thì:
• Với a = 1 = 80 (thỏa mãn)
=> = 180.
• Với a = 2 => = 160 (loại vì là số có 2 chữ số).
• Với a > 2 => > 160 (loại vì là số có 2 chữ số).
Vậy số cần tìm là 180.
Lời giải:
(*)
Đặt thì phương trình (*) trở thành:
<=> (9t − 1)(t − 1) = 0
• Với
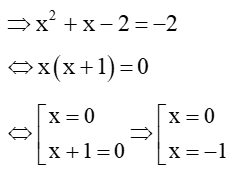
• Với
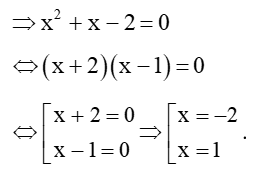
Vậy nghiệm của phương trình là x Î {−2; −1; 0; 1}.
Câu 10: Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.
Lời giải:
Giả sử a2 + b2 + c2 ≥ ab + bc + ca
=> 2(a2 + b2 + c2) ≥ 2(ab + bc + ca)
=> 2a2 + 2b2 + 2c2 ≥ 2ab + 2bc + 2ca
=> (a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) ≥ 0
=> (a − b)2 + (b − c)2 + (c − a)2 ≥ 0
Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 ≥ 0 nên suy ra
(a − b)2 + (b − c)2 + (c − a)2 ≥ 0 (luôn đúng).
Vậy a2 + b2 + c2 ≥ ab + bc + ca (đpcm).
Câu 11: Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh a = b = c.
Lời giải:
Ta có: a2 + b2 + c2 = ab + bc + ca
=> 2(a2 + b2 + c2) = 2(ab + bc + ca)
=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca
=> (a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) = 0
=> (a − b)2 + (b − c)2 + (c − a)2 = 0
Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 ≥ 0 nên suy ra
(đpcm).
Lời giải:
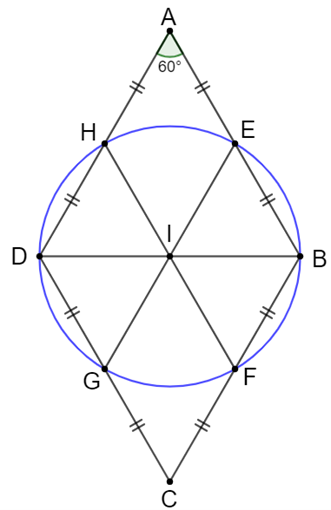
Gọi I là trung điểm của BD (1)
Xét tam giác ABD có và AB = AD nên ∆ABD đều Þ AB = BD
+) E và I là trung điểm của BA và BD nên EI là đường trung bình của ∆BAD
(2)
+) Tương tự (3)
Chứng minh tương tự ta có tam giác BDC đều và (4)
Mặt khác (5)
Từ (1), (2), (3), (4) và (5) suy ra IB = ID = IE = IH = IG = IF
Vậy 5 điểm E, F, G, H, B, D cùng thuộc đường tròn tâm I, đường kính BD.
Lời giải:
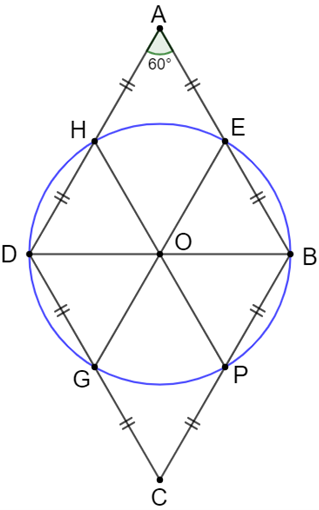
Gọi O là trung điểm của BD (1)
Xét tam giác ABD có và AB = AD nên ∆ABD đều Þ AB = BD
+) E và O là trung điểm của BA và BD nên EO là đường trung bình của ∆BAD
(2)
+) Tương tự (3)
Chứng minh tương tự ta có tam giác BDC đều và (4)
Mặt khác (5)
Từ (1), (2), (3), (4) và (5) suy ra OB = OD = OE = OH = OG = OP
Vậy 5 điểm E, P, G, H, B, D cùng thuộc đường tròn tâm O, bán kính BO.
Lời giải:
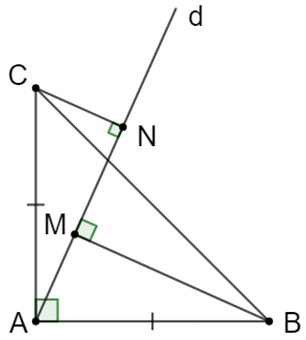
Xét tam giác ACN vuông tại N
(1)
Mà (2)
Từ (1) và (2) suy ra (hai góc cùng phụ với )
Xét ∆NCA và ∆MAB vuông tại N và M có:
(cmt)
AC = BA (hai cạnh góc vuông của tam giác vuông cân)
Do đó ∆NCA = ∆MAB (cạnh huyền – góc nhọn)
Vậy ∆BAM = ∆CAN (đpcm).
a) ∆BAM = ∆CAN.
b) MN = BM + CN.
Lời giải:
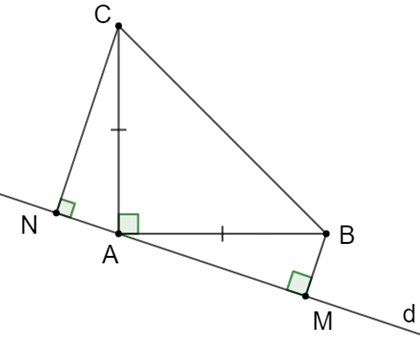
a) Xét tam giác ACN vuông tại N
(1)
Mà (2)
Từ (1) và (2) suy ra (hai góc cùng phụ với )
Xét ∆NCA và ∆MAB vuông tại N và M có:
(cmt)
AC = BA (gt)
=> ∆NCA = ∆MAB (cạnh huyền – góc nhọn)
Vậy ∆BAM = ∆CAN (đpcm).
b) ∆NCA = ∆MAB => BM = AN và CN = AM (các cặp cạnh tương ứng bằng nhau)
=> MN = MA + AN = CN + BM
Vậy MN = BM + CN (đpcm)
Câu 16: Số nghiệm của phương trình cos 2x + 3sin x − 2 = 0 trên khoảng (0; 20π) là bao nhiêu?
Lời giải:
cos 2x + 3sin x − 2 = 0
<=> 1 − 2sin2 x + 3sin x − 2 = 0
<=> − 2sin2 x + 3sin x − 1 = 0
<=> 2sin2 x − 3sin x + 1 = 0
<=> (2sin x − 1)(sin x − 1) = 0
+) TH1: sin x = 1
Với x (0; 20π)
=> 0 k 9 (k ℤ)
Vậy TH1 cho 10 nghiệm x thỏa mãn
+) TH2:
Với x (0; 20π)
Vậy TH2 cho 20 nghiệm x thỏa mãn.
Vậy có 30 nghiệm của x thỏa mãn phương trình.
Câu 17: Giải phương trình: cos 2x + 3sin x − 2 = 0.
Lời giải:
cos 2x + 3sin x − 2 = 0
<=> 1 − 2sin2 x + 3sin x − 2 = 0
<=> − 2sin2 x + 3sin x − 1 = 0
<=> 2sin2 x − 3sin x + 1 = 0
<=> (2sin x − 1)(sin x − 1) = 0
• TH1: sin x = 1
• TH2:
Vậy là tập nghiệm của phương trình với (k Î ℤ).
Câu 18: Tính sin x, cos x, tan x, cot x biết .
Lời giải:
Lại có:
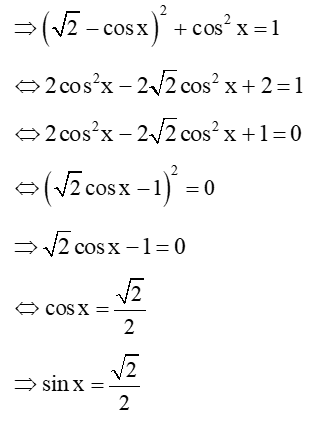
Khi đó .
Câu 19: Cho . Hãy tính: A = sin x.cos x.
Lời giải:
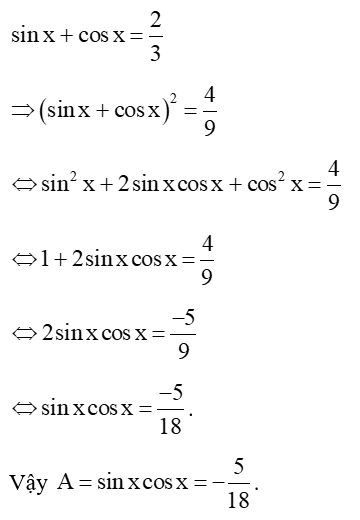
Lời giải:
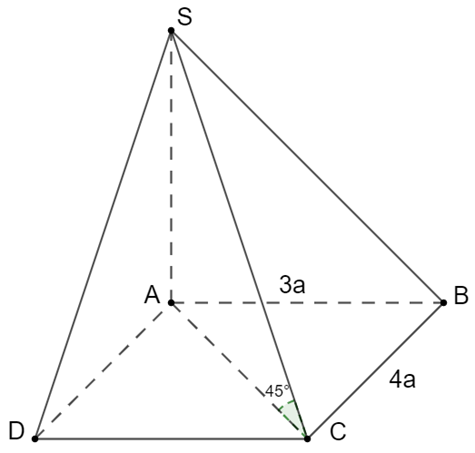
Ta có SA (ABCD)
.
.
Trong ∆SAC vuông tại A
.
Khi đó, thể tích khối chóp S.ABCD là:
Lời giải:
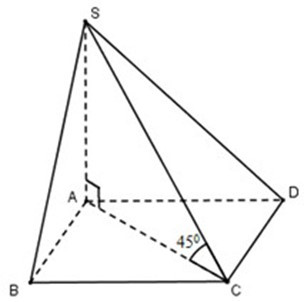
Ta có SA (ABCD) => SA AC
=> ∆SAC vuông cân tại A
.
Xét tam giác vuông ABC ta có:
.
Khi đó, thể tích khối chóp S.ABCD là:
Lời giải:
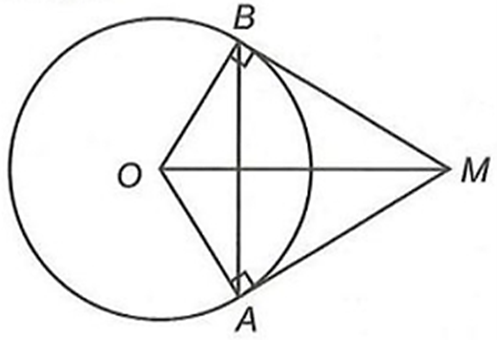
Vì MA và MB là tiếp tuyến của đường tròn (O) nên ta có MA = MB (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác MAB cân tại M.
Mặt khác nên tam giác MAB đều.
Theo giả thiết có chu vi tam giác ABM là:
3.AB = 18 <=> AB = 6 (cm)
Lời giải:
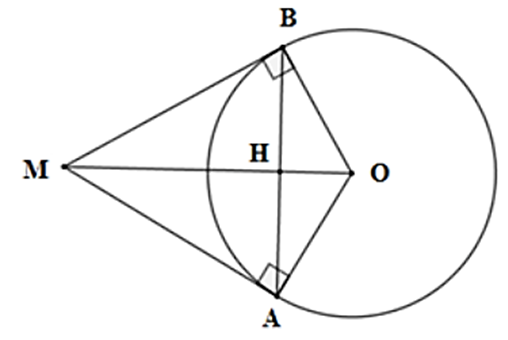
Vì MA và MB là tiếp tuyến của đường tròn (O) nên ta có MA = MB (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác MAB cân tại M
Mặt khác nên tam giác MAB đều
Theo giả thiết có chu vi tam giác ABM là:
3.AB = 24 <=> AB = 8 (cm)
=> MA = MB = AB = 8 cm.
Lại có (tính chất hai tiếp tuyến cắt nhau).
Xét tam giác vuông MAO có:
Câu 24: A \ B được gọi là phần bù của B trong A khi nào?
A. A B;
B. B A;
C. A B;
D. A B.
Lời giải:
Theo lý thuyết khi B ⊂ A thì A \ B được gọi là phần bù của B trong A, kí hiệu là CAB.
Vậy ta chọn đáp án B.
Câu 25: . Dấu “=” xảy ra khi nào?
Lời giải:
Dấu “=” xảy ra khi A = B.
b) Tìm ƯC của 10 và 20.
Lời giải:
a) Ta có: 4 = 22; 6 = 2.3
BCNN(4, 6) = 22.3 = 12
=> BC(4, 6) = B(12) = {0; 12; 24; 36; …}.
b) Ta có: 10 = 2.5; 20 = 22.5
=> ƯCLN(10, 20) = 2.5 = 10
=> ƯC(10, 20) = Ư(10) = {1; 2; 5; 10}.
Câu 27: Tìm ƯC thông qua tìm ƯCLN: 10; 20 và 70.
Lời giải:
Ta có: 10 = 2.5; 20 = 22.5; 70 = 2.5.7
ƯCLN(10, 20, 70) = 2.5 = 10
=> ƯC(10, 20, 70) = Ư(10) = {1; 2; 5; 10}.
Lời giải:
Để tứ giác ABCD là hình bình hành thì:
Vậy D(−2; 1).
Lời giải:
Để tứ giác ABCD là hình bình hành thì:
Vậy D(2; −4).
Câu 30: Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn:
.
Lời giải:
(Với I là trung điểm của AC)
<=> 2MI = BA.
Vậy M thuộc đường tròn tâm I đường kính BA với I là trung điểm của AC.
Câu 31: Cho tam giác ABC. Tìm tập hợp các điểm M trong trường hợp sau:
.
Lời giải:
Ta có:
(trái với giả thiết).
Vậy không có điểm M nảo thỏa mãn.
Lời giải:
Để phương trình có 2 nghiệm dương phân biệt thì
Đặt
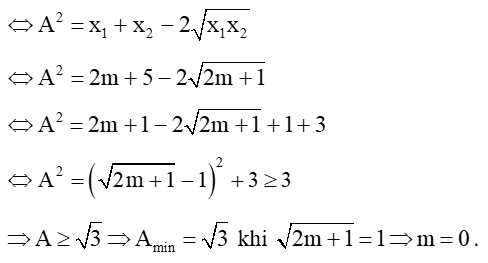
Vậy GTNN của bằng khi m = 0.
Câu 33: Cho phương trình: x2 − 2(m − 1)x + 2m − 5 = 0 (1)
a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biết với mọi m.
b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 < 2 < x2.
Lời giải:
a) Ta thấy:
Do đó phương trình luôn có hai nghiệm phân biệt với mọi m thực
b) Áp dụng định lý Vi-ét với x1, x2 là hai nghiệm của phương trình thì:
Khi đó, để x1 < 2 < x2 Û (x1 − 2)(x2 − 2) < 0
<=> x1x2 − 2(x1 + x2) + 4 < 0
<=> 2m − 5 − 4(m − 1) + 4 < 0
<=> − 2m + 3 < 0
Vậy là giá trị của m thỏa mãn.
Câu 34: So le ngoài là như thế nào? Lấy ví dụ.
Lời giải:
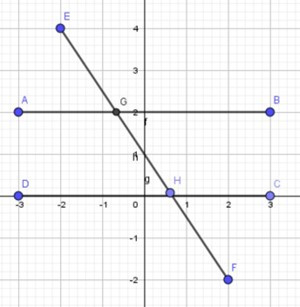
Hai góc so le trong là hai góc về hai phía đối vớí cát tuyến và nằm bên ngoài của hai đường thẳng song đó.
Ví dụ: .
Lời giải:
- Cặp góc so le trong cùng phía là những góc nằm ở vị trí so le nhau nằm trong hình và cùng nằm ở 1 đường thẳng.
- Góc so le ngoài cùng phía là những góc nằm ở vị trí so le nhau nằm trong hình và cùng nằm trên 1 đường thẳng.
- Cặp góc so le trong là những góc nằm ở vị trí so le nhau nằm trong hình và cùng nằm ở 1 đường thẳng.
- Cặp góc đồng vị là những góc nằm ở vị trí giống nhau ở hai đường thẳng song song.
Câu 36: Có bao nhiêu đường tròn đi qua ba điểm thẳng hàng?
A. Vô số đường tròn;
B. Một đường tròn;
C. Hai đường tròn;
D. Không có đường tròn nào.
Lời giải:
Không có đường tròn đi qua ba điểm thẳng hàng.
Vậy đáp án đúng là D.
Câu 37: Có bao nhiêu đường tròn đi qua ba điểm không thẳng hàng?
A. Vô số đường tròn;
B. Một đường tròn;
C. Hai đường tròn;
D. Không có đường tròn nào.
Lời giải:
Có một và chỉ một đường tròn đi qua 3 điểm phân biệt không thẳng hàng.
Vậy đáp án đúng là B.
Lời giải:
(d): y = (m + 1)x + 2m − 3
= mx + x + 2m − 3
= m(x + 2) + x – 3.
Điểm cố định mà (d) luôn đi qua có tọa độ là:
Vậy điểm cố định cần tìm có tọa độ là (−2; −5).
Câu 39: Tìm điểm cố định mà đồ thị hàm số y = (m − 1)x + 2m − 3 luôn đi qua
Lời giải:
(d): y = (m − 1)x + 2m − 3
= mx − x + 2m − 3
= m(x + 2) − x – 3.
Điểm cố định mà (d) luôn đi qua có tọa độ là:
Vậy điểm cố định cần tìm có tọa độ là (−2; −1).
Câu 40: Tìm điều kiện của x để biểu thức là phân thức.
Lời giải:
Ta có .
Ta có: (x − 2)(x + 2) ≠ 0
.
Vậy điều kiện xác định của phân thức là x ≠ ± 2.
Câu 41: Cho 6 chữ số 2, 3, 4, 6, 7, 9. Lấy 3 chữ số lập thành số a. Có bao nhiêu số a < 400?
Lời giải:
Chọn chữ số hàng trăm có 2 cách: {2; 3}.
Chọn chữ số hàng chục có: 5 cách.
Chọn chữ số hàng đơn vị có: 4 cách.
Vậy lập được 2.5.4 = 40 số thỏa mãn yêu cầu bài toán.
Câu 42: Cho sáu chữ số: 2, 3, 5, 6, 7, 9.
a) Có bao nhiêu số có ba chữ số, các chữ số trong mỗi số đều khác nhau, được lập thành từ các chữ số trên?
b) Trong các số dược thành lập có bao nhiêu số nhỏ hơn 400? Bao nhiêu số là số lẻ? Bao nhiêu số chia hết cho 5?
Lời giải:
a) Để lập được số có ba chữ số với các chữ số trong mỗi số đều khác nhau thì:
• Chọn chữ số hàng trăm có: 6 cách.
+ Chọn chữ số hàng chục có: 5 cách.
+ Chọn chữ số hàng đơn vị có: 4 cách.
Vậy có: 6.5.4 = 120 số thỏa mãn.
b) • Số có ba chữ số nhỏ hơn 400 với các chữ số khác nhau.
+ Chọn chữ số hàng trăm có 2 cách: {2; 3}.
+ Chọn chữ số hàng chục có: 5 cách.
+ Chọn chữ số hàng đơn vị có: 4 cách.
Vậy lập được 2.5.4 = 40 số thỏa mãn yêu cầu bài toán.
• Số lẻ có ba chữ số với các chữ số khác nhau.
+ Chọn chữ số hàng đơn vị có 4 cách: {3; 5; 7; 9}.
+ Chọn chữ số hàng chục có: 5 cách.
+ Chọn chữ số hàng đơn vị có: 4 cách.
Vậy lập được 4.5.4 = 80 số thỏa mãn yêu cầu bài toán.
• Số có ba chữ số chia hết cho 5 với các chữ số khác nhau.
+ Chọn chữ số hàng đơn vị có 1 cách: {5}.
+ Chọn chữ số hàng chục có: 5 cách.
+ Chọn chữ số hàng đơn vị có: 4 cách.
Vậy lập được 1.5.4 = 20 số thỏa mãn yêu cầu bài toán.
Lời giải:
Gọi số có 6 chữ số khác nhau cần tìm là .
Ta có: 8 = 1 + 2 + 5 = 1 + 3 + 4.
Vậy có 2 cách chọn nhóm 3 số để làm các số hàng chục, hàng trăm, hàng nghìn.
Ứng với 1 bộ số có 3! = 6 cách lập ra số
Chọn ra các số còn lại a, b, f là chọn 3 trong 6 số còn lại có tính đến thứ tự, tức là có cách chọn.
Vậy ứng với 1 bộ số ở trên, ta có thể lập được 6.120 = 720 số.
Vậy có tất cả 720.2 = 1440 số thảo mãn yêu cầu bài toán.
Lời giải:
Đỉnh của parabol là nên theo bài ra ta có hệ phương trình:
Vậy parabol cần tìm là: y = x2 − 2x − 24.
Lời giải:
Theo bài ra ta có hệ phương trình:
Vậy parabol cần tìm là (p): y = x2 − x + 1.
(d1): y = ax + b (a ≠ 0);
(d2): y = a'x + b' (a' ≠ 0);
(d1) và (d2) song song, cắt nhau, trùng nhau khi nào?
Lời giải:
• Để (d1) và (d2) song song suy ra a = a' và b ≠ b'.
• Để (d1) và (d2) cắt nhau suy ra a ≠ a'.
• Để (d1) và (d2) trùng nhau suy ra a = a' và b = b'.
Câu 47: Tìm dư trong phép chia 325 cho 9.
Lời giải:
Ta có: 325 = 9 × 36 + 1.
Vậy phép chia của 325 cho 9 có thương là 36 và dư là 1.
Câu 48: Trong khoảng từ 160 đến 325 có bao nhiêu số chia hết cho 9?
Lời giải:
Số chia hết cho 9 có dạng 9k (với k Î ℤ).
Do số đó thuộc khoảng từ 160 đến 325 nên ta có:
160 < 9k < 325
<=> 18 k 39 (với k ℤ).
Vậy trong khoảng từ 160 đến 325 có 22 số chia hết cho 9.
Câu 49: Tìm số hạng thứ 8 trong khai triển (1 − 2x)12.
Lời giải:
Ta có .
Số hạng thứ 8 theo lũy thừa tăng dần tương ứng với k = 7 là:
.
Vậy số hạng cần tìm là .
Câu 50: Hệ số của số hạng thứ 8 trong khai triển nhị thức Niu-tơn (2 + 3x)14.
Lời giải:
Ta có .
Số hạng thứ 8 theo lũy thừa tăng dần tương ứng với k = 7 là :
.
Vậy hệ số cần tìm là .
Câu 51: Cho hàm số y = (m − 1)x + 2 có đồ thị là đường thẳng (d).
a) Tìm m biết (d) đi qua điểm M(2; 1).
b) Viết phương trình của đường thẳng (d') đi qua điểm B(1; 3) và cắt trục tung tại điểm có tung độ bằng 5. Tìm tọa độ giao điểm của (d) và (d') đã tìm được.
Lời giải:
a) Để đường thẳng (d) đi qua điểm M(2; 1) nên ta có:
(m − 1).2 + 2 = 1
<=> 2m − 2 + 2 = 1
<=> 2m = 1
b) Đường thẳng d' có dạng (d'): ax + b (a ≠ 0).
Theo bài ra ta có hệ phương trình: .
Vậy đường thẳng (d') cần tìm là (d'): y = −2x + 5.
Lời giải:
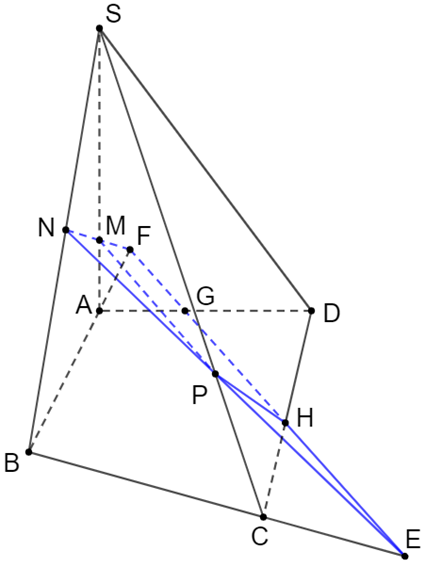
Lấy F và E lần lượt là giao điểm của NM với AB và NP với BC.
Lấy G và H lần lượt là giao điểm của FE với AD và CD.
Vậy giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) là giao tuyến của mặt phẳng (NME) với mặt phẳng (ABCD), tức là GH.
Lời giải:
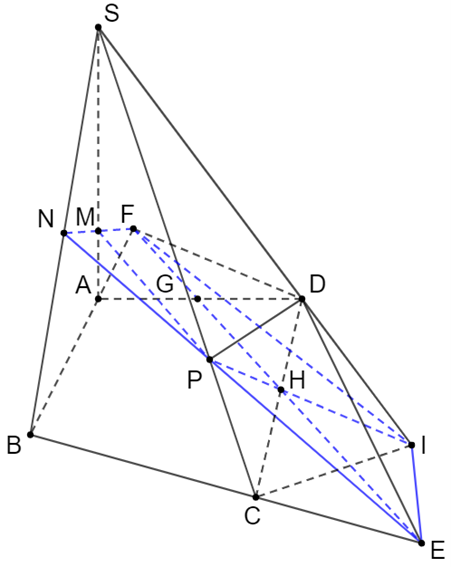
Lấy F và E lần lượt là giao điểm của NM với AB và NP với BC.
Lấy G và H lần lượt là giao điểm của FE với AD và CD.
Lấy I là giao điểm của PH và SD.
Vậy giao điểm của SD và (MNP) là giao điểm của SI và (NEIF), tức là I.
Lời giải:
Người đó làm 12 giờ thì làm được số sản phẩm là:
50 × 12 : 8 = 75 (sản phẩm)
Đáp số: 75 sản phẩm.