Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 57)
Câu 1: Tìm số nguyên dương n, biết: 16 ≤ 8n ≤ 64.
Lời giải:
Ta có 16 ≤ 8n ≤ 64.
Suy ra 24 ≤ (23)n ≤ 26.
Do đó 24 ≤ 23n ≤ 26.
Vì vậy 4 ≤ 3n ≤ 6.
Suy ra .
Mà n là số nguyên dương.
Do đó n = 2.
Vậy n = 2 thỏa mãn yêu cầu bài toán.
a) AD = AI.
b) BE = 2CI.
c) ∆ABD = ∆ACI.
d) BE = 2BD.
Lời giải:
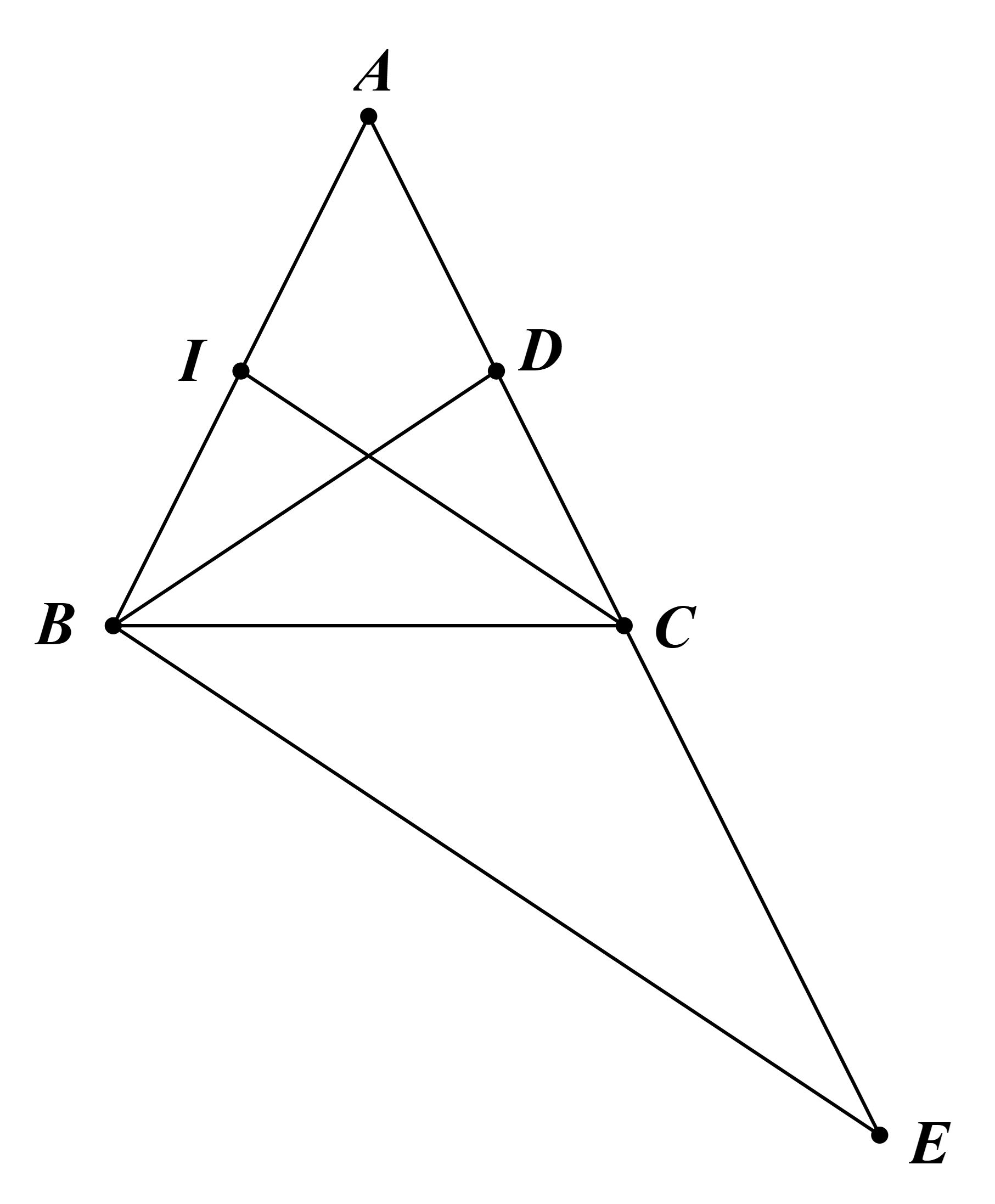
a) Tam giác ABC có BD là đường trung tuyến.
Suy ra D là trung điểm AC.
Do đó AC = 2AD (1)
Lại có I là trung điểm AB (giả thiết).
Suy ra AB = 2AI (2)
Ta có AB = AC (giả thiết) (3)
Từ (1), (2), (3), suy ra 2AD = 2AI.
Vậy AD = AI.
b) Tam giác ABE có C, I lần lượt là trung điểm của AE, AB.
Suy ra CI là đường trung bình của tam giác ABE.
Vậy BE = 2CI.
c) Xét ∆ABD và ∆ACI, có:
AB = AC (giả thiết);
AD = AI (kết quả câu a);
là góc chung.
Vậy ∆ABD = ∆ACI (c.g.c).
d) Ta có BD = CI (∆ABD = ∆ACI).
Mà BE = 2CI (kết quả câu b).
Vậy BE = 2BD.
Câu 3: Chứng minh các biểu thức sau không phụ thuộc vào α:
A = (tanα + cotα)2 – (tanα – cotα)2.
B = sin6α + cos6α + 3sin2α.cos2α.
Lời giải:
⦁ A = (tanα + cotα)2 – (tanα – cotα)2.
= (tanα + cotα – tanα + cotα)(tanα + cotα + tanα – cotα).
= 2cotα.2tanα.
= 4.1 = 4.
⦁ B = sin6α + cos6α + 3sin2α.cos2α.
= (sin2α)3 + (cos2α)3 + 3sin2α.cos2α.
= (sin2α + cos2α).(sin4α – sin2α.cos2α + cos4α) + 3sin2α.cos2α.
= (sin2α + cos2α)2 – 2sin2α.cos2α – sin2α.cos2α + 3sin2α.cos2α.
= 12 = 1.
Vậy ta có điều phải chứng minh.
Lời giải:
Cho quả cân 1 kg lên bàn cân, chia 5 kg gạo vào 2 đĩa sao cho cân thăng bằng.
Khi đó bên cân nào không có quả cân 1 kg thì bên cân đó có 3 kg gạo.
Lời giải:
Số học sinh chỉ thích môn bóng đá là: 35 – 15 = 20 (học sinh).
Số học sinh chỉ thích môn bóng chuyền là: 20 – 15 = 5 (học sinh).
Số học sinh lớp 10A là: 20 + 5 + 15 = 40 (học sinh).
Lời giải:
Gọi a (con), b (con) lần lượt là số con chó và số con gà (a, b ∈ ℕ*, a, b < 40).
Theo đề, ta có hệ phương trình:
(thỏa mãn).
Vậy có 16 con chó và 24 con gà.
Lời giải:
Sau khi ăn hết một nửa số gạo, số gạo còn lại đủ ăn trong:
40 : 2 = 20 (ngày)
1 học sinh ăn hết số gạo còn lại trong số ngày là:
120 × 20 = 2 400 (ngày)
Tổng số học sinh ăn số gạo còn lại trong 12 ngày là:
2400 : 12 = 200 (người)
Trường đó có thêm số học sinh là:
200 − 120 = 80 (học sinh)
Đáp số: 80 học sinh.
Câu 8: Phân tích đa thức thành nhân tử: (x2 – x)2 + 5(x2 – x) – 14.
Lời giải:
Ta có (x2 – x)2 + 5(x2 – x) – 14
= (x2 – x)2 – 2(x2 – x) + 7(x2 – x) – 14
= (x2 – x)(x2 – x – 2) + 7(x2 – x – 2)
= (x2 – x – 2)(x2 – x + 7).
Câu 9: Số tập con của tập hợp A = {x ∈ ℝ | 3(x2 + x)2 – 2x2 – 2x = 0} là bao nhiêu?
Lời giải:
Ta có 3(x2 + x)2 – 2x2 – 2x = 0.
⇔ 3(x2 + x)2 – 2(x2 + x) = 0.
⇔ (x2 + x)[3(x2 + x) – 2] = 0.
Vì vậy .
Vậy số tập con của tập A là 23 = 8 tập con.
Lời giải:
Đổi: .
Trên thực tế hai xã cách nhau số km là:
(km).
Đáp số: 12 km.
Lời giải:
Ta có mx2 – (3m + 2)x + 1 = 0 (1)
Trường hợp 1: m = 0.
Thế m = 0 vào (1), ta được: .
Suy ra nhận m = 0.
Trường hợp 2: m ≠ 0.
∆ = (3m + 2)2 – 4m = 9m2 + 12m + 4 – 4m = 9m2 + 8m + 4.
.
Suy ra phương trình (1) luôn có 2 nghiệm phân biệt, với mọi m.
Kết hợp cả 2 trường hợp, ta thu được phương trình đã cho luôn có nghiệm với mọi giá trị của m.
Lời giải:
Gọi số quả cam trong sọt là a (a ∈ ℕ*).
Suy ra a ∈ BC(6; 10; 12; 14) và 200 ≤ a ≤ 600.
Ta có 6 = 2.3; 10 = 2.5; 12 = 22.3 và 14 = 2.7.
Suy ra BCNN(6; 10; 12; 14) = 22.3.5.7 = 420.
Khi đó a ∈ BC(420) = {0; 420; 840; ...}.
Vì 200 ≤ a ≤ 600 nên a = 420.
Vậy trong sọt có 420 quả cam.
Câu 13: Rút gọn biểu thức: 2x(x – 4)2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)2 – (x – 1)2.
Lời giải:
Ta có 2x(x – 4)2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)2 – (x – 1)2
= 2x(x2 – 8x + 16) – (x + 5)(x2 – 4) + 2(x2 + 10x + 25) – (x2 – 2x + 1)
= 2x3 – 16x2 + 32x – (x3 – 4x + 5x2 – 20) + 2x2 + 20x + 50 – x2 + 2x – 1
= (2x3 – x3) + (–16x2 – 5x2 + 2x2 – x2) + (32x + 4x + 20x + 2x) + (20 + 50 – 1)
= x3 – 20x2 + 58x + 69.
Câu 14: Cho biết tích của hai số tự nhiên n và m là 36. Mỗi tích n.(–m) và (–n).(–m) bằng bao nhiêu?
Lời giải:
Vì tích của hai số tự nhiên n và m là 36 nên n.m = 36.
Ta có:
⦁ n.(–m) = –(n.m) = –36.
⦁ (–n).(–m) = n.m = 36.
Vậy n.(–m) = –36 và (–n).(–m) = 36.
Câu 15: Trong các số thập phân 86,42; 86,422; 686,42; 86,642. Số thập phân lớn nhất là
A. 86,42.
B. 86,422.
C. 686,42.
D. 86,642.
Lời giải:
Đáp án đúng là: C
Ta có 86 < 686.
Do đó số có phần nguyên là 686 là số lớn nhất.
Vậy ta chọn phương án C.
Câu 16: Tìm m để parabol (P): y = x2 – 2mx + m + 3 có đỉnh nằm trên đường thẳng (d): y = x + 2.
Lời giải:
Cho S là đỉnh của parabol, khi đó:
• .
• .
Do đó .
Để S nằm trên (d) thì –m2 + m + 3 = m + 2
⇔ m2 = 1 ⇔ m = ± 1.
Vậy m = ± 1.
Lời giải:
Mua 1 kg đường phải trả số tiền là:
85 000 : 5 = 17 000 (đồng)
Mua 3,5 kg đường phải trả số tiền là:
17 000 × 3,5 = 59 500 (đồng)
Mua 3,5 kg đường phải trả ít hơn mua 5kg đường cùng loại số tiền là:
85 000 – 59 500 = 25 500 (đồng)
Đáp số: 25 500 đồng.
Câu 18: Chứng minh rằng với mọi số thực b, c, ta có: (b + c)2 ≤ 2(b2 + c2).
Lời giải:
Ta có (b + c)2 ≤ 2(b2 + c2).
⇔ b2 + 2bc + c2 ≤ 2b2 + 2c2.
⇔ b2 – 2bc + c2 ≥ 0.
⇔ (b – c)2 ≥ 0, luôn đúng với mọi b, c ∈ ℝ.
Dấu “=” xảy ra ⇔ b = c.
Vậy ta có điều phải chứng minh.
Câu 19: Cho a ≠ b ≠ c thỏa mãn a2(b + c) = b2(c + a) = 2012. Tính M = c2(a + b).
Lời giải:
Ta có a2(b + c) = b2(c + a).
⇔ a2b – ab2 + a2c – b2c = 0.
⇔ ab(a – b) + c(a2 – b2) = 0.
⇔ ab(a – b) + c(a – b)(a + b) = 0.
⇔ (a – b)(ab + ca + bc) = 0 (vì a ≠ b nên a – b ≠ 0).
⇔ ab + bc + ca = 0.
Lại có a2(b + c) = b2(c + a).
.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
(a ≠ b).
⇒ a2 = (a + b)(a + c).
⇒ a2(b + c) = (a + b)(a + c)(b + c).
⇒ 2012 = (a + b)(ab + ac + bc + c2).
⇒ 2012 = (a + b)c2.
Vậy M = c2(a + b) = 2012.
Câu 20: Phân tích số 20 ra thừa số nguyên tố.
Lời giải:
Ta có 20 = 22.5.
Vậy khi phân tích số 20 ra thừa số nguyên tố, ta được kết quả là 22.5.
Câu 21: Giải phương trình: (x2 + 2x)2 – 6x2 – 12x + 5 = 0.
Lời giải:
Ta có (x2 + 2x)2 – 6x2 – 12x + 5 = 0.
⇔ (x2 + 2x)2 – 6(x2 + 2x) + 5 = 0 (1)
Đặt t = x2 + 2x.
Phương trình (1) tương đương với: t2 – 6t + 5 = 0.
⇔ t = 5 hoặc t = 1.
Với t = 5, ta có: x2 + 2x – 5 = 0.
.
Với t = 1, ta có: x2 + 2x – 1 = 0.
.
Vậy tập nghiệm của phương trình đã cho là: .
Lời giải:
Giả sử mức lương cũ là 100%. Suy ra mức lương mới là 120% mức lương cũ.
Giả sử giá hàng cũ là 100%. Suy ra giá hàng mới là 80% giá hàng cũ.
Tỉ số phần trăm giữa lượng hàng mới và hàng cũ là:
Vậy lượng hàng mới sẽ mua được nhiều hơn lượng hàng cũ là: 150% – 100% = 50%.
Câu 23: Tìm số tự nhiên nhỏ nhất có bốn chữ số chia 5 dư 1 và chia 7 dư 1.
Lời giải:
Gọi số cần tìm là a (a ∈ ℕ), 1000 ≤ a ≤ 9999).
Gọi x là thương khi chia a cho 5; y là thương khi chia a cho 7.
Khi đó a – 1 = 5x và a – 1 = 7y.
Vì vậy a – 1 ∈ BC(5, 7).
Ta có BCNN(5, 7) = 35.
Suy ra BC(5, 7) = {0; 35; 70; 105; 140; ...; 980; 1015; 1050; 1085; ...}.
Vì a là số tự nhiên nhỏ nhất có 4 chữ số nên a – 1 = 1015.
Suy ra a = 1015 + 1 = 1016.
Vậy số cần tìm là 1016.
Câu 24: Cho x > y > 0 thỏa mãn 3x2 + 3y2 = 10xy. Tính giá trị của biểu thức .
Lời giải:
Ta có 3x2 + 3y2 = 10xy.
⇔ 3x2 – 10xy + 3y2 = 0.
⇔ 3x2 – 9xy – xy + 3y2 = 0.
⇔ 3x(x – 3y) – y(x – 3y) = 0.
⇔ (x – 3y)(3x – y) = 0.
⇔ x = 3y hoặc 3x = y.
So với điều kiện x > y > 0, ta nhận x = 3y.
Thế x = 3y vào P ta được: .
Vậy .
Lời giải:
Trục hoành: y = 0.
Suy ra giao điểm của parabol cần tìm và trục hoành là điểm A(–1; 0).
Ta có parabol đi qua điểm A(–1; 0).
Suy ra 0 = a – b + c (1)
Ta có parabol có đỉnh I(3; 4).
Suy ra
Do đó 6a + b = 0 (2)
Ta có parabol đi qua điểm I(3; 4).
Suy ra 4 = 9a + 3b + c (3)
Từ (1), (2), (3), ta có hệ phương trình: .
Vậy .
Câu 26: Tính tổng sau: 300 – (–200) – (–120) + 18.
Lời giải:
Ta có: 300 – (–200) – (–120) + 18.
= (300 + 200) + (120 + 18).
= 500 + 138.
= 638.
Câu 27: Cung lồi, cung lõm và điểm uốn là gì?
Lời giải:
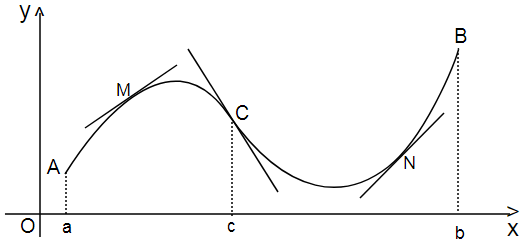
+ Cung lồi: Tại mọi điểm của cung AC, tiếp tuyến luôn nằm bên trên cung, khi đó ta nói cung AC là một cung lồi. Khoảng [a; c] ứng với cung lồi AC gọi là khoảng lồi của đồ thị (với a là hoành độ điểm A, c là hoành độ điểm C).
+ Cung lõm: Trên cung CB, mọi tiếp tuyến đều nằm dưới đồ thị, khi đó CB được gọi là cung lõm và đoạn [c; b] là khoảng lõm của đồ thị.
+ Điểm uốn: Điểm chuyển tiếp giữa cung lồi và cung lõm (từ lồi chuyển sang lõm hoặc từ lõm chuyển sang lồi) gọi là điểm uốn của đồ thị. Trong đồ thị trên, điểm C là điểm uốn.
Câu 28: Mẹ hơn con 30 tuổi, tuổi mẹ gấp 6 lần tuổi con. Hỏi tuổi của mỗi người?
Lời giải:
Tuổi mẹ là 6 phần, tuổi con là 1 phần.
Hiệu số phần bằng nhau là:
6 – 1 = 5 (phần).
Giá trị của một phần là:
30 : 5 = 6 (tuổi).
Tuổi con là:
6 × 1 = 6 (tuổi).
Tuổi mẹ là:
6 × 6 = 36 (tuổi).
Đáp số: Tuổi mẹ: 36 tuổi;
Tuổi con: 6 tuổi.
Câu 29: Cho hàm số y = f(x) = (5 – 3a)x + a + 6.
a) Với giá trị nào của a thì hàm số đồng biến, nghịch biến?
b) Biết f(–2) = 10. Tính f(2).
c) Biết f(3) = 5, hàm số đã cho đồng biến hay nghịch biến?
Lời giải:
a) Hàm số đã cho đồng biến ⇔ 5 – 3a > 0.
.
Hàm số đã cho nghịch biến ⇔ 5 – 3a < 0.
.
Vậy thì hàm số đã cho đồng biến; thì hàm số đã cho nghịch biến.
b) Ta có f(–2) = 10.
⇔ (5 – 3a).(–2) + a + 6 = 10.
⇔ –10 + 6a + a + 6 = 10.
⇔ 7a = 14.
⇔ a = 2.
Khi đó ta có hàm số y = f(x) = –x + 8.
Vậy f(2) = –2 + 8 = 6.
c) Với f(3) = 5, ta có: (5 – 3a).3 + a + 6 = 5.
⇔ 15 – 9a + a + 6 = 5.
⇔ 8a = 16.
⇔ a = 2.
Vì nên hàm số đã cho nghịch biến khi f(3) = 5.
Lời giải:
Chọn 2 chữ số lẻ từ 5 chữ số lẻ và có sắp xếp thứ tự thì có cách.
Chọn 3 chữ số chẵn từ 5 chữ số chẵn thì có cách.
Chọn 3 chữ số chẵn từ 5 chữ số chẵn, trong đó có mặt chữ số 0 thì có cách.
Coi 2 chữ số lẻ là 1 chữ số, kết hợp với 3 chữ số chẵn ta được 4 “chữ số”, sau đó sắp xếp thứ tự chúng thì có 4! cách.
Trường hợp chữ số 0 đứng đầu thì có 3! cách.
Vậy số các số thỏa mãn yêu cầu bài toán là: (số).
Lời giải:
Gọi là số tự nhiên có 4 chữ số khác nhau được lập từ các chữ số 0, 1, 3, 6, 9.
Ta có:
⦁ a có 4 cách chọn (a ≠ 0).
⦁ b có 4 cách chọn.
⦁ c có 3 cách chọn.
⦁ d có 2 cách chọn.
Suy ra ta có tất cả 4.4.3.2 = 96 số tự nhiên có 4 chữ số khác nhau.
Ta thấy các số có 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 3, 6, 9.
Gọi là số tự nhiên có 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 3, 6, 9.
Khi đó:
⦁ m có 3 cách chọn (m ≠ 0).
⦁ n có 3 cách chọn.
⦁ p có 2 cách chọn.
⦁ q có 1 cách chọn.
Suy ra ta có tất cả 3.3.2.1 = 18 số tự nhiên 4 chữ số khác nhau và chia hết cho 3 được lập từ các số 0, 1, 3, 6, 9.
Vậy ta có tất cả 96 – 18 = 78 số thỏa mãn yêu cầu bài toán.
Câu 32: Tính giá trị của biểu thức D = (3x + 5)(2x – 1) + (4x – 1)(3x + 2), với |x| = 2.
Lời giải:
Ta có D = (3x + 5)(2x – 1) + (4x – 1)(3x + 2)
= 6x2 – 3x + 10x – 5 + 12x2 + 8x – 3x – 2
= 18x2 + 12x – 7.
Theo đề, ta có
Thay x = 2 vào D, ta được: D = 18.22 + 12.2 – 7 = 89.
Thay x = –2 vào D, ta được: D = 18.(–2)2 + 12.(–2) – 7 = 41.
Vậy D = 89 hoặc D = 41 khi |x| = 2.
Lời giải:
Vì a, b, c không âm và a + b + c = 2 nên 0 ≤ a, b, c ≤ 2.
Khi đó ta có:
⦁ a ≤ 12a;
⦁ 2b2 = 2b.b ≤ 4b ≤ 12b;
⦁ 3c3 = 3c2.c ≤ 3.22.c = 12c.
Suy ra P = a + 2b2 + 3c3 ≤ 12(a + b + c) = 12.2 = 24.
Dấu “=” xảy ra .
Vậy Pmax = 24 khi (a; b; c) = (0; 0; 2).
Lời giải:
Số thứ ba là: 13,68 – 5,79 = 7,89.
Số thứ hai là: 12,45 – 7,89 = 4,56.
Số thứ nhất là: 5,79 – 4,56 = 1,23.
Đáp số: Số thứ nhất: 1,23;
Số thứ hai: 4,56;
Số thứ ba: 7,89.
Câu 35: Giải phương trình: x2 + x – 1 = 0.
Lời giải:
Ta có x2 + x – 1 = 0.
∆ = 12 – 4.1.(–1) = 5 > 0.
Do đó phương trình đã cho có 2 nghiệm phân biệt.
Hai nghiệm là:
Vậy tập nghiệm của phương trình đã cho là .
Câu 36: Tìm x, biết: x : 0,25 + x × 11 = 24.
Lời giải:
Ta có x : 0,25 + x × 11 = 24
x × 4 + x × 11 = 24
x × (4 + 11) = 24
x × 15 = 24
x = 24 : 15
x = 1,6
Vậy x = 1,6.
A. 42,85%.
B. 30%.
C. 70%.
D. 233,33%.
Lời giải:
Đáp án đúng là: B
Trong vườn có tổng số cây là:
12 + 28 = 40 (cây)
Tỉ số phần trăm của cây cam so với tổng số cây trong vườn là:
12 : 40 = 0,3 = 30%
Đáp số: 30%.
Câu 38: Hãy so sánh: 2565 và 318.
Lời giải:
Ta có 2565 = (28)5 =28.5 = (25)8 = 328.
Vì 31 < 32 nên 318 < 328.
Vậy 318 < 2565.
Lời giải:
Vì (d) // (d1) nên phương trình đường thẳng (d) có dạng: y = –2x + b (b ≠ 5).
Ta có (d) đi qua điểm A(–2; 1). Suy ra 1 = –2.(–2) + b.
Khi đó b = –3 (nhận).
Vậy phương trình (d): y = –2x – 3.
Lời giải:
Ta có
Vậy ta có điều phải chứng minh.