Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 21)

Câu 1: Cho tam giác ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh:

a) Tứ giác ABCD là hình bình hành.

b) Tứ giác ABCD là hình thoi.

Lời giải:

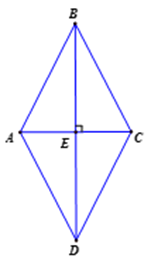
a) Vì △ABC cân tại B có đường cao BE Þ BE là đường trung tuyến

Þ EA = EC (1)

Ta có: EB = ED (gt) (2)

Từ (1) và (2) suy ra ABCD là hình bình hành.

b) Vì BE là đường cao của △ABC => BE ^ AC

Hình bình hành ABCD có BE ^ AC => ABCD là hình thoi.

Câu 2: Cho đồ thị (d): y = (3m − 2)x + m − 2 với m là tham số

a) Tìm điểm cố định mà d luôn đi qua mọi giá trị của m

b) Tìm m để khoảng cách từ gốc tọa độ đến d lớn nhất

Lời giải:

a) Gọi M(x; y) là điểm cố định mà (d) luôn đi qua

Ta có M(x; y) thuộc (d) nên

y = (3m − 2)x + m − 2

<=> 3mx − 2x + m − 2 − y = 0

<=> m(3x + 1) − (2x + y + 2) = 0

$$\begin{gathered} \iff \left\{\begin{array}{l}3x+1=0\\ 2x+y+2=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-\frac{1}{3}\\ y=-\frac{4}{3}\end{array}\right. \end{gathered}$$

Vậy $M\left(\frac{-1}{3};\frac{2}{3}\right)$  là điểm cố định mà (d) luôn đi qua với mọi giá trị của m.

b) (d): y = (3m − 2)x + m − 2

Û (3m − 2)x − y + m − 2 = 0

Khoảng cách từ gốc tọa độ đến d là:

$d=\frac{\left|m-2\right|}{\sqrt{{\left(3m-2\right)}^2+{\left(-1\right)}^2}}=\frac{\left|m-2\right|}{\sqrt{9m^2-12m+5}}$

Vậy để d lớn nhất thì m = 1 và khi đó $d=\frac{1}{\sqrt{2}}$

Câu 3: Tính nhanh $\frac{x^2-6xy+9y^2}{3y-x}$ .

Lời giải:

$$\begin{gathered} \frac{x^2-6xy+9y^2}{3y-x}=\frac{{\left(x-3y\right)}^2}{3y-x} \\ =\frac{{\left(3y-x\right)}^2}{3y-x}=3y-x \end{gathered}$$

Câu 4: Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 8.

b) Tích số chấm hai mặt xuất hiện là số lẻ.

Lời giải:

Vì một con xúc xắc có 6 mặt và khi gieo hai lần thì số phần tử của không gian mẫu là$\left|\Omega \right|=\left|6.6\right|=36$;

Gọi A là biến cố để tổng số chấm hai mặt xuất hiện bằng 8;

Các kết quả của biến cố A là: A = {(2;6),(3;5),(4;4),(5;3),(6;2)}

Số các kết quả của biến cố A là: 5;

Xác suất để tổng số chấm hai mặt xuất hiện bằng 8 là: $P\left(A\right)=\frac{5}{36}$ ;

b) Gọi B là biến cố: “Tích số chấm hai mặt xuất hiện là số lẻ ”

Tích số chấm hai mặt xuất hiện là số lẻ khi ở cả hai lần gieo đểu xuất hiện số lẻ nên có 3.3 = 9 cách gieo

Xác suất của tích số chấm hai mặt xuất hiện số lẻ là: $P\left(B\right)=\frac{9}{36}=\frac{1}{4}$ .

Câu 5: Gieo một con xúc xắc cân đối đồng chất 2 lần, tính xác suất để biến cố có tích 2 lần số chấm khi gieo xúc xắc là một số chẵn.

A. 0,25;

B. 0,5;

C. 0,75;

D. 0,85.

Lời giải:

Vì một con xúc xắc có 6 mặt và khi gieo hai lần thì số phần tử của không gian mẫu là $\left|\Omega \right|=\left|6.6\right|=36$.

Gọi A là biến cố để tích hai lần số chấm khi gieo xúc xắc là một số chẵn.

Trường hợp 1: 

Ở lần gieo thứ nhất số chấm xuất hiện trên mặt là số lẻ thì trong lần gieo thứ 2 số chấm xuất hiện phải là số chẵn nên có 3 . 3 = 9 (cách gieo).

Trường hợp 2:

Lần gieo thứ nhất số chấm xuất hiện trên mặt là số chẵn thì có hai trường hợp xảy ra là số chấm xuất hiện trên mặt khi gieo lần hai là số lẻ  hoặc số chẵn.

 Khi đó có 3 . 3 + 3 . 3 = 18 (cách gieo).

Suy ra số kết quả thuận lợi cho biến cố A là: $\left|\Omega \right|=9+18=27$

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{27}{36}=\mathrm{0,75}$ .

Đáp án đúng là: C.

Câu 6: Giải bất phương trình sau: 3x² – 4x + 4 > 0.

Lời giải:

Xét hàm số f(x) = 3x² – x + 4 vô nghiệm ∀ x ∈ ℝ .

Hệ số a của tam thức f(x): 3 > 0;

Suy ra, f(x) > 0 ∀ x ∈ ℝ

Vậy tập nghiệm của bất phương trình: S = ℝ.

Câu 7: Giải bất phương trình sau: – 3x² + x + 4 ≥ 0.

Lời giải:

Xét hàm số f(x) = –3x² + x + 4 có nghiệm x₁ = – 1; $x_2=\frac{4}{3}$ .

Hệ số a của tam thức f(x): – 3 < 0.

Suy ra, f(x) ≥ 0 $\iff -1\le x\le \frac{4}{3}$ .

Vậy tập nghiệm của bất phương trình: $S=\left[-1;\frac{4}{3}\right]$ .

Câu 8: Cho hàm số y = f(x) = ax².

a) Xác định a biết rằng khi x = 2 thì y = – 2.

b) Vẽ đồ thị (P) của hàm số với a tìm được.

Lời giải:

a) Ta có: x = 2 thì y = – 2

⇒ f(2) = – 2

⇒ a.2²  = – 2

⇔ 4a = – 2

$\iff a=\frac{-2}{4}=\frac{-1}{2}$

Vậy hàm số $y=-\frac{1}{2}{x}^2$ .

b) Hàm số $y=-\frac{1}{2}{x}^2$

Bảng giá trị:

x	– 2	– 1	0	1	2
y	– 2	$-\frac{1}{2}$	0	$\frac{1}{2}$	–2

Đồ thị (P) của hàm số

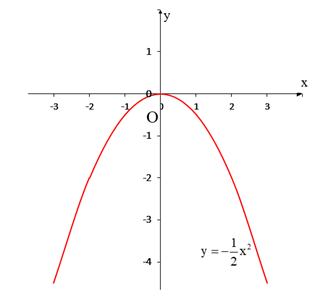
Câu 9: Cho hàm số y = f(x) = ax² – 2.

a) Hãy xác định a biết f(3) =16;

b) Tính f(2), f(– 2), f(0), f(1), f(– 1).

Lời giải:

a) Ta có: f(3) = 16

⇒ a.3² – 2 = 16 ⇔ 9a = 18

⇔ a = 2

Vậy hàm số y = f(x) = 2x² – 2 

b) Ta có f(x) = 2x² – 2 ;

f(2) = 2.2² – 2 = 8 – 2 = 6;

f(– 2) = 2.( –2)² – 2 = 8 – 2 = 6;

f(1) = 2.1² – 2 = 2 – 2 = 0;

f(0) = 2.0² – 2 = 0 – 2 = – 2;

f(–1) = 2.( –1)² – 2 = 2 – 2 = 0.

Câu 10: Tìm x, biết: x + 456,95 × 8 = 5248.

Lời giải:

Ta có:

x + 456,95 × 8 = 5248

x + 3655.6 = 5248

x = 5248 – 3655,6

x = 1529,4

Vậy x = 1529,4.

Câu 11: Phân tích đa thức thành nhân tử: 2x² – 3x – 2.

Lời giải:

2x² – 3x – 2

= 2x² – 4x + x – 2

= (2x² – 4x) + (x – 2)

= 2x(x – 2) + (x – 2)

= (2x + 1)(x – 2).

Câu 12: Giải phương trình: $\sqrt{3}\sin x+\cos x=1$.

Lời giải:

$\begin{array}{l}\sqrt{3}\sin x+\cos x=1\\ \iff \frac{\sqrt{3}}{2}\sin x+\frac{1}{2}\cos x=\frac{1}{2}\\ \iff \sin x.\cos \frac{\pi }{6}+\cos x.\sin \frac{\pi }{6}=\frac{1}{2}\\ \iff \sin \left(x+\frac{\pi }{6}\right)=\frac{1}{2}\\ \iff \left[\begin{array}{l}x+\frac{\pi }{6}=\frac{\pi }{6}+k2\pi \\ x+\frac{\pi }{6}=\frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\\ \iff \left[\begin{array}{l}x=k2\pi \\ x=\frac{2\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$.

Câu 13: Nghiệm của phương trình: $\sqrt{3}\sin x-\cos x=2$ là:

A. $x=\frac{2\pi }{3}+k2\pi$.

B. $x=\frac{\pi }{6}+k2\pi$.

C. $x=\frac{\pi }{3}+k2\pi$.

D. $x=\frac{5\pi }{6}+k2\pi$.

Lời giải:

Đáp án đúng là: A

$\begin{array}{l}\sqrt{3}\sin x-\cos x=2\\ \iff \frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=1\\ \iff \sin x.\cos \frac{\pi }{6}-\cos x.\sin \frac{\pi }{6}=1\\ \iff \sin \left(x-\frac{\pi }{6}\right)=1\\ \iff x-\frac{\pi }{6}=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)\\ \iff x=\frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)\end{array}$

Câu 14: Một vật hình hộp chữ nhật có kích thước (30×20×10 cm).

a) Tính thể tích của vật.

b) Tính lực đẩy Ác – si – mét tác dụng lên vật khi thả đứng nó vào trong chất lỏng có trọng lượng riêng 12000 N/m³. Biết khi đó chiều cao của vật bị chìm trong chất lỏng là 20 cm.

Lời giải:

a) Thể tích vật là:

V = abc = 30.20.10 = 6000 cm³ = 6.10^–3 m³

b) Thể tích chìm trong chất lỏng là:

V’ = 20.20.10 = 4000 cm³ = 4.10^–3 m³

Lực đẩy Ác – si – mét là:

F_A = dV’ = 12000.4.10^–3 = 48 N.

Câu 15: Hai tổ cùng làm một công việc nếu làm chúng thì hoàn thành trong 15 giờ. Nếu tổ 1 làm trong 5 giờ, tổ 2 làm trong 3 giờ thì đuợc 30% công việc. Hỏi nếu làm 1 mình thì mỗi tổ làm trong bao lâu ?

Lời giải:

Gọi số ngày tổ 1 làm một mình hết công việc là: x (giờ); số ngày tổ 2 làm một mình hết công việc là: y (giờ)

(x, y > 0)

Một ngày một mình tổ 1 làm được: $\frac{1}{x}$ (công việc)

Một ngày một mình tổ 2 làm được: $\frac{1}{y}$ (công việc)

Vì cả hai tổ làm chung thì 15 giờ xong nên ta có phương trình:

$15.\left(\frac{1}{x}+\frac{1}{y}\right)=1\Rightarrow \frac{15}{x}+\frac{15}{y}=1$ (công việc)

Vì tổ 1 làm trong 5 giờ, tổ 2 làm trong 3 giờ thì làm được 30% công việc nên ta có phương trình:

$\frac{5}{x}+\frac{3}{y}=\frac{3}{10}$ (công việc)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}\frac{15}{x}+\frac{15}{y}=1\\ \frac{5}{x}+\frac{3}{y}=\frac{3}{10}\end{array}\right.\Rightarrow \left\{\begin{array}{l}x=20\\ y=60\end{array}\right.$

Vậy đội 1 làm một mình thì sau 20 giờ sẽ xong việc; đội 2 làm một mình thì sau 60 giờ sẽ xong công việc.

Câu 16: Với giá trị nào của a và b thì đa thức x³ + ax² + 2x + b chia hết cho đa thức x² + x + 1.

Lời giải:

$\begin{array}{l}{x}^3+a{x}^2+2x+b=x\left(x^2+x+1\right)+\left(a-1\right)\left(x^2+x+1\right)+x+b-\left(a-1\right)x-\left(a-1\right)\\ =\left(x+a-1\right)\left(x^2+x+1\right)+x\left(2-a\right)+\left(b-a+1\right)\end{array}$

Thấy rằng bậc của x(2 – a) + (b – a + 1) nhỏ hơn bậc của x²  + x + 1 nên nó là số dư của x³ + ax² + 2x + b chia cho x² + x + 1

Như vậy để thỏa mãn yêu cầu để bài thì: x(2 – a) + (b – a + 1) = 0

Hay a = 2; b = 1

Vây (a; b) = (2; 1).

Câu 17: Tìm x để $\sqrt{2x-1}$ có nghĩa ?

Lời giải:

$\sqrt{2x-1}$ có nghĩa $\iff 2x-1\ge 0\iff x\ge \frac{1}{2}$.

Câu 18: Cho tam giác OAB vuông tại A, OA = 3 cm, AB = 4 cm, đường cao AH (H thuộc OB)

a) Tính AH.

b) Vẽ đường tròn (O; OA) cắt tia AH tại C. Chứng minh: CB là tiếp tuyến của đường tròn (O; OA).

Lời giải:

a)

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH ta có:

$\frac{1}{A{H}^2}=\frac{1}{O{A}^2}+\frac{1}{A{B}^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\Rightarrow A{H}^2=\frac{144}{25}\Rightarrow AH=\frac{12}{5}=\mathrm{2,4}$ (cm)

b)

 

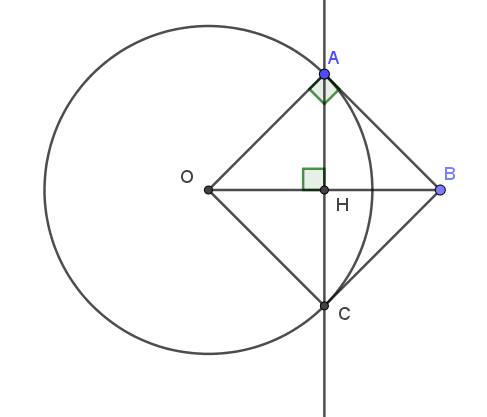
Xét đường tròn O có: OH là một phần đường kính, AC là dây cung, OH vuông góc với AC tại H nên H là trung điểm của AC

Do đó, OB là đường trung trực của AC nên ta có: AB = CB

Xét tam giác OAB và tam giác OCB có:

AB = CB 

OB chung

OA = OB (cùng bằng bán kính)

Do đó, tam giác OAB bằng tam giác OCB

Do đó, ta có: $\widehat{OCB}=\widehat{OAB}=90°$ 

Vậy BC vuông góc với bán kính OC nên BC  là tiếp tuyến của đường tròn tâm O

Câu 19: Giải phương trình với ẩn số nguyên dương n thỏa mãn:

$A_n^2-3C_n^2=15-5n$.

A. n = 5 hoặc n = 6.

B. n = 5 hoặc n = 6 hoặc n = 12.

C. n = 6.

D. n = 5.

Lời giải:

Đáp án đúng là: A

Ta có:

$A_n^2-3C_n^2=15-5n$

$$\begin{gathered} \begin{array}{l}\iff \frac{n!}{\left(n-2\right)!}-3.\frac{n!}{\left(n-2\right)!.2!}=15-5n\\ \iff n\left(n-1\right)-\frac{3}{2}.n\left(n-1\right)=15-5n\end{array} \\ \iff n^2-n-\frac{3}{2}{n}^2+\frac{3}{2}n=15-5n \\ \begin{array}{l}\iff -\frac{1}{2}{n}^2+\frac{11}{2}n-15=0\\ \iff \left[\begin{array}{l}n=6\\ n=5\end{array}\right.\end{array} \end{gathered}$$

Câu 20: Có bao nhiêu cách xếp 5 nam và 5 nữ thành hàng dọc sao cho 5 nam đứng liền nhau ?

A. 3628800.         

B. 86400.              

C. 14400.              

D. 28800.

Lời giải:

Đáp án đúng là: B

Coi 5 nam là một nhóm, số cách xếp nhóm 5 bạn vào một hàng dọc 10 chỗ là: 6 cách.

Số cách hoán vị chỗ của 5 nam trong nhóm là: 5!.

Số cách hoán vị chỗ của 5 nữ cho 5 vị trí còn lại là: 5!

Vậy số cách xếp thỏa mãn yêu cầu đề bài là: 6.5!.5! = 86400.

Câu 21: Có bao nhiêu số tự nhiên lớn hơn 4000 có 4 chữ số được lập từ các số 1, 2, 5, 7 nếu:

a) Các chữ số của số đó không nhất thiết phải khác nhau.

b) Các chữ số của số đó khác nhau.

Lời giải:

Gọi số cần tìm là $\overline{abcd}$ ở đó a, b, c, d thuộc {1; 2; 5; 7}

a)

Để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng chữ số 5 hoặc 7.

Vậy chữ số a có 2 cách chọn, chữ số b có 4 cách chọn, chữ số c có 4 cách chọn, d cũng có 4 cách chọn.

Suy ra có tất cả các chữ số lớn hơn 4000 là 2.4.4.4 = 128 (số)

b)

Để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng 5 hoặc 7

mà các chữ số khác nhau suy ra b có 3 cách chọn, c có 2 cách chọn và d có 1 cách chọn

Số các chữ số cần tìm là: 2.3.2.1=12 số.

Câu 22: Tính hàm số lượng giác: $\frac{1}{1+{\tan }^{2}x}+\frac{1}{1+{\cot }^{2}x}$.

Lời giải:

$\begin{array}{l}\frac{1}{1+{\tan }^{2}x}+\frac{1}{1+{\cot }^{2}x}\\ =\frac{1}{\frac{1}{co{s}^{2}x}}+\frac{1}{\frac{1}{{\sin }^{2}x}}=co{s}^{2}x+{\sin }^{2}x=1\end{array}$

Câu 23: Cho hình thang ABCD có hai đường chéo AC cắt BD tại O. Tính diện tích hình thang ABCD, biết diện tích tam giác AOB là 6 cm², diện tích tam giác AOD là 10 cm².

Lời giải:

AB song song với CD

$$\begin{gathered} \Rightarrow S_{BAD}=S_{ABC}\Rightarrow S_{BAD}-S_{OAB}=S_{ABC}-S_{OAB}\Rightarrow S_{OAD}=S_{OBC}=10c{m}^2 \\ \frac{OB}{OD}=\frac{S_{OAB\text{}}}{S_{OAD}}=\frac{6}{10}=\frac{3}{5} \\ \frac{S_{OBC}}{S_{ODC}}=\frac{OB}{OD}=\frac{3}{5} \\ \Rightarrow S_{ODC}=\frac{5}{3}{S}_{OBC}=\frac{5}{3}.10=\frac{50}{3}\left(c{m}^2\right) \\ {S}_{ABCD}=S_{OAB}+S_{OAD}+S_{OBC}+S_{ODC}=6+10+10+\frac{50}{3}=\frac{128}{3}\left(c{m}^2\right) \end{gathered}$$

Câu 24: Phân tích ${\sin }^{8}x+co{s}^{8}x$.

Lời giải:

$\begin{array}{l}{\sin }^{8}x+co{s}^{8}x\\ ={\left({\sin }^{4}x+co{s}^{4}x\right)}^2-2{\sin }^{4}x.co{s}^{4}x\\ ={\left(1-2{\sin }^{2}x.co{s}^{2}x\right)}^2-\frac{1}{8}{\sin }^{4}2x\\ ={\left(1-\frac{1}{2}{\sin }^{2}2x\right)}^2-\frac{1}{8}{\sin }^{4}2x\\ =1-{\sin }^{2}2x+\frac{1}{8}{\sin }^{4}2x\end{array}$

$\begin{array}{l}=1-\frac{1-cos4x}{2}+\frac{1}{8}{\left(\frac{1-cos4x}{2}\right)}^2\\ =1-\frac{1-cos4x}{2}+\frac{1}{32}\left(1-2cos4x+\frac{1+\cos 8x}{2}\right)\\ =\frac{35}{64}+\frac{7}{16}cos4x+\frac{1}{64}cos8x\end{array}$

Câu 25: Giải phương trình sau: ${\sin }^{8}x+co{s}^{8}x=\frac{1}{8}$.

Lời giải:

Ta có:

$\begin{array}{l}{\sin }^{2}x+co{s}^{2}x=1\\ \Rightarrow {\sin }^{4}x+co{s}^{4}x={\left({\sin }^{2}x+{\cos }^{2}x\right)}^2-2{\sin }^{2}x.co{s}^{2}x\\ =1-2{\sin }^{2}x.co{s}^{2}x\\ \Rightarrow {\sin }^{8}x+co{s}^{8}x={\left({\sin }^{4}x+co{s}^{4}x\right)}^2-2{\sin }^{4}x.co{s}^{4}x\\ =1+{\sin }^{4}x.co{s}^{4}x-4{\sin }^{2}x.co{s}^{2}x\\ =1+2{\sin }^{2}x.co{s}^{2}x.\left({\sin }^{2}x.co{s}^{2}x-2\right)\\ =1+\frac{{\sin }^{2}2x}{2}.\left(\frac{{\sin }^{2}2x}{4}-1\right)\end{array}$

Đặt t = sin²2x (0 < t < 1)

Phương trình đã cho có dạng:

$\begin{array}{l}1+\frac{t}{2}\left(\frac{t}{4}-2\right)=\frac{1}{8}\\ \iff 8+t^2-8t=1\\ \iff t^2-8t+7=0\\ \Rightarrow \left(t-1\right)\left(t-7\right)=0\\ \iff t=1\left(TM\right)\end{array}$

Với t = 1 ta có:

${\sin }^{2}2x=1\Rightarrow \left\{\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=-\frac{\pi }{4}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$.

Câu 26: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có: $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$.

Lời giải:

Do ABCD là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}$

$\begin{array}{l}\Rightarrow \overrightarrow{AM}+\overrightarrow{MB}=\overrightarrow{DM}+\overrightarrow{MC}\\ \Rightarrow -\overrightarrow{MA}+\overrightarrow{MB}=-\overrightarrow{MD}+\overrightarrow{MC}\\ \Rightarrow \overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\end{array}$

Câu 27: Nếu tam giác ABC có 3 góc thỏa mãn sinA = cosB + cosC thì tam giác ABC là tam giác gì ?

Lời giải:

 

$$\begin{gathered} \sin A=\cos B+\cos C=2cos\frac{B+C}{2}.cos\frac{B-C}{2} \\ =2\sin \frac{A}{2}.cos\frac{B-C}{2} \\ \iff 2\sin \frac{A}{2}.cos\frac{A}{2}=2\sin \frac{A}{2}.cos\frac{B-C}{2} \\ \iff cos\frac{A}{2}=cos\frac{B-C}{2}\Rightarrow \frac{A}{2}=\frac{B-C}{2} \\ \begin{array}{l}\Rightarrow \widehat{B}=\widehat{A}+\widehat{C}\\ \Rightarrow 2\widehat{B}=180°\Rightarrow \widehat{B}=90°\end{array} \end{gathered}$$

Câu 28: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân Các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

Lời giải:

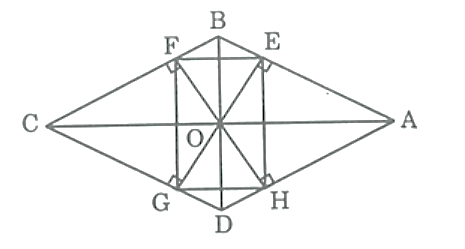
Ta có:

AB song song với CD (gt)

OE vuông góc với AB (gt)

Do đó, OE vuông góc với CD

OG  vuông góc với CD (gt)

Suy ra OE trùng với OG nên ba điểm O, E, G thẳng hàng

BC song song với AD (gt)

OF vuông góc với BC (gt)

Do đó, OF vuông góc với AD

Suy ra, OF trùng với OH nên ba điểm O, H, F thẳng hàng

Vì AC và BD là đường phân giác các góc của hình thoi nên:

OE = OF (tính chất tia phân giác) (1)

OE = OH (tính chất tia phân giác) (2)

OH = OG (tính chất tia phân giác) (3)

Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.

Câu 29: Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau tại K.

a) Tứ giác OBKC là hình gì ? Vì sao ?

b) Chứng minh rằng AB = OK.

c) Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông. 

Lời giải:

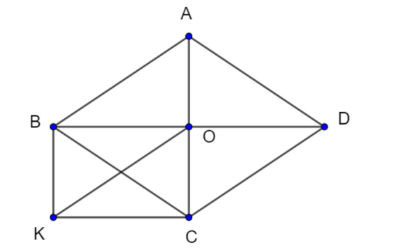
a)

Ta có tứ giác ABCD là hình thoi

Do đó, AC vuông góc với BD (tính chất 2 đường chéo trong hình thoi)

Ta có: BK song song với OC, KC song song với OB

Do đó, Tứ giác BOCK là hình bình hành

Mà $\widehat{BOC}=90°$

Do đó, BOCK là hình chữ nhật

b)

ABCD là hình thoi nên AB = BC = CD = DA (3)

Do OBIC là hình chữ nhật nên 2 đường chéo OI = BC (4)

Từ (3) và (4) suy ra AB = OI

c)

Để OBKC là hình vuông thì OB = OC

Do đó, ABCD phải là hình vuông.

Câu 30: Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng tổng của 31 số đo là số dương.

Lời giải:

Trong 31 số đã cho có ít nhất 1 số là số dương (vì nếu 31 số đã cho đều âm thì tổng của 5 số bất kỳ không thể là 1 số dương)

Tách riêng số dương đó ra còn 30 số, nhóm 5 số vào 1 nhóm thì được 6 nhóm. Trong đó nhóm nào cũng là 1 số dương

Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách.

Vậy tổng của 31 số đó là 1 số dương.

Câu 31: Cho các hàm số y = x + 1 có đồ thị là d₁ và y = – x + 3 có đồ thị là d₂.

a) Vẽ đồ thị hai hàm số trên trên cùng một mặt phẳng tọa độ.

b) Gọi A, B lần lượt là giao điểm của d_1­, d₂ với trục hoành và C là giao điểm của d₁ và d₂. Hãy tìm tọa độ các điểm A, B và C.

Lời giải:

a)

Đồ thị hàm số y = x + 1 là đường thẳng d₁ đi qua hai điểm (–1; 0) và (0; 1)

Đồ thị hàm số y = –x + 3 là đường thẳng d₂ đi qua hai điểm (3; 0) và (0; 3)

Vẽ hai đường thẳng d₁ và d₂ trên mặt phẳng Oxy như hình vẽ:

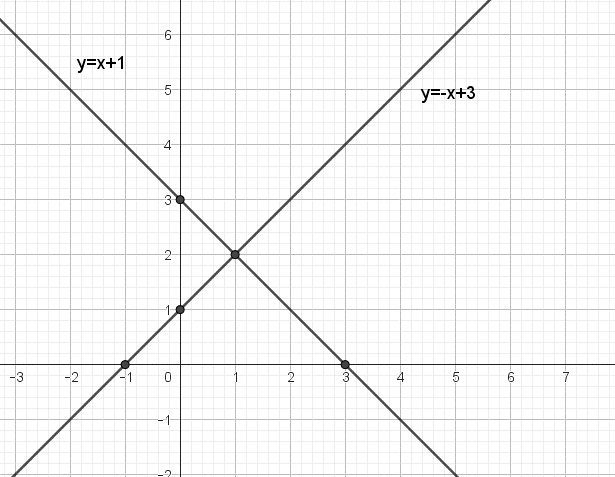
b)

Gọi A(x­_A; y_A), B(x_B; y_B) lần lượt là giao điểm của d_1­, d₂ với trục hoành và C(x_C; y_C) là giao điểm của d₁ và d₂.

Ta có:

y_A­ = 0 ⇒ x_A + 1 = 0 ⇒ x_A = –1 ⇒ A(–1; 0)

y_B = 0 ⇒ –x_B + 3 = 0 ⇒ x_B = 3 ⇒ B(3; 0)

x_C là nghiệm của phương trình hoành độ giao điểm:

x + 1 = –x + 3

⇔ 2x = 2

⇔ x = 1

Do đó, x_C = 1 , y_C = 2 ⇒ C(1; 2).

Câu 32: Một hình chữ nhật có chu vi là 96 cm, chiều rộng bằng $\frac{3}{5}$ chiều dài. Tính diện tích của hình chữ nhật đó.

Lời giải:

Nửa chu vi hình chữ nhật đó là:

96 : 2 = 48 (cm)

Tổng số phần bằng nhau là:

3 + 5 = 8 (phần)

Chiều dài hình chữ nhật là:

48 : 8 x 5 = 30 (cm)

Chiều rộng hình chữ nhật là:

48 : 8 x 3 = 18 (cm)

Diện tích hình chữ nhật là:

18 x 30 = 540 (cm²).

Câu 33: Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác ?

A. 6.

B. 8.

C. 10.

D. 12.

Lời giải:

Đáp án đúng là: D

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt.

Từ 4 điểm ban đầu ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối.

Do đó; có tất cả 4.3 = 12 vecto được tạo ra.

Câu 34: Tính căn bậc 2 của số thực n trong C.

Lời giải:

#include

#include

int main()

{

    int a = 13; //Gắn giá trị cần khai căn, hoặc có thể cho nhập từ bàn phím

    float cb2 = (float)sqrt(a);//Tính căn bậc 2 của a

    printf("can ba 2 cua so %d la: %f",a, cb2); //Hiển thị kết quả

}

Câu 35: Cho tam giác ABC, AH vuông góc với BC, AH = 12cm, AB = 15cm, CH = 16cm.

a) Tính độ dài BH, AC.

b) Tam giác ABC có phải là tam giác vuông không? Vì sao?

Lời giải:

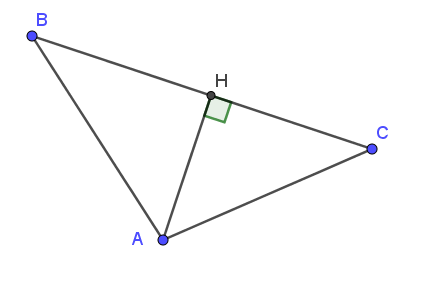
a)

Xét tam giác AHB vuông tại H

Áp dụng định lí Py–ta–go ta có:

AH² + BH² = AB²

$\Rightarrow BH=\sqrt{A{B}^2-A{H}^2}=\sqrt{{15}^2-{12}^2}=9$ (cm)

Xét tam giác AHC vuông tại H

Áp dụng định lí Py–ta–go ta có:

AH² + CH² = AC²

$\Rightarrow AC=\sqrt{C{H}^2+A{H}^2}=\sqrt{{16}^2+{12}^2}=20$ (cm)

b)

Xét tam giác ABC có:

BC = BH + CH = 9 + 16 = 25 (cm)

$A{B}^2+A{C}^2={15}^2+{20}^2=625={25}^2=B{C}^2$

Do đó, theo định lý Py–ta–go đảo thì tam giác ABC vuông tại A.

Câu 36: Cho tam giác ABC, vẽ AH vuông góc vs BC (H thuộc BC), trên tia AH lấy D sao cho AH = HD. Chứng minh:

a) Tam giác ABH bằng tam giác DBH.

b) AC = CD.

c) Qua A kẻ đg thẳng song song vs BD cắt BC tại E. Chứng minh H là trung điểm của BE.

Lời giải:

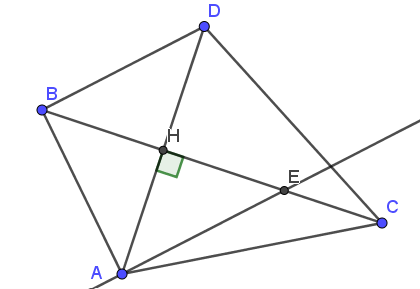
a)

Xét ΔBHA vuông tại H và ΔBHD vuông tại H có

BH chung

HA = HD

Do đó, tam giác BHA bằng tam giác BHD

b)

Xét tam giác CAD có

CH là đường cao

CH là đường trung tuyến

Do đó: ΔCAD cân tại C

hay CA = CD

c)

Xét ΔAHE vuông tại H và ΔDHB vuông tại H có

HA = HD

$\widehat{HAE}=\widehat{HDB}$

Do đó, tam giác AHE bằng tam giác DHB

Suy ra: HE = HB

Hay H là trung điểm của BE.

Câu 37: Tính nhanh: $\left(1-\frac{1}{4}\right)\times \left(1-\frac{1}{5}\right)\times \left(1-\frac{1}{6}\right)\times \left(1-\frac{1}{7}\right)\times \left(1-\frac{1}{8}\right)$.

Lời giải:

$\left(1-\frac{1}{4}\right)\times \left(1-\frac{1}{5}\right)\times \left(1-\frac{1}{6}\right)\times \left(1-\frac{1}{7}\right)\times \left(1-\frac{1}{8}\right)$

$=\frac{3}{4}\times \frac{4}{5}\times \frac{5}{6}\times \frac{6}{7}\times \frac{7}{8}$

$=\frac{3\times 4\times 5\times 6\times 7}{4\times 5\times 6\times 7\times 8}=\frac{3}{8}$.

Câu 38: Cho hai khoảng A = (m; m + 1) và B = (3; 5). Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.

Lời giải:

A ∪ B là một khoảng khi A ∩ B = Ø

Khi đó:

5 ≤ m hoặc m + 1 ≤ 3 ⇔ m ≤ 2 hoặc m ≥ 5

Do đó: A ∪ B  là một khoảng ⇔ 2 < m < 5

Khi đó: Nếu 2 < m ≤ 3 thì A ∪ B  = (m; 5)

Nếu 3 < m ≤ 4 thì A ∪ B  = (3; 5)

Nếu 4 < m ≤ 5 thì A ∪ B  = (3; m + 1).

Câu 39: Tính tổng: S₁ = 1 + 2 + 3 + ... + 999.

Lời giải:

Số các số hạng của S1 là: (999 – 1) : 1 + 1 = 999 ( số hạng )

Tổng S₁ = (999 + 1) × 999 : 2 = 499500.

Câu 40: Tìm tập xác định của hàm số: $y=\frac{cos2x}{\tan x-1}$.

Lời giải:

Điều kiện xác định của hàm số là:

$\left\{\begin{array}{l}\cos x\ne 0\\ \tan x\ne -1\end{array}\right.\iff \left\{\begin{array}{l}x\ne -\frac{\pi }{4}+k\pi \\ x\ne \frac{\pi }{2}+k\pi \end{array}\right.$

Do đó, $D=ℝ\backslash \left\{-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right\}$.

Câu 41: Một hình chữ nhật có cạnh này bằng $\frac{2}{3}$ cạnh kia. Nếu bớt đi mỗi cạnh 5m thì diện tích hình chữ nhật đó giảm đi 16%. Tính kích thước của hình chữ nhật đó ?

Lời giải:

Gọi chiều dài hình chữ nhật là x (m, x > 5)

Suy ra chiều rộng hình chữ nhật là $\frac{2}{3}x$ (m)

Diện tích hình chữ nhật ban đầu là: $\frac{2}{3}{x}^2$ (m²)

Nếu bớt đi mỗi cạnh 5m thì diện tích giảm đi 16% nên ta có phương trình:

$\begin{array}{l}\left(x-5\right)\left(\frac{2}{3}x-5\right)=\frac{2}{3}{x}^2-16\%.\frac{2}{3}{x}^2\\ \iff -5x-\frac{10}{3}x+25=-16\%.\frac{2}{3}{x}^2\\ \iff \frac{8}{75}{x}^2-\frac{25}{3}x+25=0\\ \iff \left[\begin{array}{l}x=\frac{25}{8}\left(KTM\right)\\ x=75\left(TM\right)\end{array}\right.\end{array}$

Vậy diện tích hình chữ nhật là: $75.\frac{2}{3}.75=3750$ (m²).

Câu 42: Tìm m để $-9<\frac{3x^2+mx-6}{x^2-x+1}<6$ nghiệm đúng với mọi x ∈ ℝ.

Lời giải:

Bất phương trình đã cho tương ứng với:

$-9\left(x^2-x+1\right)<3x^2+mx-6<6\left(x^2-x+1\right)$

$\iff \left\{\begin{array}{l}12x^2+\left(m-9\right)x+3>0\left(1\right)\\ 3x^2-\left(m+6\right)x+12>0\left(2\right)\end{array}\right.$

Yêu cầu đề bài tương đương với (1) và (2) nghiệm đúng với mọi x thuộc ℝ

$\iff \left\{\begin{array}{l}\Delta \left(1\right)<0\\ \Delta \left(2\right)<0\end{array}\right.\iff \left\{\begin{array}{l}{\left(m-9\right)}^2-144<0\\ {\left(m+6\right)}^2-144<0\end{array}\right.\iff -3<m<6$.

Câu 43: Cho hệ phương trình: $\left\{\begin{array}{l}9x^2-16y^2=144\\ x-y=m\end{array}\right.$. Tìm m để hệ có nghiệm duy nhất.

Lời giải:

$\begin{array}{l}\left\{\begin{array}{l}9x^2-16y^2=144\\ x-y=m\end{array}\right.\iff \left\{\begin{array}{l}9{\left(m+y\right)}^2-16y^2=144\\ x=m+y\end{array}\right.\\ \iff \left\{\begin{array}{l}9y^2+18my+9m^2-16y^2=144\\ x=m+y\end{array}\right.\iff \left\{\begin{array}{l}-7y^2+18my-144=0\left(1\right)\\ x=m+y\end{array}\right.\end{array}$
Để (1) có 1 nghiệm duy nhất thì $\Delta \text{'}=0\iff 9m^2-(-7).(-144)=0\iff m=4\sqrt{7}$

Câu 44: Tìm a, b để hệ phương trình $\left\{\begin{array}{l}ax+by=5\\ \left(2-a\right)x+\left(3-b\right)y=4\end{array}\right.$ có nghiệm (–3; 4)

Lời giải:

$\left\{\begin{array}{l}ax+by=5\\ \left(2-a\right)x+\left(3-b\right)y=4\end{array}\right.$ có nghiệm (–3; 4)

$\iff \left\{\begin{array}{l}-3a+4b=5\\ (2-a).(-3)+(3-b).4=4\end{array}\right.\iff \left\{\begin{array}{l}3a-4b=-5\\ 3a-4b=-2\end{array}\right.$

Do đó, hệ phương trình vô nghiệm.

Vậy không có giá trị nào của a và b thỏa mãn yêu cầu đề bài

Câu 45: Một máy bơm bơm đầy bình nước hết 5 giờ , một máy bơm khác bơm đầy cùng bình đó hết 3 giờ. Hỏi nếu 2 máy bơm cùng nhau thì sau bao lâu thì đầy $\frac{2}{3}$ bình.

Lời giải:

Máy 1 trong 1 giờ bơm được: $\frac{1}{5}$ bình

Máy 2 trong 1 giờ bơm được: $\frac{1}{3}$ bình

Hai máy bơm 1h được $\frac{1}{5}+\frac{1}{3}=\frac{8}{15}$ (h)Tìm a, b để hệ phương trình  có nghiệm (–3; 4)

Vậy muốn bơm $\frac{2}{3}$ bình thì cần số thời gian là: $\frac{2}{3}:\frac{8}{15}=\frac{5}{4}\left(h\right)$

Câu 46: Cho tam giác ABC, M là điểm trên cạnh BC sao cho BM = 2MC. Chứng minh rằng: $AM=\frac{1}{3}AB+\frac{2}{3}AC$

Lời giải:

Vì MB = 2MC (M thuộc BC)

$$\begin{gathered} \Rightarrow \overrightarrow{MB}=-2\overrightarrow{MC} \\ \Rightarrow \overrightarrow{MA}+\overrightarrow{AB}=-2\overrightarrow{MA}-2\overrightarrow{AC} \\ \Rightarrow 3\overrightarrow{AM}=\overrightarrow{AB}+2\overrightarrow{AC} \\ \Rightarrow \overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC} \end{gathered}$$

Câu 47: 1. Hai điểm đối xứng qua một đường thẳng khi nào ?

2. Hai hình đối xứng qua một đường thẳng khi nào ?

3. Cho 1 số ví dụ về hình có trục đối xứng và chỉ ra trục đối xứng của nó.

Lời giải:

Khi đường thẳng d là đường trung trực của đoạn thẳng AB thì điểm A đối xứng với điểm B qua đường thẳng d. Khi đó đường thẳng d gọi là trục đối xứng của hai điểm A và B.

Câu 48: Mỗi người sử dụng máy tính dùng password có 6 đến 8 kí tự. Các ký tự có thể là chữ số hoặc chữ cái, mỗi password phải có ít nhất 01 chữ số. Tìm tổng số password có thể có.

Lời giải:

Phân biệt chữ thường với chữ hoa

Chữ cái thường: 26

Chữ cái hoa: 26

Chữ số: 10

Do đó, tổng cộng: 26 + 26 + 10 = 62 (ký tự khác nhau)

Nếu password có n ký tự thì ta có:

Tổng số trường hợp là: 62ⁿ

Số trường hợp không có chữ số là: 52²

Vậy số trường hợp có ít nhất 1 chữ số là: 62ⁿ – 52ⁿ

Với n = 6, 7, 8 ta có tổng số trường hợp là:

n = n₆ + n₇ + n₈ = 62⁶ – 52⁶ + 62⁷ – 52⁷ + 62⁸ – 52⁸

= 167410949583040.

Câu 49: Cho 4 điểm A, B, C, D. Gọi I, J lần lượt là trung điểm AB và CD. Chứng minh:

$\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}=2\overrightarrow{IJ}$

Lời giải:

Ta có: $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BC}+\overrightarrow{CD}$

$$\begin{gathered} =\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC} \\ =\overrightarrow{AI}+\overrightarrow{IJ}+\overrightarrow{JD}+\overrightarrow{BI}+\overrightarrow{IJ}+\overrightarrow{IC} \\ =2\overrightarrow{IJ}+\left(\overrightarrow{AI}+\overrightarrow{BI}\right)+\left(\overrightarrow{JD}+\overrightarrow{JC}\right)=2\overrightarrow{IJ} \end{gathered}$$

Câu 50: Giải phương trình: cos3x + cosx – cos2x = 0.

Lời giải:

cos3x + cosx – cos2x = 0

$$\begin{gathered} \iff 2\cos 2x.\cos x-\cos 2x=0 \\ \iff \cos 2x\left(2\cos x-1\right)=0 \\ \iff \left[\begin{array}{c}\cos 2x=0\\ 2\cos 2x-1=0\end{array}\right. \\ \iff \left[\begin{array}{c}2x=\frac{\pi }{2}+k\pi \\ \cos 2x=\cos \frac{\pi }{3}\end{array}\right. \\ \iff \left[\begin{array}{c}x=\frac{\pi }{4}+k\frac{\pi }{2}\\ x=\pm \frac{\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right) \end{gathered}$$