Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 60)

Câu 1: Một nhóm học sinh gồm 7 bạn nam và 4 nữ đứng ngẫu nhiên thành một hàng. Xác suất để có đúng 2 trong 4 bạn nữ đứng cạnh nhau là bao nhiêu?

Lời giải:

Xếp 7 bạn nam đứng thành hàng, có 7! cách (tạo ra 8 khoảng trống).

Chọn 2 nữ đứng cạnh nhau, có $C_4^2$  cách.

Chọn 3 khoảng trống trong 8 khoảng trống để xếp các nữ, có $A_8^3.2!$  cách.

Vậy xác suất cần tìm là: $\frac{C_4^2.2.7!.A_8^3}{11!}=\frac{28}{55}$ .

Câu 2: Số dư khi chia đa thức 3x⁴ – 2x³ + x² – 2x + 2 cho đa thức x – 2 là

A. 50;

B. 34;

C. 32;

D. 30.

Lời giải:

Đáp án đúng là: B

Ta có: 3x⁴ – 2x³ + x² – 2x + 2

= 3x⁴ – 6x³ + 4x³ – 8x² + 9x² – 18x + 16x – 32 + 34

= 3x³(x – 2) + 4x²(x – 2) + 9x(x – 2) + 16(x – 2) + 34

= (x – 2)(3x³ + 4x² + 9x + 16) + 34.

Vậy đa thức 3x⁴ – 2x³ + x² – 2x + 2  chia cho đa thức x – 2 được 3x³ + 4x² + 9x + 16 và dư 34.

Câu 3: Tìm số dư của phép chia (x + 2)(x + 3)(x + 4)(x + 5) + 2020 cho x² + 7x + 5.

Lời giải:

Ta có: A = (x + 2)(x + 3)(x + 4)(x + 5) + 2020

= [(x + 2)(x + 5)][(x + 3)(x + 4)] + 2020

= (x² + 7x + 20)(x² + 7x + 12) + 2020

Đặt a = x² + 7x + 5

Khi đó A = (a + 5)(a + 7) + 2020

= a² + 16a + 35 + 2020

= a(a + 16) + 2055

Do đó A = (x² + 7x + 5)(x² + 7x + 5 + 16) + 2055

= (x² + 7x + 5)(x² + 7x + 21) + 2055

Vậy phép chia (x + 2)(x + 3)(x + 4)(x + 5) + 2020 cho x² + 7x + 5 ta được thương là:

x² + 7x + 21 và dư 2055.

Câu 4: Viết phương trình tổng quát của trục hoành Ox.

Lời giải:

Ta có đường thẳng Ox đi qua O(0; 0) có vectơ pháp tuyến $\overrightarrow{n}=\left(0;1\right)$ nên có phương trình tổng quát là 0(x – 0) + 1(y – 0) = 0 ⇔ y = 0.

Vậy phương trình tổng quát của trục hoành Ox là y = 0.

Câu 5: Tính giá trị của biểu thức x³ – 6x² + 12x – 8 với x = 3.

A. 2;

B. 4;

C. 1;

D. 0.

Lời giải:

Đáp án đúng là: C

Ta có: x³ – 6x² + 12x – 8

= x³ – 3x².2 + 3.x.2² – 2³ = (x – 2)³      (1)

Thay x = 3 vào (1) ta có: (3 – 2)³ = 1.

Câu 6: Phân tích đa thức thành nhân tử:

a) x³ + 6x² + 12x + 8;

b) x³ – 3x² + 3x – 1.

Lời giải:

a) x³ + 6x² + 12x + 8

= x³ + 3.x².2 + 3.x.2² + 2³

= (x + 2)³.

b) x³ – 3x² + 3x – 1

= x³ – 3.x².1 + 3.x.1² – 1

= (x – 1)³.

Câu 7: Nêu công thức tính tổ hợp?

Lời giải:

Cho tập hợp A có n phần tử và số nguyên k với 1 ≤ k ≤ n.

Mỗi tập con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.

Kí hiệu $C_n^k$  là số tổ hợp chập k của n phần tử.

Công thức tính: $C_n^k=\frac{n!}{k!\left(n-k\right)!}$ .

Câu 8: Cho hai đường tròn (O; R) và (O’; r) với R > r, cắt nhau tại A và B. Vẽ hình bình hành OAO’M.

a) Chứng minh rằng BM // OO’.

b) Vẽ đường kính AOC. Chứng minh ba điểm B, M, C thẳng hàng.

Lời giải:

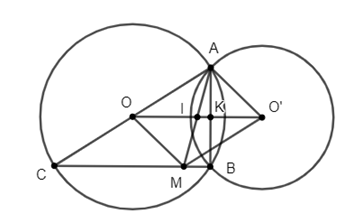
a) Vẽ dây cung AB cắt OO’ tại K.

Ta có KA = KB.

Gọi I là giao điểm của AM với OO’ thì IA = IM (tính chất đường chéo hình bình hành).

Xét ∆ABM thì IK là đường trung bình nên IK // BM hay BM // OO’ (1)

b) Xét ∆ABC có OK là đường trung bình nên OK // BC hay BC // OO’. (2)

Từ (1) và (2) và theo tiên đề Euclid, ta suy ra ba điểm B, M, C thẳng hàng.

Câu 9: Chứng minh rằng trong một tam giác ba phân giác của hai góc ngoài và một góc trong không kề với chúng gặp nhau tại một điểm.

Lời giải:

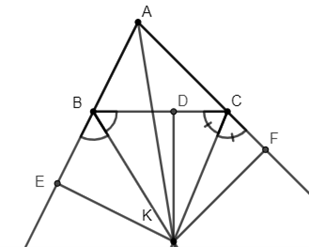
Gọi K là giao điểm của hai đường phân giác góc ngoài của góc B và góc C.

Từ K hạ KD, KE, KF lần lượt vuông góc với BC, AB, AC.

Theo tính chất về đường phân giác ta có: KD = KE; KD = KF

Suy ra KE = KF.

Do đó K nằm trên đường phân giác của $\widehat{BAC}$ .

Vậy hai phân giác góc ngoài của góc B và C và phân giác góc trong của góc A gặp nhau tại một điểm.

Câu 10: Nêu tính chất đường phân giác của tam giác.

Lời giải:

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

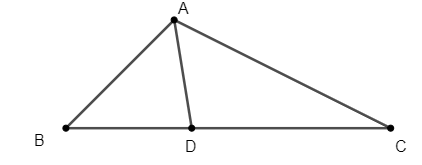
Giả thiết: ∆ABC có AD là đường phân giác của góc $\widehat{BAC}$  (D ∈ BC).

Kết luận: $\frac{DB}{DC}=\frac{AB}{AC}$ .

Câu 11: Cho phương trình bậc hai x² – 2(m – 1)x + m² – 3m – 4 = 0 (m là tham số, x là ẩn số). Tìm m để phương trình có hai nghiệm phân biệt x₁; x₂.

Lời giải:

Để phương trình có hai nghiệm phân biệt x₁; x₂ thì ∆’ > 0

⇔ (m – 1)² – (m² – 3m – 4) > 0

⇔ m² – 2m + 1 – m² + 3m + 4 > 0

⇔ m + 5 > 0

⇔ m > −5

Vậy với m > −5 thì phương trình đã cho có hai nghiệm phân biệt.

Câu 12: Cho phương trình: x² – 2(m – 1)x + m² – 3 = 0 (x là ẩn, m là tham số). Tìm m để phương trình có hai nghiệm x₁; x₂ sao cho x₁² +  4x₁ + 2x₂ – 2mx₁ = 1.

Lời giải:

Phương trình đã cho có hai nghiệm khi và chỉ khi:

∆’ ≥ 0 ⇔ −2m + 4 ≥ 0 ⇔ m ≤ 2 (1)

Theo hệ thức vi-ét ta có:

$\left\{\begin{array}{l}{x}_1+x_2=2(m-1)\\ x_1{x}_2=m^2-3\end{array}\right.$

Mà x₁² + 4x₁ + 2x₂ – 2mx₁ = 1

⇔ x₁(x₁ – 2m + 2) + 2(x₁ + x₂) = 1

⇔ −x₁x₂ + 2(x₁ + x₂) = 1

⇔ −m² + 3 + 4(m – 1) = 1

⇔ m² – 4m + 2 = 0

$\iff \left[\begin{array}{l}m=2+\sqrt{2}\\ m=2-\sqrt{2}\end{array}\right.$ (2)

Từ (1) và (2) suy ra $m=2-\sqrt{2}$ .

Câu 13: Tìm nguyên hàm của hàm số f(x) = 3x² + 8sinx.

A. F(x) = 6x – 8cosx + C;

B. F(x) = 6x + 8cosx + C;

C. F(x) = x³ – 8cosx + C.

D. F(x) = x³ + 8cosx + C.

Lời giải:

Đáp án đúng là: C

Ta có  $\int f\left(x\right)dx=3x^2+8\sin x$

$\iff \int f\left(x\right)dx=\int 3x^{2}dx+\int 8\sin xdx$ = x³ – 8cosx + C.

Câu 14: Cho hàm số f(x) = x³ + x² + 8x + cosx và hai số thực a, b sao cho a < b. Khẳng định nào sau đay là đúng?

A. f(a) = f(b);

B. f(a) > f(b);

C. f(a) < f(b);

D. Không so sánh được f(a) và f(b).

Lời giải:

Đáp án đúng là: C

Tập xác định D = ℝ

Ta có: f’(x) = 3x² + 2x + 8 – sinx = (3x² + 2x + 1) + (7 – sinx) > 0

Suy ra f(x) đồng biến trên ℝ. Do đó a < b ⇒ f(a) < f(b)

Câu 15: Cho a là số nguyên dương nhỏ nhất có hai chữ số chia hết cho 2 và 5; b là số nguyên âm lớn nhất có ba chữ số. Tính tổng a + b.

Lời giải:

Vì a chia hết cho 2 và 5 nên a có chữ số tận cùng là 0.

Hơn nữa a là số nguyên dương nhỏ nhất có hai chữ số nên a = 10.

Ta có b là số nguyên âm lớn nhất có ba chữ số nên b = −100.

Vậy tổng a + b = 10 + (−100) = −90.

Câu 16: Tìm số tự nhiên nhỏ nhất chia hết cho 3 và chia cho 4, 5, 6 đều dư 3.

Lời giải:

Gọi số tự nhiên nhỏ nhất chia hết cho 3 và chia cho 4, 5, 6 đều dư 3 là a

• a chia hết cho 3 nên tổng các chữ số của a là 1 số chia hết cho 3

• a chia 5 dư 3 nên a có chữ số hàng đơn vị là 3 hoặc 5

• a chia 4, 5, 6 dư 3 nên a − 3 chia hết cho 4, 5, 6

• a nhỏ nhất khi a − 3 nhỏ nhất

Số tự nhiên nhỏ nhất chia hết cho 4; 5; 6 là 60

Khi đó a − 3 = 60 hay a = 63.

Xét 63 chia hết cho 3 nên 63 thỏa mãn các yêu cầu của đề bài

Vậy số tự nhiên nhỏ nhất chia hết cho 3 và chia cho 4, 5, 6 đều dư 3 là số 63.

Câu 17: Tìm số tự nhiên nhỏ nhất chia cho cả 2; 3; 4; 5 và 6 đều dư 1.

Lời giải:

Gọi số tự nhiên nhỏ nhất chia cho cả 2; 3; 4; 5 và 6 đều dư 1 là a

• a chia cho cả 2; 3; 4; 5 và 6 đều dư 1 nên a − 1 chia hết cho 2; 3; 4; 5 và 6.

• a nhỏ nhất nên a − 1 nhỏ nhất.

Số tự nhiên nhỏ nhất chia hết cho 2; 3; 4; 5 và 6 là 60 nên a − 1 = 60.

Vậy a = 61.

Vậy số tự nhiên nhỏ nhất chia cho cả 2; 3; 4; 5 và 6 đều dư 1 là 61.

Câu 18: Phân tích đa thức thành nhân tử: x⁴ – 6x³ + 7x² + 6x – 8.

Lời giải:

x⁴ – 6x³ + 7x² + 6x – 8

= x⁴ – 2x³ – x² + 2x – 4x³ + 8x² + 4x – 8

= x³(x – 2) – x(x – 2) – 4x²(x – 2) + 4(x – 2)

= (x – 2)(x³ – x – 4x² + 4)

= (x – 2)[x²(x – 4) – (x – 4)]

= (x – 2)(x – 4)(x² – 1)

= (x – 2)(x – 4)(x – 1)(x + 1)

Câu 19: Phân tích đa thức thành nhân tử x⁵ + x + 1.

Lời giải:

x⁵ + x + 1 = (x⁵ – x⁴ + x²) + (x⁴ – x³ + x) + (x³ – x² + 1)

= x²(x³ – x² + 1) + x(x³ – x² + 1) + (x³ – x² + 1)

= (x³ – x² + 1)(x² + x + 1)

Câu 20: Phân tích đa thức thành nhân tử: (x² – 8)² + 36.

Lời giải:

(x² – 8)² + 36 = x⁴ – 16x² + 64 + 36

= x⁴ – 16x² + 100

= (x⁴ + 20x² + 100) – 36x²

= (x² + 10)² – (6x)²

= (x² – 6x + 10)(x² + 6x + 1)

Câu 21: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O, góc quay a ≠ kπ, k ∈ ℤ?

A. Không có;

B. 1;

C. 2;

D. Vô số

Lời giải:

Đáp án đúng là: B

Điểm M biến thành chính nó qua phép quay tâm O, góc quay a ≠ kπ, k ∈ ℤ khi M trùng với tâm O.

Câu 22: Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807 200 người. Tính số dân năm ngoái của mỗi tỉnh.

Lời giải:

Gọi x (triệu người) là số dân năm ngoái của tỉnh A (0 < x < 4; x ∈ ℕ*)

Số dân năm ngoái của tỉnh B là: 4 – x (triệu người).

Năm nay dân số của tỉnh A tăng 1,1% nên số dân của tỉnh A năm nay là:

x + 1,1% x = 1,011.x (triệu người).

Năm nay dân số của tỉnh B tăng 1,2% nên số dân của tỉnh B năm nay là:

(4 – x) + 1,2% (4 – x) = 1,012(4 – x) (triệu người).

Vì số dân tỉnh A năm nay hơn tỉnh B là 807 200 người hay 0,8072 triệu người nên ta có phương trình:

1,011.x – 1,012(4 – x) = 0,8072

⇔ 1,011x – 4,048 + 1,012x = 0,8072

⇔ 1,011x + 1,012x = 0,8072 + 4,048

⇔ 2,023x = 4,8552

⇔ x = 2,4 (thỏa mãn).

Vậy dân số của tỉnh A năm ngoái là 2,4 triệu người, dân số tỉnh B năm ngoái là

4 – 2,4 = 1,6 (triệu người).

Câu 23: Phân tích đa thức thành nhân tử: x² – y² + 4x + 4.

Lời giải:

x² – y² + 4x + 4

= (x² + 4x + 4) – y²

= (x + 2)² – y²

= (x + 2 + y)(x + 2 – y)

= (x + y + 2)( x – y + 2)

Câu 24: Phân tích đa thức thành nhân tử: x² – 14x + 49 – 4y².

Lời giải:

x² – 14x + 49 – 4y²

= (x² – 14x + 49) – 4y²

= (x – 7)² – (2y)²

= (x – 7 – 2y)(x – 7 + 2y)

Câu 25: Nêu công thức định lý cosin.

Lời giải: Cho tam giác ABC có AB = c, BC = a, AC = b. Khi đó:

a² = b² + c² – 2bc.cosA;

b² = a² + c² – 2ac.cosB;

c² = a² + b² – 2ab.cosC.

Câu 26: Có bao nhiêu phép quay với góc quay a (0° < a < 360°) biến tam giác đều cho trước thành chính nó?

A. 0;

B. 1;

C. 2;

D. 4.

Lời giải:

Đáp án đúng là: C

Tồn tại hai phép quay góc quay a:

+) Q_{(G; 120°)} (∆ABC) = (∆ABC).

+) Q_{(G; 240°)} (∆ABC) = (∆ABC).

Với G là trong tam giác ABC.

Câu 27: Phân tích đa thức thành nhân tử: x²(1 – x²) – 4 – 4x².

Lời giải:

x²(1 – x²) – 4 – 4x²

= −x⁴ + x² – 4 – 4x²

= −[(x⁴ + 4x² + 4) – x²]

= −[(x² + 2)² – x²]

= −(x² + 2 + x)(x² + 2 – x)

Câu 28: Cho a, b ∈ ℝ. Chứng minh rẳng: 2(a⁴ + b⁴) ≥ ab³ + a³b + 2a²b².

Lời giải:

Ta có: 2(a⁴ + b⁴) ≥ ab³ + a³b + 2a²b²

⇔ a⁴ – 2a²b² + b⁴ + a⁴ – a³b + b⁴ – ab³ ≥ 0

⇔ (a² – b²)² + a³(a – b) – b³(a – b) ≥ 0

⇔ (a² – b²)² + (a³ – b³)(a – b) ≥ 0

⇔ (a – b)²[(a + b)² + (a² + ab + b²)] ≥ 0

⇔ (a – b)²[3(a + b)² + a² + b²] ≥ 0

Dấu “=” xảy ra khi a = b.

Câu 29: Chứng minh rằng: 1 + 2 + 2² + … + 2⁹⁹ + 2¹⁰⁰ = 2¹⁰¹ – 1.

Lời giải:

Đặt A = 1 + 2 + 2² + … + 2⁹⁹ + 2¹⁰⁰.

Ta có: 2 A = 2 + 2² + … + 2¹⁰⁰ + 2¹⁰¹.

Khi đó 2A – A = (2 + 2² + … + 2¹⁰⁰ + 2¹⁰¹) – (1 + 2 + 2² + … + 2⁹⁹ + 2¹⁰⁰)

= 2 + 2² + … + 2¹⁰⁰ + 2¹⁰¹ – 1 – 2 – 2² – … – 2⁹⁹ – 2¹⁰⁰

= (2 – 2) + (2² – 2²) + (2⁹⁹– 2⁹⁹) +… + (2¹⁰⁰ – 2¹⁰⁰) + 2¹⁰¹ – 1

= 2¹⁰¹ – 1 (đpcm)

Câu 30: Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.

Lời giải:

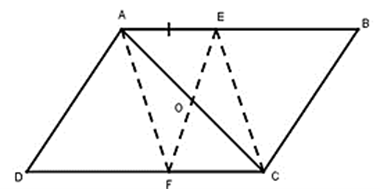
Gọi O là giao điểm của hai đường chéo AC và BD.

Xét tứ giác AECF:

AB // CD (gt)

⇒ AE // CF

AE = CF (gt)

Suy ra tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Do đó AC và EF cắt nhau tại trung điểm mỗi đường.

Vì OA = OC (tính chất hình bình hành) nên EF đi qua O.

Vậy AC, BD, EF đồng quy tại O.

Câu 31: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE = CF. Gọi O là giao điểm của AC và BD.

a) Chứng minh tứ giác AECF là hình bình hành.

b) Chứng minh O là trung điểm của EF.

Lời giải:

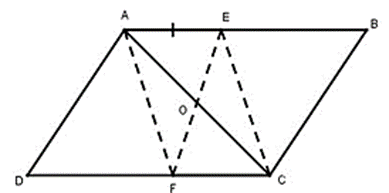
a) Gọi O là giao điểm của hai đường chéo AC và BD.

Xét tứ giác AECF có AB // CD (gt)

Suy ra AE // CF

AE = CF (gt)

Suy ra tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

b) Tứ giác AECF là hình bình hành nên AC và EF cắt nhau tại trung điểm mỗi đường.

Mà O là trung điểm của AC (tính chất hình bình hành).

Do đó EF đi qua O và O cũng là trung điểm của cạnh EF.

Câu 32: Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF qua phép quay tâm O góc quay 120°.

Lời giải:

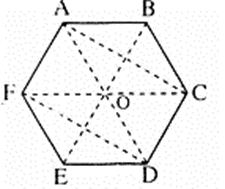
• Ảnh của điểm A qua phép quay tâm O góc quay 120° là E.

• Ảnh của điểm O qua phép quay tâm O góc quay 120° là O.

• Ảnh của điểm F qua phép quay tâm O góc quay 120° là D.

Vậy ảnh của tam giác AOF qua phép quay tâm O góc quay 120° là tam giác EOD.

Câu 33: Cho lục giác đều ABCDEF như hình vẽ.

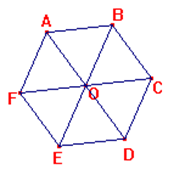
Phép quay tâm O góc 120° biến tam giác AOE thành tam giác nào?

Lời giải:

• Ảnh của điểm A qua phép quay tâm O góc quay 120° là E.

• Ảnh của điểm O qua phép quay tâm O góc quay 120° là O.

• Ảnh của điểm E qua phép quay tâm O góc quay 120° là C.

Vậy ảnh của tam giác AOE qua phép quay tâm O góc quay 120° là tam giác EOC.

Câu 34: Phân tích đa thức x² − 5x + 6 thành nhân tử.

Lời giải:

x² − 5x + 6 = x² − 2x − 3x + 6

= x(x − 2) − 3(x − 2)

= (x − 2)(x − 3)

Câu 35: Phân tích đa thức x² − 5x − 6 thành nhân tử.

Lời giải:

x² − 5x – 6 = x² + x − 6x − 6

= x(x + 1) − 6(x + 1)

= (x + 1)(x − 6)

Câu 36: Tìm số tự nhiên n sao cho p = (n − 2).(n² + n − 5) là số nguyên tố.

Lời giải:

Để tích của hai số tự nhiên là một số nguyên tố thì một trong hai thừa số phải bằng 1.

• TH1: n − 2 = 1 ⇔ n = 3

⇒ p = (3 − 2)(3² + 3 − 5) = 7 là số nguyên tố.

Vậy n = 3 thỏa mãn.

• TH2: n² + n − 5 = 1 mà n là số tự nhiên suy ra n = 2

⇒ p = (2 − 2).(2² + 2 − 5) = 0 không là số nguyên tố.

Vậy n = 2 không thỏa mãn.

Vậy số tự nhiên n cần tìm là n = 3.

Câu 37: Tìm số tự nhiên n để số p là số nguyên tố biết p = n³ − n² + n – 1.

Lời giải:

Ta có: p = n³ − n² + n − 1 = n²(n − 1) + (n − 1) = (n − 1)(n² + 1)

Để tích của hai số tự nhiên là một số nguyên tố thì một trong hai thừa số phải bằng 1.

• TH1: n − 1 = 1 ⇔ n = 2

⇒ p = (2 − 1)(2² + 1) = 5 là số nguyên tố

Vậy n = 2 thỏa mãn.

• TH2: n² + 1 = 1 ⇔ n = 0

⇒ p = (0 − 1)(0 + 1) = −1 không là số nguyên tố

Vậy n = 0 không thỏa mãn.

Vậy số tự nhiên n cần tìm là n = 2

Khi đó, p = 5 là số nguyên tố.

Câu 38: Tính nhanh giá trị của đa thức: 3(x − 3)(x + 7) + (x − 4)² + 48 tại x = 0,5.

Lời giải:

3(x − 3)(x + 7) + (x − 4)² + 48

= 3x² + 12x + x² − 8x + 64

= 4x² + 4x + 1 = (2x + 1)².

Tại x = 0,5 thì giá trị của đa thức là: (2.0,5 + 1)² = 2² = 4.

Câu 39: Phân tích đa thức x² − y² − x + y thành nhân tử.

Lời giải:

x² − y² − x + y

= (x − y)(x + y) − (x − y)

= (x − y)(x + y − 1).

Câu 40: Cho hàm số f (x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?

A. Nếu f ‘(x) < 0 với mọi x thuộc (a; b) thì hàm số f (x) nghịch biến trên (a; b);

B. Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) > 0 với mọi x thuộc (a; b);

C. Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) ≥ 0 với mọi x thuộc (a; b);

D. Nếu f ‘(x) > 0 với mọi x thuộc (a; b) thì hàm số f (x) đồng biến trên (a; b).

Lời giải:

Đáp án đúng là: B

• Nếu f ‘(x) > 0 với mọi x thuộc (a; b) thì hàm số f (x) đồng biến trên (a; b).

Vậy mệnh đề D là đúng.

• Nếu f ‘(x) < 0 với mọi x thuộc (a; b) thì hàm số f (x) nghịch biến trên (a; b).

Vậy mệnh đề A là đúng.

• Nếu hàm số f (x) đồng biến trên (a; b) thì f (x) ≥ 0 với mọi x thuộc (a; b).

Vậy mệnh đề B là sai và mệnh đề C là đúng.

Chọn đáp án B.

Câu 41: Cho hàm số f (x) xác định và có đạo hàm trên khoảng (a; b). Nếu f ‘(x) < 0, ∀x ∈ (a; b) thì:

A. Hàm số đồng biến trên (a; b);

B. Hàm số nghịch biến trên (a; b);

C. Hàm số không đổi trên (a; b);

D. Hàm số vừa đồng biến vừa nghịch biến trên (a; b).

Lời giải:

Đáp án đúng là: B

Hàm số f (x) xác định và có đạo hàm trên khoảng (a; b). Nếu f ‘(x) < 0, ∀x ∈ (a; b) thì hàm số nghịch biến trên (a; b).

Chọn đáp án B.

Câu 42: Trong các hàm số sau đây, hàm số nào có đồ thị đối xứng qua trục tung?

A. y = sin x;

B. y = tan x;

C. y = cot x;

D.  y = cos x.

Lời giải:

Đáp án đúng là: B

Trong 4 đáp án trên, hàm số y = cos x là hàm chẵn do cos x = cos (−x).

Vậy y = cos x có đồ thị hàm số đối xứng qua trục tung.

Chọn đáp án B.

Câu 43: Phân tích đa thức x² − x − y² − y thành nhân tử.

Lời giải:

Ta có: x² − x − y² − y

= (x² − y²) − (x + y)

= (x − y)(x + y) − (x + y)

= (x − y − 1)(x + y)

Câu 44: Phân tích đa thức sau thành nhân tử: x² + x − y² + y.

Lời giải:

Ta có: x² + x − y² + y

= (x² − y²) + (x + y)

= (x − y)(x + y) + (x + y)

= (x − y + 1)(x + y).

Câu 45: Phân tích các đa thức sau thành nhân tử:

a) x² − 5x − 14

b) 4x² − 3x − 1

c) x⁴ + 64

Lời giải:

a) x² − 5x − 14

= x² − 7x + 2x − 14

= x(x − 7) + 2(x − 7)

= (x − 7)(x + 2)

b) 4x² − 3x − 1

= 4x² − 4x + x − 1

= 4x(x − 1) + (x − 1)

= (x − 1)(4x + 1)

c) x⁴ + 64

= x⁴ + 16x² + 64 − 16x²

= (x² + 8)² − (4x)²

= (x² + 8 − 4x)(x² + 8 + 4x)

= (x² − 4x + 8)(x² + 4x + 8)

Câu 46: Cho a, b, c là các số không âm thỏa mãn: a + b + c = 1. Chứng minh rằng:

b + c ≥ 16abc.

Lời giải:

Áp dụng BĐT Cauchy, ta có:

(a + b + c)² ≥ 4a(b + c)

(b + c)² ≥ 4bc

Nhân từng vế, ta có: (a + b + c)² . (b + c)² ≥ 4a(b + c) . 4bc.

Do đó b + c ≥ 16bc.

Dấu “=” xảy ra khi và chỉ khi $\left\{\begin{array}{l}a=\frac{1}{2}\\ b=c=\frac{1}{4}\end{array}\right.$ .

Vậy b + c ≥ 16abc (đpcm).