Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 22)

Admin Vietjack Ngày: 26-07-2023 Tổng hợp kiến thức

1.2 K

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 22)

Câu 1: Giải phương trình: cos3x.cosx = cos2x.

Lời giải:

cos3x.cosx = cos2x

$\Leftrightarrow \frac{1}{2} (\cos 4 x + \cos 2 x) = \cos 2 x \Leftrightarrow \cos 4 x = \cos 2 x \Leftrightarrow 2 \cos^{2} 2 x - 1 - \cos 2 x = 0 \Leftrightarrow [\begin{matrix} \cos 2 x = 1 \\ \cos 2 x = - \frac{1}{2} \end{matrix}$

Với cos2x = 1 $\Rightarrow x = k π (k \in ℤ)$ .

Với cos2x = $- \frac{1}{2} \Rightarrow [\begin{matrix} x = \frac{π}{3} + k π \\ x = - \frac{π}{3} + k π \end{matrix} (k \in ℤ)$ .

Câu 2: Tính ${(a - b - c)}^{3}$ .

Lời giải:

Ta có:

${(a - b - c)}^{3} = {[(a - b) - c]}^{3} = {(a - b)}^{3} - 3 {(a - b)}^{2} c + 3 (a - b) c^{2} - c^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} - 3 c (a^{2} - 2 a b + b^{2}) + 3 a c^{2} - 3 b c^{2} - c^{3} = a^{3} - b^{3} - c^{3} - 3 a b (a - b) - 3 a c (a - c) - 3 b c (b + c) + 6 a b c$

Câu 3: Giải hệ phương trình: $\{\begin{matrix} x^{4} + 2 x^{3} y + x^{2} y^{2} = 2 x + 9 \\ x^{2} + 2 x y = 6 x + 6 \end{matrix}$ .

Lời giải:

Hệ phương trình đã cho tương đương với:

$\{\begin{matrix} {(x^{2} + x y)}^{2} = 2 x + 9 \\ x y = 3 x + 3 - \frac{x^{2}}{2} \end{matrix} \Rightarrow {(x^{2} + 3 x + 3 - \frac{x^{2}}{2})}^{2} = 2 x + 9 \Leftrightarrow x^{4} + 12 x^{3} + 48 x^{2} + 64 x = 0 \Leftrightarrow x {(x + 4)}^{3} = 0 \Leftrightarrow [\begin{matrix} x = 0 \\ x = - 4 \end{matrix}$

+) x = 0 không thỏa mãn hệ phương trình.

+) x = –4 $\Rightarrow y = \frac{17}{4}$

Nghiệm của hệ phương trình là $(x; y) = (- 4; \frac{17}{4})$

Câu 4: Hình vuông có cạnh bằng 2 thì đường chéo hình vuông đó bằng bao nhiêu?

Lời giải:

Giả sử hình vuông ABCD độ dài cạnh 2, đường chéo AC chia hình vuông thành 2 tam giác ABC và ACD. Áp dụng định lí Pytago cho tam giác vuông ABC:

$A C^{2} = A B^{2} + B C^{2}$

Hay $A C^{2} = 2^{2} + a^{2} = {2.2}^{2} \Rightarrow A C = a \sqrt{2}$

Vậy đường chéo hình vuông có độ dài cạnh a là 2 $\sqrt{2}$ .

Câu 5: Chứng minh $A \cup B = A \cap B$ thì A = B.

Lời giải:

Gọi x là phần tử bất kì thuộc tập A

$x \in A \Rightarrow x \in A \cup B .$ Mà $A \cup B = A \cap B$ nên x $\in A \cap B \Rightarrow x \in B$

A là tập con của B(1)

Gọi y là phần tử bất kì thuộc tập B.

$\Rightarrow y \in A \cup B .$ Mà $A \cup B = A \cap B$ nên y $\in A \cap B \Rightarrow y \in A$

$\Rightarrow B$ là tập con của A(2)

Từ (1) và (2) ⇒ A = B (đpcm).

Câu 6: Xác định các tập hợp A $\cup B$ và $A \cap B$ với: A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.

Lời giải:

Ta có tập A ∪ B là tập các phần tử thuộc tập A hoặc thuộc tập B nên A ∪ B = {đỏ; cam; vàng; lục; lam; tràm; tím}.

Tâp hợp $A \cap B$ là tập các phần tử vừa thuộc tập A vừa thuộc B nên $A \cap B =$ {lục; lam}.

Vậy A ∪ B = {đỏ; cam; vàng; lục; lam; tràm; tím} và A ∩ B = {lục; lam}.

Câu 7: Cho $Δ A B C$ đều cạnh a. Tính độ dài vectơ $\vec{A B} - \vec{A C}$ và $\vec{A B} + \vec{A C}$ .

Lời giải:

$\vec{A B} - \vec{A C} = \vec{C B} \Rightarrow |\vec{A B} - \vec{A C}| = |\vec{C B}| = a$

$\vec{A B} + \vec{A C} = \vec{A A^{'}} = 2 \vec{A M}$ (ABA’C là hình bình hành, M là trung điểm của BC, nên M cũng là trung điểm của AA’)

$|\vec{A B} + \vec{A C}| = 2 A M = 2. \frac{a \sqrt{3}}{2} = a \sqrt{3}$ .

Câu 8: Cho phương trình: $\cos (2 x - \frac{π}{3}) - m = 2$ . Tìm m để phương trình có nghiệm.

Lời giải:

$\cos (2 x - \frac{π}{3}) - m = 2 \Leftrightarrow \cos (2 x - \frac{π}{3}) = m + 2$

PT trên có nghiệm

$\Leftrightarrow |m + 2| \leq 1 \Leftrightarrow - 1 \leq m + 2 \leq 1 \Leftrightarrow - 3 \leq m \leq - 1$

Câu 9: Giải phương trình sinxcosx + 2(sinx + cosx) = 2.

Lời giải:

Đặt t = sinx + cosx = $\sqrt{2} \sin (x + \frac{π}{4})$

Vì $\sin (x + \frac{π}{4}) \in [- 1; 1] \Rightarrow t \in [- \sqrt{2}; \sqrt{2}]$

Ta có

$t^{2} = {(\sin x + \cos x)}^{2} = \sin^{2} x + \cos^{2} x + 2 \sin x \cos x \Rightarrow \sin x \cos x = \frac{t^{2} - 1}{2}$

Khi đó, phương trình đã cho trở thành:

$\frac{t^{2} - 1}{2} + 2 t = 2 \Leftrightarrow t^{2} + 4 t - 5 \Leftrightarrow [\begin{matrix} t = 1 \\ t = - 5 (l) \end{matrix}$

Với t = 1, ta được sinx + cosx = 1 $\Leftrightarrow \sin (x + \frac{π}{4}) = \frac{1}{\sqrt{2}} \Leftrightarrow \sin (x + \frac{π}{4}) = \sin \frac{π}{4}$

$\Leftrightarrow [\begin{matrix} x + \frac{π}{4} = \frac{π}{4} + k 2 π \\ x + \frac{π}{4} = π - \frac{π}{4} + k 2 π \end{matrix} \Leftrightarrow [\begin{matrix} x = k 2 π \\ x = \frac{π}{2} + k 2 π \end{matrix}, k \in ℤ$

Câu 10: Một cánh đồng lúa thực nghiệm hình chữ nhật có chiều dài 1200m, chiều rộng bằng $\frac{3}{5}$ chiều dài. Người ta cấy giống lúa với năng xuất đạt 5 tấn trên 1 ha. Hỏi cả cánh đồng lúa thực nghiệm đó sẽ thu hoạch được bao nhiêu tấn thóc?

Lời giải:

Chiều rộng cánh đồng là: $1200. \frac{3}{5} = 720 (m)$

Diện tích cánh đồng là: 1200 x 720 = 864000

$864000 m^{2} = 86,4 h a$

Cánh đồng lúa thu hoạch được là: 86,4 × 5 = 432 (tấn).

Câu 11: Phân tích đa thức sau thành nhân tử: x² – 6x – 7.

Lời giải:

Ta có:

$x^{2} - 6 x - 7 = x^{2} + x - 7 x - 7 = x (x + 1) - 7 (x + 1) = (x + 1) (x - 7)$

Câu 12: Chứng minh phương trình sau có nghiệm: $x^{3} - 2 x - 1 = 0$ .

Lời giải:

Đặt f(x) = $x^{3} - 2 x - 1$

Ta có: f(0) = –1, f(2) = 3

Do f(0).f(2) < 0 nên tồn tại a ∈ (0, 2) sao cho f(a) = 0.

Vậy phương trình luôn có nghiệm.

Câu 13: Cho ∆ABC có CB = 2, CA = 3 và $\hat{A C B} = 90 °$ . Tính độ dài cạnh AB.

Lời giải:

Áp dụng công thức $c = \sqrt{a^{2} + b^{2}}$ vào tam giác đã cho ta được $A B = \sqrt{2^{2} + 3^{2}} = \sqrt{13}$ .

Vậy độ dài của cạnh cần tìm là $\sqrt{13}$ .

Câu 14: Tìm GTLN của hàm số y = 6sin2x – 8cos2x – 2.

Lời giải:

y = 6sin2x – 8cos2x – 2

$= 10 (\frac{3}{5} \sin 2 x - \frac{4}{5} \cos 2 x) - 2$

Đặt $\cos α = \frac{3}{5}; \sin α = \frac{4}{5}$

Khi đó

y = 10(cosα sin2x – sinα cos2x) – 2 = 10sin(2x – α) – 2

Ta có: –1 ≤ sin(2x – α) ≤ 1

$\Leftrightarrow - 10 \leq 10 \sin (2 x - α) \leq 10 \Leftrightarrow - 12 \leq y \leq 8 (\forall x \in ℝ)$

$M a x_{y} = 8$ khi sin(2x – α) = 1

$\Leftrightarrow 2 x - α = \frac{π}{2} + k 2 π \Leftrightarrow x = \frac{π}{4} + \frac{α}{2} + k π (k \in ℤ)$

Câu 15: Giải phương trình sau: $\cos^{2} 2 x = \frac{1}{4}$ .

Lời giải:

$\cos^{2} 2 x = \frac{1}{4} \Leftrightarrow [\begin{matrix} \cos 2 x = \frac{1}{2} \\ \cos 2 x = - \frac{1}{2} \end{matrix} \Leftrightarrow [\begin{matrix} 2 x = \pm k 2 π \\ 2 x = \pm \frac{2 π}{3} + k 2 π \end{matrix} (k \in ℤ) \Leftrightarrow [\begin{matrix} x = \pm \frac{π}{6} + k π \\ x = \pm \frac{π}{3} + k π \end{matrix} (k \in ℤ)$

Vậy phương trình có 4 họ nghiệm $\{\frac{\pm π}{3} + k π; \frac{\pm π}{6} + k π\} (k \in ℤ)$ .

Câu 16: Giải phương trình: cos2x – 3cosx + 2 = 0.

Lời giải:

cos2x – 3cosx + 2 = 0

$\Leftrightarrow 2 \cos^{2} x - 1 - 3 \cos x + 2 = 0$

$\Leftrightarrow 2 \cos^{2} x - 3 \cos x + 1 = 0 \Leftrightarrow [\begin{matrix} \cos x = 1 \\ \cos x = \frac{1}{2} = \cos \frac{π}{3} \end{matrix} \Leftrightarrow [\begin{matrix} x = k 2 π \\ x = \pm \frac{π}{3} + k 2 π \end{matrix} (k \in ℤ)$

Vậy $S = \{k 2 π; \pm \frac{π}{3} + k 2 π, k \in ℤ\}$ .

Câu 17: Giải phương trình: $\cos^{2} x + 3 \cos x + 2 = 0$ .

Lời giải:

$\cos^{2} x + 3 \cos x + 2 = 0 \Leftrightarrow \cos = - 1$ hay cosx = –2 (VN)

$\Leftrightarrow x = π + k 2 π (k \in ℤ)$

Vậy phương trình có nghiệm là: x = $π + k 2 π (k \in ℤ)$

Câu 18: Giải phương trình: cos4x + cos2x + 1 = 0.

Lời giải:

cos4x + cos2x + 1 = 0

$\Leftrightarrow 2 \cos^{2} 2 x - 1 + \cos 2 x + 1 = 0 \Leftrightarrow 2 \cos^{2} 2 x + \cos 2 x = 0 \Leftrightarrow \cos 2 x (2 \cos 2 x + 1) = 0 \Leftrightarrow [\begin{matrix} \cos 2 x = 0 (1) \\ 2 \cos 2 x + 1 = 0 (2) \end{matrix} (1) \Leftrightarrow 2 x = \frac{π}{2} + k π (k \in ℤ) \Leftrightarrow x = \frac{π}{4} + k \frac{π}{2} (k \in ℤ) (2) \Leftrightarrow \cos 2 x = - \frac{1}{2} = \cos \frac{2 π}{3} \Leftrightarrow [\begin{matrix} 2 x = \frac{2 π}{3} + k 2 π \\ 2 x = - \frac{2 π}{3} + k 2 π \end{matrix} (k \in ℤ) \Leftrightarrow [\begin{matrix} x = \frac{π}{3} + k π \\ x = - \frac{π}{3} + k π \end{matrix} (k \in ℤ)$

Câu 19: Giải phương trình: 1 + cos4x = cos2x.

Lời giải:

1 + cos4x = cos2x

$\Leftrightarrow 1 + 2 \cos^{2} 2 x - 1 = \cos 2 x \Leftrightarrow 2 \cos^{2} 2 x - \cos 2 x = 0 \Leftrightarrow [\begin{matrix} \cos 2 x = 0 \\ \cos 2 x = \frac{1}{2} \end{matrix} \Leftrightarrow [\begin{matrix} 2 x = \frac{π}{2} + k π \\ 2 x = \pm \frac{π}{3} + k 2 π \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{π}{4} + k \frac{π}{2} \\ x = \pm \frac{π}{6} + k π \end{matrix} (k \in ℤ)$

Câu 20: Giải phương trình tanx = cotx.

Lời giải:

ĐKXĐ: $\{\begin{matrix} \sin x \neq 0 \\ \cos x \neq 0 \end{matrix} \Rightarrow \sin 2 x \neq 0 \Leftrightarrow 2 x \neq k π \Leftrightarrow x \neq \frac{k π}{2} (k \in ℤ)$

tanx = cotx

$\Leftrightarrow \tan x = \frac{1}{\tan x} \Leftrightarrow \tan^{2} x = 1 \Leftrightarrow [\begin{matrix} \tan x = 1 \\ \tan x = - 1 \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{π}{4} + k π \\ x = - \frac{π}{4} + k π \end{matrix} \Rightarrow x = \frac{π}{4} + k \frac{π}{2} (k \in ℤ)$

Câu 21: Giải phương trình: $2 \sin^{2} x + \sin x \cos x - \cos^{2} x = 0$ .

Lời giải:

TH1: Nếu cosx = 0 là nghiệm của phương trình đã cho: cosx = 0 $\Leftrightarrow \sin^{2} x = 1$ không thỏa mãn phương trình.

TH2: cosx ≠ 0, chia cả 2 vế của phương trình cho $\cos^{2} x$ ta được:

$2 \tan^{2} x + \tan x - 1 = 0 \Leftrightarrow [\begin{matrix} \tan x = - 1 \\ \tan x = \frac{1}{2} \end{matrix} \Leftrightarrow [\begin{matrix} x = - \frac{π}{4} + k π \\ x = \arctan \frac{1}{2} + k π \end{matrix} (k \in ℤ)$

Câu 22: Cho một số có ba chữ số biết rằng khi viết thêm chữ số 5 vào bên phải số đó thì số đó tăng thêm 2444 đơn vị. Tìm số đó.

Lời giải:

Gọi số đó là abc

Ta có: abc5 = abc + 2444

⟺ 10(100a + 10b + c) + 5 = 100a + 10b + c + 2444

⟺ 9(100a + 10b + c) = 2439

⟺ 100a + 10b + c = 271 ⟺ abc = 271.

Câu 23: Giải phương trình: $x^{2} - y^{2} + 2 x - 4 y - 10 = 0$ với x, y nguyên dương.

Lời giải:

PT $\Leftrightarrow (x^{2} + 2 x + 1) - (y^{2} + 4 y + 4) = 7$

$\Leftrightarrow {(x + 1)}^{2} - {(y + 2)}^{2} = 7 \Leftrightarrow (x + y + 3) (x - y - 1) = 7$

Mặt khác, x, y > 0 ⇒ x + y + 3 > x – y – 1 và x + y +3 > 0

Nên ta có cặp nghiệm duy nhất sau: $\{\begin{matrix} x + y + 3 = 7 \\ x - y - 1 = 1 \end{matrix} \Leftrightarrow \{\begin{matrix} x + y = 4 \\ x - y = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 3 \\ y = 1 \end{matrix}$ .

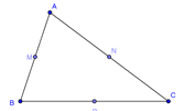
Câu 24: Tia đối của tia NM là ?

Tài liệu VietJack

Lời giải:

Hai tia đối nhau là hai tia có chung gốc tạo thành một đường thẳng nhất định.

⇒ Tia đối của tia NM là tia có chung gốc N với tia NM và tạo thành một đường thẳng.

⇒ Tia NP là tia đối của tia NM.

Câu 25: Giải phương trình: $2 x^{2} - 2 x - 3 = 0$ .

Lời giải:

$2 x^{2} - 2 x - 3 = 0 \Leftrightarrow x^{2} - x - \frac{3}{2} = 0 \Leftrightarrow x^{2} - x + \frac{1}{4} - \frac{7}{4} = 0 \Leftrightarrow {(x - \frac{1}{2})}^{2} = \frac{7}{4} \Leftrightarrow [\begin{matrix} x - \frac{1}{2} = \frac{\sqrt{7}}{2} \\ x - \frac{1}{2} = - \frac{\sqrt{7}}{2} \end{matrix} \Leftrightarrow [\begin{matrix} x = \frac{\sqrt{7} + 1}{2} \\ x = - \frac{\sqrt{7} - 1}{2} \end{matrix}$

Câu 26: Phân tích đa thức thành nhân tử: $4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2}$ .

Lời giải:

Ta có:

$4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2} = (2 a b + a^{2} + b^{2} - c^{2}) (2 a b - a^{2} - b^{2} + c^{2}) = ({(a + b)}^{2} - c^{2}) (c^{2} - {(a - b)}^{2}) = (a + b + c) (a + b - c) (c + a - b) (c - a + b)$

Câu 27: Cho $A = 4 a^{2} b^{2} - (a^{2} + b^{2} - c^{2})$ . Trong đó a, b, c là độ dài 3 cạnh của 1 tam giác. Chứng minh A > 0.

Lời giải:

$A = 4 a^{2} b^{2} - {(a^{2} + b^{2} - c^{2})}^{2} = (2 a b - a^{2} - b^{2} + c^{2}) (2 a b + a^{2} + b^{2} - c^{2}) \begin{array}{l} = [c^{2} - {(a - b)}^{2}] [{(a + b)}^{2} - c^{2}] \\ = (c - a + b) (c + a - b) (a + b + c) (a + b - c) \end{array}$

Vì a, b, c là ba cạnh của tam giác nên theo bất đẳng thức tam giác thì ta có:

b + c – a > 0, a + c – b > 0, a + b – c > 0

Lại có: a + b + c > 0

Vậy A > 0.

Câu 28: Với mọi số thực a, b, c. Chứng minh rằng: $a^{2} + 5 b^{2} - 4 a b + 2 a - 6 b + 3 > 0$ .

Lời giải:

$\begin{array}{l} a^{2} + 5 b^{2} - 4 a b + 2 a - 6 b + 3 \\ = a^{2} - 4 a b + 4 b^{2} + 2 a - 4 b + 1 + b^{2} - 2 b + 1 + 1 \end{array} \begin{array}{l} = {(a - 2 b)}^{2} + 2 (a - 2 b) + 1 + {(b - 1)}^{2} + 1 \\ = {(a - 2 b + 1)}^{2} + {(b - 1)}^{2} + 1 > 0 \end{array}$

Câu 29: Giải phương trình: sin2x.cotx = 0.

Lời giải:

PT $\Leftrightarrow 2 \sin x . \cos x . \frac{\cos x}{\sin x} = 0 \Leftrightarrow 2 \cos^{2} x = 0$

$\Leftrightarrow \cos^{2} x = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π (k \in ℤ)$

Câu 30: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017] để hàm số $y = (m^{2} - 4) x + 2 m$ đồng biến trên ℝ.

Lời giải:

Hàm số bậc nhất y = ax + b đồng biến

$\Leftrightarrow a > 0 \Leftrightarrow m^{2} - 4 > 0 \Leftrightarrow [\begin{matrix} m > 2 \\ m < - 2 \end{matrix}$

Mà m ∈ Z mà m $\in [- 2017; 2017]$

$\Rightarrow m \in \{- 2017; - 2016; - 2015; ...; - 3\} \cup \{3; 4; 5; ...2017\}$

Vậy có 2.(2017 – 3 + 1) = 2.2015 = 4030 giá trị nguyên của m cần tìm.

Câu 31: Cho 10 chữ số 0, 1, 2, 3,..., 9. Có bao nhiêu có tự nhiên lẻ gồm 6 chữ số khác nhau, nhỏ hơn 600000 được xây dựng từ 10 số trên.

Lời giải:

Gọi số có 6 chữ số đó là $a_{1} a_{2} a_{3} a_{4} a_{5} a_{6}$

TH1: $a_{6} \in \{1; 3; 5\} \Rightarrow$ 3 cách chọn

Mà $1 \leq a_{1} \leq 5 \Rightarrow a_{1}$ có 4 cách chọn

Chọn 4 chữ số trong 8 chữ số gắn vào 4 vị trí còn lại là $A_{8}^{4}$

⇒ Số cách chọn trong TH1 là 3.4. $A_{8}^{4}$

TH2: $a_{6} \in \{7; 9\} \Rightarrow a_{6}$ có 2 cách chọn

$1 \leq a_{1} \leq 5 \Rightarrow a_{1}$ có 5 cách chọn

Chọn 4 chữ số trong 8 chữ số gắn vào 4 vị trí còn lại là $A_{8}^{4}$

⇒ Số cách chọn trong Th2 là 2.5. $A_{8}^{4}$ .

Câu 32: Một đội công nhân có 25 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 5 ngày thì cần thêm bao nhiêu người ?(mức làm của mỗi người như nhau).

Lời giải:

Tóm tắt:

9 ngày : 25 người

5 ngày : .... người

Để sửa xong quãng đường đó trong 1 ngày thì cần số người là:

25 x 9 = 225 (người)

Muốn làm xong công đó trong 5 ngày thì cần số người là:

225 : 5 = 45 (người).

Câu 33: Trung bình cộng của 2 số là 138. Biết số thứ nhất là số lẻ nhỏ nhất có 3 chữ số. Tìm số thứ 2.

Lời giải:

Tổng 2 số là: 138 x 2 = 276

Số lẻ nhỏ nhất có 3 chữ số là 101

Số thứ hai là: 276 – 101 = 175.

Câu 34: Tìm tọa độ giao điểm của đường thẳng (d) : x – 5y + 6 = 0 và trục hoành.

Lời giải:

Gọi M(x; y) là giao điểm của đường thẳng (d) và trục hoành.

Khi đó; tọa độ điểm M là nghiệm hệ phương trình:

$\{\begin{matrix} x - 5 y + 6 \\ y = 0 \end{matrix} \Rightarrow \{\begin{matrix} x = - 6 \\ y = 0 \end{matrix}$ .

Vậy tọa độ điểm M(–6; 0).

Câu 35: Hãy tính dãy số sau đây: 1 + 2 + 3 +....+ 99 ?

Lời giải:

Dãy tổng trên có số số hạng là:

(99 – 1 ) : 1 + 1 = 99 (số hạng)

Tổng của dãy tổng trên là:

(99 + 1) x 99 : 2 = 4950

Vậy 1 + 2 + 3 + ............ + 99 = 4950.

Câu 36: Tìm tập giá trị của hàm số y = 2cosx.

Lời giải:

cosx $\in [- 1; 1] \Rightarrow 2 \cos x \in [- 2; 2]$ .

Câu 37: Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB, AC theo thứ tự ở D và E.

a. Chứng minh rằng CD ⊥ AB, BE ⊥ AC.

b. Gọi K là giao điểm của BE, CD. Chứng minh AK ⊥ BC.

Lời giải:

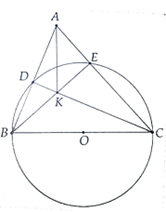
Tài liệu VietJack

a. Ta có:

$\hat{B D C} = \frac{1}{2} \overset{⏜}{B C} = \frac{1}{2} .180 ° = 90 °; \hat{B E C} = \frac{1}{2} \overset{⏜}{B C} = \frac{1}{2} .180 ° = 90 °$

$\Rightarrow \{\begin{matrix} C D ⊥ A B \\ B E ⊥ A C \end{matrix}$

b. Vì CD ⊥ AB, BE ⊥ AC nên trong ∆ABC, BE và CD là 2 đường cao

K là giao BE và CD ⇒ K là trực tâm ⇒ AK ⊥ BC.

Câu 38: Số nghiệm của phương trình sin2x – cos2x = 3sinx + cosx – 2 thuộc $(0; \frac{π}{2})$ .

Lời giải:

Với $x \in (0; \frac{π}{2}) .$ Xét PT: sin2x – cos2x = 3sinx + cosx – 2

⟺ (sin2x – cosx) + (1 – cos2x) – 3sinx + 1 = 0

⟺ (cosx + sinx –1)(2sinx – 1) = 0

$\Leftrightarrow [\begin{matrix} \sin x = \frac{1}{2} \\ \sin (x + \frac{π}{4}) = \frac{1}{\sqrt{2}} \end{matrix} \Rightarrow x = \frac{π}{3}$ do $x \in (0; \frac{π}{2})$ .

Câu 39: Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi $\vec{M P} + \vec{N P}$ bằng vectơ nào?

Lời giải:

Tài liệu VietJack

Từ M, N, P lần lượt là trung điểm các cạnh AB, AC, BC, ta suy ra MN, NP, MP là các đường trung bình của tam giác ABC.

Suy ra ANPM là hình bình hành.

Vì ANPM là hình bình hành nên theo quy tắc hình bình hành ta có:

$\vec{M P} + \vec{N P} = \vec{A N} + \vec{A M} = \vec{A P}$

Câu 40: Cho ∆MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM.

a. Chứng minh tứ giác MDEF là hình bình hành.

b. ∆MNP có điều kiện gì thì tứ giác MDEF là hình chữ nhật.

Lời giải:

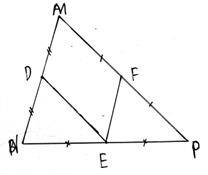
Tài liệu VietJack

a. Xét ∆MNP có: D là trung điểm MN; E là trung điểm NP (gt)

⇒ DE là đường trung bình của ∆MNP ⇒ DE // MP

Chứng minh tượng tự: EF // MN

Xét tứ giác MDEF có: MD // EF (do EF // MN); DE // MF (do DE // MP)

⇒ MDEF là hình bình hành

b. Để hình bình hành MDEF là hình chữ nhật $\Leftrightarrow \hat{F M D} = 90 °; \hat{P M N} = 90 °$

Vậy tứ giác MDEF là hình chữ nhật ⟺ ∆MNP có $\hat{N M P} = 90 °$ .

Câu 41: Cho các điểm A(1; –2), B(–2; 3), C(0; 4). Tính diện tích ∆ABC.

Lời giải:

Ta có: A(1; –2), B(–2; 3), C(0; 4)

$\Rightarrow \{\begin{matrix} \vec{A B} = (- 3; 5) \\ \vec{B C} = (2; 1) \\ \vec{C A} = (1; - 6) \end{matrix} \Rightarrow \{\begin{matrix} A B = \sqrt{{(- 3)}^{2} + 5^{2}} = \sqrt{34} \\ B C = \sqrt{2^{2} + 1^{2}} = \sqrt{5} \\ C A = \sqrt{1^{2} + {(- 6)}^{2}} = \sqrt{37} \end{matrix}$

p = $\frac{A B + B C + C A}{2} = \frac{\sqrt{34} + \sqrt{5} + \sqrt{37}}{2}$

$\Rightarrow S_{A B C} = \sqrt{p (p - A B) (p - B C) (p - C A)} = \frac{13}{2}$ .

Câu 42: Nghiệm bội lẻ là gì ?

Lời giải:

Nghiệm mũ lẻ thì người ta gọi là nghiệm bội lẻ

VD: $f (x) = {(x - 1)}^{15}$ có nghiệm x = 1 là nghiệm bội lẻ.

Câu 43: Phân tích đa thức thành nhân tử: a³ – 3a + 3b – b³.

Lời giải:

a³ – 3a + 3b – b³

= (a³ – b³) – (3a – 3b)

= (a – b)(a² + ab + b²) – 3(a – b)

= (a – b)(a² + ab + b² – 3)

Câu 44: Giải phương trình 5sin2x + 12cos2x = 13.

Lời giải:

5sin2x + 12cos2x = 13

$\Leftrightarrow \frac{5}{13} \sin 2 x + \frac{12}{13} \cos 2 x = 1$ (*)

Chọn góc a thỏa mãn $\sin a = \frac{5}{13}$ , ta có ${(\frac{5}{13})}^{2} + {(\frac{12}{13})}^{2} = 1$ nên $\cos a = \frac{12}{13}$ .

Khi đó (*) $\Leftrightarrow \sin a \sin 2 x + \cos a \cos 2 x = 1$

$\begin{array}{l} \Leftrightarrow \cos (2 x - a) = 1 \\ \Leftrightarrow 2 x - a = k 2 π (k \in ℤ) \end{array} \begin{array}{l} \Leftrightarrow 2 x = a + k 2 π (k \in ℤ) \\ \Leftrightarrow x = \frac{a}{2} + k π (k \in ℤ) \end{array}$

Vậy nghiệm của phương trình là: $x = \frac{a}{2} + k π (k \in ℤ)$ với a thỏa mãn $\sin a = \frac{5}{13}$ .

Câu 45: Giải phương trình sau: cos2x – 3sinx – 2 = 0.

Lời giải:

cos2x – 3sinx – 2 = 0

$\begin{array}{l} \Leftrightarrow 1 - 2 \sin^{2} x - 3 \sin x - 2 = 0 \\ \Leftrightarrow 2 \sin^{2} x + 3 \sin x + 1 = 0 (*) \end{array}$

Đặt t = sinx, –1 ≤ t ≤ 1

(*) $\Leftrightarrow 2 t^{2} + 3 t + 1 = 0 \Leftrightarrow [\begin{matrix} t = - 1 \\ t = - \frac{1}{2} \end{matrix} (T M)$

Với t = –1 ⟺ sinx = –1 $\Leftrightarrow x = - \frac{π}{2} + k 2 π (k \in ℤ)$

Với $t = - \frac{1}{2} \Leftrightarrow \sin x = - \frac{1}{2} \Leftrightarrow \sin x = \sin (- \frac{π}{6})$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{matrix} (k \in ℤ)$

Vậy nghiệm của phương trình: $x = - \frac{π}{2} + k 2 π; x = - \frac{π}{6} + k 2 π; x = \frac{7 π}{6} + k 2 π (k \in ℤ)$ .

Câu 46: Cho hình chữ nhật ABCD, vẽ ∆AEC vuông tại E. Chứng minh năm điểm A, B, C, D, E cùng thuộc một đường tròn.

Lời giải:

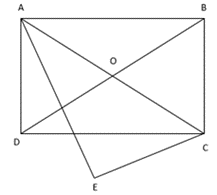
Tài liệu VietJack

Vì ABCD là hình chữ nhật nên nội tiếp đường tròn $(O; \frac{A C}{2})$

Xét tam giác AEC vuông tại E nên tam giác AEC nội tiếp đường tròn $(O; \frac{A C}{2})$ .

Vậy 5 điểm A, B, C, D, E cùng thuộc đường tròn $(O; \frac{A C}{2})$ .

Câu 47: Tìm nghiệm nguyên của phương trình: 3x + 5y = 11.

Lời giải:

Xét x = 0, suy ra $y = \frac{11}{5} \notin ℤ$ , xét y = 0, suy ra $x = \frac{11}{3} \notin ℤ$ . Do đó x, y ≠ 0.

Ta có: 3x + 5y = 11 $\Leftrightarrow y = \frac{11 - 3 x}{5} \Rightarrow 11 - 3 x \in B (5) = \{\pm 5; \pm 10; ...\}$

Đặt các số là bội của 5 có dạng 5k, k ∈ ℤ, k ≠ 0, ta có 11 – 3x = 5k, suy ra $x = \frac{11 - 5 k}{3}$ .

Vì x ∈ ℤ nên $\frac{11 - 5 k}{3} \in ℤ \Rightarrow 11 - 5 k \in B (3)$ .

Câu 48: Khoảng cách BC trong hình vẽ dưới đây bằng bao nhiêu mét, biết M và N lần lượt là trung điểm của AB và AC, MN = 5x – 18 (m); BC = 4x + 198 (m).

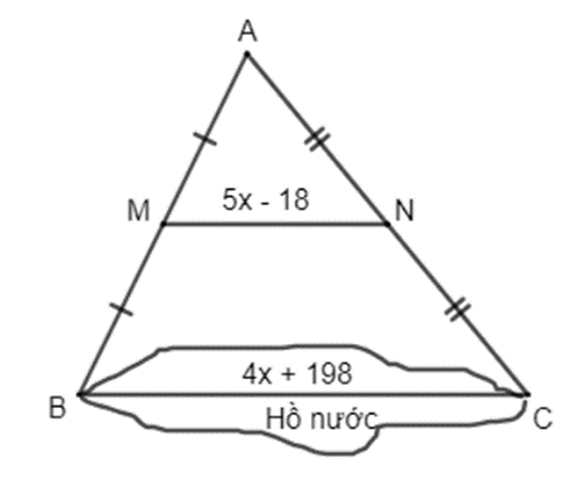
Tài liệu VietJack

Lời giải:

Xét ∆ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của ∆ABC.

Suy ra MN = $\frac{1}{2}$ BC.

Mà MN = 5x – 18 và BC = 4x + 198 nên ta có: 5x – 18 = 1212(4x + 198)

⇔ 5x – 18 = 2x + 99 ⇔ 3x = 117 ⇔ x = 39 (m).

Vậy khoảng cách BC trong hình vẽ đã cho là BC = 4.39 + 198 = 354 (m).

Câu 49: Có bao nhiêu tập con gồm 3 phần tử có chứa e, f của M = {a; b; c; d; e; f; g; h; i; j}?

Lời giải:

Các tập con cần tìm là:

$\{e; f; a\}; \{e; f; b\}; \{e; f; c\}; \{e; f; d\}; \{e; f; g\}; \{e; f; h\}; \{e; f; i\}; \{e; f; j\}$

Vậy có 8 tập con cần tìm.

Câu 50: Giải phương trình sin(2x + 1) + cos(3x – 1) = 0.

Lời giải:

sin(2x + 1) + cos(3x – 1) = 0

⟺ cos(3x – 1) = – sin(2x + 1)

⟺ cos(3x – 1) = sin(–2x – 1)

⟺ cos(3x – 1) = $\cos (\frac{π}{2} + 2 x + 1)$

$\Leftrightarrow [\begin{matrix} 3 x - 1 = \frac{π}{2} + 2 x + 1 + k 2 π \\ 3 x - 1 = - \frac{π}{2} - 2 x - 1 + k 2 π \end{matrix} (k \in ℤ) \Leftrightarrow [\begin{matrix} x = \frac{π}{2} + 2 + k 2 π \\ x = - \frac{π}{10} + \frac{k 2 π}{5} \end{matrix} (k \in ℤ)$