Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 83)

Câu 1: Một người có 66 chiếc giỏ đựng cam hoặc xoài (mỗi giỏ chỉ đựng một loại quả) được đánh số 1 đến 6. Số quả trong mỗi giỏ từ 1 đến 6 lần lượt là: 36; 39; 40; 41; 42 và 44 quả. Sau khi bán một giỏ xoài thì số cam còn lại gấp bốn lần số xoài còn lại. Hãy cho biết giỏ nào đựng cam? Giỏ nào đựng xoài?

Lời giải:

Vì số cam còn lại gấp 4 lần số xoài còn lại nên tổng số cam và xoài còn lại phải là số chia hết cho 5. Số cam và xoài mang ra chợ là:

36 + 39 + 40 + 41 + 42 + 44 = 242 (quả)

Ta có: 242 chia 5 dư 2

⇒ Giỏ xoài bán đi có số quả là số chia 5 dư 2.

Trong các số 36; 39; 40; 41; 42; 44 chỉ có số 42 chia 5 dư 2

⇒ Số cam và số xoài còn lại là: 242 – 42 = 200 (quả)

Số xoài còn lại là: 200 : 5 = 40 (quả)

Vậy các giỏ xoài là các giỏ có 40 và 42 quả.

Các giỏ cam là các giỏ có 36 quả, 39 quả, 41 quả và 44 quả.

Câu 2: Số các giá trị nguyên của tham số m để hàm số y = x³ – mx² + (m² – 2m)x có cực tiểu tại x = 0 là

A. cô số;

B. 3;

C. 2;

D. 4.

Lời giải:

Đáp án đúng là: A

Ta có: y' = 3x² – 2mx + (m² – 2m)

y' = 0 ⇔ 3x² – 2mx + (m² – 2m) = 0 (*)

Cực trị của hàm số ban đầu là nghiệm của phương trình (*):

f(x) = 3x² – 2mx + (m² – 2m) = 0

Hàm số đạt cực tiểu tại x = 0 ⇔ f ′(0) > 0

Ta có: f ′(x) = 6x – 2m

f ′(0) = −2m > 0 ⇔ m < 0

Vậy có vô số giá trị m thỏa mãn yêu cầu bài toán.

Câu 3: Trên một tấm bìa catton có ghi 4 mệnh đề sau:

(I) Trên tấm bìa này có đúng một mệnh đề sai.

(II) Trên tấm bìa này có đúng hai mệnh đề sai.

(III) Trên tấm bìa này có đúng ba mệnh đề sai.

(IV) Trên tấm bìa này có đúng bốn mệnh đề sai.

Hỏi trên tấm bìa trên có bao nhiêu mệnh đề sai?

A. 4;

B. 1;

C. 2;

D. 3;

Lời giải:

Đáp án đúng là: D

• Giả sử mệnh đề I đúng. Tức là trên tấm bìa chỉ có 1 mệnh đề I là đúng, 3 mệnh đề còn lại là sai. Tức là mệnh đề II sai.

Hay nói cách khác, trên tấm bìa phải có 2 mệnh đề đúng. Điều này mâu thuẫn với điều giả sử. Nên mệnh đề I sai.

• Giả sử mệnh đề II đúng. Tức là trên tấm bài này có 2 mệnh đề đúng và 2 mệnh đề sai. Mà theo trên thì mệnh đề I sai.

Nên hai mệnh còn lại là mệnh đề III, mệnh đề IV phải có 1 mệnh đề sai và 1 mệnh đề đúng.

Nếu mệnh đề III đúng thì mệnh đề II sai, nếu mệnh đề IV đúng thì mệnh đề II cũng sai nên mâu thuẫn với giả thiết. Hay mệnh đề II sai.

• Giả sử mệnh đề III đúng.

Nghĩa là có 3 mệnh đề sai I, II, IV. Điều này thỏa mãn vì mệnh đề I, II đã sai (theo trên), mệnh đề IV sai vì mệnh đề III đã đúng nên IV phải là mệnh đề sai.

• Giả sử mệnh đề IV đúng thì điều này mâu thuẫn với chính nó vì mệnh đề IV nói có 4 mệnh đề sai nên IV phải là mệnh đề sai.

Vậy có 3 mệnh đề sai và 1 mệnh đề đúng.

Câu 4: Có 5 bạn học sinh trong đó có hai bạn là Lan và Hồng. Có bao nhiêu cách xếp 5 học sinh trên thành một hàng dọc sao cho hai bạn Lan và Hồng đứng cạnh nhau?

A. 48;

B. 24;

C. 6;

D. 120.

Lời giải:

Đáp án đúng là: A

Số cách sắp xếp 5 học sinh trong đó có hai bạn Lan và Hồng đứng cạnh nhau là:

4!.2! = 48 (cách).

Vậy có 48 cách sắp xếp thỏa mãn yêu cầu bài toán.

Câu 5: Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?

A. 1;

B. 25;

C. 5;

D. 120.

Lời giải:

Đáp án đúng là: D

Mỗi cách xếp cho ta một hoán vị của 5 học sinh và ngược lại.

Vậy số cách xếp là P₅ = 5! = 120 (cách)

Câu 6: Cho một hình lập phương ABCDEFGH có các cạnh đều bằng nhau và bằng 7cm. Hỏi thể tích hình lập phương ABCDEFGH bằng bao nhiêu?

Lời giải:

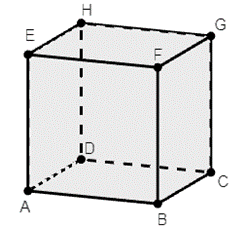
Ta có các cạnh của hình lập phương ABCD.EFGH đều bằng nhau và bằng một giá trị

a = 7cm.

Khi đó thể tích hình lập phương ABCD.EFGH là:

V = a³ = 7³ = 343 (cm³).

Câu 7: Trong các mệnh đề sau, mệnh đề nào sai?

A. Khối tứ diện là khối đa diện lồi;

B. Lắp ghép 2 khối hộp sẽ được 1 khối đa diện lồi;

C. Khối lập phương là khối đa diện lồi;

D. Khối lăng trụ tam giác là khối đa diện lồi.

Lời giải:

Đáp án đúng là: B

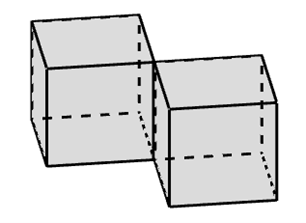
Lắp ghép 2 khối hộp chưa chắc được 1 khối đa diện lồi.

Câu 8: Trong các mệnh đề sau, mệnh đề nào sai?

A. Tồn tại tứ diện là khối tứ diện đều;

B. Tồn tại khối lăng trụ đều là khối đa diện đều;

C. Tồn tại khối hộp là khối đa diện đều;

D. Tồn tại khối chóp tứ giác đều là khối da diện đều.

Lời giải:

Đáp án đúng là: D

Không thể tồn tại khối chóp tứ giác đều là khối đa diện đều.

Câu 9: Chọn mệnh đề sai trong các mệnh đề dưới đây:

A. Tồn tại khối lăng trụ đều là khối đa diện đều;

B. Tồn tại khối chóp tứ giác đều là khối đa diện đều;

C. Tồn tại khối tứ diện là khối đa diện đều;

D. Tồn tại khối hộp là khối đa diện đều.

Lời giải:

Đáp án đúng là: B

Không thể tồn tại khối chóp tứ giác đều là khối đa diện đều.

Vậy mệnh đề sai là mệnh đề B.

Câu 10: Tìm nghiệm của phương trình 3^{x – 1} = 9.

Lời giải:

3^{x – 1} = 9

⇔ 3^{x – 1} = 3²

⇔ x – 1 = 2

⇔ x = 3

Vậy x = 3 là nghiệm của phương trình.

Câu 11: Tập nghiệm của bất phương trình ln(1 – x) < 0:

A. (−∞; 1);

B. (0; 1);

C. (0; +∞);

D. (−∞; 0).

Lời giải:

Đáp án đúng là: B

Ta có: ln(1 – x) < 0

⇔ 0 < 1 – x < e⁰

⇔ 0 < x < 1

Vậy tập nghiệm của bất phương trình là (0; 1)

Câu 12: Cho hai đường tròn bằng nhau (O; R) và (O’; R’) phân biệt. Có bao nhiêu phép vị tự biến (O; R) thành (O’; R’)?

A. 0;

B. 1;

C. 2;

D. Vô số.

Lời giải:

Đáp án đúng là: B

Vì O và O’ riêng biệt, R = R’

Suy ra chỉ có duy nhất 1 phép vị tự biến (O; R) thành (O’; R’).

Câu 13: Chứng minh rằng với mọi số nguyên dương n ta luôn có n³ + 5n chia hết cho 6.

Lời giải:

Ta có: n³ + 5n = n³ – n + 6n = n(n² – 1) + 6n

= n(n – 1)(n + 1) + 6n

Vì n là số nguyên dương nên suy ra:

Tích của ba số nguyên dương liên tiếp: n – 1; n; n + 1 chia hết cho 2 và 3

Nên n.(n – 1)(n + 1) chia hết cho 6.

Mà 6n chia hết cho 6 nên suy ra:

n(n – 1)(n + 1) + 6n chia hết cho 6.

Suy ra với mọi số nguyên dương ta luôn có n³ + 5n chia hết cho 6 (đpcm)

Câu 14: Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (A) 4x – 3y – 7z + 3 = 0 và điểm I(1; −1; 2). Phương trình mặt phẳng đối xứng với (A) qua I là

A. (B): 4x – 3y – 7z – 3 = 0;

B. (B): 4x – 3y – 7z + 11 = 0;

C. (B): 4x – 3y – 7z – 11 = 0;

D. (B): 4x – 3y – 7z + 5 = 0.

Lời giải:

Đáp án đúng là: B

Do (B) đối xứng với (A) qua O nên (B) // (A)

Suy ra (B): 4x – 3y – 7z + D = 0 với D ≠ 3.

Chọn M(0; 1; 0) ∈ (A)

Suy ra tọa độ điểm N đối xứng với M qua I là: N(2; −3; 2) ∈ (B)

Thay toạn độ điểm N vào phương trình (B) ta được: D = 11

Vậy phương trình mặt phẳng (B) là: 4x – 3y – 7z + 11 = 0.

Câu 15: Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4 cm.

Lời giải:

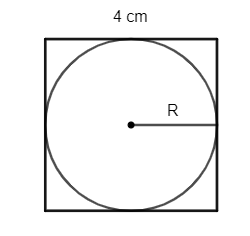
Hình tròn nội tiếp hình vuông có cạnh 4 cm thì có R = 2 cm.

Vậy diện tích hình tròn là: pR² = 4p (cm²)

Câu 16: Phân tích đa thức thành nhân tử:

a) x² – 4x + 4;

b) x³ + 9x² + 27x + 27.

Lời giải:

a) x² – 4x + 4 = x² – 2.x.2 + 2² = (x – 2)².

b) x³ + 9x² + 27x + 27 = x³ + 3.x² . 3 + 3.x.3² + 3³ = (x + 3)³.

Câu 17: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q) : 2x – y + 5z – 15 = 0 và điểm E(1, 2, -3). Tìm phương trình mặt phẳng (P) qua E và song song với (Q).

Lời giải:

Mặt phẳng (P) đi qua E(1, 2, -3) và nhận n_Q = (2, -1, 5) là một vectơ pháp tuyến

⇒ (P) : 2(x – 1) – (y – 2) + 5(z + 3) = 0

⇔ 2x – y + 5z + 15 = 0.

Vậy phương trình mặt phẳng (P) là 2x – y + 5z + 15 = 0.

Câu 18: Tìm giá trị lớn nhất của hàm số y = 1 – 2cos x – cos²x.

Lời giải:

Ta có: y = 1 – 2cos x – cos²x = 2 – (cos x + 1)²

Ta thấy: -1 ≤ cos x ≤ 1 ⇔ 0 ≤ cos x + 1 ≤ 2

⇒ 0 ≤ (cos x + 1)² ≤ 4

Do đó y = 2 – (cos x + 1)² ≤ 2 – 0 = 2.

Vậy giá trị lớn nhất của hàm số là 2.

Câu 19: Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AD. Gọi G là trọng tâm tam giác SCD. Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (ABG) là:

A. Một tam giác.

B. Một tứ giác.

C. Một ngũ giác.

D. Một lục giác.

Lời giải:

Đáp án đúng là: B

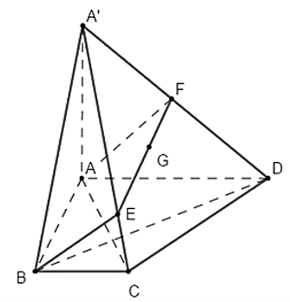
Từ G kẻ đường thẳng song song với AB lần lượt cắt SC, SD tại E, F.

Vậy thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (ABG) là hình tứ giác ABEF.

Câu 20: Tìm tất cả các giá trị của tham số m để phương trình x⁴ – 10x² + m = 0 có 4 nghiệm phân biệt lập thành một cấp số cộng.

Lời giải:

Ta có phương trình đã cho có 4 nghiệm phân biệt lập thành một cấp số cộng thì điều kiện cần là 9b² = 100ac hay 9.10² = 100.1.m ⇔m=9.

Với m = 9 thì phương trình đã cho trở thành x⁴ − 10x² + 9 = 0 ⇔ x = ±1; x = ±3.

Bốn số −3; −1; 1; 3 lập thành một cấp số cộng nên m = 9 là giá trị cần tìm.

Câu 21: Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số là

A. 0,001.

B. 0,002.

C. 0,003.

D. 0,004.

Lời giải:

Đáp án đúng là: A

Ta có: π = 3,141592654... nên sai số tuyệt đối của 3,14 là:

∆ = |3,14 – π| < |3,14 – 3,141| = 0,001.

Câu 22: Một hộp đựng 8 viên bi đỏ được đánh số từ 1 đến 8, 6 viên bi xanh được đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn 2 viên bi từ hộp đó sao cho 2 viên bi khác màu và khác số.

Lời giải:

Bước 1: Chọn một viên bi xanh có 6 cách chọn.

Bước 2: Chọn một viên bi đỏ, được đánh số khác với viên bi xanh nên có 7 cách chọn.

Theo quy tắc nhân có 6.7 = 42 (cách chọn).

Câu 23: Hình nào sau đây không có tâm đối xứng?

A. Hình vuông;

B. Hình tròn;

C. Hình tam giác đều;

D. Hình thoi.

Lời giải:

Đáp án đúng là: C

Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.

Hình tròn có tâm đối xứng là tâm của nó.

Hình thoi có tâm đối xứng là giao điểm của hai đường chéo.

Tam giác đều không có tâm đối xứng.

Câu 24: Hình nào sau đây không có tâm đối xứng?

A. Hình thoi;

B. Hình hình bình hành;

C. Hình thang cân;

D. Hình chữ nhật.

Lời giải:

Đáp án đúng là: C

- Hình chữ nhật có hai trục đối xứng là đường nối hai trung điểm của hai cạnh đối diện và tâm đối xứng là giao của hai đường chéo.

- Hình thang không có trục đối xứng, cũng ko có tâm đối xứng.

- Hình hình hành không có trục đối xứng và có tâm đối xứng là giao điểm của hai đường chéo.

- Hình thoi là hình có hai trục đối xứng là hai đường chéo và tâm đối xứng là giao điểm của hai đường chéo.

Vậy hình không có tâm đối xứng là hình thang cân.

Câu 25: Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây là đúng?

A. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≥ 0 ∀x ∈ (a; b) và f ′(x) = 0 tại hữu hạn giá trị x ∈ (a; b);

B. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) < 0 ∀x ∈ (a; b);

C. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≤ 0 ∀x ∈ (a; b);

D. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≥ 0 ∀x ∈ (a; b);

Lời giải:

Đáp án đúng là: A

Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≥ 0 ∀x ∈ (a; b) và f ′(x) = 0 tại hữu hạn giá trị x ∈ (a; b).

Câu 26: Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?

A. Nếu f ′(x) < 0 với mọi x ∈ (a; b) thì hàm số y = f (x) nghịch biến trên (a; b);

B. Nếu f ′(x) > 0 với mọi x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b);

C. Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ′(x) ≤ 0 với mọi x ∈ (a; b);

D. Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ′(x) > 0 với mọi x ∈ (a; b).

Lời giải:

Đáp án đúng là: D

+) Nếu f ′(x) < 0 với mọi x ∈ (a; b) thì hàm số y = f (x) nghịch biến trên (a; b)

+) Nếu f ′(x) > 0 với mọi x ∈ (a; b) thì hàm số y = f (x) đồng biến trên (a; b)

+) Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ′(x) ≤ 0 với mọi x ∈ (a; b) và f ′(x) = 0 tại hữu hạn giá trị x ∈ (a; b)

+) Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ′(x) ≥ 0 với mọi x ∈ (a; b) và f ′(x) = 0 tại hữu hạn giá trị x ∈ (a; b).

Câu 27: Hình trụ có bán kính đáy bằng a và thiết diện qua trục là một hình vuông. Tính thể tích khối trụ đó.

Lời giải:

Do thiết diện tạo thành là một hình vuông nên độ dài đường cao h của hình trụ bằng 2 bán kính r của đáy.

Do đó h = 2r = 2a.

Khi đó thể tích hình trụ là:

V = pr²h = p.a².(2a) = 2pa³.

Câu 28: Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính theo a diện tích xung quanh của hình trụ.

Lời giải:

Do thiết diện tạo thành là một hình vuông nên độ dài đường cao h của hình trụ bằng 2 bán kính r của đáy.

Do đó h = 2r = 2a.

Khi đó diện tích xung quanh của hình trụ là:

S_xq = 2prh = 2p.a.(2a) = 4pa².

Câu 29: Cho khối trụ tròn xoay có diện tích toàn phần gấp 2 lần diện tích xung quanh và có bán kính đáy bằng 6 cm. Tính thể tích khối trụ đó.

Lời giải:

Vì diện tích toàn phần của khối trụ gấp 2 lần diện tích xung quanh của nó nên:

2prh + 2pr² = 2.2prh

⇔ 2pr² = 2prh

⇔ r = h

⇒ h = 6 cm

Vậy thể tích của khối trụ tròn xoay là:

V = pr²h = p.6².6 = 216p.

Câu 30: Cho hình nón có bán kính đáy bằng 5. Biết rằng khi cắt hình nón cho bởi mặt phẳng qua trục, thiết diện thu được là một tam giác đều. Diện tích toàn phần của hình nón đã cho bằng:

Lời giải:

Do thiết diện qua trục là tam giác đều suy ra:

l = 2r = 2.5 = 10

Diện tích toàn phần của hình nón là:

S_tp = prl + pr² = p.5.10 + p.5² = 75p.

Câu 31: Lãi suất gửi tiết kiệm của ngân hàng A thời gian vừa qua thay đổi liên tục. Bạn Duy gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,8% một tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2% một tháng trong nửa năm tiếp theo. Và bạn Duy tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 1% một tháng. Đồng thời bạn Duy quyết định gửi thêm một số tháng tròn nữa. Biết rằng khi rút tiền bạn Duy được cả vốn lẫn lãi là 12 153 337,95 triệu đồng. Tổng số tháng mà bạn Duy gửi tiết kiệm là:

Lời giải:

Gọi x là số tháng gửi với lãi suất 0,8% một tháng (0 < x < 12)

Gọi y là số tháng gửi với lãi suất 1% một tháng

Tổng số tháng mà bạn Duy gửi tiết kiệm là x + 6 + y tháng

Theo giá thiết, ta có:

10.10⁶.(1 + 0,8%)^x.(1 + 1,2%)⁶.(1 + 1%)^y = 12153337,95

⇔ 1,008^x.1,01^y = 1,131

Lần lượt gán các giá trị của x bằng 1 đến 11 với x là số nguyên ta sẽ tìm được y nguyên khi x = 8, y = 6.

Suy ra tổng số tháng mà bạn Duy gửi tiết kiệm là:

x + 6 + y = 8 + 6 + 6 = 20 tháng.

Câu 32: Lãi suất gửi tiền tiết kiệm của các ngân hàng trong thời qua liên tục thay đổi. Bác Mạnh gửi vào một số ngân hàng số tiền 5 triệu đồng với lãi suất 0,7%/ tháng. Sau sáu tháng gửi tiền, lãi suất tăng lên 0,9%/ tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6%/ tháng và giữ ổn định. Biết rằng nếu bác Mạnh không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (ta gọi đó là lãi kép). Sau một năm gửi tiền, bác Mạnh rút được số tiền là bao nhiêu? (biết trong khoảng thời gian này bác Mạnh không rút tiền ra).

Lời giải:

Sau 6 tháng gửi tiền, bác Mạnh có:

T₁ = 5.(1 + 0,7%)⁶ (triệu đồng)

Số tiền bác Mạnh nhận được khi gửi tiền đến tháng thứ 10 là:

T₂ = T₁.(1 + 0,9%)³ (triệu đồng)

Vậy sau 1 năm, số tiền bác Mạnh nhận được là:

T = T₂.(1 + 0,6%)³ = 5 452 733,453 (đồng).

Câu 33: Từ các chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho hai chữ số 1 và 2 luôn đứng cạnh nhau?

Lời giải:

Xếp số 1 và 2 cạnh nhau có 2! = 2 (cách)

Coi cặp số 12 như một số, kết hợp với 3 số còn lại được 4 số, hoán vị chúng có:

4! = 24 (cách)

Mà 1 và 2 có thể đổi chỗ cho nhau nên vậy có:

2.24 = 48 số thỏa mãn.

Câu 34: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Tính số cách xếp sao cho các nữ sinh luôn ngồi cạnh nhau.

Lời giải:

Ta coi 4 nữ sinh là một nhóm, xếp nhóm 4 bọn nữ và 6 bạn nam vào 10 chỗ ngồi là số hoán vị của 7 phần tử.

Trong 4 nữ sinh còn có thể hoán đổi vị trí nên ta có:

7!.4! = 12 0960 cách xếp thỏa mãn yêu cầu.

Câu 35: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau và các nam sinh luôn ngồi cạnh nhau?

Lời giải:

Xếp 6 học sinh nam ngồi cạnh nhau có số cách là 6! = 720 (cách).

Xếp 4 học sinh nữ ngồi cạnh nhau có số cách là 4! = 24 (cách).

Nam và nữ có thể đổi chỗ cho nhau nên có 2 trường hợp.

Vậy số cách xếp thỏa mãn yêu cầu bài toán là 2.720.24 = 34 560 (cách).

Câu 36: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước;

B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước;

C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước;

D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Lời giải:

Đáp án đúng là: D

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước là mệnh đề đúng.

Câu 37: Cho hàm số y = x³ – 3x² + 6x + 5. Tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất có phương trình là

A. y = 3x + 9;

B. y = 3x + 3;

C. y = 3x + 12.

D. y = 3x + 6.

Lời giải:

Đáp án đúng là: D

Gọi M(a; b) là điểm thuộc đồ thị hàm số có tiếp tuyến thỏa mãn.

y’ = 3x² – 6x + 6

⇒ y’(a) = 3a² – 6a + 6 = 3(a – 1)² + 3

⇒ min y’(a) = 3 ⇔ a = 1

Suy ra y(1) = 9

Do đó phương trình tiếp tuyến tại M(1; 9) là y = 3(x – 1) + 9y = 3x + 6.

Vậy phương trình tiếp tuyến cần tìm là y = 3x + 6.

Câu 38: Một miếng bìa hình chữ nhật có chu vi 72 cm. Người ta cắt bỏ đi 4 hình vuông bằng nhau ở 4 góc.

a) Tìm chu vi miếng bìa còn lại.

b) Nếu phần chiều dài còn lại của miếng bìa hơn phần còn lại của chiều rộng miếng bìa là 12 cm thì độ dài các cạnh của miếng bìa hình chữ nhật ban đầu là bao nhiêu?

Lời giải:

a) Ta thấy rằng tại mỗi góc bị cắt thì chu vi của hình chữ nhật bằng tổng 2 cạnh của mỗi hình vuông.

Sau khi cắt thì tại mỗi góc thì chu vi của hình chữ nhật vẫn bằng tổng 2 cạnh còn lại của mỗi hình vuông.

Mà hình vuông có 4 cạnh bằng nhau nên chu vi của hình chữ nhật không đổi và bằng 72 cm.

b) Tổng chiều dài và chiều rộng: 72 : 2 = 36 (cm)

Vì Phần còn lại của chiều dài hơn phần còn lại của chiều rộng 12 cm nên chiều dài hơn chiều rộng 12 cm

Chiều dài ban đầu: (36 + 12) : 2 = 24 (cm)

Chiều rộng ban đầu: 36 − 24 = 12 (cm)

Đáp số: a) 72 cm.

b) Chiều dài: 24 cm; chiều rộng: 12 cm.

Câu 39: Chu vi một miếng bìa hình chữ nhật bằng 84 cm. Người ta cắt bỏ đi 4 hình vuông bằng nhau ở bốn góc.

a) Tìm chu vi miếng bìa còn lại.

b) Nếu chiều rộng của miếng bìa còn lại kém chiều dài là 12 cm thì độ dài các cạnh của miếng bìa hình chữ nhật ban đầu là bao nhiêu?

Lời giải:

a) Ta thấy rằng tại mỗi góc bị cắt thì chu vi của hình chữ nhật bằng tổng 2 cạnh của mỗi hình vuông.

Sau khi cắt thì tại mỗi góc thì chu vi của hình chữ nhật vẫn bằng tổng 2 cạnh còn lại của mỗi hình vuông.

Mà hình vuông có 4 cạnh bằng nhau nên chu vi của hình chữ nhật không đổi và bằng 84 cm.

b) Nửa chu vi miếng đất hình chữ nhật là: 84 : 2 = 42 (cm)

Vì phần còn lại của chiều dài hơn phần còn lại của chiều rộng 12 cm nên chiều dài hơn chiều rộng 12 cm

Chiều dài ban đầu: (42 + 12) : 2 = 27 (cm)

Chiều rộng ban đầu: 42 − 27 = 15 (cm)

Đáp số: a) 84 cm

b) Chiều dài: 27 cm; chiều rộng: 15 cm

Câu 40: Một trường tổ chức cho khoảng từ 700 đến 800 học sinh đi tham quan bằng ô tô. Tính số học sinh đi tham quan, biết rằng nếu xếp 40 học sinh hay 45 học sinh vào một xe thì vừa đủ.

Lời giải:

Gọi a (học sinh) là số học sinh của trường đó.

Vì a chia hết cho cả 40 và 45 nên a ∈ BC(40, 45).

Ta có 40 = 2³ . 5; 45 = 3² . 5

⇒ BCNN(40, 45) = 2³ . 3² . 5 = 360

⇒ a ∈ BC(40, 45) = B(360) = {0; 360; 720; 1080; ...}.

mà 700 ≤ a ≤ 800 nên a = 720.

Vậy số học sinh là 720 học sinh.

Câu 41: Một tổ có 6 học sinh, trong đó có 3 học sinh nam và 3 học sinh nữ. Hỏi có bao nhiêu cách xếp các học sinh trong tổ thành một hàng dọc sao cho nam, nữ đứng xen kẽ nhau?

A. 36;

B. 42;

C. 102;

D. 72.

Lời giải:

Đáp án đúng là: D

Ta xét hai trường hợp:

• TH1. Bạn nam đứng đầu hàng, khi đó số cách sắp xếp là 3.2.3! = 36 (cách).

• TH2. Bạn nữ đứng đầu hàng, tương tự TH1, suy ra có 36 cách sắp xếp.

Vậy có 72 cách sắp xếp thỏa mãn yêu cầu bài toán.

Câu 42: Hai bể nước có dung tích bằng nhau. Cùng 1 lúc người ta cho 2 vòi nước chảy vào 2 bể. Vòi thứ nhất mỗi giờ chảy được 50 lít nước. Vòi thứ 2 mỗi giờ chảy được 30 lít nước. Sau khi bể thứ nhất đầy nước thì bể thứ 2 phải chảy thêm 600 lít nữa mới đầy. Hỏi dung tích của bể là bao nhiêu lít nước?

Lời giải:

Hai vòi chênh lệch nhau về độ chảy là:

50 – 30 = 20 (lít)

Vòi thứ nhất chảy trong bể mất số thời gian là:

600 : 20 = 30 (phút)

Dung tích của bể là:

50 × 30 = 1500 (lít)

Đáp số: 1500 lít nước

Câu 43: Các thành phố A, B, C được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ thành phố A đến thành phố C mà qua thành phố B chỉ một lần?

A. 8;

B. 12;

C. 6;

D. 4.

Lời giải:

Đáp án đúng là: A

Có số cách là: 4.2 = 8 (cách).

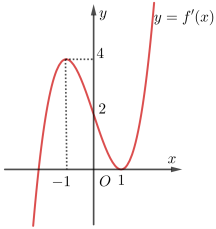
Câu 44: Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ. Đồ thị hàm số y = f ‘(x) như hình vẽ sau:

Số điểm cực trị của hàm số y = f (x) − 4x là:

Lời giải:

Đặt: g (x) = f (x) − 4x

Ta có: g’(x) = f ‘(x) − 4 = 0 ⇔ f ‘(x) = 4

Dựa vào đồ thị, suy ra phương trình f ‘(x) = 4 có 2 nghiệm x₁; x₂ trong đó x₁ = −1 là nghiệm kép và x₂ > 1 là nghiệm đơn.

Suy ra phương trình g’(x) = 0 có 2 nghiệm x₁; x₂ nhưng g’(x) đổi dấu duy nhất 1 lần khi qua nghiệm x₂ này.

Vậy hàm số y = f (x) − 4x có một điểm cực trị.

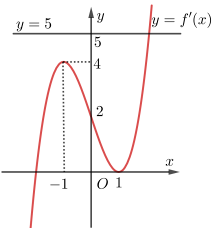
Câu 45: Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ. Đồ thị hàm số y = f ‘(x) như hình vẽ sau:

Số điểm cực trị của hàm số y = f (x) − 5x là:

Lời giải:

Ta có y = f (x) − 5x

Suy ra y’ = f ‘(x) − 5 = 0 ⇔ f ‘(x) = 5

Số điểm cực trị của hàm số y = f (x) − 5x là số nghiệm bội lẻ của phương trình y’ = 0.
Dựa vào đồ thị ta có y = f ‘(x) cắt đường thẳng y = 5 tại duy nhất một điểm.

Suy ra số điểm cực trị của hàm số y = f (x) − 5x là 1.

Câu 46: Tìm tất cả các giá trị của tham số m để phương trình cos² x = m − 1 có nghiệm.

Lời giải:

Ta có: −1 ≤ cos x ≤ 1 ⇒ 0 ≤ cos² x ≤ 1

Nên để phương trình cos² x = m − 1 có nghiệm thì:

0 ≤ m − 1 ≤ 1 ⇔ 1 ≤ m ≤ 2

Vậy 1 ≤ m ≤ 2 là các giá trị cần tìm của tham số m.

Câu 47: Tìm tất cả các giá trị của tham số m để phương trình cos 2x = m có nghiệm.

Lời giải:

Ta có: −1 ≤ cos 2x ≤ 1

Nên để phương trình cos 2x = m có nghiệm thì: −1 ≤ m ≤ 1

Vậy −1 ≤ m ≤ 1 là các giá trị cần tìm của tham số m.

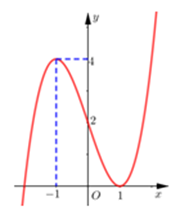
Câu 48: Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ dưới đây. Tìm số nghiệm của phương trình f(x) = 3.

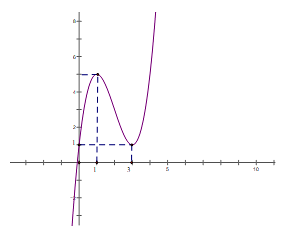
Lời giải:

Dựa vào hình vẽ ta thấy đường thẳng y = 3 cắt đồ thị hàm số tại 3 điểm.

Vậy phương trình f(x) = 3 có 3 nghiệm phân biệt.

Câu 49: Chứng minh hai góc kề nhau của một hình bình hành không thể có số đo là 40° và 50°.

Lời giải:

Trong hình bình hành có các góc đối nhau và tổng các góc trong hình bình hành phải bằng 360°

Mặt khác ta có: 40° . 2 + 50° . 2 = 180° ≠ 360°.

Vậy hai góc kề của hình bình hành không thể có số đo 40° và 50°.

Câu 50: Điều kiện để hàm số bậc ba không có cực trị là phương trình y’ = 0 có:

A. nghiệm kép.

B. vô nghiệm.

C. hai nghiệm phân biệt.

D. Cả A và B đúng.

Lời giải:

Đáp án đúng là: D

Điều kiện để hàm số bậc ba không có cực trị là phương trình y' = 0 có nghiệm kép hoặc vô nghiệm.