Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 6)

Bài 24: Từ một điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC với (O; R) (B và C là 2 tiếp điểm).

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn và AO ⊥ BC tại H.

b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC tại E. Chứng minh: DC // OA và CD . CO = BA . CE.

Lời giải:

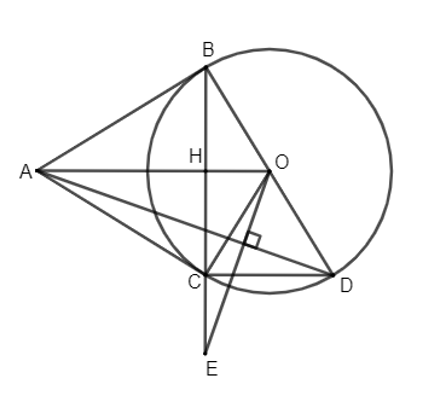
a) Vì AB, AC là hai tiếp tuyến cắt nhau tại A của đường tròn (O; R) nên \(\widehat {ABO} = \widehat {ACO} = 90^\circ \).

Xét tứ giác ABOC có $\widehat{ABO}+\widehat{ACO}=90°+90°=180°$.

Suy ra tứ giác ABOC là tứ giác nội tiếp.

Vậy bốn điểm A, B, O, C cùng thuộc một đường tròn.

Lại có theo tính chất của hai tiếp tuyến cắt nhau AC và AB, suy ra AO là đường trung trực của BC nên AO ⊥ BC tại H.

b) Vì AO ⊥ BC tại H và AO là đường trung trực của BC nên H là trung điểm của BC.

Mà O là trung điểm của BD (đường kính BD trong đường tròn tâm O).

Do đó, OH là đường trung bình của tam giác BCD.

Suy ra OH // CD nên OA // CD.