Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 95)

Đề bài. Cho (O) và A là điểm nằm ngoài (O). Qua A vẽ tiếp tuyến AB, AC với (O) với B,C là tiếp điểm. OA cắt BC tại DA

a) Chứng minh OA là đường trung trực BC.

b) Chứng minh OD.DA = BD²

c) Vẽ đường kính BE, AE cắt (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh OD.OA = OG.OH

d) Chứng minh EH là tiếp tuyến của (O)

Lời giải:

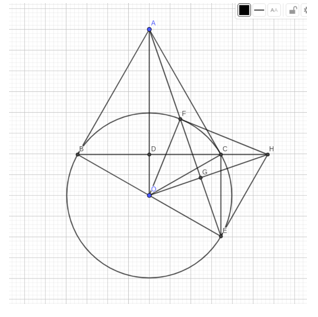a) Ta có: AB, AC là tiếp tuyến của (O) nên AB = AC

Mà OB = OC = R

Nên AO là trung trực BC

b) AB ⊥ OB, BD ⊥ OA nên OB² = OD.OA

BD² = OD.DA (hệ thức lượng trong tam giác ABO vuông tại B, BD là đường cao)

c) Xét tam giác OAG và tam giác OHD có:

Chung $\widehat{O}$

$\widehat{OGA}=\widehat{HDO}={90}^{\circ }$

⇒ ΔOAG ∼ ΔOHD (g.g)
⇒ $\frac{OA}{OH}=\frac{OG}{OD}$ hay OA.OD = OH.OG

d) Ta có: OA.OD = OH.OG = OB² = OE²

Suy ra: $\frac{OE}{OH}=\frac{OG}{OE}$

⇒ ΔOGE ∼ ΔOEH (c.g.c)

Nên: $\widehat{OEH}=\widehat{OGE}={90}^{\circ }$

Vậy EH là tiếp tuyến của (O).