Công thức tính thể tích Khối tròn xoay và bài tập vận dụng

diep4602 Ngày: 26-05-2023 Tổng hợp kiến thức

1.1 K

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Công thức tính thể tích Khối tròn xoay và bài tập vận dụng, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Công thức tính thể tích Khối tròn xoay và bài tập vận dụng

1. Định nghĩa thể tích Khối tròn xoay

Khi ta quay một mặt phẳng quanh trục cố định ta được một khối gọi là khối tròn xoay. Trong quá trình học tại trường trung học phổ thông, các bạn sẽ được làm quen với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay...

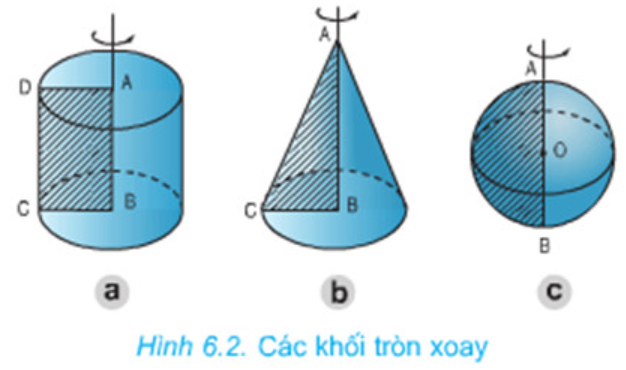
Công thức tính thể tích Khối tròn xoay và bài tập vận dụng (ảnh 1)

2. Công thức tính thể tích Khối tròn xoay

* Quay quanh trục Ox:

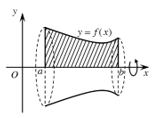
Hình giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b (trong đó f(x) liên tục trên đoạn [a;b]) quay quanh trục Ox, ta được khối tròn xoay.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} {[f (x)]}^{2} d x$

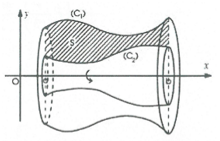
Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

Hình giới hạn bởi hai đường cong y = f(x), y = g(x) và hai đường thẳng x = a, x = b (trong đó f(x), g(x) liên tục trên đoạn [a;b]) quay quanh trục Ox.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} |f^{2} (x) - g^{2} (x)| d x$

Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

* Quay quanh trục Oy:

Hình giới hạn bởi đường cong x = f(y), trục Oy và hai đường thẳng y = c; y = d (trong đó f(x) liên tục trên đoạn [c; d]) quay quanh trục Oy, ta được khối tròn xoay.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} {[f (y)]}^{2} d y$

3. Bài tập vận dụng

Bài 1: Tính thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi các đường y = sin x, trục hoành, hai đường thẳng $x = 0; x = \frac{π}{4}$ quay quanh trục hoành?

Lời giải

Hình phẳng giới hạn bởi các đường $y = \sin x; y = 0; x = 0; x = \frac{π}{4}$ quay quanh trục Ox nên có thể tích:

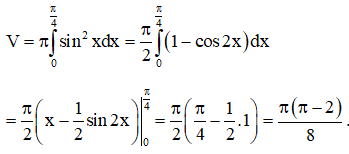
Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

Bài 2: Cho hình phẳng H giới hạn bởi các đường: $y = x; y = \sqrt{x}$ . Tính thể tích khối tròn xoay được tạo thành khi quay H quanh trục hoành?

Lời giải

Phương trình hoành độ giao điểm của hai đường:

$x = \sqrt{x} \Rightarrow [\begin{array}{l} x = 0 \\ x = 1 \end{array}$

Thể tích khối tròn xoay được tạo bởi hai đường $y = x; y = \sqrt{x}$ là:

$V = π \int_{0}^{1} |x^{2} - {(\sqrt{x})}^{2}| d x = π \int_{0}^{1} |x^{2} - x| d x = π {|\frac{x^{3}}{3} - \frac{x^{2}}{2}||}_{0}^{1} = π |\frac{1}{3} - \frac{1}{2}| = \frac{π}{6}$

Bài 3: Tính thể tích của khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng x=0, x=π (hình vẽ) quanh trục Ox.

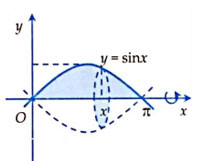
Công thức tính thể tích Khối tròn xoay và bài tập vận dụng (ảnh 1)

Lời giải

Áp dụng công thức ở định lý trên ta có

$V=\pi \int_0^\pi \sin ^2 x d x=\frac{\pi}{2} \int_0^\pi(1-\cos 2 x) d x$

$=\left.\frac{\pi}{2}\left(x-\frac{1}{2} \sin 2 x\right)\right|_0 ^\pi$

$=\frac{\pi}{2}\left(\pi-\frac{1}{2} \sin 2 \pi\right)-\frac{\pi}{2}\left(0-\frac{1}{2} \sin 0\right)$

$=\frac{\pi^2}{2}$

Bài 4: Tính thể tích khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong $y=\sqrt{A^2-x^2}$ và trục hoành quanh trục hoành.

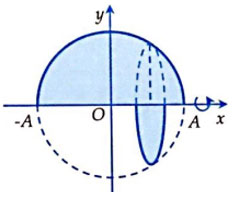
Công thức tính thể tích Khối tròn xoay và bài tập vận dụng (ảnh 3)

Lời giải

Ta thấy:

$y=\sqrt{A^2-x^2}<=>\ y^2=A^2\ -x^2\ \ <=>\ y^2\ +x^2\ =\ A^2$

Do $\sqrt{A^2-x^2}\ge\ 0$ với mọi x, do vậy đây là phương trình nửa đường tròn tâm O, bán kính R = A nằm phía trên trục Ox. Khi quay quanh trục Ox thì hình phẳng sẽ tạo nên một khối cầu tâm O, bán kính R = A (hình vẽ). Do vậy ta có luôn

$V=\frac{4}{3}\pi A^3$

Vậy với bài toán dạng này, ta không cần viết công thức tích phân mà kết luận luôn theo công thức tính thể tích khối cầu.

Bài 5: Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 1, biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x(0≤x≤1) là một hình chữ nhật có độ dài hai cạnh là x và ln(x²+1).

Lời giải

Do thiết diện là hình chữ nhật nên diện tích thiết diện là:

$S(x)=x\ln(x2^{ }+1)$

Ta có thể tích cần tính là

$\mathrm{V}=\int_0^1 \mathrm{x} \ln \left(\mathrm{x}^2+1\right) \mathrm{dx}$

$\mathrm{V}=\frac{1}{2} \int_0^1 \ln \left(\mathrm{x}^2+1\right) \mathrm{d}\left(\mathrm{x}^2+1\right)$

$=\left.\frac{1}{2}\left(\mathrm{x}^2+1\right) \ln \left(\mathrm{x}^2+1\right)\right|_0 ^1-\frac{1}{2} \int_0^1\left(\mathrm{x}^2+1\right) \mathrm{d}\left(\ln \left(\mathrm{x}^2+1\right)\right)$

$=\ln 2-\frac{1}{2} \int_0^1 2 x d x=\ln 2-\frac{1}{2}$

Bài 6: Cho hình phẳng giới hạn bởi các đường y = 3x; y = x; x = 0; x = 1 quay xung quanh trục Ox. Tính thể tích của khối tròn xoay tạo thành.

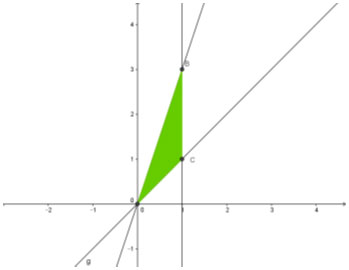
Công thức tính thể tích Khối tròn xoay và bài tập vận dụng (ảnh 4)

Lời giải

Tọa độ giao điểm của đường x = 1 với y = x và y = 3x là các điểm C(1;1) và B(3;1). Tọa độ giao điểm của đường y = 3x với y = x là O(0;0).

Vậy thể tích của khối tròn xoay cần tính là:

$V=\pi \int_0^1\left|9 x^2-x^2\right| d x=\pi \int_0^1 8 x^2 d x$

$\Leftrightarrow V=\left.\pi \frac{8 x^3}{3}\right|_0 ^1=\frac{8}{3} \pi$

Bài 7: Cho hình phẳng giới hạn bởi các đường y = 2x²; y² = 4x quay xung quanh trục Ox. Tính thể tích của khối tròn xoay tạo thành.

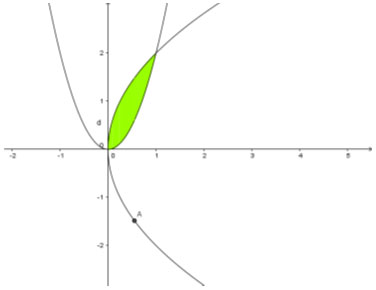
Công thức tính thể tích Khối tròn xoay và bài tập vận dụng (ảnh 5)

Lời giải

Với $x\in[0;2]$ thì $y^2=4x$ tương đương $y=2\sqrt{x}$ . Tọa độ giao điểm của đường $\mathrm{y}=2 \mathrm{x}^2$ với $\mathrm{y}^2=4 \mathrm{x}$ là các điểm O(0;0) và A(1;2).