Đạo hàm là gì? Các quy tắc tính đạo hàm, Ý nghĩa của đạo hàm

Van Anh Ngày: 21-11-2024 Tổng hợp kiến thức

160

Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Đạo hàm là gì? Các quy tắc tính đạo hàm, Ý nghĩa của đạo hàm, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Đạo hàm, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Đạo hàm là gì? Các quy tắc tính đạo hàm, Ý nghĩa của đạo hàm

A. Lý thuyết Đạo hàm

1. Định nghĩa

Cho hàm số $y = f (x)$ xác định trên khoảng $(a; b)$ , $x_{0} \in (a; b)$ . Giới hạn hữu hạn (nếu có) của tỉ số $\frac{f (x) - f (x_{0})}{x - x_{0}}$ khi $x \to x_{0}$ được gọi là đạo hàm của hàm số đã cho tại $x_{0}$ , kí hiệu là $f^{'} (x_{0})$ hay $y^{'} (x_{0})$ . Như vậy:

$f^{'} (x_{0}) = lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}}$

Nếu đặt $x - x_{0} = ∆ x$ và $∆ y = f (x_{0} + ∆ x) - f (x_{0})$ thì ta có

$f^{'} (x_{0}) = lim_{Δ x \to 0} \frac{Δ y}{Δ x}$

Đại lượng $∆ x$ được gọi là số gia của đối số tại $x_{0}$ và đại lượng $∆ y$ được gọi là số gia tương ứng của hàm số.

2. Quy tắc tính đạo hàm bằng định nghĩa

Bước 1. Với $∆ x$ là số gia của số đối tại $x_{0}$ ,tính $∆ y = f (x_{0} + ∆ x) - f (x_{0})$ ;

Bước 2. Lập tỉ số $\frac{Δ y}{Δ x}$ ;

Bước 3. Tính $lim_{Δ x \to 0} \frac{Δ y}{Δ x}$ .

Nhận xét: nếu thay $x_{0}$ bởi $x$ ta có định nghĩa và quy tắc tính đạo hàm của hàm số $y = f (x)$ tại điểm $x \in (a; b)$ .

3. Đạo hàm của tổng, hiệu, tích, thương

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định. Khi đó

$\begin{array}{l} {(u + v)}^{'} = u^{'} + v^{'}; \\ {(u - v)}^{'} = u^{'} - v^{'}; \\ {(u v)}^{'} = u^{'} v + u v^{'}; \\ {(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}} (v = v (x) \neq 0); \end{array}$

${(C . v)}^{'} = C . v^{'}$ (C là hằng số);

${(\frac{1}{v})}^{'} = - \frac{v^{'}}{v^{2}} (v \neq 0)$ .

4. Đạo hàm của hàm hợp

Nếu hàm số u = g(x) có đạo hàm tại x là $u_{x}^{'}$ và hàm số y = f(u) có đạo hàm tại y là $y_{u}^{'}$ thì hàm hợp y = f(g(x)) có đạo hàm tại x là $y_{x}^{'} = y_{u}^{'} . u_{x}^{'}$ .

5. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp

Lý thuyết Các quy tắc tính đạo hàm (Chân trời sáng tạo 2024) hay, chi tiết | Toán lớp 11 (ảnh 1)

6. Đạo hàm cấp hai

Cho hàm số y = f(x) có đạo hàm tại mọi điểm $x \in (a; b)$ thì ta có hàm số $y^{'} = f^{'} (x)$ xác định trên (a; b).

Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).

$f^{″} (x) = {(f^{'} (x))}^{'}$ .

7. Quan hệ giữa tính liên tục và sự tồn tại đạo hàm

Định lí. Nếu hàm số $y = f (x)$ có đạo hàm tại $x_{0}$ thì nó liên tục tại $x_{0}$ _.

Chú ý.

Định lí trên tương đương với khẳng định : Nếu $y = f (x)$ gián đoạn tại $x_{0}$ thì nó không có đạo hàm tại điểm đó.

Mệnh đề đảo của định lí không đúng. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

8. Ý nghĩa hình học của đạo hàm

Nếu tồn tại, $f^{'} (x_{0})$ là hệ số góc của tiếp tuyến của đồ thị hàm số $y = f (x)$ tại điểm $M_{0} (x_{0}; f (x_{0}))$ . Khi đó phương trình tiếp tuyến của đồ thị tại điểm $M_{0} (x_{0}; f (x_{0}))$ là

$y - f (x_{0}) = f^{'} (x_{0}) (x - x_{0})$

9. Ý nghĩa vật lí của đạo hàm

$v (t) = s^{'} (t)$ là vận tốc tức thời của chuyển động $s = s (t)$ tại thời điểm $t$ .

B. Bài tập Đạo hàm

Bài tập đạo hàm hàm số

Bài 1: Đạo hàm của hàm số y = (2x⁴ - 3x² - 5x)(x² - 7x) bằng biểu thức nào dưới đây?

A. (8x³ - 6x - 5)(2x - 7)

B. (8x³ - 6x - 5)(x² - 7x) - (2x⁴ - 3x² - 5x)(2x - 7)

C. (8x³ - 6x - 5)(x² - 7x)+(2x⁴ - 3x² - 5x)(2x - 7)

D. (8x³ - 6x - 5) + (2x - 7)

Lời giải:

Đáp án: C

Áp dụng công thức đạo hàm hàm hơp (uv)’= u’v + uv’ ta có:

y' = (8x³ - 6x - 5)(x² - 7x) + (2x⁴ - 3x² - 5x)(2x - 7)

Chọn đáp án là C

Bài 2: Đạo hàm của hàm số 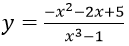Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: D

Áp dụng công thưc đạo hàm hàm hơp Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án ta có:

Chọn đáp án là D

Bài 3: Đạo hàm của hàm số 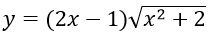Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Ta có:

Bài 4: Đạo hàm của hàm số f(t) = a³t⁴ - 2at² + 3t - 5a bằng biểu thức nào sau đây?

A. 4a³t³ - 4at + 3

B. 3a²t⁴ - 2t² - 5

C. 12a²t³ - 4at - 2

D. 4a³t³ - 4at - 5

Lời giải:

Đáp án: A

f'(t) = 4a³t³ - 4at + 3

Chọn đáp án là A

Bài 5: Đạo hàm của hàm số 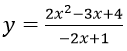Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Bài 6: Đạo hàm cuả hàm số 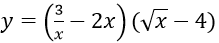Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Bài 7: Đạo hàm của hàm số 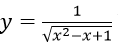Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài 8: Đạo hàm của hàm số 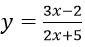Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 9: Đạo hàm của hàm số 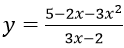Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: C

Bài 10: Đạo hàm của hàm số:

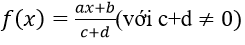
Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 11: Đạo hàm của hàm số f(x) = a³ - 3at² - 5t³(với a là hằng số) bằng biểu thức nào sau đây?

A. 3a² - 6at - 15t²

B. 3a² - 3t²

C. -6at - 15t²

D. 3a² - 3t² - 6at - 15t²

Lời giải:

Đáp án: C

f(t) = a³ - 3at² - 5t³

f'(t) = -6at - 15t²

Chọn đáp án là C

Bài 12: Đạo hàm của hàm số 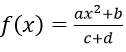Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào sau đây?

Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 13: Đạo hàm của hàm số f(x) = t²x + tx² bằng biểu thức nào sau đây?

A. 2tx + x²

B. t² + 2tx

C. 2x + 2tx

D. 2tx + 2tx

Lời giải:

Đáp án: B

Biến là x (t là hằng số), do đó B đúng

Bài 14: Đạo hàm của hàm số 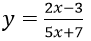Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào sau đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài 15: Đạo hàm của hàm số 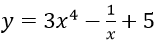Chuyên đề Toán lớp 11 | Chuyên đề: Lý thuyết - Bài tập Toán 11 có đáp án bằng biểu thức nào sau đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài tập trắc nghiệm

Câu 1: Đạo hàm của hàm số y= - 18√2 là:

A . - 18 B. 18 C. - 18√2 D. 0

Lời giải:

Hàm số y= - 18√2 là hàm hằng nên y'=0

Chọn D.

Câu 2: Cho hàm số y= f(x) = - 2x + 10. Trong các mệnh đề sau, mệnh đề nào đúng?

A.f' (x)=2 B. f'(x)= - 2 C. f' (x)=10 D. f' (x)=-10

Lời giải:

Ta có: f' (x)=(-2x+10)'=(-2x)'+( 10)'=-2-0= -2

Chọn B.

Câu 3: Cho hàm số y= -x² - 7x + 8. Tính đạo hàm của hàm số đã cho

A. –x- 7 B. 2x + 7

C. 2x - 7 D. -2x- 7

Lời giải:

Ta có: f' (x)=(-x²-7x+8)'=-(x )'-7.(x)'+(8)'=-2x-7.1+0

⇒ f’(x)= -2x - 7

Chọn D.

Câu 4: Đạo hàm của hàm số y= f(x)= 2x⁴ + 2x² + x + 28 là

A. 8x³ +2x + 1 B. 8x³ +4x+ 1

C. 8x⁴ + 4x + 1 D. 4x³ +2x+ 1

Lời giải:

Ta có: f' (x)=(2x⁴+2x²+x+28)'=2(x⁴ )'+2(x² )'+(x)'+(28)'

⇒f’(x)= 8x³ +4x + 1

Chọn B.

Câu 5: Đạo hàm của hàm số y= f(x)= (x- 6)(8- 4x) bằng biểu thức nào sau đây?

A. 32- 8x B. 6x- 24 C. - 4x + 32 D. 2x+ 16

Lời giải:

Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

f' (x)=( x-6)'.( 8-4x)+( x-6).(8-4x)'

⇒ f'(x)= 1.( 8 - 4x)+ (x- 6). (-4) = 8- 4x – 4x + 24 = -8x + 32

Chọn A.

Câu 6: Đạo hàm của hàm số y=f(x)= (x+ 2)( x- 3) bằng biểu thức nào?

A. x+ 1 B. 2x- 1 C. 3x+ 2 D. x²- 1

Lời giải:

+ Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

⇒ f' (x)=(x+2)'.(x-3)+(x+2).(x-3)'

= 1.(x-3) + (x+2). 1 = x- 3+ x+ 2

= 2x - 1

Chọn B.

Câu 7: Tính đạo hàm của hàm số y= (x-6)/(2x+3)?

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Câu 8: Tính đạo hàm của hàm số y= (x²+x+1)/(1-x)?

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Câu 9: Tính đạo hàm của hàm số: y= (x+2)/(x²-1)?

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Câu 10: Tính đạo hàm của hàm số: y=4√x - 4x⁴ + 2x?

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Câu 11: Tính đạo hàm của hàm số: y=(2√x-2).( 2x+1)

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

+ Áp dụng công thức ( u.v)'=u'.v+uv' ta có:

y'=( 2√x-2)' ( 2x+1)+( 2√x-2).(2x+1)'

⇒ y'= 2.1/(2√x) (2x+1)+(2√x-2).2

= 2√x+ 1/√x+ 4√x-4= 6√x+ 1/√x-4

Chọn A.

Câu 12: Tính đạo hàm của hàm số y= x³/3+2x²- 1/x?

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Câu 13: Tính đạo hàm của hàm số: y= (x²+2x)/(x²-3x+1)

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Lời giải:

Áp dụng công thức đạo hàm của một thương ta có:

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Bài tập tự luyện

Bài 1. Đạo hàm của hàm số y = f(x) = (x² + x + 1)(x – 5).

Bài 2. Tính đạo hàm của hàm số y = (x + 5)²(x – 9).

Bài 3. Tính đạo hàm của hàm số y = $(\sqrt{x} - 1) (x + 1)$ .

Bài 4. Tính đạo hàm của hàm số y = $(\frac{1}{\sqrt{x}} - 3) (2 \sqrt{x} + 1)$ .

Bài 5. Tính đạo hàm của hàm số f(x) = $\frac{1}{3 x + 3} . (2 \sqrt{x} - 2)$ .

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm