Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ Phương trình logarit là gì? Các cách giải phương trình logarit và bài tập, tài liệu tuyển chọn Phương trình logarit là gì? Các cách giải phương trình logarit và bài tập đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Phương trình logarit là gì? Các cách giải phương trình logarit và bài tập
1. Định nghĩa
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
2. Phương trình lôgarit cơ bản
• loga x = b ⇔ x = ab (0 < a ≠ 1).
• loga f(x) = loga g(x) 
3. Các bước giải phương trình logarit bằng cách đưa về cùng cơ số
* Bước 1. Tìm điều kiện của phương trình (nếu có).
* Bước 2. Sử dụng định nghĩa và các tính chất của lôgarit để đưa các lôgarit có mặt trong phương trình về cùng cơ số.
* Bước 3.Biến đổi phương trình về phương trình lôgarit cơ bản đã biết cách giải.
* Bước 4. Kiểm tra điều kiện và kết luận.
*Ví dụ minh họa
Bài 1: Giải phương trình: log2 x + log3 x + log4 x = log20 x.
Hướng dẫn:
Điều kiện của phương trình là x > 0.
Với điều kiện trên phương trình đã cho tương đương với phương trình
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {1}.
Bài 2: Giải phương trình
Hướng dẫn:
Tập nghiệm của phương trình đã cho là {1;2}.
Bài 3: Giải phương trình
Hướng dẫn:
Tập nghiệm của phương trình đã cho là {3}.
4. Giải phương trình logarit bằng cách mũ hóa
*Phương pháp giải
1. Phương trình lôgarit cơ bản
• loga x = b ⇔ x = ab (0 < a ≠ 1).
• loga f(x) = loga g(x) 
2. Cơ sở của phương pháp mũ hoá
loga f(x) = g(x) (0 < a ≠ 1) ⇔ f(x) = ag(x)
*Ví dụ minh họa
Bài 1: Giải phương trình log2 (x+3)=1.
Hướng dẫn:
log2 (x+3) = 1 ⇔ x+3 = 2 ⇔ x = -1
Bài 2: Giải phương trình log(25x - 22x+1) = x.
Hướng dẫn:
log(25x-22x+1 )=x ⇔ 25x-22x+1=10x ⇔ 25x-2.4x=10x
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là 
Bài 3: Giải phương trình log2 (9-2x )=3-x.
Hướng dẫn:
log2 (9-2x ) = 3-x ⇔ log2 (9-2x ) = log2 23-x ⇔ 9-2x=23-x ⇔ 9-2x=8/2x ⇔ 22x-9.2x+8=0
Tập nghiệm của phương trình đã cho là {0;3}.
5. Giải phương trình logarit bằng cách đặt ẩn phụ
*Phương pháp giải
1. Phương trình lôgarit cơ bản
• logax = b ⇔ x = ab (0 < a ≠ 1).
• logaf(x)=logag(x) 
2. Các bước giải phương trình bằng phương pháp đặt ẩn phụ
Giải phương trình: f[logag(x)] = 0 (0 < a ≠ 1).
• Bước 1: Đặt t = logag(x) (*).
• Bước 2: Tìm điều kiện củat (nếu có).
• Bước 3: Đưa về giải phương trình f(t) = 0 đã biết cách giải.
•Bước 4: Thay vào (*) để tìm x.
3. Một số lưu ý quan trọng khi biến đổi
1) logaf2(x) = 2loga|f(x)|
2) logaf2k(x) = 2kloga|f(x)|
3) logaf2k+1(x) = (2k+1)logaf(x)
4) loga(f(x)g(x)) = loga|f(x)| + loga|g(x)|
*Ví dụ minh họa
Bài 1: Giải phương trình log23 x - 4log3x + 3 = 0.
Hướng dẫn:
Điều kiện của phương trình là x > 0.
Đặt log3x = t. Khi đó phương trình đã cho trở thành
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3;27}.
Bài 2: Giải phương trình
Hướng dẫn:
Khi đó phương trình đã cho trở thành
Tập nghiệm của phương trình đã cho là {10; 100}.
Bài 3: Giải phương trình
Hướng dẫn:
Điều kiện của phương trình là x > 0.
Khi đó phương trình đã cho trở thành
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3√3; 3-√3 }.
6. Sử dụng tính đơn điệu để giải phương trình logarit
*Phương pháp giải
Giả sử phương trình có dạng f(x) = g(x) (*)
• Bước 1: Nhẩm được một nghiệm x0 của phương trình (thông thường chọn nghiệm lân cận 0).
• Bước 2: Xét các hàm số y = f(x)(C1) và y = g(x)(C2). Ta cần chứng minh một hàm đồng biến và một hàm nghịch biến hoặc một hàm đơn điệu và một hàm không đổi. Khi đó (C1) và (C2) giao nhau tại một điểm duy nhất có hoành độ x0. Đó chính là nghiệm duy nhất của phương trình (*).
Hoặc đưa phương trình về dạng f(x) = 0
• Bước 1: Nhẩm được hai nghiệm x1; x2 của phương trình (thường chọn nghiệm lân cận 0).
• Bước 2: Xét các hàm số y = f(x). Ta cần chứng minh f'(x) = 0 có nghiệm duy nhất và f'(x) đổi dấu khi đi qua nghiệm đó. Từ đây suy ra phương trình f(x) = 0 có nhiều nhất hai nghiệm.
Hoặc:
• Bước 1: Biến đổi phương trình về dạng f(u) = f(v) .
• Bước 2: Chứng minh hàm f(x)là hàm đơn điệu, suy ra u = v
*Ví dụ minh họa
Bài 1: Giải phương trình log3 (x+2) + log7 (3x+4) = 2
Hướng dẫn:
Phương trình có một nghiệm x = 1
f(x) = log3(x+2) + log7(3x+4) ⇒ f'(x) > 0, nên f(x) đồng biến trên tập xác định ;g(x)=2là hàm hằng. Nên phương trình đã cho có một nghiệm duy nhất x = 1
Bài 2: Giải phương trình log2 (x2-x-6)+x=log2 (x+2)+4
Hướng dẫn:
Phương trình (2)có một nghiệm x = 4
f(x) = log2(x-3), đồng biến trên tập xác định; g(x) = 4-x nghịch biến trên tập xác định. Nên phương trình đã cho có một nghiệm duy nhất x = 4.
Bài 3: Giải phương trình
Hướng dẫn:
⇔ log2 (x2-x+1)-log2 (2x2-4x+3) = x2-3x+2 ⇔ log2 (x2-x+1) + (x2-x+1) = log2 (2x2-4x+3)+(2x2-4x+3) (3)
Xét hàm số f(t) = log2 t+t có f'(t) > 0 nên hàm số đồng biến trên tập xác định. Khi đó có f(x2-x+1) = f(2x2-4x+3) ⇒ x2-x+1 = 2x2-4x+3 ⇔ x2-3x+2=0
Nên phương trình đã cho có tập nghiệm là {1;2}
7. Cách giải phương trình logarit chứa tham số
*Phương pháp giải
♦ Dạng toán Tìm m để phương trình có số nghiệm cho trước:
• Bước 1. Tách m ra khỏi biến số x và đưa về dạng f(x)=A(m).
• Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D.
• Bước 3. Dựa vào bảng biến thiên để xác định giá trị tham số A(m) để đường thẳng y=A(m) nằm ngang cắt đồ thị hàm số y=f(x).
• Bước 4. Kết luận các giá trị của A(m) để phương trình f(x)=A(m) có nghiệm (hoặc có k nghiệm) trên D.
♦ Lưu ý
• Nếu hàm số y=f(x) có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị A(m) cần tìm là những m thỏa mãn:
• Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng y=A(m) nằm ngang cắt đồ thị hàm số y=f(x) tại k điểm phân biệt.
Hoặc sử dụng điều kiện có nghiệm của phương trình bậc hai với lưu ý sau.
♦ Nhắc lại: Phương trình bậc hai có hai nghiệm thỏa mãn
Hoặc sử dụng định lí đảo về dấu tam thức bậc hai:
*Ví dụ minh họa
Bài 1: Tìm tham số thực m để phương trình: log23 x+log3x+m=0 có nghiệm.
Hướng dẫn:
Tập xác định D=(0;+∞).
Đặt log3x=t. Khi đó phương trình trở thành t2+t+m=0 (*)
Phương trình đã cho có nghiệm khi phương trình (*) có nghiệm: Δ=1-4m ≥ 0 ⇔ m ≤ 1/4.
Vậy để phương trình có nghiệm thực thì: m ≤ 1/4.
Bài 2: Tìm tham số m để phương trình log2(5x-1)log4(2.5x-2)=m có nghiệm thực x ≥ 1.
Hướng dẫn:
Điều kiện: 5x-1 > 0 ⇔ x > 0
log2(5x-1)log4(2.5x-2)=m
⇔ log2(5x-1) 1/2 log2(2(5x-1))=m
⇔ log2(5x-1)(1+log2(5x-1))=2m
⇔ log22 (5x-1)+log2(5x-1)=2m
Đặt log2(5x-1)=t. Khi đó phương trình đã cho trở thành t2+t-2m=0 (*)
Phương trình đã cho có nghiệm x ≥ 1 khi phương trình (*)có nghiệm
Vậy phương trình có nghiệm thực x ≥ 1 thì m ≥ 3.
Bài 3: Tìm tham số thực m để phương trình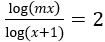 
có nghiệm thực duy nhất.
Hướng dẫn:
⇔ log(mx)=2log(x+1)
⇔ log(mx)=log(x+1)2
⇔ mx=(x+1)2 ⇔ x2+(2-m)x+1=0 (*)
Phương trình đã cho có nghiệm duy nhất khi phương trình (*)có một nghiệm thỏa mãn
TH1: phương trình (*) có hai nghiệm thỏa mãn -1 < x1 ≤ x2:
TH2: phương trình (*) có hai nghiệm thỏa mãn x1 < -1 < x2: af(-1) < 0 ⇔ m < 0.
Các giá trị m cần tìm 
8. Bài tập minh họa
Bài 1: Giải phương trình: log2 x + log3 x + log4 x = log20 x.
Hướng dẫn:
Điều kiện của phương trình là x > 0.
Với điều kiện trên phương trình đã cho tương đương với phương trình
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {1}.
Bài 2: Giải phương trình
Hướng dẫn:
Tập nghiệm của phương trình đã cho là {1;2}.
Bài 3: Giải phương trình
Hướng dẫn:
Tập nghiệm của phương trình đã cho là {3}.
9. Bài tập tự luyện
Bài 1: Giải phương trình
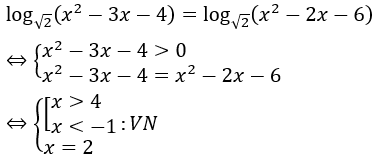
Phương trình đã cho vô nghiệm.
Bài 2: Giải phương trình
Điều kiện của phương trình là
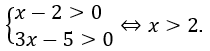
Với điều kiện trên phương trình đã cho tương đương với phương trình
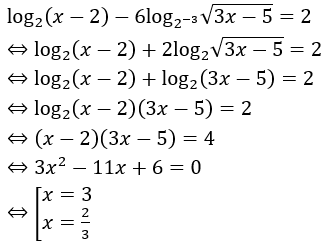
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {3}.
Bài 3: Giải phương trình
Điều kiện của phương trình là
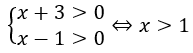
Với điều kiện trên phương trình đã cho tương đương với phương trình
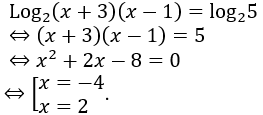
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {2}.
Bài 4: Giải phương trình
Điều kiện của phương trình là x > 0.
Với điều kiện trên phương trình đã cho tương đương với phương trình
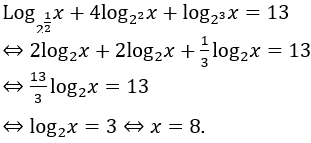
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {8}.
Bài 5: Giải phương trình
Điều kiện
Vậy phương trình có nghiệm 
Bài 6: Giải phương trình
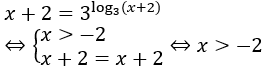
Bài 7: Giải phương trình
Tập xác định 0 < x < 2a.
Bài 8: Giải phương trình
Điều kiện của phương trình là
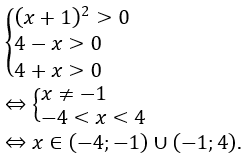
Với điều kiện trên phương trình đã cho tương đương với phương trình
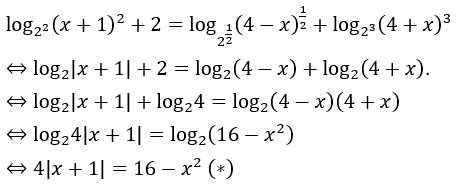
+) Với x ∈ (-4;-1):
Khi đó (*) trở thành 4(-x-1) = 16-x2 ⇔ x2-4x-20= 0
+) Với x ∈ (-1;4):
Khi đó (*) trở thành 4(x+1) = 16-x2 ⇔ x2+4x-12 = 0
Vậy tập nghiệm của phương trình đã cho là {2; 2-2√6}.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
