Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Số thực là gì? Tập hợp R, tính chất và các dạng bài tập, tài liệu gồm đầy đủ về lý thuyết Số thực, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Số thực là gì? Tập hợp R, tính chất và các dạng bài tập
A. Lý thuyết Số thực
1. Khái niệm số thực
- Khái niệm: Số hữu tỉ và số vô tỉ được gọi chung là số thực.
- Kí hiệu: Tập hợp số thực được kí hiệu là .
Ví dụ:
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số vô tỉ nên cũng là một số thực.
Chú ý:
• Cũng như số hữu tỉ, mỗi số thực a đều có một số đối kí hiệu là – a.
Ví dụ: Số đối của là ; số đối của là .
- Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
- Vì mỗi điểm trên trục số đều biểu diễn một số thực nên các số thực lấp đầy trục số. Người ta cũng gọi trục số là trục số thực.

- Trong tập hợp số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
Ví dụ: Tính giá trị của biểu thức ta làm như sau:
(Tính chất giao hoán)
(Tính chất kết hợp)
(Tổng hai số đối nhau luôn bằng 0)
(Cộng với số 0)
2. So sánh hai số thực
• Các số thực đều được viết dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể so sánh hai số thực bằng cách viết dưới dạng số thập phân.
• Cũng như các số hữu tỉ, ta có
Với hai số thực a và b bất kì ta luôn có a = b hoặc a < b hoặc a > b.
Cho ba số thực a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).
• Trên trục số thực, nếu a < b thì điểm a nằm trước điểm b. Các điểm nằm trước gốc O biểu diễn các số âm, các điểm nằm sau gốc O biểu diễn các số dương.
• x là số âm, ta viết: x < 0; x là số dương, ta viết: x > 0.
Ví dụ:
+ So sánh và – 1,5 ta làm như sau: nên .
+ So sánh và ta làm như sau: Vì và nên .
+ Ta có nên điểm biểu diễn của trên trục số nằm giữa hai điểm A và B.

Chú ý:
• Nếu 0 < a < b thì .
Ví dụ: 0 < 3 < 5 thì .
3. Tính chất của số thực R
Bất kỳ số thực khác không là số âm hoặc số dương
Tổng hay tích của 2 số thực không âm là một số thực không âm
Số thực là tập hợp vô hạn, có thể đếm được của các số thực
Có hệ thống các tập hợp con vô hạn có thể đếm được của các số thực
Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục
Số thực có thể biểu thị bằng biểu diễn thập phân.
4. Giá trị tuyệt đối của một số thực
• Với số thực a tùy ý, ta có khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là .
• Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.
• Giá trị tuyệt đối của 0 là 0.
• Giá trị tuyệt đối của một số dương là chính nó.
• Giá trị tuyệt đối của một số âm là số đối của nó.
Ví dụ:
+ Số 1 và –1 là hai số đối nhau và có cùng giá trị tuyệt đối là 1

+ Số nên
+ Số nên
5. Mối quan hệ giữa các tập hợp số
- Tập hợp các số tự nhiên .
- Tập hợp các số nguyên gồm các số tự nhiên và số nguyên âm:
.
- Tập hợp các số hữu tỉ gồm các số được viết dưới dạng phân số , với .
Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
- Tập hợp các số thực gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn.
- Mối quan hệ giữa các tập hợp số: .
Ví dụ: Cho tập hợp B = {– 1; 2; 4; 10}.
- Tập hợp B chứa số – 1 không phải là số tự nhiên nên B không là tập con của .
- Tập hợp B gồm các số nguyên: – 1; 2; 4; 10 nên B là tập con của .
- Các số nguyên cũng là các số hữu tỉ và cũng là các số thực, nên B cũng là tập con của và .
6. Các tập con thường dùng của
- Một số tập con thường dùng của tập số thực :
+ Khoảng:
+ Đoạn
+ Nửa khoảng
‑ Kí hiệu + ∞: Đọc là dương vô cực (hoặc dương vô cùng).
‑ Kí hiệu – ∞: Đọc là âm vô cực (hoặc âm vô cùng).
‑ a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.
Ví dụ:
+ Ta có: 5 < x ≤ 10 thì ta viết x ∈ (5; 10].
+ Ta có: D = {x | x < 3} = (– ∞; 3).
B. Các dạng bài tập về số thực
Dạng 1: Các câu hỏi và bài tập về định nghĩa các tập hợp số
1. Phương pháp giải:
- Nắm vững các ký hiệu tập hợp số:
: tập hợp các số tự nhiên
: tập hợp các số nguyên
: tập hợp các số hữu tỉ
I: tập hợp các số vô tỉ
: tập hợp các số thực
- Nắm vững quan hệ giữa các tập hợp số nói trên: ; ;
- Các kí hiệu; dùng để so sánh giữa phần tử với tập hợp.
- Các kí hiệu dùng để so sánh giữa các tập hợp với nhau.
2. Ví dụ minh họa
Ví dụ 1: Điền kí hiệu thích hợp vào ô trống:
 Giải:
Giải:


Dạng 2: So sánh các số thực
1. Phương pháp giải:
Cần nắm vững:
- Với hai số thực x, y bất kỳ, ta luôn có x = y hoặc x < y hoặc x > y.
- Các số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là các số thực âm. Số 0 không là số thực dương cũng không là số thực âm.
- Việc so sánh các số thực dương làm tương tự như so sánh các số hữu tỉ.
- Với a, b là hai số thực dương, nếu a > b thì
2. Ví dụ minh họa:
Ví dụ 2: Sắp xếp các số thực: theo thứ tự từ bé đến lớn.
Giải:
Ta có:
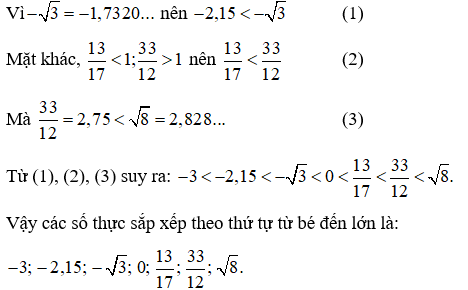
Dạng 3: Tìm một số chưa biết trong một đẳng thức
1. Phương pháp giải:
- Sử dụng tính chất của các phép toán.
- Sử dụng quan hệ giữa các số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương trong một phép chia.
- Sử dụng quy tắc dấu ngoặc, chuyển vế.
2. Ví dụ minh họa:
Ví dụ 3: Tìm x, biết:
a)
b)
Giải:
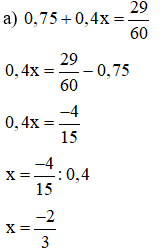
Vậy là giá trị cần tìm.
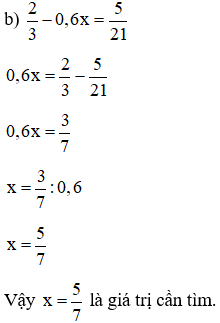
Dạng 4: Tìm giá trị của biểu thức
1. Phương pháp giải:
- Thực hiện phối hợp các phép tính cộng, trừ, nhân, chia, lũy thừa, chú ý thực hiện đúng theo thứ tự đã quy định.
- Rút gọn các phân số khi có thể.
- Chú ý vận dụng tính chất các phép toán để tính toán được thuận tiện.
2. Ví dụ minh họa:
Ví dụ 4: Tính giá trị của các biểu thức:
Giải:
= (0,8.7 + 0,64).(1,25.7 - 0.8.1,25) + 31,64
= (5,6 + 0,64).(8,75 - 1) + 31,64
= 6,24.7.75 + 31.64
= 48,36 + 31,64
= 80.
C. Bài tập vận dụng
1. Bài tập trắc nghiệm
Bài 1. Xác định tất cả giá trị của x để ?
A. { 7 };
B. { -7 };
C. {};
D. {7; -7 }.
Hướng dẫn giải
Đáp án đúng là: D
x2 = 49
x2 = 72 = (– 7)2
x = 7 hoặc x = – 7.
Vậy các giá trị x cần tìm là {7; – 7}.
Bài 2. Cho hình dưới đây, hãy cho biết điểm A chỉ số thực nào?
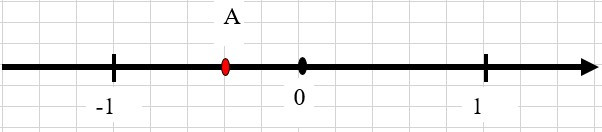
A. ;
B. ;
C. ;
D..
Hướng dẫn giải
Đáp án đúng là: D
Đoạn thẳng đơn vị được chia thành 5 phần bằng nhau. Đoạn thẳng OA chiếm 2 đơn vị mới (đơn vị mới bằng đơn vị cũ). Mà A nằm bên trái O, do đó A biểu diện số âm.
Vậy điểm A biểu diễn số .
Bài 3. Liệt kê các phần tử của tập hợp }?
A. { 1; 2; 3; 4 };
B. {-1; -2; -3; -4 };
C. {-1; -2; 0; 1; 2 };
D. {-1; -2; -3; 1; 2; 3 }.
Hướng dẫn giải
Đáp án đúng là: C
hoặc
Nếu thì thì x={0; 1; 2} (do x là số nguyên)
Nếu thì thì x={-1; -2} (do x là số nguyên)
2. Bài tập tự luận
Bài 1. So sánh:
a) 28,03 và 28,0(23)
b) và
c) –2 và
d) –19,11 và –19,(1)
e) và 3
f) và
Hướng dẫn giải
a) Vì 3 > 2 nên 28,03 > 28,02323… nên 28,03 > 28,0(23)
b) Vì nên <
c) Vì 2 > 0 nên . Mà 4 > 3 nên
Do đó . Vậy –2 <
d) Vì 0 < 1 nên 19,110 < 19,111 nên –19,11 > –19,(1)
e) nên
f) (vì ) và (vì 3 > 0). Mà 5 > 3 nên >
Bài 2. Cho tập hợp A = {1,9; –2,(6); 10; ; ; π; ; }. Bằng cách liệt kê các phần tử, hãy viết:
a) Tập hợp B gồm các số hữu tỉ thuộc tập hợp A;
b) Tập hợp C gồm các số vô tỉ thuộc tập hợp A;
c) Tập hợp D gồm các số thực thuộc tập hợp A;
d) Tập hợp A’ gồm các số đối của các số thuộc tập hợp A.
Hướng dẫn giải
a) Ta có:
Vì 1,9; -2,(6); 10; ; là số hữu tỉ nên B = {1,9; –2,(6); 10; ; ; }
b) Vì là số vô tỉ nên C = {π; }
c) Vì các số hữu tỉ và các số vô tỉ đều là số thực nên D = {1,9; –2,(6); 10; ; ; π; ; }
d) Số đối của 1,9 là – 1,9
Số đối của – 2,(6) là 2,(6)
Số đối của 10 là -10
Số đối của là
Số đối của là
Số đối của là –
Số đối của là
Số đối của là
Vậy A’ = {–1,9; 2,(6); –10; –; ; –π; ; }
Bài 3. Tính giá trị tuyệt đối của các số sau:
a)
b)
c)
d)
Hướng dẫn giải
a) Vì < 0 nên
b) Vì > 0 nên
c) Vì < 0 nên
d) Vì > 0 nên
3. Bài tập tự luyện
Bài 1: Điền dấu thích hợp vào ô trống.

Bài 2: So sánh các số thực sau:
a) 22,099 và 22,09(2209)
b) và 1,8(3)
Bài 3: Sắp xếp các số thực sau theo thứ tự tăng dần:
0,466; ; 0,4636363...; 0,463736; 0,4656365…
Bài 4: Sắp xếp các số thực: theo thứ tự từ nhỏ đến lớn.
Bài 5: Tính giá trị của biểu thức:
Bài 6: So sánh:
a) và 3.
b) và
Bài 7: Tính bằng cách hợp lí:
A = (+0,35) + [(+52,7) + (– 7,35) + (+4,3)]
B = (– 45,7) + [(+5,7) + (+5,75) + (– 0,75)]
C = [(+19,5) + (– 23)] + [(– 7) + (+10,5)]
Bài 8: Tìm x:
a) 3,5.x + (– 1,5).x + 3,2 = – 5,4
b) (– 7,2).x + 3,7.x + 2,7 = – 7,8
c)
Bài 9: a) Điền số thích hợp vào các đẳng thức:
b) Chứng tỏ mọi ta có:
Bài 10: Tìm x nguyên để các biểu thức sau có giá trị nguyên:
Hướng dẫn giải:
Bài 1:
a.
b.
c.
d.
Bài 2: Đáp án:
a) >
b) =
Bài 3:
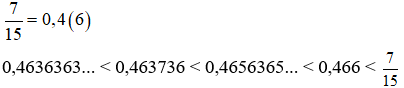
Bài 4:
Ta có
Mà
Bài 5:
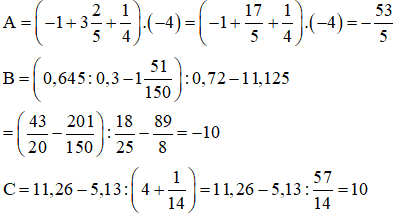
Bài 6:
a)
b)
Bài 7:
A = 50 B = – 35 C = 0
Bài 8:
a) 3,5.x + (– 1,5).x + 3,2 = – 5,4
x(3,5 – 1,5) = – 5,4 – 3,2
2x = – 8,6
x = – 4,3
b) (– 7,2).x + 3,7.x + 2,7 = – 7,8
x(– 7,2 + 3,7) = – 7,8 – 2,7
x(– 3,5) = – 10,5
x = 3
c.
Bài 9:

Bài 10: