Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Cực trị của hàm số là gì? Lý thuyết và các dạng bài tập, tài liệu gồm đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án và lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Cực trị của hàm số là gì? Lý thuyết và các dạng bài tập
1. Định nghĩa:
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là -∝; b là +∝) và điểm xo ∈ (a; b) .
- Nếu tồn tại số h > 0 sao cho f(x) < f(xo) với mọi x ∈ (xo - h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực đại tại xo .
- Nếu tồn tại số h > 0 sao cho f(x) > f(xo) với mọi x ∈ (xo - h; xo + h) và x ≠ xo thì ta nói hàm số f(x) đạt cực tiểu tại xo .
2. Điều kiện đủ để hàm số có cực trị:
Giả sử hàm số y = f(x) liên tục trên K = (xo - h; xo + h) và có đạo hàm trên K hoặc trên K \ {xo}, với h > 0 .
- Nếu f'(x) > 0 trên khoảng (xo - h; xo) và f'(x) < 0 trên (xo; xo + h) thì xo là một điểm cực đại của hàm số f(x).
- Nếu f'(x) < 0 trên khoảng (xo - h; xo) và f'(x) > 0 trên (xo; xo + h) thì xo là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
* Chú ý.
- Nếu hàm số y = f(x) đạt cực đại (cực tiểu) tại xo thì xo được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(xo) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCĐ(fCT) , còn điểm M(xo; f(xo)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
- Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
1. Quy tắc tìm cực trị của hàm số
- Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x) . Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
- Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu xi (i = 1; 2; 3;...) là các nghiệm của nó.
Bước 3. Tính f"(x) và f"(xi).
Bước 4. Dựa vào dấu của f"(xi) suy ra tính chất cực trị của điểm xi.
2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0)
Ta có y'= 3ax2 + 2bx + c
- Đồ thị hàm số có hai điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt ⇔ b2 - 3ac > 0. Khi đó đường thẳng qua hai điểm cực trị đó là :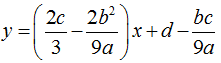 
.
- Bấm máy tính tìm ra đường thẳng đi qua hai điểm cực trị :
Hoặc sử dụng công thức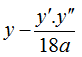 
.
- Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc ba là:
3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt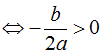 
.
Khi đó ba điểm cực trị là: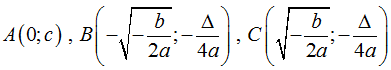 
với Δ = b2 - 4ac
Độ dài các đoạn thẳng: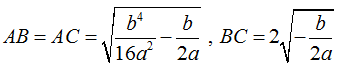 
.
Các kết quả cần ghi nhớ:
- ΔABC vuông cân ⇔ BC2 = AB2 + AC2
- ΔABC đều ⇔ BC2 = AB2
- 
, ta có: 
- 
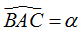
- Bán kính đường tròn ngoại tiếp ΔABC là 
- Bán kính đường tròn nội tiếp ΔABC là 
- Phương trình đường tròn ngoại tiếp ΔABC là: 
Ví dụ 1: Tìm đường thẳng đi qua hai điểm cực trị của đồ thị hàm số: y = x3 + 3x2 - x + 2
Hướng dẫn:
Bấm máy tính: MODE 2
Ví dụ 2: Tìm đường thẳng đi qua hai điểm cực trị ( nếu có ) của đồ thị hàm số: y = x3 - 3x2 + m2x + m
Hướng dẫn:
Bấm máy tính: MODE 2
Ta có:
Vậy đường thẳng cần tìm:
4. Bài tập tự luyện
Câu 1: Cho hàm số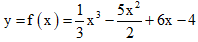 
. Tìm mệnh đề đúng?
A. Điểm cực đại của đồ thị hàm số là x = 2.
B. Điểm cực tiểu của đồ thị hàm số là x = 2.
C. Điểm cực đại của đồ thị hàm số là (2; 2/3).
D. Điểm cực tiều của hàm số là (3; 1/2).
- Tập xác định: D = R.
y' = x2 - 5x + 6; y' = 0 
y'' = 2x - 5 và y''= 2x - 5
Do y''(2) = - 1 < 0 nên x = 2 là điểm cực đại của hàm số.
Vì y''(3) = 1 > 0 nên x = 3 là điểm cực tiểu của hàm số.
- Suy ra đồ thị hàm số đã cho có một điểm cực đại (2; 2/3), một điểm cực tiểu (3; 1/2)
Suy ra chọn đáp án C.
Câu 2: Tìm cực trị của hàm số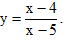 
.
A. x = 5 B. x = 4
C. (4;0) D. Không có điểm cực trị
- Tập xác định: D = R\{5}.
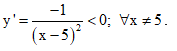
Suy ra hàm số không có cực trị.
Suy ra chọn đáp án D.
Câu 3: Hàm số y= -x3 + 3x2 + 1 đạt cực tiểu tại:
A. x = 0 B. x = 2
C. Không có cực tiểu D. Đáp án khác
- TXĐ: D = R.
Ta có: y' = (-x3 + 3x2 + 1)' = -3x2 + 6x, y' = 0 ⇔ -3x(x - 2) = 0 
Do y'' = -6x + 6 và y''(0) = 6 > 0 nên x = 0 là điểm cực tiểu của hàm số.
Vì y''(2) = -6 < 0 nên x = 2 là điểm cực đại của hàm số.
Nhận xét: Chúng ta cũng có thể dùng bảng biến thiên để tìm cực đại, cực tiểu của hàm số.
- Bảng biến thiên hàm số: y = -x3 + 3x2 + 1
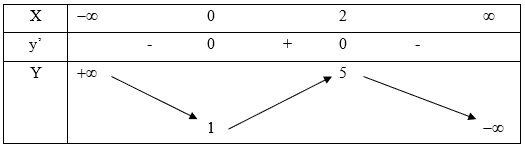
Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực tiểu
Suy ra chọn đáp án A.
Câu 4: Khẳng định nào sau đây là sai:
A.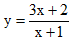 
có đạt cực tiểu tại – 1.
B.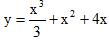 
không có cực trị.
C. y = x4 + 6x2 + 2 đạt cực tiểu là 0.
D. Nếu đạo hàm không đổi dấu trên TXĐ thì hàm không có cực trị.
Xét phương án
A.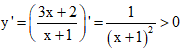 
nên hàm số không có cực trị
Suy ra câu A sai.
B.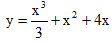 
có đạo hàm: y'= x2 + 2x + 4 = (x + 1)2 + 3 > 0 mọi x nên y là không có cực trị là câu chính xác.
C. y' = 4x3 + 12x = 4x(x2 + 3); y' = 0 ⇔ x = 0
y'' = 12x2 + 12; y''(0) = 12 > 0
⇒ x = 0 là điểm cực tiểu
D. Đây là câu lí thuyết.
Suy ra chọn đáp án A.
Câu 5: Cực trị của hàm số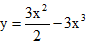 
là:
A. xCD = 0, xCT = 1/3 B. xCD = 3, xCT = -3
C. xCD = 1/3, xCT = 0 D. Không có cực trị.
- TXĐP: D = R. Ta có:
y' = 3x - 9x2 = 3x(1 - 3x); y' = 0 
y'' = 3 - 18x; y''(0) = 3 > 0; y'(1/3) = -3 < 0
⇒ xCD = 1/3, xCT = 0
Kết luận: hàm số đạt cực trị với xCD = 1/3, xCT = 0
Suy ra chọn đáp án C.
Câu 6: Hàm số y = ax4 + bx2 + c với a ≠ 0 có tối đa bao nhiêu cực trị?
A. 1 B. 2
C. 3 D. 4
Đạo hàm: y' = 4ax3+ 2bx là hàm bậc ba.
Phương trình bậc 3: y' = 0 có tối đa 3 nghiệm. Vậy số điểm cực trị tối đa là 3.
Suy ra chọn đáp án C.
Câu 7: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.
+ Do hàm số xác định tại x = 0 và đạo hàm đổi dấu từ dương sang âm khi x qua x = 0 nên hàm số đạt cực đại tại x = 0 .
+ Do hàm số xác định tại x = 1; y'(1) = 0 và đạo hàm đổi dấu từ âm sang dương khi x qua x = 1 nên hàm số đạt cực tiểu tại x = 1 .
Suy ra chọn đáp án D.
Câu 8: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.
+ Do hàm số xác định tại x = 1, y'(1) = 0 và đạo hàm đổi dấu từ âm sang dương khi x đi qua x = 1 nên hàm số đạt cực tiểu tại x = 1; giá trị cực tiểu là y(1) = -1.
+ Tại x = 0 hàm số không xác định nên x= 0 không là điểm cực trị củ hàm số.
+ Hàm số không có giá trị lớn nhất; giá trị nhỏ nhất.
Suy ra chọn đáp án A.
Câu 9: Cho hàm số y = f(x) liên tục tại x0 và có bảng biến thiên
Khi đó hàm số đã cho có:
A. Hai điểm cực đại, một điểm cực tiểu.
B. Một điểm cực đại, không có điểm cực tiểu.
C. Một điểm cực đại, hai điểm cực tiểu.
D. Một điểm cực đại, một điểm cực tiểu.
+ Hàm số không có đạo hàm tại x0 nhưng hàm số vẫn liên tục tại x0 thì hàm số vẫn đạt cực trị tại x0.
+ Trong trường hợp này; hàm số đạt cực đại tại điểm x1 và đạt cực tiểu tại x0.
Do đó đáp án D đúng.
Suy ra chọn đáp án D.
Câu 10: Cho hàm số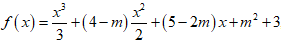 
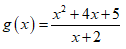
với m là tham số thực. Hàm số 
có đồ thị (C) và bảng biến thiên sau:
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1?
A. m > 2 B. 
C. m < -5/2 D. m > 5/2
Ta có: f'(x)= x2 + (4 - m)x + 5 - 2m
Xét phương trình: f'(x) = x2 + (4 - m)x + 5 – 2m = 0
⇒ x2 + 4x + 5 = m(x + 2) 
Ta có nghiệm của f'(x) = 0 cũng là hoành độ giao điểm của phương trình g(x) = m
Khi đó từ bảng biến thiên, để hàm số đạt cực trị tại ít nhất tại 1 điểm mà điểm đó lớn hơn – 1 khi và chỉ khi m > 2.
Suy ra chọn đáp án A.
Câu 11: Cho hàm số y = f(x) có f'(x) = x(x-1)2.(x + 1)3, hỏi số điểm cực trị của hàm số y = f(x).
A. 1 B. 2
C. 3 D. 4
f'(x) = 0 ⇔ x(x-1)2.(x + 1)3 = 0 
Do x = 1 là nghiệm kép nên không là điểm cực trị của hàm số.
Do x = 0 là nghiệm đơn nên là điểm cực trị của hàm số.
Do x = -1 là nghiệm bội lẻ nên là điểm cực trị của hàm số.
Vậy hàm số đã cho có 2 điểm cực trị.
Suy ra chọn đáp án B.
Câu 12: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:
Số điểm cực trị của hàm số f(x) trên K là:
A. 1 B. 2
C. 3 D. 4
Dựa vào đồ thị ta thấy phương trình f'(x) = 0 chỉ có một nghiệm đơn (tại x = -1) và hai nghiệm kép (tại x = 0 và x = 2).
Suy ra f'(x) chỉ đổi dấu khi qua nghiệm đơn này. Do đó, hàm số f(x) có đúng một cực trị.
Suy ra chọn đáp án A.
Câu 13: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:
Số điểm cực trị của hàm số y= f(x) + 2018 trên K là:
A. 1 B. 2
C. 3 D.4
+ Dựa vào đồ thị ta thấy phương trình f'(x) = 0 có ba nghiệm đơn (đồ thị hàm số y = f'(x) = 0 cắt trục hoành tại 3 điểm phân biệt) nên y' đổi dấu khi qua nghiệm đơn này.
+ Lại có: y = f(x) + 2018 có y'= f'(x). Do đó suy ra hàm số y= f(x) + 2018 có ba điểm cực trị.
Suy ra chọn đáp án C.
Câu 14: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:
Số điểm cực trị của hàm số y= f(x) + 2x trên K là:
A. 0 B. 1
C. 2 D. 3
Hàm số y= f(x) + 2x có đạo hàm y'= f'(x) + 2
Phương trình y’= 0 ⇔ f'(x) = -2
Số nghiệm của phương trình y' = 0 là số giao điểm của đồ thị hàm số y = f'(x) và đường thẳng y = - 2
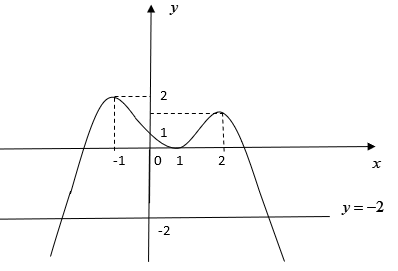
Dựa vào đồ thị ta thấy phương trình y'= 0 có hai nghiệm và y' không đổi dấu khi qua các nghiệm này. Do đó suy ra hàm số y = f(x) + 2x không có cực trị.
Suy ra chọn đáp án A.
Câu 15: Hàm số f(x) có đạo hàm f’(x) trên R. Cho đồ thị của hàm số f’(x) như sau:
Số điểm cực trị của hàm số y = f(x2) là:
A. 1 B. 2
C. 3 D. 4
Ta có: y = f(x2) nên y'= 2x. f'(x2)
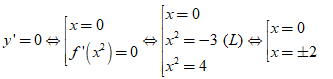
Dấu y':
Do đó suy ra hàm số y= f(x2) có ba điểm cực trị.
Suy ra chọn đáp án C.
Câu 16: Hàm số y = f(x) có đồ thị như hình bên dưới. Hỏi đồ thị hàm số có mấy điểm cực trị:
A. 3. B. 2.
C. 1. D. 0.
Căn cứ vào sự đi lên đi xuống của đồ thị ta thấy hàm số có 3 điểm cực trị.
Suy ra chọn đáp án A.
Câu 17: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ:
Số điểm cực trị của hàm số y = |f(x)| là:
A. 3 B. 4
C. 7 D. 0
Từ đồ thị hàm số y = f(x) ta suy ra đồ thị hàm số y = |f(x) |.
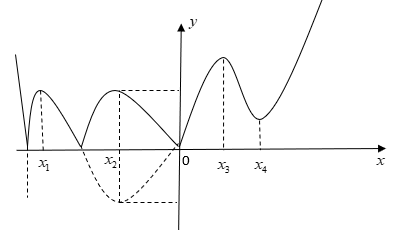
Dựa vào đồ thị hàm số suy ra hàm số y = |f(x)| có 7 điểm cực trị.
Suy ra chọn đáp án C.
Câu 18: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ sau. Số điểm cực trị của hàm số y = f(|x|) là:
A. 0 B. 2
C. 4 D. 5
Từ đồ thị hàm số y = f(x) ta suy ra đồ thị hàm số y = f(|x|).
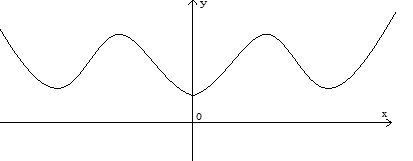
Từ đồ thị hàm số y= f(|x|); suy ra hàm số có 5 điểm cực trị.
Suy ra chọn đáp án D.
Câu 19: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) có đồ thị như hình vẽ sau. Số điểm cực trị của hàm số y = |2f(x) – 3| là:
A. 3 B. 5
C. 7 D. 9
Từ đồ thị hàm số y= f(x) ta suy ra đồ thị hàm số y = |2f(x) - 3|
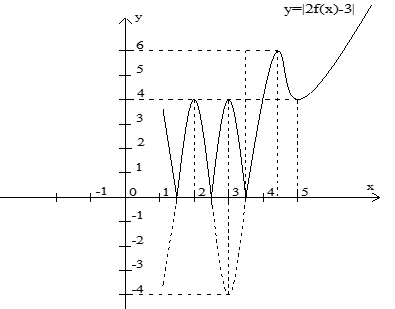
Suy ra đồ thị hàm số y = |2f(x) - 3| có 7 điểm cực trị.
Suy ra chọn đáp án C.
Câu 20: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ:
Số điểm cực trị của hàm số y = |[f(x)]2 - 1| là:
A. 7 B. 9
C. 11 D. 13
Đặt u(x) = f2(x) – 1
Đạo hàm: u'(x) = 2f(x).f'(x)
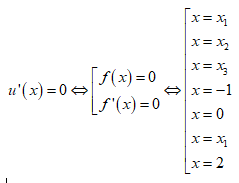
Phương trình u'(x) = 0 có các nghiệm đơn.
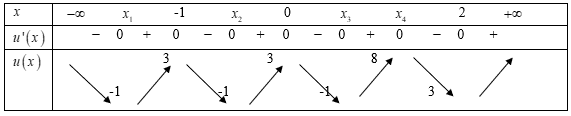
Suy ra đồ thị hàm số y = |[f(x)]2 - 1|
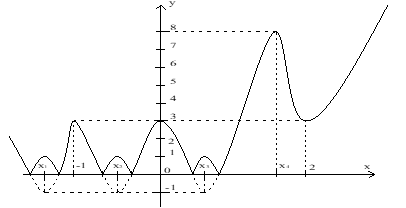
Đồ thị hàm số y = |[f(x)]2 - 1| có 13 điểm cực trị.
Suy ra chọn đáp án D.
Câu 21: Hàm số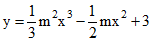 
với m ≠ 0 đạt cực đại tại x = -4/5 với giá trị của m nào dưới đây ?
A. m = 0 B. m = -13/5
C. m = -5/4 D. m = 2/3
Hàm số đạt giá trị cực đại tại x khi y'(x) = 0 và y''(x) < 0
Ta có: y'(x) = m2.x2 – 2mx và y'' = 2m2x – 2m
- Hàm số đạt cực đại tại x = -4/5 khi
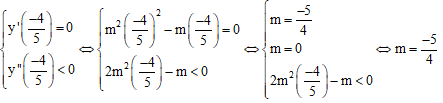
Suy ra chọn đáp án C.
Câu 22: Tìm giá trị cực đại yCĐ của hàm số y = x3 – 3x + 2
A. yCĐ = 4 B. yCĐ = 1
C. yCĐ = 0 D. yCĐ = -1
Đạo hàm: y'= 3x2 – 3
Xét phương trình y' = 0 ⇔ 3x2 – 3 = 0 ⇔ x = 1 hoặc x = -1.
Ta có y'' = 6x.
Do y''(1)= 6 > 0 nên điểm x = 1 là điểm cực tiểu của hàm số.
Do y''(-1)= -6 < 0 nên điểm x = -1 là điểm cực đại của hàm số
⇒ Giá trị cực đại là: yCĐ = y(-1) = 4.
Suy ra chọn đáp án A.
Câu 23: Cho hàm số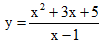 
có 2 cực trị x1, x2. Tính S = x1 + x2.
A. S = 2 B. S = -2
C. S = 2√3 D. S = -2√3
TXĐ: D = R\{1}
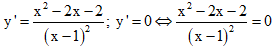
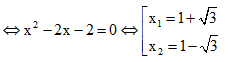
Vậy S = x1 + x2 = 2.
Suy ra chọn đáp án A.
Câu 24: Tìm m để hàm số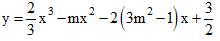 
có 2 cực trị x1, x2 thỏa mãn x1.x2 + 2.(x1 + x2) = 1
A. m = 2/√3 B. m = 3/√2
C. m = 2/3 D. Đáp án khác
Đạo hàm: y' = 2x2 – 2mx – 2(3m2 - 1)
Xét phương trình y' = 0 ⇔ x2 – mx – 3m2 + 1 = 0
Để hàm số có 2 điểm cực trị
⇔ Δ = b2 - 4ac = 13m2 - 4 > 0 
Khi đó: x1.x2 + 2(x1 + x2) = 1 ⇔ -3m2 + 1 + 2m = 1 
Vậy m = 2/3 thỏa điều kiện đặt ra.
Suy ra chọn đáp án C.
Câu 25: Cho hàm số y= -x4 + (5m - 1)x2 + 2. Hàm số đã cho có đúng 1 cực trị với giá trị nào của m sau đây ?
A. m ≥ 1/5 B. m > 1/5
C. m < 1/5 D. m ≤ 1/5
y' = -4x3 + 2(5m - 1)x; y' = 0 
Để hàm số có đúng 1 cực trị 
Suy ra chọn đáp án D.
Câu 26: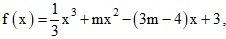 
, với giá trị nào của m thì hàm số có cực tiểu, cực đại
A. 4 ≤ m ≤ 1 B. -4 ≤ m ≤ 1
C. m < -4 hoặc m > 1 D. m ≤ -4 hoặc m ≥ 1
Đạo hàm: f'(x) = x2 + 2mx – 3m + 4
Xét phương trình: f'(x) = 0 hay x2 + 2mx – 3m + 4 =0
Hàm số đã cho có cực đại và cực tiểu khi và chỉ khi f'(x) = 0 có 2 nghiệm phân biệt.
Δ' = m2 + 3m - 4 > 0 
Suy ra chọn đáp án C.
Câu 27: Hàm số y = ax3 + bx2 + cx + d với a ≠ 0 có 2 cực trị khi nào ?
A. y' = 0 có nghiệm.
B. y' = 0 có 2 nghiệm phân biệt.
C. y' = 0 có 2 nghiệm trái dấu.
D. Hàm số luôn có 2 cực trị.
Hàm số bậc ba y = ax3 + bx2 + cx + d với a ≠ 0 có đạo hàm y' = 3ax2 + 2bx + c (*)
Để hàm số đã cho có hai điểm cực trị khi và chỉ khi y' = 0 có 2 nghiệm phân biệt.
Suy ra chọn đáp án B.
Câu 28: Cho hàm số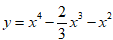 
. Mệnh đề nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu là 0.
B. Hàm số có hai giá trị cực tiểu là -2/3 và -5/48.
C. Hàm số chỉ có một giá trị cực tiểu.
D. Hàm số có giá trị cực tiểu là -2/3 và giá trị cực đại là -5/48.
TXĐ: D = R và có đạo hàm y' = 4x3 – 2x2 – 2x = 2x(2x2 – x – 1)
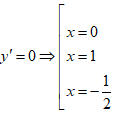
Bảng biến thiên
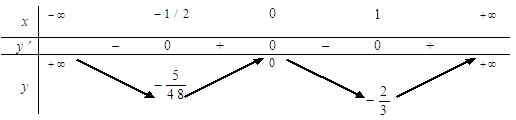
Dựa vào bảng biến thiên ta có đáp án B.
Suy ra chọn đáp án B.
Câu 29: Tọa độ điểm cực đại của hàm số y = x3 – 3x2 + 4 là:
A. (2;4) B. (2; 0)
C. (0;- 4) D. (0 ; 4)
Tập xác định: D= R.
Đạo hàm y’= 3x2 – 6x
Xét phương trình: y' = 0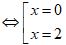 
; y'' = 6x - 6
Ta có: y''(0) = - 6 < 0 nên điểm cực đại của hàm số là x = 0 và yCĐ = 4.
Do y''( 2) = 6 > 0 nên điểm x = 2 là điểm cực tiểu của hàm số và yCT = 0 .
Vậy điểm cực đại của đồ thị hàm số là (0; 4)
Suy ra chọn đáp án D.
Câu 30: Cho hàm số y = x3 – 3x2 +1 (C). Đường thẳng đi qua điểm A(- 1; 1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) có phương trình là
A. y = - x B. x - 4y + 5 = 0
C. y = 2x + 3 D. x - 2y + 3 = 0
Cách 1: TXĐ: D = R.
Đạo hàm y'= 3x2 – 6x
Ta có: y = 1/3. (x + 1).y' + (-2x + 1).
Suy ra; đường thẳng đi qua 2 điểm cực trị là Δ: y = -2x + 1
Đường thẳng d vuông góc Δ có dạng d: y = 1/2.x + b
Do A(-1;1) ∈ d ⇒ 1 = -1/2 + b ⇒ b = 3/2.
Vậy đường thẳng d cần tìm là y = 1/2.x + 3/2 hay d: x – 2y + 3 = 0
Cách 2: Ta có: y'= 3x2 - 6x
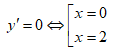
Tọa độ hai điểm cực trị: B(0; 1) và C(2; -3)
Hệ số góc của đường thẳng BC là: 
⇒ Hệ số góc của đường thẳng cần tìm kd = 1/2
(Vì đường thẳng cần tìm vuông góc với đường thẳng tạo bởi hai điểm cực trị nên kBC. kd = -1)
Phương trình đường thẳng d: y = 1/2.(x + 1) + 1 ⇔ x – 2y + 3 = 0.
Suy ra chọn đáp án D.
Câu 31: Cho hàm số y = x3 – 3x có giá trị cực đại và cực tiểu lần lượt là y1; y2. Khi đó:
A. y1 + y2 = 1 B. 2y1 – y2 = 4
C. 2y2 + y1 = 2 D. y1 - y2 = 4
Ta có: y' = 3x2 - 3 = 0 
Do y'' = 6x; y''(1) = 6 > 0 nên điểm x = 1 là điểm cực tiểu của hàm số
Vì y''(-1)= -6 < 0 nên điểm x = -1 là điểm cực đại của hàm số.
Suy ra y1 = y(-1) = 2; y2 = y(1) = -2
Vậy y1 – y2 = 4.
Suy ra chọn đáp án D.
Câu 32: Đồ thị của hàm số y = 3x4 – 4x3 – 6x2 + 12x + 1 đạt cực tiểu tại M(x1; y1). Tính tổng S = x1 + y1
A. 5 B. - 11
C. 7 D. 6
Đạo hàm y' = 12x3 – 12x2 – 12x + 12
y' = 0 ⇔ x3 - x2 - x + 1 = 0 ⇔ (x + 1)(x - 1)2 = 0 
Lập bảng biến thiên, ta thu được điểm cực tiểu là M(-1; -10)
Do đó tổng S = x1 + y1 = -11
Suy ra chọn đáp án B.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
