Cấp số cộng là gì? Công thức tính Cấp số cộng và bài tập ví dụ

Quý Lê Xuân Ngày: 08-03-2024 Tổng hợp kiến thức

Tải xuống 6 5.2 K 5

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ tài liệu về Cấp số cộng, tài liệu bao gồm có đầy đủ lý thuyết, tính chất, công thức tính tổng cấp số cộng và các dạng bài tập về cấp số cộng, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Cấp số cộng là gì? Công thức tính Cấp số cộng và bài tập ví dụ

1. Định nghĩa Cấp số cộng

Dãy số $u_{n}$ là một cấp số cộng nếu $u_{n + 1} = u_{n} + d$ với mọi $n \in N^{*}$ , $d$ là hằng số.

$d = u_{n + 1} - u_{n}$ được gọi là công sai.

* $d = 0$ : CSC là một dãy số không đổi.

Ví dụ:

Dãy số $3; 6; 9; 12; 15$ là một cấp số cộng vì:

$\begin{array}{l} 6 = 3 + 3 \\ 9 = 6 + 3 \\ 12 = 9 + 3 \\ 15 = 12 + 3 \end{array}$

Đây là CSC có công sai $d = 3$ và số hạng đầu $u_{1} = 3$ .

2. Số hạng tổng quát của Cấp số cộng

Kí hiệu: $u_{n} = u_{1} + (n - 1) d, (n \geq 2)$ . ( n là số tự nhiên bất kì lớn hơn 1)

Như vậy công sai còn có thể tính bởi công thức: $d = \frac{u_{n} - u_{1}}{n - 1}$ .

Ví dụ:

Cho CSC $(u_{n})$ biết $u_{1} = - 1, d = 3$ . Tìm $u_{20}$ .

Ta có:

$\begin{array}{l} u_{20} = u_{1} + (20 - 1) d \\ = u_{1} + 19 d \\ = - 1 + 19.3 \\ = 56 \end{array}$

3. Tính chất của Cấp số cộng

$u_{k} = \frac{u_{k - 1} + u_{k + 1}}{2}$ với $k \geq 2$ hay $u_{k + 1} + u_{k - 1} = 2 u_{k}$

Ví dụ:

Cho ba số $3; x; 9$ theo thứ đó lập thành một CSC. Tìm $x .$

Ta có: $x = \frac{3 + 9}{2} = 6$ .

Vậy $x = 6$ .

4. Tổng n số hạng đầu của Cấp số cộng

+) Thông qua số hạng đầu, cuối và số số hạng: $S_{n} = \frac{n (u_{1} + u_{n})}{2}$ , với $n \in N^{*}$

+) Thông qua số hạng đầu, số số hạng và công sai:

$S_{n} = n u_{1} + \frac{n (n - 1)}{2} d$

$S_{n} = \frac{n [2 u_{1} + (n - 1) d]}{2}$

Ví dụ:

Cho CSC $(u_{n})$ thỏa mãn $u_{1} = - 1, d = 3$ . Tính $S_{20} .$

Ta có:

$\begin{array}{l} S_{20} = 20 u_{1} + \frac{20. (20 - 1)}{2} . d \\ = 20. (- 1) + \frac{20.19}{2} .3 \\ = 550 \end{array}$

5. Các dạng bài tập về Cấp số cộng và ví dụ minh họa

Dạng 1. Xác định cấp số cộng và các yếu tố của cấp số cộng

Phương pháp giải:

- Dãy số (u_n) là một cấp số cộng khi và chỉ khi u_{n + 1} – u_n = d không phụ thuộc vào n và d là công sai của cấp số cộng đó.

- Để xác định một cấp số cộng, ta cần xác định số hạng đầu và công sai. Ta thiết lập một hệ phương trình hai ẩn u₁ và d. Tìm u₁ và d.

- Tìm số hạng thứ n dựa vào công thức tổng quát: u_n = u₁ + (n – 1)d hoặc công thức truy hồi u_n = u_{n - 1} + d.

Ví dụ minh họa:

Ví dụ 1: Cho các dãy số sau, dãy số nào là cấp số cộng. Nếu là cấp số cộng hãy xác định số hạng đầu tiên và công sai:

a) – 2; 1; 4; 7; 10; 13; 16; 19.

b) 2; 4; 6; 10; 12; 14; 16; 18; 20.

c) Dãy số (a_n), với a_n = 4n – 3.

Lời giải

a) Ta thấy 1 – (– 2) = 4 – 1 = 7 – 4 = 10 – 7 = 13 – 10 = 16 – 13 = 19 – 16 = 3

Nên dãy số – 2; 1; 4; 7; 10; 13; 16; 19 là cấp số cộng.

Số hạng đầu tiên của cấp số cộng là u₁ = – 2, công sai là d = 3.

b) Ta thấy: 4 – 2 = 2 nhưng 10 – 6 = 4

Nên dãy số 2; 4; 6; 10; 12; 14; 16; 18; 20 không là cấp số cộng.

c) Ta có: a_n = 4n – 3 thì a_n₊₁ = 4(n + 1) – 3.

Xét a_n₊₁ – a_n = 4(n + 1) – 3 – (4n – 3) = 4 (không đổi)

Vậy dãy số (a_n) với a_n = 4n – 3 là cấp số cộng.

Số hạng đầu tiên của cấp số cộng là a₁ = 4.1 – 3 = 1, công sai là d = 4.

Ví dụ 2: Cho cấp số cộng (u_n) thỏa mãn: 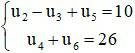Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

a) Xác định công sai và hạng đầu tiên của cấp số cộng trên.

b) Xác định công thức tổng quát của cấp số cộng trên.

c) Tìm số hạng thứ 15 của cấp số cộng trên.

d) Số 6061 là số hạng thứ bao nhiêu của cấp số cộng.

Lời giải

Gọi cấp số cộng có số hạng đầu tiên là u₁ và công sai d

Số hạng tổng quát của (u_n) là u_n = u₁ + (n – 1)d

Ta có: 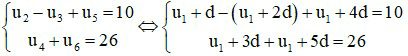Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Vậy u₁ = 1 và d = 3.

b) Số hạng tổng quát là: u_n = 1 + (n – 1).3 hay u_n= 3n – 2 với n ∈ ℕ^∗.

c) Số hạng thứ 15 của cấp số cộng: u₁₅= 3.15 – 2 = 43.

d) Giả sử số hạng thứ k của cấp số cộng là u_k = 6061, ta có: u_k = 3k – 2 = 6061, suy ra k = 2021.

Vậy số 6061 là số hạng thứ 2021 của cấp số cộng.

Dạng 2. Tìm điều kiện để dãy số lập thành cấp số cộng. Chứng minh cấp số cộng

Phương pháp giải:

Sử dụng tính chất: Ba số hạng u_k-1; u_k; u_k+1 là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi 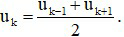Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 .

Ví dụ minh họa:

Ví dụ 1:

a) Tìm x biết: x² + 1, x – 2, 1 – 3x lập thành cấp số cộng.

b) Cho cấp số cộng – 2, x, 6, y. Tính giá trị của biểu thức P = x² + y².

Lời giải

a) Ta có: x² + 1, x – 2, 1 – 3x lập thành cấp số cộng

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Vậy x = 2, x = 3 là những giá trị cần tìm.

b) Theo tính chất của cấp số cộng, ta có 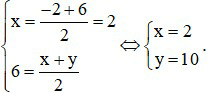Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 .

Vậy P = x² + y² = 2² + 10² = 104.

Ví dụ 2: Chứng minh rằng:

a) Nếu ba số a, b, c lập thành một cấp số cộng thì ba số x, y, z cũng lập thành một cấp số cộng, với: x = a² – bc, y = b² – ca, z = c² – ab.

b) Nếu phương trình x³ – ax² + bx – c = 0 có ba nghiệm lập thành cấp số cộng thì 9ab = 2a³ + 27c.

Lời giải

a) a, b, c là cấp số cộng nên a + c = 2b

Cần chứng minh x, y, z cũng lập thành một cấp số cộng tức là x + z = 2y.

Ta có 2y = 2b² – 2ca

Và x + z = a²+ c² - b(a + c)

= (a + c)²– 2ac – 2b²

= 4b² – 2ac – 2b²

= 2b² – 2ac = 2y

Khi đó ta được: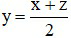 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Vậy ta có điều phải chứng minh.

b) Giả sử phương trình có ba nghiệm x₁, x₂, x₃ lập thành cấp số cộng khi đó: x₁ + x₃ = 2x₂ (1)

Mặt khác: x³ – ax² + bx – c = (x – x₁)(x – x₂)(x – x₃)

= x³ – (x₁ + x₂ + x₃)x² + (x₁ x₂ + x₂ x₃ + x₃ x₁)x – x₁ x₂ x₃

Suy ra x₁ + x₂ + x₃ = a (2)

Từ (1) và (2), ta được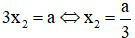 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Vì phương trình đã cho có nghiệm 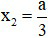Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 , tức là:

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Vậy ta có điều phải chứng minh.

Dạng 3. Tính tổng của một cấp số cộng

Phương pháp giải:

Tổng n số hạng đầu tiên S_nđược xác định bởi công thức:

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Ví dụ minh họa:

Ví dụ 1: Cho cấp số cộng (u_n)

a) (u_n) có số hạng tổng quát là: u_n = 7n – 3. Tính S₁₀₀.

b) (u_n) có u₂ + u₂₂= 40. Tính S_23.

c) (u_n) có u₄+ u₈ + u₁₂+ u₁₆= 224. Tính S₁₉.

Lời giải

a) Từ công thức số hạng tổng quát

Ta có:

Số hạng đầu: u₁ = 7 . 1 – 3 = 4;

Số hạng thứ hai là : u₂ = 7 . 2 – 3 = 11;

Công sai: d = 11 – 4 = 7

Khi đó ta có:

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

b) Ta có: u₂ + u₂₂ = 40 ⇔ u₁ + d + u₁ +21d = 40 ⇔ 2u₁ + 22d = 40

Vậy 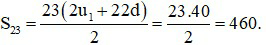Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

c) Ta có: u₄ + u₈+ u₁₂ + u₁₆ = 224

⇔ u₁ + 3d + u₁ +7d + u₁ +15d = 224

⇔ 4u₁ + 36d = 224

⇔ u₁ + 9d = 56

Vậy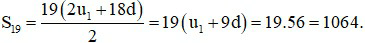 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Ví dụ 2: Tính các tổng sau:

a) S = 1 + 3 + 5 +... + (2n – 1) + (2n + 1)

b) S = 1 + 4 + 7 +... + (3n – 2) + (3n + 1) + (3n + 4)

c) S = 100² – 99² + 98²– 97² +... + 2² – 1²

Lời giải

a) Ta có dãy số 1;3;5;...;(2n – 1);(2n + 1) là cấp số cộng với công sai d = 2 và u₁= 1, số hạng tổng quát u_k = u₁ + (k – 1)d.

Ta kiểm tra 2n + 1 là số hạng thứ bao nhiêu của dãy: 2n + 1 = u₁ + (k – 1)d

⇔ 2n + 1 = 1 + (k – 1).2 ⇒ k = n + 1 . Do đó dãy số có n + 1 số hạng.

Vậy Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

b) Ta có dãy số 1; 4; 7; ... (3n – 2);(3n + 1);(3n + 4) là cấp số cộng với công sai d = 3 và u₁ = 1, số hạng tổng quát u_k = u₁+ (k – 1)d.

Ta kiểm tra 2n + 1 là số hạng thứ bao nhiêu của dãy: 3n + 4 = u₁+ (k – 1)d

⇔ 3n + 4 = 1 + (k – 1).3 ⇒ k = n + 2. Do đó dãy số có n + 2 số hạng.

Vậy 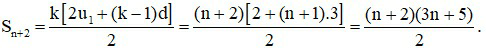Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

c) S = 100² – 99²+ 98² – 97²+... + 2²– 1²

= (100 – 99)(100 + 99) + (98 – 97)(98 + 97) +... + (2 – 1)(2 + 1)

= 199 + 195 +... + 3

= 3 + 7 +... + 195 + 199

Ta có dãy số 3; 7; ...195; 199 là cấp số cộng với công sai d = 4, số hạng đầu tiên u₁ = 3 và số hạng thứ n là u_n = 199.

Do đó có 199 = 3 + (n – 1).4 ⇒ n + 50.

Vậy 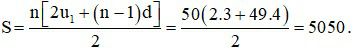Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 .

6. Bài tập tự luyện

Câu 1. Trong các dãy số dưới đây, dãy số nào là cấp số cộng?

A. Dãy số (a_n), với a_n = 2ⁿ ,∀n ∈ ℕ^∗.

B. Dãy số (b_n), với b₁ = 1,b_n+1 = 2b₁ + 1,∀n ∈ ℕ^∗.

C. Dãy số (c_n), với c_n = (2n – 3)² – 4n² ,∀n ∈ ℕ^∗.

D. Dãy số (d_n), với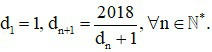 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Câu 2. Trong các dãy số (u_n) sau, dãy số nào là một cấp số cộng?

A. 1; – 3; – 7; – 11; – 15

B. 1; – 3; – 6; – 9; – 12

C. 1; – 2; – 4; – 6; – 8

D. 1; – 3; – 5; – 7; – 9

Câu 3. Trong các dãy số (u_n) cho bởi số hạng tổng quát u_n sau, dãy số nào không phải là một cấp số cộng?

Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Câu 4. Cho cấp số cộng (u_n), biết u₁ = – 5,d = 3. Khẳng định nào sau đây là đúng?

A. u₁₅ = 34.

B. u₁₅ = 45.

C. u₁₃ = 31.

D. u₁₀ = 35.

Câu 5. Cho cấp số cộng (u_n), biết u₁ = – 5; d = 3. Số 100 là số hạng thứ bao nhiêu?

A. Số thứ 15.

B. Số thứ 20.

C. Số thứ 35.

D. Số thứ 36.

Câu 6. Cho cấp số cộng (u_n) biết: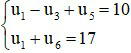 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 . Số hạng đầu tiên là

A. u₁ = 16.

B. u₁ = 6.

C. u₁ = 7.

D. u₁ = 14.

Câu 7. Cho cấp số cộng (u_n) thỏa: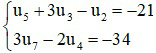 Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11 . Tính số hạng thứ 100 của cấp số.

A. u₁₀₀ = – 243

B. u₁₀₀ = – 295

C. u₁₀₀ = – 231

D. u₁₀₀ = – 294

Câu 8. Cho cấp số cộng (u_n) có u₁ = 123 và u₃– u₁₅= 84. Tìm số hạng u₁₇.

A. u₁₇ = 242

B. u₁₇ = 235

C. u₁₇ = 11

D. u₁₇ = 4

Câu 9. Xác định x để 3 số 1 – x; x²; 1 + x lập thành một cấp số cộng.

A. x = 1 hoặc x = – 1

B. x = 2 hoặc x = – 2

C. Không có giá trị nào của x.

D. x = 0

Câu 10. Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. a² + c² = 2ab + 2bc.

B. a² – c² = 2ab – 2bc.

C. a² + c²= 2ab – 2bc.

D. a² – c² = ab – bc.

Câu 11. Cho cấp số cộng (u_n) có u₁ = 5 và d = – 4. Tính tổng của 100 số hạng đầu tiên.

A. – 19500

B. – 19300

C. – 19750

D. – 19550

Câu 12. Cho dãy số (u_n) xác định bởi u₁ = 321 và u_{n + 1}= u_n – 3 với mọi n ∈ ℕ^∗. Tính tổng S của 125 số hạng đầu tiên của dãy số đó.

A. S = 16875.

B. S = 63375.

C. S = 63562,5.

D. S = 16687,5.

Câu 13. Số hạng tổng quát của một cấp số cộng là u_n = 3n + 4 với n ∈ ℕ^∗. Gọi S_n là tổng n số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào sau đây đúng?

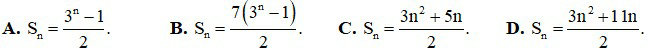
Các dạng toán về Cấp số cộng và cách giải hay, chi tiết | Toán lớp 11

Câu 14. Cho cấp số cộng 3; 8; 13;... Tính tổng S = 3 + 8 + 13 +... + 2018.

A. S = 408422.

B. S = 408242.

C. S = 407231,5.

D. S = 409252,5.

Câu 15. Phương trình x³ – 3x² – 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.

A. m = 16

B. m = 11

C. m = 13

D. m = 12

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
C	A	B	C	C	A	B	C	A	B	B	A	D	B	B

Câu 16: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. $a^{2} + c^{2} = 2 a b + 2 b c$ .

B. $a^{2} - c^{2} = 2 a b - 2 b c$ .

C. $a^{2} + c^{2} = 2 a b - 2 b c$ .

D. $a^{2} - c^{2} = a b - b c$ .

Hướng dẫn giải:

Chọn B.

a, b, c theo thứ tự lập thành cấp số cộng khi và chỉ khi:

$b - a = c - b \Leftrightarrow {(b - a)}^{2} = {(c - b)}^{2} \Leftrightarrow a^{2} - c^{2} = 2 a b - 2 b c$ .

Suy ra chọn đáp án B.

Câu 17: Cho $a, b, c$ theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. $a^{2} + c^{2} = 2 a b + 2 b c + 2 a c$ .

B. $a^{2} - c^{2} = 2 a b + 2 b c - 2 a c$ .

C. $a^{2} + c^{2} = 2 a b + 2 b c - 2 a c$ .

D. $a^{2} - c^{2} = 2 a b - 2 b c + 2 a c$ .

Hướng dẫn giải:

Chọn C.

$a, b, c$ theo thứ tự lập thành cấp số cộng khi và chỉ khi

$b - a = c - b \Leftrightarrow {(b - a)}^{2} = {(c - b)}^{2} \Leftrightarrow a^{2} - c^{2} = 2 a b - 2 b c$

$\begin{array}{l} \Leftrightarrow a^{2} + c^{2} = 2 c^{2} + 2 a b - 2 b c = 2 a b + 2 c (c - b) \\ = 2 a b + 2 c (b - a) = 2 a b + 2 b c - 2 a c \end{array}$

Câu 18: Cho $a, b, c$ theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?

A. $2 b^{2}, a, c^{2}$ .

B. $- 2 b, - 2 a, - 2 c$ .

C. $2 b, a, c$ .

D. $2 b, - a, - c$ .

Hướng dẫn giải:

Chọn B.

Ta có $a, b, c$ theo thứ tự lập thành cấp số cộng khi và chỉ khi $a + c = 2 b$

$\Leftrightarrow - 2 (b + c) = - 2.2 a \Leftrightarrow (- 2 b) + (- 2 c) = 2 (- 2 a)$

$\Leftrightarrow - 2 b, - 2 a, - 2 c$ lập thành một cấp số cộng

Câu 19: Xác định $x$ để 3 số : $1 - x; x^{2}; 1 + x$ theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của $x$ .

B. $x = \pm 2$ .

C. $x = \pm 1$ .

D. $x = 0$ .

Hướng dẫn giải: :

Chọn C.

Ba số : $1 - x; x^{2}; 1 + x$ lập thành một cấp số cộng khi và chỉ khi $x^{2} - (1 - x) = 1 + x - x^{2}$

$\Leftrightarrow 2 x^{2} = 2 \Leftrightarrow x = \pm 1$ suy ra chọn đáp án C.

Câu 20: Xác định để 3 số : $1 + 2 x; 2 x^{2} - 1; - 2 x$ theo thứ tự lập thành một cấp số cộng?

A. $x = \pm 3$ .

B. $x = \pm \frac{\sqrt{3}}{2}$ .

C. $x = \pm \frac{\sqrt{3}}{4}$ .

D. Không có giá trị nào của $x$ .

Hướng dẫn giải:

Chọn B.

Ba số : $1 + 2 x; 2 x^{2} - 1; - 2 x$ theo thứ tự lập thành một cấp số cộng khi và chỉ khi

$2 x^{2} - 1 - 1 - 2 x = - 2 x - 2 x^{2} + 1$

$\Leftrightarrow 4 x^{2} = 3 \Leftrightarrow x = \pm \frac{\sqrt{3}}{2}$ . Suy ra chọn đáp án B.

Câu 21: Xác định $a$ để 3 số : $1 + 3 a; a^{2} + 5; 1 - a$ theo thứ tự lập thành một cấp số cộng?

A. Không có giá trị nào của $a$ .

B. $a = \pm 1$ .

C. $a = \pm 1$

D. $a = \pm 1$ .

Hướng dẫn giải:

Chọn A.

Ba số : $1 + 3 a; a^{2} + 5; 1 - a$ theo thứ tự lập thành một cấp số cộng khi và chỉ khi

$a^{2} + 5 - (1 + 3 a) = 1 - a - (a^{2} + 5)$

$\Leftrightarrow a^{2} - 3 a + 4 = - a^{2} - a - 4$ . PT vô nghiệm

Suy ra chọn đáp án A.

Câu 22: Tìm $x$ biết :

$x^{2} + 1, x - 2, 1 - 3 x$ lập thành cấp số cộng ;

A. $x = 4, x = 3$

B. $x = 2, x = 3$

C. $x = 2, x = 5$

D. $x = 2, x = 1$

Hướng dẫn giải:

Chọn B.

Ta có: $x^{2} + 1, x - 2, 1 - 3 x$ lập thành cấp số cộng

$\Leftrightarrow x^{2} + 1 + 1 - 3 x = 2 (x - 2) \Leftrightarrow x^{2} - 5 x + 6 = 0 \Leftrightarrow x = 2; x = 3$

Vậy $x = 2, x = 3$ là những giá trị cần tìm.

Câu 23: Cho các số $5 x - y, 2 x + 3 y, x + 2 y$ lập thành cấp số cộng ; các số ${(y + 1)}^{2}, x y + 1, {(x - 1)}^{2}$ lập thành cấp số nhân.Tính $x, y$

A. $(x; y) = (0; 0); (\frac{1}{3}; \frac{4}{3}); (- \frac{3}{4}; - \frac{3}{10})$

B. $(x; y) = (0; 0); (\frac{10}{3}; \frac{4}{3}); (- \frac{3}{4}; - \frac{3}{10})$

C. $(x; y) = (1; 0); (\frac{11}{3}; \frac{4}{3}); (- \frac{3}{4}; - \frac{3}{10})$

D. $(x; y) = (0; 1); (\frac{10}{3}; \frac{4}{3}); (- \frac{13}{4}; - \frac{13}{10})$

Hướng dẫn giải:

Chọn B.

Ta có các số $5 x - y, 2 x + 3 y, x + 2 y$ lập thành CSC nên suy ra $2 (2 x + 3 y) = 5 x - y + x + 2 y$ hay $2 x = 5 y$ (1)

Các số ${(y + 1)}^{2}, x y + 1, {(x - 1)}^{2}$ lập thành CSN suy ra

${(x y + 1)}^{2} = {(y + 1)}^{2} {(x - 1)}^{2} \Leftrightarrow (4 + 2 y - 2 x) (4 x y + 2 x - 2 y) = 0$ (2)

Thay (1) vào (2) ta được : $(4 + 2 y - 5 y) (10 y^{2} + 5 y - 2 y) = 0$

$\Leftrightarrow y (4 - 3 y) (10 y + 3) = 0 \Leftrightarrow y = 0, y = \frac{4}{3}, y = - \frac{3}{10}$ .

Vậy $(x; y) = (0; 0); (\frac{10}{3}; \frac{4}{3}); (- \frac{3}{4}; - \frac{3}{10})$ .

Câu 24: Cho cấp số cộng (u_n) có u₁ = 1 và d = – 3.

a) Xác định số hạng tổng quát của cấp số cộng

b) Tìm số hạng thứ 2021 của cấp số cộng

c) Số – 488 là số hạng thứ bao nhiêu của cấp số cộng.

Lời giải

a) Số hạng tổng quát:

u_n = u₁ + (n – 1)d = 1 + (n – 1).(– 3) = – 3n + 4.

b) Số hạng thứ 2021 của cấp số cộng:

u₂₀₂₁ = – 3.2021 + 4 = – 6059.

c) Gọi số hạng thứ k là số – 488, ta có: u_k = – 3k + 4 = – 488. Suy ra k = 164.

Vậy số – 488 là số hạng thứ 164.

Câu 25: Cho cấp số cộng (u_n) thỏa mãn 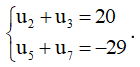Công thức tìm số hạng tổng quát của cấp số cộng hay nhất | Toán lớp 11

a) Tìm u₁; d?

b) Xác định số hạng tổng quát của cấp số cộng.

c) Số –1372,5 là số hạng thứ bao nhiêu của cấp số cộng.

Lời giải

a) Ta có:

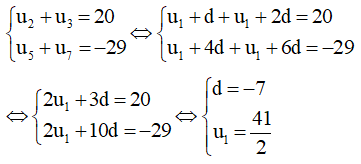
Công thức tìm số hạng tổng quát của cấp số cộng hay nhất | Toán lớp 11

Vậy 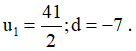Công thức tìm số hạng tổng quát của cấp số cộng hay nhất | Toán lớp 11

b) Số hạng tổng quát:

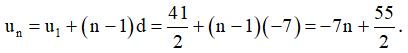
Công thức tìm số hạng tổng quát của cấp số cộng hay nhất | Toán lớp 11

c) Gọi số hạng thứ k là số – 1372,5, ta có: 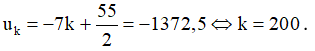Công thức tìm số hạng tổng quát của cấp số cộng hay nhất | Toán lớp 11

Vậy số – 1372,5 là số hạng thứ 200.

Tài liệu có 6 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm