Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Số nguyên là gì? Tập hợp Z, tính chất và các dạng bài tập, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Số nguyên, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Số nguyên là gì? Tập hợp Z, tính chất và các dạng bài tập 

A. Lý thuyết Số nguyên, Tập hợp Z

1. Số nguyên

Số nguyên dương: $1;2;3;4;...$ (Số tự nhiên khác 0)

Số nguyên âm: $-1;-2;-3;-4;...$(Ta thêm dấu “-” vào đằng trước các số nguyên dương)

- Tập hợp: $\left\{...;-3;-2;-1;0;1;2;3;...\right\}$ gồm các số nguyên âm, số $0$ và các số nguyên dương là tập hợp các số nguyên.

Kí hiệu là $\mathbb{Z}=\left\{...;-3;-2;-1;0;1;2;3;...\right\}$

* Số 0 có phải số nguyên không

Dựa vào định nghĩa số nguyên ta được: Số 0 là số nguyên

Chú ý:

- Số $0$ không phải là số nguyên dương cũng không phải số nguyên âm.

- Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn $+5$ (đọc là “dương năm”)

Số nguyên có 4 tính chất cơ bản:

Không có số nguyên nào là lớn nhất và nhỏ nhất.

Số nguyên dương nhỏ nhất là 1. Số nguyên âm nhỏ nhất là -1.

Một tập con hữu hạn bất kỳ của Z luôn có phần tử lớn nhất và phần tử nhỏ nhất.

Không có bất kì số nguyên nào nằm giữa hai số nguyên liên tiếp.

Khi nào người ta dùng số âm?

- Trong đời sống hàng ngày người ta dùng các số mang dấu "-" và dấu "+" để chỉ các đại lượng có thể xét theo hai chiều khác nhau.

Ví dụ:

+) Số $-1$ đọc là “âm một”.

+) Số +2 đọc là “dương hai”

+) Một người thợ lặn lặn xuống độ sâu 10 mét tức là độ cao hiện tại của người thợ lặn là -10m so với mực nước biển.

2. Số đối

Trên trục số, hai số nguyên biểu diễn bởi hai điểm cách đều điểm gốc được gọi là hai số đối nhau. Khi đó, mỗi số được gọi là số đối của số kia.

Chẳng hạn: 1 và -1 là hai số đối của nhau; 1 là số đối của -1, ngược lại -1 là số đối của 1.

Tương tự, 3 và -3; 7 và -7; 1954 và -1954 là những cặp số đối nhau; 3 là số đối của -3; ngược lại -3 là số đối của 3,... 

Đặc biệt: số 0 là số đối của số 0. 

3. Tính chất phép cộng các số nguyên

a. Tính chất giao hoán: $a+b=b+a.$

b. Tính chất kết hợp: $(a+b)+c=a+(b+c).$

Lưu ý: $(a+b)+c$ được gọi là tổng của ba số $a,b,c$ và được viết đơn giản là $a+b+c.$

c. Cộng với số 0:    $a+0=a.$

d. Cộng với số đối:  $a+(-a)=0.$ 

Ví dụ: 

+) Giao hoán: $4+(-3)=(-3)+4$

+) Kết hợp:  $(10+22)+(-10)=[10+(-10)]+22$

+) Cộng với số 0: $5+0=0+5=5$

+) Cộng với số đối: $31+(-31)=0$

+) Tính chất phân phối: $4(12+24)=4.12+4.24$

4. Thứ tự trên tập hợp số nguyên

a) Trục số

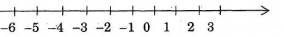
- Chiều dương hướng từ trái sang phải (thường được đánh dấu bằng mũi tên), chiều ngược lại là chiều âm.

- Điểm gốc của trục số là điểm $0$.

- Điểm biểu diễn số nguyên $a$ gọi là điểm $a$.

- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm $0$ với điểm $1$.

+) Cho số nguyên $a$ và $b$. Trên trục số, nếu điểm $a$ nằm bên trái điểm $b$ thì số $a$ nhỏ hơn số $b$, kí hiệu $a<b$

Ví dụ:

Số 2 trên trục số được gọi là điểm 2.

Số $-9$ trên trục số được gọi là điểm $-9$

Ví dụ: Cho trục số như hình vẽ.

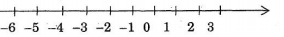
Ta thấy điểm biểu diễ số $-5$ nằm bên trái điểm biểu diễn số $-3$ nên $-5<-3.$

Ngoài ra, ta cũng có thể biểu diễn số nguyên trên trục số thẳng đứng.

5. So sánh hai số nguyên

- Mọi số nguyên âm đều nhỏ hơn 0.

- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.

- Mọi số nguyên dương đều lớn hơn 0.

- Nếu $a,b$ là hai số nguyên dương và $a>b$ thì $-a<-b$ (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)

- Nếu $a,b$ là hai số nguyên dương và $a<b$ thì $-a>-b$

- Kí hiệu $a\le b$ có nghĩa là “$a<b$ hoặc $a=b$”

- Kí hiệu $a\ge b$ có nghĩa là “$a>b$ hoặc $a=b$”

Chú ý: 

+) Để so sánh 2 số nguyên âm, ta làm 2 bước sau:

Bước 1: Bỏ dấu "-" trước cả 2 số âm 

Bước 2: Trong 2 số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu( trước khi bỏ dấu "-" lớn hơn

Ví dụ:

5 là số nguyên dương và $-25$ là số nguyên âm nên $5>-25$

Vì $15>3$ nên $-15<-3$

B. Các dạng bài tập số nguyên

1. Dùng số nguyên để diễn tả các tình huống thực tiễn

- Cách dùng để diễn tả nhiệt độ

+ Số nguyên âm được dùng để chỉ nhiệt độ dưới $0^{o}C$.

+ Số nguyên dương được dùng để chỉ nhiệt độ trên $0^{o}C$.

- Cách dùng để chỉ độ cao so với mực nước biển

+ Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.

+ Số nguyên dương được dùng để chỉ độ cao trên mực nước biển.

- Cách dùng để chỉ số tiền lãi (lỗ), số tiền nợ

+ Số nguyên âm được dùng để chỉ số tiền nợ, cũng như chỉ số tiền lỗ trong kinh doanh

+ Số nguyên dương được dùng để chỉ số tiền lãi trong kinh doanh.

- Cách dùng để chỉ thời gian trước và sau công nguyên

+ Số nguyên âm được dùng để chỉ thời gian trước công nguyên.

+ Số nguyên dương được dùng để chỉ thời gian sau công nguyên.

2. Tập hợp số nguyên, phân biệt các số thuộc tập hợp số tự nhiên và số nguyên

Phương pháp: Sử dụng định nghĩa các tập hợp số sau đây:

- Tập hợp số tự nhiên: $\mathbb{N}=\left\{0;1;2;3;....\right\}$

- Tập hợp số tự nhiên khác 0: ${\mathbb{N}}^{\ast }=\left\{1;2;3;....\right\}$

- Tập hợp số nguyên: $\mathbb{Z}=\left\{...;-2;-1;0;1;2;...\right\}$

+ Các số nguyên âm: $-1;-2;-3;-4;...$

+ Các số nguyên dương: $1;2;3;4;...$

Chú ý: Số 0 không là số nguyên âm cũng không là số nguyên dương.

3. Biểu diễn các số nguyên trên trục số

- Trên trục số nằm ngang:

+ Các điểm biểu diễn số nguyên âm nằm ở bên trái gốc 0

+ Các điểm biểu diễn số nguyên dương nằm ở bên phải gốc 0.

- Trên trục số thẳng đứng:

+ Các điểm biểu diễn số nguyên âm nằm ở bên dưới gốc 0

+ Các điểm biểu diễn số nguyên dương nằm ở bên trên gốc 0.

4. Bài toán so sánh hai số nguyên

a) So sánh hai số nguyên trái dấu

Số nguyên âm luôn nhỏ hơn số nguyên dương.

b) So sánh hai số nguyên cùng dấu

Để so sánh hai số nguyên âm, ta làm như sau:

Bước 1: Bỏ dấu “-” trước cả hai số âm.

Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (tương ứng) sẽ lớn hơn.

5. Tìm số nguyên thuộc một khoảng cho trước

Dựa vào qui tắc so sánh các số nguyên để chọn ra các số nguyên thích hợp.

Ví dụ:

Tìm số nguyên $x$ thỏa mãn: $-2<x\le 1$

Ta thấy các số nguyên lớn hơn $-2$ và nhỏ hơn hoặc bằng $1$ thỏa mãn đề bài nên:

$x\in \left\{-1;0;1\right\}$.

C. Bài tập Số nguyên

1. Bài tập tự luận

Bài 1. Dùng số âm để diễn tả các thông tin sau:

a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến 60⁰C dưới 0⁰C.

b) Do dịch bệnh, một công ty trong một tháng đã bị lỗ 2 triệu đồng.

Lời giải

a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến - 60⁰C.

b) Do dịch bệnh, một công ty một tháng có – 2 triệu đồng.

Bài 2. Tính một cách hợp lí:

a) 15.(-236) + 15.235;

b) 237.(-28) + 28.137;

c) 38.(27 – 44) – 27.(38 – 44).

Lời giải

a) 15.(-236) + 15.235

= 15.[(-236) + 235]

= 15.(-1)

= -15.

b) 237.(-28) + 28.137

= (-237).28 + 28.137

= 28.[(-237) + 137]

= 28.(-100)

= -2 800.

c) 38.(27 – 44) – 27.(38 – 44).

= 38.27 – 38.44 – 27.38 + 27.44

= 38.27 – 27.38 – 38.44 + 27.44

= 0 + 44.(-38 + 27)

= 0 + 44.(-11)

= - 484.

Bài 3. Có hay không hai số nguyên a và b mà hiệu a – b :

a) Lớn hơn cả a và b?

b) Lớn hơn a nhưng nhỏ hơn b?

Lời giải

a) Có trường hợp a – b > a hoặc a – b > b 

Ví dụ: a = 10 và b = - 15

Ta có a – b = 10 – (-15) = 10 + 15 = 25.

Khi đó 25 > 15 và 25 > - 15.

b) Có trường hợp hiệu a – b lớn hơn a nhưng nhỏ hơn b:

Ví dụ: a = - 3, b = -1, a – b = -3 – (-1) = -2 .

Vì -3 < -2 < -1 hay a < a – b < b.

ta còn gọi a là một bội của b và b là một ước của a.

Nhận xét: 

Nếu a là một bội của b thì –a cũng là một bội của b.

Nếu b là một ước của a thì – b cũng là một ước của a.

2. Bài tập vận dụng

Bài 1. Liệt kê các phần tử của mỗi tập hợp sau:

a) B = {x ∈ Z | -3 ≤ x ≤ 4} ;

b) B = {x ∈ Z | -2 ≤ x ≤ 0}.

Lời giải

a) A = {-3; -2; -1; 0; 1; 2; 3}.

b) B = {-2; -1; 0}.

Bài 2. So sánh hai số:

a) -49 và -38;   

b) -1379 và – 2379.

Lời giải

a) Vì 49 > 38 nên -49 < -38.

b) Vì 2379 > 1379 nên -2379 < -1379.

Bài 3. Hãy sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau:

a) Mùa đông ở Siberia (Nga) dài và khắc nghiệt, với nhiệt độ trung bình tháng 1 là 25^oC  dưới 0^oC  .

b) Cá voi xanh có thể lặn sâu 2500m có với mực nước biển.

Lời giải

a) Nhiệt độ trung bình tháng 1 của Siberia (Nga) được biểu diễn là: -25^oC .

b) Độ sâu mà Cá voi xanh có thể lặn được biểu diễn là: – 2500 m.