Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Ước chung lớn nhất là gì? Cách tìm ước chung lớn nhất, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Ước chung lớn nhất, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Ước chung lớn nhất là gì? Cách tìm ước chung lớn nhất

A. Lý thuyết Ước chung lớn nhất

1. Ước là gì?

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

Ví dụ: Ta có 12 ⋮ 6.

Khi đó, 12 là bội của 6, còn 6 là ước của 12.

2. Ước chung và ước chung lớn nhất là gì?

Ước chung của hai hay nhiều số là ước của tất cả các số đó.

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Ta kí hiệu:

ƯC(a, b) là tập hợp các ước chung của a và b.

ƯCLN(a, b) là ước chung lớn nhất của a và b.

3. Công thức tìm ước chung lớn nhất

a) Tìm ước chung lớn nhất của hai hay nhiều số lớn hơn 1:

- Bước 1: Phân tích mỗi số ra thừa số nguyên tố;

- Bước 2: Chọn ra các thừa số nguyên tố chung;

- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

* Chú ý:

- Nếu $a⋮b$ thì ƯCLN (a, b) = b.

- ƯCLN (a, 1) = 1; ƯCLN (a, b, 1) = 1.

b) Tìm ước chung từ ước chung lớn nhất:

- Bước 1: Tìm ƯCLN của các số đó.

- Bước 2: Tìm các ước của ƯCLN đó.

4. Ứng dụng ước chung và ước chung lớn nhất để giải các bài toán thực tế

Sử dụng kiến thức về ước chung và ước chung lớn nhất đã được học để giải các bài toán thực tế.

- Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:

Bước 1:  Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

+ Trường hợp đặc biệt:

Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.

Số 1 chỉ có một ước là 1. Do đó với mọi số tự nhiên a và b, ta có:

ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1

- Các bước tìm ước chung

Để tìm ước chung của các số, ta làm như sau:

Bước 1: Tìm ƯCLN của các số đó.

Bước 2: Tìm các ước của các ƯCLN đó.

Ví dụ 1. Lan có một tấm bìa hình chữ nhật, kích thước 75cm và 105cm, Lan muốn cắt tấm bìa thành các mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết không còn thừa mảnh nào. Tính độ dài lớn nhất cạnh hình vuông?

Hướng dẫn giải:

Gọi độ dài cạnh các mảnh của hình vuông là a (cm) (a $\in$$\mathbb{N}$, a < 75)

Theo bài ra ta có: 75 $⋮$ a, 105$⋮$ a và a là lớn nhất

Nên a = ƯCLN(75, 105)

Ta phân tích 75 và 105 ra thừa số nguyên tố:

75 = 3.5²

105 = 3.5.7

Ta thấy 3 và 5 là các thừa số nguyên tố chung của 75 và 105. Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1 nên:

ƯCLN(75, 105) = 3.5 = 15

Vậy độ dài cạnh lớn nhất của hình vuông là 15.

Ví dụ 2. Có 30 miếng dứa và 40 miếng dưa hấu. Hỏi có bao nhiêu cách chia chúng vào các cái đĩa sao cho số miếng mỗi loại trong các đĩa là như nhau?

Hướng dẫn giải:

Gọi gọi số đĩa được chia là a (đĩa) (a $\in$$\mathbb{N}$, a < 30)

Theo bài ra ta có: 30 $⋮$ a, 40 $⋮$ a. Khi đó a $\in$ ƯC(30, 40)

Ta phân tích 30 và 40 ra thừa số nguyên tổ:

30 = 2.3.5

40 = 2³.5

Ta thấy 2; 5 là thừa số nguyên tố chung của 30; 40. Số mũ nhỏ nhất của 2 là 1, số mũ của 5 là 1 nên:

ƯCLN(30, 40) = 2.5 = 10

Các ước của 10 là: 1; 2; 5; 10.

Vậy có 4 cách chia

Ví dụ 3.  Đội văn nghệ của một trường có 48 nam và 72 nữ về 1 huyện để biểu diễn, đội đã chia các tổ gồm cả nam và nữ, biết số nam, số nữ được chia đều vào các tổ vậy có thể chia được nhiều nhất bao nhiêu tổ?

Hướng dẫn giải:

Gọi số tổ có thể chia được nhiều nhất là a (tổ) (a $\in$$\mathbb{N}$, a < 48)

Theo bài ra ta có: 48 $⋮$ a, 72 $⋮$ a và a là lớn nhất

Nên a = ƯCLN(48, 72)

Ta phân tích 48 và 72 ra thừa số nguyên tố:

48 = 2⁴.3

72 = 2³.3²

Ta thấy 2 và 3 là các thừa số nguyên tố chung của 48 và 72. Số mũ nhỏ nhất của 2 là 3, số mũ nhỏ nhất của 3 là 1 nên:

ƯCLN(48, 72) = 2³.3 = 24

Vậy có thể chia được nhiều nhất 24 tổ.

B. Các dạng bài tập Ước chung lớn nhất

Bài tập trắc nghiệm

Dạng 1. Ước chung và ước chung lớn nhất

Câu 1. Sau khi phân tích 45, 150 ra các thừa số nguyên tố. Tất cả các thừa số chung của hai số này là:

A. 2 và 3

B. 2 và 5

C. 3 và 5

D. 5

Trả lời:

45 = 32.5  có hai thừa số nguyên tố là 3 và 5

150 = 2.3.52 có 3 thừa số nguyên tố là 2, 3 và 5.

Các thừa số chung là 3 và 5.

Đáp án: C

Câu 2. Phân số $\frac{16}{10}$ được rút gọn về phân số tối giản là:

A. $\frac{16}{10}$

B. $\frac{8}{5}$

C. 2

D. $\frac{4}{5}$

Trả lời:

ƯC(15; 10) = 2. Ta chia cả tử và mẫu của $\frac{16}{10}$ cho 2 được:

$\frac{16}{10}=\frac{16:2}{10:2}=\frac{8}{5}$

Đáp án: B

Câu 3. Tìm ước chung của 9 và 15.

A. {1; 3}                      

B. {0; 3}                         

C. {1; 5}                              

D. {1; 3; 9}

Trả lời:

- Ta có:

Ư(9)={1,3,9} và Ư(15)={1,3,5,15}

Vậy ƯC(9,15) = Ư(9)∩ Ư(15) = {1, 3}

Đáp án: A

Câu 4. Số x là ước chung của số a và số b nếu:

A. x∈Ư(a) và x∈B(b)                

B. x⊂Ư(a)và x⊂Ư(b)

C. x∈Ư(a) và x∈Ư(b)   

D. x∉Ư(a) và x∉Ư(b)

Trả lời:

Số x là ước chung của a, b nếu x vừa là ước của a vừa là ước của b.

Đáp án: C

Câu 5. 8 là ước chung của

A. 12 và 32

B. 24 và 56

C. 14 và 48

D. 18 và 24

Trả lời:

24:8=3;

56:8=7

=> 8 là ước chung của 24 và 56.

Đáp án: B

Câu 6. Tìm ƯCLN(18; 60)

A. 6                 

B. 30                           

C. 12                         

D. 18

Trả lời:

Ta có: 

18 = 2.32; 60 = 22.3.5

Nên ƯCLN(18;60) = 2.3 = 6

Đáp án: A

Câu 7. ƯCLN(24, 36) là

A. 36

B. 6

C. 12

D. 24

Trả lời:

Các ước chung của 24 và 36 là 1, 2, 3, 4, 6, 12.

=> ƯC(24, 36) = {1, 2, 3, 4, 6, 12}.

Vì 12 là số lớn nhất trong các ước chung trên nên ƯCLN(24, 36) = 12.

Đáp án: C

Câu 8. Cho ƯCLN(a,b) = 80, ước chung của a và b có thể là:

A. 20

B. 160

C. 30

D. 50

Trả lời:

Ta có 20 là một ước của 80 nên 20 là một ước chung của a và b.

Vậy 20 là số cần tìm.

Đáp án: A

Câu 9. Viết các tập hợp Ư(6); Ư(20); ƯC(6,20).

A. Ư(6) = {1, 2, 3, 6}; Ư(20) = {1, 2, 4, 5, 10, 20}; ƯC(6,20) = {1, 2}

B. Ư(6) = {1, 2, 3, 6}; Ư(20) = {1, 2, 4, 5, 20}; ƯC(6, 20) = {1, 2}

C. Ư(6) = {1, 2, 3}; Ư(20) = {1, 2, 4, 5, 10, 20}; ƯC(6, 20) = {1, 2}

D. Ư(6) = {1, 2, 4, 6}; Ư(20) = {1, 2, 4, 20}; ƯC(6, 20) = {1, 2,4}

Trả lời:

Ta có:

Ư(6) = {1, 2, 3, 6} và Ư(20) = {1, 2, 4, 5, 10, 20}

Vậy ƯC(6, 20) = {1, 2}

Đáp án: A

Dạng 2. Các dạng toán về ước chung và ước chung lớn nhất

Câu 1. Hoa có 48 viên bi đỏ, 30 viên bi xanh và 60 viên bi vàng. Hoa muốn chia đều số bi vào các túi, sao cho mỗi túi có đủ 3 loại bi. Hỏi Hoa có thể chia vào nhiều nhất bao nhiêu túi mà mỗi túi có số bi mỗi màu bằng nhau.

A. 6                    

B. 8                  

C. 4            

D. 12

Trả lời:

Ta có: 
Gọi số túi mà Hoa chia được là x  (túi) 
Vì số bi mỗi màu ở mỗi túi cũng bằng nhau nên 48⋮x ; 30⋮x và 60⋮x
⇒x∈ ƯC(48; 30; 60)
Vì x là lớn nhất nên x = ƯCLN(48; 30; 60)
Ta có: 48=24.3

48=2⁴.3; 30=2.3.5; 60=2².3.5
⇒x = ƯCLN(48; 30; 60) = 2.3 = 6
Vậy Hoa chia được nhiều nhất là 6 túi mà mỗi túi có số bi mỗi màu bằng nhau.

Đáp án: A

Câu 2. ƯCLN của a và b là:

A. Bằng b nếu a chia hết cho b              

B. Bằng a nếu a chia hết cho b

C. Là ước chung nhỏ nhất của a và b

D. Là hiệu của 2 số a và b

Trả lời:

Nếu a chia hết cho b thì b là ước của a.

Mà b cũng là ước của b nên b∈ƯC(a;b)

Hơn nữa bb là ước lớn nhất của bb nên ƯCLN(a,b) = b

Đáp án: A

Câu 3. Tìm ƯCLN của 15, 45 và 225.

A. 18                    

B. 3                  

C. 15            

D. 5

Trả lời:

Ta có: 15=3.5; 45=3².5; 225=5².3²

Nên ƯCLN(15;45;225) = 3.5 = 15

Đáp án: C

Câu 4. Giao của tập của hai tập hợp  A={toán, văn, thể dục, ca nhạc} và B={mỹ thuật, toán, văn, giáo dục công dân}.

A. C={toán, văn, thể dục}

B. C={toán, văn}

C. C={toán, văn, thể dục, ca nhạc}

D. C={toán, thể dục, giáo dục công dân}

Trả lời:

Gọi C=A∩B

Vậy C={toán, văn}

Đáp án: B

Câu 5. Tìm các ước chung của 18;30;42.

A. {2; 3; 6}                               

B. {1; 2; 3; 6}                                 

C. {1; 2; 3}      

D. {1; 2; 3; 6; 9}

Trả lời:

+) Ư(18) = {1; 2; 3; 6; 9; 18}

+) Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}

+) Ư(42) = {1; 2; 3; 6; 7; 12; 14; 21; 42}

Nên ƯC(18; 30; 42) = {1; 2; 3; 6}

Đáp án: B

Câu 6. Tìm x lớn nhất biết x + 220 và x + 180 đều chia hết cho x.

A. 15                    

B. 10                    

C. 20                    

D. 18                    

Trả lời:

Vì x + 220 và x + 180 đều là bội của x nên (x+220)⁝x và (x+180)⁝x
Vì x⁝x ⇒220⁝x và 180⁝x

⇒ x ƯC(220; 180)
Vì x lớn nhất ⇒ xƯCLN(220; 180)

220 = 22.5.11 ; 180 = 22.32.5
⇒ x = ƯCLN(220;180) = 22.5 = 20

Đáp án: C

Câu 7. Một căn phòng hình chữ nhật dài 680cm, rộng  480cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu? 

A. 5cm                    

B. 10cm                  

C. 20cm            

D. 40cm

Trả lời:

Ta có: 
Gọi chiều dài viên gạch là x.
Để lát kín căn phòng mà không có có viên gạch nào bị cắt xén thì xx phải là ước của chiều dài và chiều rộng căn phòng 
Hay 680⋮x và 480⋮x

⇒x∈ ƯC(680;480)
Để x là lớn nhất ⇒ x = ƯCLN(680;480)
Ta có: 680 = 23.5.17; 480 = 25.3.5
⇒ x = ƯCLN(680;480) = 23.5 = 40
Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là 40 cm.

Đáp án: D

Câu 8. Một khu đất hình chữ nhật có chiều dài 60m, rộng 24m. Người ta chia thành những thửa đất hình vuông bằng nhau, để mỗi thửa đất đó có diện tích lớn nhất thì độ dài cạnh mỗi thửa đất đó là bao nhiêu? 

A. 8m                    

B. 24m                  

C. 12m            

D. 6m

Trả lời:

Gọi cạnh mỗi thửa đất hình vuông chia được là x(m)
Để diện tích các thửa đất đó là lớn nhất thì x phải lớn nhất 
Vì các thửa đất đó được chia ra từ đám đất hình chữ nhật ban đầu có chiều dài 60m và 24m 
Nên x phải là ước của 60 và 24 
Hay x∈ƯC(60; 24)
Vì x là lớn nhất nên x=  ƯCLN(60;24)  
Ta có: 

60=2².3.5; 24=2³.3

⇒x = ƯCLN(60; 24) = 2².3 = 12.
Vậy mỗi thửa đất hình vuông đó có độ dài cạnh lớn nhất là 12m.12m.

Đáp án: C

Câu 9. Cho a = 3².5.7; b = 2⁴.3.7. Tìm ƯCLN của a và b.

A. ƯCLN(a,b)=3.7

B. ƯCLN(a,b) =  3².7²                  

C. ƯCLN(a,b) = 2⁴.5            

D. ƯCLN(a,b) = 24⁴.3².5.7

Trả lời:

Ta có a = 3².5.7; b = 2⁴.3.7 nên ƯCLN(a,b) = 3.7

Đáp án: A

Câu 10. Chọn khẳng định đúng:

A. Mọi số tự nhiên đều có ước chung với nhau.               

B. Mọi số tự nhiên đều có ước là 0                   

C. Số nguyên tố chỉ có đúng 1 ước là chính nó.              

D. Hai số nguyên tố khác nhau thì không có ước chung

Trả lời:

A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là 1

B. Đáp án này sai, vì 0 không là ước của 1 số nào cả.

C. Đáp án này sai, vì số nguyên tố có 2 ước là 1 và chính nó.

D. Đáp án này sai, vì 2 số nguyên tố có ước chung là 1.

Đáp án: A

Bài tập vận dụng

Bài 1. Cho hai số a = 132, b = 36.

a) Phân tích a và b ra thừa số nguyên tố.

b) Tìm ƯCLN(a, b) và ƯC(a, b).

Lời giải

a) 132 = 2².3.11;            36 = 2².3².

b) ƯCLN(132, 36) = 2².3 = 12.

ƯC(132, 36) = {1; 2; 3; 4; 6; 12}.

Bài 2. Các phân số sau đã tối giản chưa? Nếu chưa hãy rút gọn phân số đến phân số tối giản.

Lời giải

Tất cả các phân số đã cho đều chưa tối giản.

a) Vì 15050 nên ƯCLN(150, 50) = 50.

Để rút gọn phân số ta chia cả tử và mẫu cho 50, ta được:

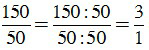= 3

b) Ta có: 90 = 2.3².5, 27 = 3³.

ƯCLN(90,27) =3² = 9.

Để rút gọn phân số ta chia cả tử và mẫu cho 9, ta được:

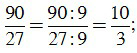
c) Ta có: 34 = 2.17, 255 = 3.5.17.

ƯCLN(34, 255) = 17.

Để rút gọn phân số ta chia cả tử và mẫu cho 17, ta được:

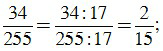
d) Ta có: 88 = 2³.11, 121 = 11²

ƯCLN(88, 121) = 11.

Để rút gọn phân số ta chia cả tử và mẫu cho 11, ta được:

.

Bài tập tự luyện

Câu 1. Một đội y tế có 24 bác sĩ và 108 y tá, có thể chia đội y tế đó thành nhiều nhất mấy tổ để các bác sĩ, y tá được chia đều vào các tổ?

A. 6;

B. 12;

C. 8;

D. 3.

Câu 2. Trong một buổi liên hoan ban tổ chức đã mua 96 cái kẹo và 36 cái bánh và được chia đều ra các đĩa gồm cả kẹo và bánh, có thể chia được nhiều nhất bao nhiêu đĩa?

A. 6;

B. 12;

C. 8;

D. 3.

Câu 3. Lớp 6A có 54 học sinh, 6B có 42 và 6C có 48 học sinh, trong ngày khai giảng ba lớp cùng xếp thành 1 số hàng dọc như nhau, mà không có người lẻ hàng. Tính số hàng dọc nhiều nhất có thể xếp được?

A. 2;

B. 3;

C. 6;

D. 8.

Câu 4. Có 48 bút chì, 64 quyển vở, cô giáo muốn chia số bút và số vở thành 1 số phần thưởng như nhau, có thể chia được nhiều nhất bao nhiêu phần thưởng, số bút và số vở ở mỗi phần thưởng?

A. 16 phần thưởng, 3 cái bút, 4 quyển vở;

B. 8 phần thưởng, 6 cái bút, 8 quyển vở;

C. 4 phần thưởng, 12 cái bút, 16 quyển vở;

D. 2 phần thưởng, 24 cái bút, 32 quyển vở.

Câu 5. Bạn Lan có 48 viên bi đỏ, 30 viên bi xanh, 66 bi vàng, Lan muốn chia đều số bi vào các túi sao cho mỗi túi đều có 3 loại bi. Hỏi Lan có thể chia được nhiều nhất bao nhiêu túi, mỗi túi có bao nhiêu viên bi đỏ?

A. 3 túi, 16 bi đỏ;

B. 6 túi, 8 bi đỏ;

C. 2 túi, 24 bi đỏ;

D. 8 túi, 6 bi đỏ.

Câu 6. Một bác thợ mộc muốn làm kệ để đồ từ hai tấm gỗ dài 15 dm và 30 dm. Bác muốn cắt hai tấm gỗ này thành các thanh gỗ có cùng độ dài mà không để thừa mẩu gỗ nào. Độ dài lớn nhất có thể của mỗi thanh gỗ được cắt là?

A. 3;

B. 5;

C. 15;

D. 10.

Câu 7. Một mảnh đất hình chữ nhật có chiều dài 120m, chiều rộng 36m, người ta muốn trồng cây xung quanh vườn sao cho mỗi góc vườn có 1 cây và khoảng cách giữa hai cây liên tiếp bằng nhau. Hỏi số cây phải trồng ít nhất là bao nhiêu cây?

A. 26;

B. 52;

C. 78;

D. 104.

Câu 8. Một lớp có 28 học sinh nam và 24 học sinh nữ. Khi phân tổ, GVCN muốn phân chia sao cho số HS nam và số HS nữ mỗi tổ đều bằng nhau. Hỏi có bao nhiêu cách chia tổ? (tổ khi chia phải nhiều hơn 1)

A. 1;

B. 2;

C. 3;

D. 4.

Câu 9. Hai lớp 6A và 6B tham gia phong trào tết trồng cây, mỗi em trồng 1 số cây như  nhau, kết quả lớp 6A trồng được 132 cây và 6B được 135 cây. Hỏi mỗi lớp có bao nhiêu học sinh? (mỗi em trồng nhiều hơn 1 cây)

A. 6A: 43 học sinh; 6B: 45 học sinh;

B. 6A: 44 học sinh; 6B: 45 học sinh;

C. 6A: 42 học sinh; 6B: 45 học sinh;

D. 6A: 44 học sinh; 6B: 46 học sinh.

Câu 10. Có 48 học sinh nam và 60 học sinh nữ được chia đều thành các nhóm để biểu diễn văn nghệ. Hỏi có thể chia nhiều nhất thành bao nhiêu nhóm? Khi đó mỗi nhóm có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?

A. Chia thành 4 nhóm; mỗi nhóm có 12 học sinh nam, 15 học sinh nữ;

B. Chia thành 2 nhóm; mỗi nhóm có 24 học sinh nam, 30 học sinh nữ;

C. Chia thành 3 nhóm; mỗi nhóm có 16 học sinh nam, 20 học sinh nữ;

D. Chia thành 12 nhóm; mỗi nhóm có 4 học sinh nam, 5 học sinh nữ.