Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Tính chất ba đường trung tuyến của tam giác Toán lớp 7, tài liệu bao gồm 14 trang, tuyển chọn bài tập Tính chất ba đường trung tuyến của tam giác đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC
A. Lý thuyết Tính chất ba đường trung tuyến của tam giác
1. Đường trung tuyến của tam giác
Đường trung tuyến của tam giác là đoạn thẳng có một đầu là đỉnh của tam giác đầu kia là trung điểm của cạnh đối diện với đỉnh đó.
Mỗi tam giác có ba đường trung tuyến.
Ví dụ: Tam giác có là trung điểm cạnh thì là một đường trung tuyến của tam giác
Như vậy, nếu lần lượt là trung điểm của ba cạnh thì là ba đường trung tuyến của tam giác
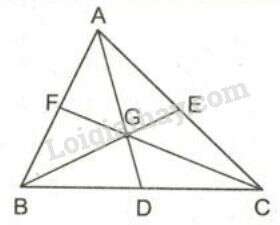
2. Tính chất ba đường trung tuyến của tam giác
Định lý: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
Giao điểm của ba đường trung tuyến gọi là trọng tâm.
GT : có lần lượt là trung điểm của ba cạnh và là trọng tâm
KL :
3. Các dạng toán thường gặp
Dạng 1: Tìm các tỉ lệ giữa các cạnh, tính độ dài đoạn thẳng
Phương pháp:
Chú ý đến vị trí trọng tâm của tam giác.
Với G là trọng tâm của và là ba đường trung tuyến ta có
Dạng 2: Đường trung tuyến với các tam giác đặc biệt (tam giác cân, tam giác đều, tam giác vuông)
Phương pháp:
Chú ý rằng trong tam giác cân ( hoặc tam giác đều) đường trung tuyến ứng với cạnh đáy chia tam giác thành hai tam giác bằng nhau.
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
B. Ví dụ minh họa
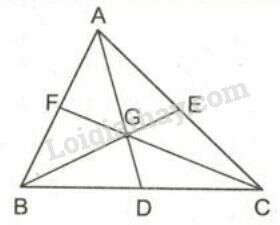
Ví dụ 1: Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G. Trên tia GB và GC lấy các điểm F và E sao cho G là trung điểm của FM đồng thời là trung điểm của EN. Chứng minh rằng ba đường thẳng AG, BE và CF đồng quy.
Giải (h.18.2)
* Tìm cách giải.
Để chứng minh ba đường thẳng AG, BE và CF đồng quy ta có thể chứng minh chúng là ba đường trung tuyến của tam giác GBC.
* Trình bày lời giải.
Gọi D là giao điểm của AG và BC. Vì G là trọng tâm của nên AD là đường trung tuyến, suy ra
Ta có
Do đó
Xét có GD, BE, CF là ba đường trung tuyến nên chúng đồng quy suy ra ba đường thẳng AD, BE, CF đồng quy.
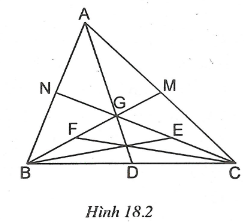
Ví dụ 2: Cho tam giác ABC. Trên nửa mặt phẳng bờ AB không chứa C vẽ tia . Lấy điểm và điểm E thuộc tia đối của tia CA sao cho BD = CE. Chứng minh rằng và có cùng một trọng tâm.
Giải (h.18.3)
* Tìm cách giải
Tam giác ABC và ADE có chung đỉnh A nên muốn chứng minh chúng có cùng một trọng tâm, chỉ cần chứng minh chúng có chung một đường trung tuyến xuất phát từ đỉnh A.
* Trình bày lời giải.
Vì nên (so le trong).
Gọi M là trung điểm của BC.
Ta có (c.g.c).
Suy ra và
Ta có (kề bù).
Do đó D, M, E thẳng hàng. (2)
Từ (1) và (2) suy ra M là trung điểm của DE.
và chung đỉnh A, chung đường trung tuyến AM nên trọng tâm G của hai tam giác này trùng nhau.
* Nhận xét: Để chứng minh hai tam giác có cùng trọng tâm ta có thể chứng minh chúng có chung một đỉnh và chung đường trung tuyến đi qua đỉnh ấy.
Ví dụ 3: Cho ΔABC, trên cạnh BC lấy điểm T sao cho TB = 2/3 BC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Đường thẳng DT cắt AB tại E. Chứng minh EA = EB
Lời giải:
Trong ΔABD có: BC là trung tuyến vì CD = CA
Và TB = 2/3 BC, do đó T là trọng tâm của ΔABD
Suy ra DT là đường thẳng chứa trung tuyến xuất phát từ D
Nên phải qua trung điểm E của cạnh AB.
Vậy EA = EB
C. Bài tập vận dụng
Bài 1: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy hai điểm A, B sao cho A nằm giữa O và B, AB = 2OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của LM. Nối B với L, B với M và gọi P là trung điểm của đoạn MB, Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.
Lời giải:
Ta có O là trung điểm của đoạn LM
Suy ra BO là đường trung tuyến của ΔBLM (1)
Mặt khác BO = BA + AO vì A nằm giữa O và B hay OB = 2OA + OA = 3OA
Suy ra AO = (1/3)OB hay BA = (2/3)BO (2)
Từ (1) (2) suy ra A là trọng tâm của ΔBLM (tính chất trọng tâm)
Mà LP và MQ là các đường trung tuyến của ΔBLM vì P là trung điểm MB và Q là trung điểm của đoạn LB
Suy ra các đoạn thẳng LP và MQ đi qua A (theo tính chất 3 đường trung tuyến)
Bài 2: Cho ΔABC, BC = a, CA = b, AB = c. Kẻ trung tuyến AM. Đặt AM = ma. Chứng minh rằng
Lời giải:
Bài 3: Cho tam giác ABC, đường trung tuyến AD. Trên tia đối của tia DA lấy điểm K sao cho Qua B vẽ một đường thẳng song song với CK cắt AC tại M. Chứng minh rằng M là trung điểm của AC.
Bài 4: Cho tam giác ABC cân tại A có đường phân giác AD.
a) Chứng minh: Điểm D là gì?
b) Chứng minh đường phân giác AD và 2 đường trung tuyến BE, CF của tam giác ABC đồng qui tại một điểm.
Bài 5: Cho tam giác ABC có hai đường trung tuyến BE và CF cắt nhau ở G. D là trung điểm BC. Đường AD là đường gì và điểm G là điểm gì trong tam giác ABC? Chứng minh: A, G, D thẳng hàng.
Bài 6: Cho tam giác ABC có hai đường trung tuyến BE và CF cắt nhau ở G. AG kéo dài cắt BC tại M. Chứng minh:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
