Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Cách tìm Điều kiện để 2 vecto cùng phương hay, chọn lọc, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Cách tìm Điều kiện để 2 vecto cùng phương hay, chọn lọc

1. Định nghĩa vecto

Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểm đầu, điểm B làm điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.

* Định nghĩa

Vectơ là một đoạn thẳng có hướng.

Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow{AB}$ và đọc là "vectơ AB". Để vẽ vectơ $\overrightarrow{AB}$ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B.

Vectơ còn được kí hiệu là $\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},$ ...khi không cần chỉ rõ điểm đầu và điểm cuối của nó.

2. Phương pháp giải bài tập

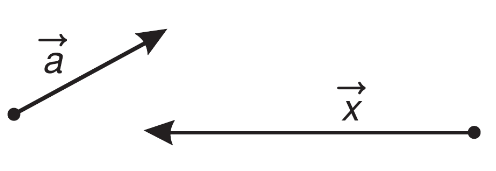
+ Hai vecto a→ và b→ cùng phương nếu giá của chúng song song hoặc trùng nhau.

+ Để chứng minh hai vecto cùng phương ta có thể làm theo hai cách sau:

    - Chứng minh giá của chúng song song hoặc trùng nhau.

    - Chứng minh tồn tại số thực k ≠ 0: $\stackrel{\rightharpoonup }{a}$ = k.b→

3. Bài tập minh họa

Ví dụ 1: Cho u→ = 2a→ + b→ và v→ = -6$\stackrel{\rightharpoonup }{a}$ - 3b→. Chọn mệnh đề đúng nhất?

A. Hai vecto u→ và v→ là cùng phương

B. Hai vecto u→ và v→ là cùng phương và cùng hướng

C. Hai vecto u→ và v→ là cùng phương và ngược hướng

D. Hai vecto u→ và v→ là không cùng phương

Hướng dẫn giải

Ta có: v→ = -6a→ - 3b→ = -3(2a→ + b→)

⇒ v→ = -3u→

⇒ u→ và v→ là cùng phương và ngược hướng.

Chọn C.

Ví dụ 2: Cho ba vectơ a→, b→, c→ không đồng phẳng. Xét các vectơ x→ = 2a→ - b→, y→ = -4a→ + 2b→, z→ = -3b→ - 2c→. Chọn khẳng định đúng?

A. Hai vectơ y→, z→ cùng phương

B. Hai vectơ x→, y→ cùng phương

C. Hai vectơ x→, z→ cùng phương

D. Ba vectơ x→, y→, z→ đồng phẳng

Hướng dẫn giải

Chọn B

+ Nhận thấy: y→ = -2x→ nên hai vectơ x→, y→ cùng phương.

Ví dụ 3: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Trong các khẳng định sau, khẳng định nào sai?

A. Nếu SA→ + SB→ + 2SC→ + 2SD→ = 6SO→ thì ABCD là hình thang.

B. Nếu ABCD là hình bình hành thì SA→ + SB→ + SC→ + SD→ = 4SO→ .

C. Nếu ABCD là hình thang thì SA→ + SB→ + 2SC→ + 2SD→ = 6SO→.

D. Nếu SA→ + SB→ + SC→ + SD→ = 4SO→ thì ABCD là hình bình hành.

Hướng dẫn giải

Chọn C

A. Đúng vì SA→ + SB→ + 2SC→ + 2SD→ = 6SO→

⇔ OA→ + OB→ + 2OC→ + 2OD→ = O→

Vì O; A; C và O; B; D thẳng hàng nên đặt

B. Đúng.

Ta có:

C. Sai. Vì nếu ABCD là hình thang cân có 2 đáy là AD; BC thì sẽ sai.

D. Đúng. Tương tự đáp án A với k = -1; m = - 1

⇒ O là trung điểm 2 đường chéo.

Ví dụ 4: Cho hai vecto a→ và b→ không cùng phương; u→ = 2a→ - 3b→ và v→ = 3a→ - 9b→. Chọn mệnh đề đúng nhất?

A. Hai vecto u→ và v→ là cùng phương

B. Hai vecto u→ và v→ là cùng phương và cùng hướng

C. Hai vecto u→ và v→ là cùng phương và ngược hướng

D. Hai vecto u→ và v→ là không cùng phương

Hướng dẫn giải

Giả sử tồn tại số thực k sao cho u→ = k.v→

Do hai vecto a→ và b→ không cùng phương nên từ ( 1) suy ra:

⇒ Không có giá trị nào của k thỏa mãn đầu bài.

⇒ Hai vecto u→ và v→ là không cùng phương.

Chọn D

Ví dụ 5: Cho hình hộp ABCD.A’B’C’D’; gọi M và N lần lượt là trung điểm của AD và BC. Chọn mệnh đề đúng?

A. Hai vecto MN→ và DD'→ là cùng phương

B. Hai vecto AM→ và B'C→ là cùng phương

C. Hai vecto AN→ và MC→ là cùng phương

D. Hai vecto DN→ và MA'→ là cùng phương

Hướng dẫn giải

Xét tứ giác AMCN có:

AM = CN = (1/2)BC = (1/2)AD

AM // CN

⇒ Tứ giác AMCN là hình bình hành

⇒ AN // MC nên Hai vecto AN→ và MC→ là cùng phương.

Chọn C

Ví dụ 6: : Cho lăng trụ ABC.A’B’C’; gọi I và J lần lượt là trung điểm của AC và A’C’. Hỏi vecto nào cùng hướng với vecto IJ→?

A. B'B→                        B. C'C→                        C. AA'→                        D. AB'→

Hướng dẫn giải

Ta có tứ giác ACC’A’ là hình bình hành có I và J lần lượt là trung điểm của AC và A’C’

⇒ IJ là đường trung bình của hình bình hành ACC’A’

⇒ IJ // AA’ // CC’

⇒ AA'→ cùng hướng với vecto IJ→

chọn C

4. Bài tập tự luyện

Câu 1: Cho hai vecto a→ và b→ không cùng phương; u→ = a→ - 2b→ và v→ = 3a→ - 5b→. Chọn mệnh đề đúng nhất?

A. Hai vecto u→ và v→ là cùng phương

B. Hai vecto u→ và v→ là cùng phương và cùng hướng

C. Hai vecto u→ và v→ là cùng phương và ngược hướng

D. Hai vecto u→ và v→ là không cùng phương

Hiển thị lời giải

Giả sử tồn tại số thực k sao cho u→ = k.v→

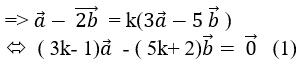
Do hai vecto a→ và b→ không cùng phương nên từ ( 1) suy ra:

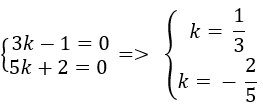
⇒ Không có giá trị nào của k thỏa mãn đầu bài.

⇒ Hai vecto u→ và v→ là không cùng phương.

Chọn D

Câu 2: Cho hai điểm phân biệt A; B và một điểm O bất kỳ không thuộc đường thẳng AB. Mệnh đề nào sau đây là đúng?

A. Điểm M thuộc đường thẳng AB khi và chỉ khi OM→ = OA→ + OB→

B. Điểm M thuộc đường thẳng AB khi và chỉ khi OM→ = OB→ = kBA→

C. Điểm M thuộc đường thẳng AB khi và chỉ khi OM→ = kOA→ + (1-k)OB→

D. Điểm M thuộc đường thẳng AB khi và chỉ khi OM→ = OB→ = k(OB→ - OA→)

Hiển thị lời giải

Chọn C

Câu 3: Cho hình hộp ABCD.A’B’C’D’. Xác định vị trí các điểm M; N lần lượt trên AC và DC’ sao cho MN // BD’. Tính tỉ số MN/BD' bằng?

A. (1/3)                   B. (1/2)                    C. 1                    D. (2/3)

Hiển thị lời giải

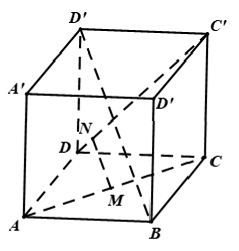
Chọn A

Vậy các điểm M; N được xác định bởi

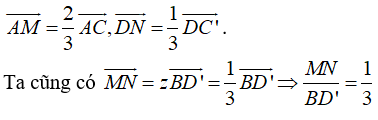
Câu 4: Cho lăng trụ ABC.A’B’C’; gọi I và J lần lượt là trung điểm của AC và A’C’. Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Hỏi vecto nào cùng hướng với vecto IJ→?

A. GG'→                        B. GA'→                        C. AG'→                        D. AB'→

Câu 5: Cho hình chóp S.ABC có M, N, P, Q lần lượt là trung điểm của SC, SB, AB và AC. Tìm mệnh đề đúng?

A. Hai vecto NM→ và BC→ cùng phương và ngược hướng

B. Hai vecto PQ→ và BC→ cùng phương và ngược hướng

C. Hai vecto PQ→ và NM→ cùng phương và ngược hướng

D. Hai vecto QP→ và NM→ cùng phương và ngược hướng .