Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Đường tròn ngoại tiếp tam giác là gì? Các xác định tâm đường tròn ngoại tiếp tam giác, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Đường tròn ngoại tiếp tam giác , các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Đường tròn ngoại tiếp tam giác là gì? Các xác định tâm đường tròn ngoại tiếp tam giác

A. Lý thuyết Đường tròn ngoại tiếp tam giác

• Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác (ta còn nói: tam giác nội tiếp đường tròn)

Khi đó, nối tâm O của đường tròn với ba đỉnh của tam giác ABC ta có: OA = OB = OC là bán kính đường tròn ngoại tiếp tam giác ABC.

• Tính chất:

- Mỗi tam giác có duy nhất một đường tròn ngoại tiếp

- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.

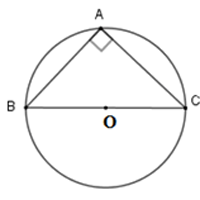
- Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền

- Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng nhau.

Cách để xác định tâm đường tròn ngoại tiếp tam giác

Để có thể xác định được tâm đường tròn ngoại tiếp tam giác, cần chú ý các vấn đề sau:

Thứ nhất, tam giác có 3 đỉnhcách đều 1 điểm thì điểm đó chính là tâm của đường tròn ngoại tiếp tam giác.

Thứ hai, quỹ tích của các điểm nhìn sang đoạn thẳng AB với một số góc vuông sẽ là đường tròn có đường kính AB.

Ta có 2 cách để có thể xác định được tâm của đường tròn ngoại tiếp tam giác là

a, Cách 1:

Bước 1: Gọi K(x;y) là tâm của đường tròn ngoại tiếp tam giác EFJ. Ta có các đoạn thẳng KE = KF = KJ và bằng bán kính R.

Bước 2: Toạ độ tâm K là nghiệm của hệ phương trình

KE ² = KF²

KE² = KJ²

b, Cách 2:

Bước 1: Tìm và viết được các phương trình đường trung trực của hai cạnh trong tam giác bất kỳ.

Bước 2: Sau đó, tìm giao điểm của hai đường trung trực đã tìm ra ở bước 1 và giao điểm của hai đường trung trực chính là tâm đường tròn ngoại tiếp tam giác đó.

Lưu ý: Với tam giác vuông thì tâm của đường tròn ngoại tiếp tam giác này chính là trung điểm của cạnh huyền. Cạnh huyền cũng chính là đường kính của đương tròn ngoại tiếp tam giác đó.

Để có thể xác định được tâm đường tròn ngoại tiếp tam giác theo cách 2, ta cần tìm được phương trình của đường tròn ngoại tiếp tam giác khi biết toạ đô 3 đỉnh. Để có thể giải được bài toán về phương trình đường tròn của ngoại tiếp tam giác ta thực hiện theo các bước như sau:

Hình ảnh minh hoạ đường tròn ngoại tiếp tam giác vuông, với OB là cạnh huyền tam giác ABC, cùng đồng thời là tâm đường tròn O

Bước 1: Đầu tiên ta thay đổi toạ độ mỗi đỉnh của tam giác vào phương trình với ẩn a,b,c (Bởi vì các đỉnh của tam giác thuộc đuòng tròn ngoại tiếp, vì vậy, toạ độ các đỉnh trong tam giác thoả mãn phương trình ngoại tiếp đường tròn mà ta cần tìm

Bước 2: Giải hệ phương trình để tìm ra các hằng số a, b, c tương ứng với các đỉnh trong tam giác

Bước 3: Tiếp theo, ta thay giá trị vừa tìm được như a, b, c vào phương trình tổng quát để tìm ra phương trình đường tròn ngoại tiếp của tam giác.

Bước 4: Do đỉnh của tam giác thuộc đường tròn ngoại tiếp nên ta có hệ phương trình sau, sau khi giải hệ phương trình trên ta sẽ xác định được a, b, c.

Môt số dạng toán nâng cao sẽ yêu cầu các bạn học sinh phải viết được phương trình của đường tròn ngoại tiếp tam giác. Mới nghe qua thì có thể các bạn học sinh sẽ thấy đây là dạng bài khó, tuy nhiên khi nắm vững công thức thì việc giải bài toán này sẽ khá dễ dàng.

B. Bài tập Đường tròn ngoại tiếp tam giác

Bài tập tự luyện

Bài 1: Các đường cao AD, BE của tam giác ABC cắt nhau tại H (góc C khác góc vuông) và cắt đường tròn (O) ngoại tiếp tam giác ABC lần lượt tại I và K.

a) Chứng minh tứ giác CDHE nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác đó.

b) Chứng minh tam giác CKI cân.

Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Ba đường cao của tam giác là AF, BE, CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác.

Bài 3: Cho tam giác ABC vuông tại A có AB < AC, đường cao AH (H thuộc BC). Lấy điểm D sao cho H là trung đểm của BD. Gọi E là chân đường vuông góc hạ từ C xuống đường thẳng AD. Chứng minh tứ giác AHEC nội tiếp và xác định vị trí tâm O của đuờng tròn ngoại tiếp tứ giác đó.

Bài 4: Cho ngũ giác đều có cạnh bằng a

a) Tính chu vi và diện tích ngũ giác đều đó.

b) Tính số đo mỗi góc của ngũ giác đều.

Bài 5: Cho tứ giác ABCD ngoại tiếp đường tròn, biết rằng các tia AB, CD cắt nhau tại E, các tia AD và BC cắt nhau tại F. Chứng minh rằng:

a) AE + CF = AF + CE.

b) BE + BF = DE + DF.

Bài 6: Cho hình thang ABCD (AB // CD) ngoại tiếp đường tròn (O). Tiếp điểm trên AB, CD theo thứ tự là E và F. Chứng minh rằng AC, BD, EF đồng quy.

Bài 7: Tính cạnh hình 12 cạnh đều theo bán kính đường tròn ngoại tiếp hình 12 cạnh đều đó.

Bài 8: Cho đường tròn (O) nội tiếp trong hình thang ABCD (AB // CD) tiếp xúc với cạnh AB tại E với cạnh CD tại F.

a) Chứng minh: $\frac{BE}{AE}=\frac{DF}{CF}$

b) Bết AB = a, CB = b (a < b), BE = 2.AE. Tính diện tích hình thang ABCD.

Bài 9: Cho tam giác ABC ngoại tiếp (O). Trên BC lấy M, trên BA lấy N, trên CA lấy P sao cho B = BN và CM = CP. Chứng minh rằng:

a) O là tâm đường tròn ngoại tiếp tam giác MNP.

b) Tứ giác ANOP nội tiếp đường tròn.

c) Tìm vị trí điểm M, N, P sao cho NP nhỏ nhất.

Bài 10: Cho đường (O; R) nội tiếp hình thang ABCD (AB // CD), với G là tiếp điểm của đyờng tròn (o; R) với các cạnh CD, biết AB = $\frac{4}{3}R$ và BC = $\frac{5}{2}R$. Tính tỉ số giữa GD và GC.