Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Số nguyên tố là gì? Phân tích một số ra thừa số nguyên tố, tài liệu gồm đầy đủ về lý thuyết Số nguyên tố, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Số nguyên tố là gì? Phân tích một số ra thừa số nguyên tố

A. Lý thuyết Số nguyên tố

1. Khái niệm Số nguyên tố

− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Ví dụ:

+ Số 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.

Lưu ý: Số 0 và số 1 không là số nguyên tố cũng không là hợp số.

2. Đặc điểm quan trọng của số nguyên tố

Đặc tính nổi bật của số nguyên tố:

Không bao gồm số 1.

Các số nguyên tố đều không chia hết cho 2 trừ số 2.

Dãy số nguyên tố là vô hạn và không có giới hạn tương tự như tập N.

Ước bé nhất của số bất kỳ thuộc tập N luôn là số nguyên tố. Ví dụ: 15 chia hết cho 3 (ước nhỏ nhất), 3 là số nguyên tố.

Số X có ước nhỏ nhất là số dương, khác 1 và nhỏ hơn căn bậc hai của X thì đó chính là số nguyên tố.

Ví dụ: 30 có ước nhỏ nhất là 5, tính chất của 5 khác 1 và nhỏ hơn căn bậc 2 của 30, nên 5 là số nguyên tố.

3. Bảng số nguyên tố trong toán học

Dãy số nguyên tố không có giới hạn cụ thể vì tính chất vô hạn của số tự nhiên. Tuy nhiên, vẫn có những số phổ biến được sử dụng. Dưới đây là bảng số nguyên tố với các số bé hơn 1000:

2	79	191	311	439	577	709	857
3	83	193	313	443	587	719	859
5	89	197	317	449	593	727	863
7	97	199	331	457	599	733	877
11	101	211	337	461	601	739	881
13	103	223	347	463	607	743	883
17	107	227	349	467	613	751	887
19	109	229	353	479	617	757	907
23	113	233	359	487	619	761	911
29	127	239	367	491	631	769	919
31	131	241	373	499	641	773	929
37	137	251	379	503	643	787	937
41	139	257	383	509	647	797	941
43	149	263	389	521	653	809	947
47	151	269	397	523	659	811	953
53	157	271	401	541	661	821	967
59	163	277	409	547	673	823	971
61	167	281	419	557	677	827	977
67	173	283	421	563	683	829	983
71	179	293	431	569	691	839	991
73	181	307	433	571	701	853	997

 

4. Số nguyên tố cùng nhau là gì?

Số nguyên tố cùng nhau khi UWCLN của 2 số đó là 1. Ví dụ 2 và 3 là số nguyên tố cùng nhau vì chỉ chia hết cho 1. Hoặc 18 và 54 không là số nguyên tố cùng nhau vì chia hết cho 9.

5. Số siêu nguyên tố là gì?

Số siêu nguyên tố là số khi thêm chữ số bên cạnh vẫn là số nguyên tố. Ví dụ 73 là số nguyên tố, thêm số 3 là 733 vẫn là số nguyên tố. Thêm số 7, dạng số 7337 vẫn là số nguyên tố.

6. Cách tìm ra số nguyên tố

Cách 1: Kiểm tra số nguyên tố

Khi kiểm tra số nguyên tố, nếu số đó nhỏ hơn 2 thì đó không phải số nguyên tố.

Khi đếm số ước của số n trong đoạn từ 2 đến căn bậc hai của n mà số đó không có ước nào trong đoạn này thì nó là số nguyên tố. Còn nếu có thì nó đó không phải là số nguyên tố.

Cách 2: Chia thử nghiệm

Cách này được thực hiện bằng cách chia số cần kiểm tra theo lý thuyết số nguyên tố là được, tức là chia n cho tát cả các số nguyên từ 2 đến căn bậc 2 của n. Nếu có bất kỳ số nguyên nào mà n chia hết cho nó thì n là hợp số, còn không có thì n là số nguyên tố.

Đây là phương pháp đơn giản nhưng tốn thời gian, có thể kéo theo nhiều sai số trong quá trình thực hiện vì số phép chia sẻ tăng dần theo cấp số nhân khi số chữ số của số nguyên đó ngày càng nhiều.

Cách 3: Dùng thao tác lập từng phần tử với bước nhảy 1

Để kiểm tra số n có phải số nguyên tố hay không, bạn có thể sử dụng công cụ tính toán - máy tính cầm tay để xác định qua các bước sau:

Bước 1: Nhập vào số n

Bước 2: Kiểm tra nếu n < 2 thì n không phải là số nguyên tố.

Bước 3: Lặp từ 2 tới (n - 1). Nếu trong khoảng này tồn tại số mà n chia hết cho nó thì n không phải là số nguyên tố còn nếu chia hết thì n là số nguyên tố.

Cách 4: Dùng thao tác lặp từng phần tử với bước nhảy 2

Vì 2 là số nguyên tố chẵn duy nhất nên ta sẽ loại số 2 ra khỏi vòng lặp và bạn chỉ cần kiểm tra các số lẻ trong vòng lặp.

B. Lý thuyết Phân tích một số ra thừa số nguyên tố

1. Phân tích một số ra thừa số nguyên tố là gì?

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Chú ý:

   + Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.

   + Mọi hợp số đều phân tích được ra thừa số nguyên tố.

2. Cách phân tích một số ra thừa số nguyên tố

Ta có thể phân tích theo chiều dọc như sau:

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Ví dụ:

 Như vậy 76 = 2².19

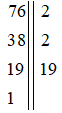
Ví dụ 2: Phân tích các số sau ra thừa số nguyên tố?

a) 450

b) 2100

Ta có:

Vậy 450 = 2.3³.5²

Vậy 2100 = 2².3.5².7

Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào đi nữa thì cuối cùng cũng ra một kết quả.

C. Bài tập Số nguyên tố

1. Bài tập vận dụng

Câu 1. Số nào trong các số sau là số nguyên tố?

A. 3;

B. 8;

C. 12;

D. 15.

Lời giải

Trong các số đã cho:

3 có hai ước là 1 và 3. Do đó 3 là số nguyên tố.

8 có 4 ước là 1; 2; 4; và 8 nên 8 là hợp số.

12 có 6 ước là 1; 2; 3; 4; 6 và 12 nên 12 là hợp số.

15 có 4 ước là 1; 3; 5 và 15 nên 15 là hợp số.

Đáp án: A

Câu 2. Trong các số sau: 16; 17; 20; 21; 23; 97. Có bao nhiêu số là hợp số?

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải

16 có 5 ước là 1; 2; 4; 8; 16 nên 16 là hợp số.

17 có 2 ước là 1 và 17 nên 17 là số nguyên tố.

20 có 6 ước là 1; 2; 4; 5; 10 và 20 nên 20 là hợp số.

21 có 4 ước là 1; 3; 7 và 21 nên 21 là hợp số.

23 có 2 ước là 1 và 23 nên 23 là số nguyên tố.

97 có 2 ước là 1 và 97 nên 97 là số nguyên tố.

Vậy có 3 số là hợp số. 

Đáp án: D

Câu 3. Hoàn thành phát biểu sau: “Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có …”:

A. ước là 1.

B. ước là chính nó.

C. duy nhất một ước.

D. hai ước là 1 và chính nó.

Lời giải Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Đáp án: D

Câu 4. Cho A là tập hợp các số nguyên tố nhỏ hơn 30. Chọn đáp án đúng.

A. 1 ∈ A;

B. 2 ∉ A;

C. 29 ∉ A;

D. 17 ∈ A

Hướng dẫn giải

Lời giải

Các số nguyên tố nhỏ hơn 30 bao gồm: 2; 3; 5; 7; 11; 13; 17; 23; 29.

Do đó A = {2; 3; 5; 7; 11; 13; 17; 23; 29}.

Ta có 1 không thuộc tập A, ta viết 1 ∉ A nên A sai.

Ta có 2 thuộc tập A, ta viết 2 ∈ A nên B sai.

Ta có 29 thuộc tập A, ta viết 29 ∈ A nên C sai.

Ta có 17 thuộc tập A, ta viết 17 ∈ A nên D đúng.

Đáp án: D

Câu 5. Phân tích một số ra thừa số nguyên tố là:

A. phân tích số đó thành tích của số nguyên tố với các hợp số.

B. phân tích số đó thành tích của các số tự nhiên.

C. Phân tích số đó thành tích của các thừa số nguyên tố.

D. Phân tích số đó thành tích của hai thừa số nguyên tố.

Lời giải Phân tích một số ra thừa số nguyên tố là phân tích số đó thành tích của các thừa số nguyên tố.

Đáp án: D

Câu 6. Có bao nhiêu cách để phân tích một số ra thừa số nguyên tố?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải

Lời giải

Có hai cách phân tích một số ra thừa số nguyên tố là: 

+ Phương pháp phân tích theo sơ đồ cây;

+ Phương pháp phân tích theo sơ đồ cột.

Đáp án: B

Câu 7. Có bao nhiêu khẳng định đúng trong các khẳng định sau?

a) Ước nguyên tố của 18 là 1; 2; và 3.

b) Tích của hai số nguyên tố bất kì luôn là số lẻ.

c) Mọi số chẵn đều là hợp số.

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Lời giải

Ước nguyên tố của 18 chỉ có 2 và 3, 1 không phải số nguyên tố nên a sai.

2 là số nguyên tố, 3 là số nguyên tố. Ta có tích 2.3 = 6 là số chẵn nên b sai.

Ta có 2 là số chẵn, 2 cũng là số nguyên tố nên c sai.

Vậy không có phát biểu nào đúng.

Đáp án: A

Câu 8. Tìm chữ số a để 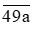là số nguyên tố:

A. 1;

B. 9;

C. A và B đều đúng;

D. cả A và B đều sai.

Lời giải

Dựa vào bảng số nguyên tố ở cuối sách giáo khoa ta có:

491 và 499 là hai số nguyên tố nên a = 1 hoặc a = 9. 

Đáp án: C

Câu 9. Phân tích 70 ra thừa số nguyên tố ta được: 70 = 2^x.5^y.7^z. Tổng x + y + z = ?

A. 3;

B. 4;

C. 5;

D. 6.

Lời giải

Ta có:

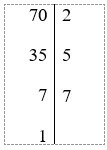
Vậy 70 = 2.5.7.

Suy ra x = 1; y = 1; z = 1.

Do đó x + y + z = 1 + 1 + 1 = 3.

Đáp án: A

Câu 10. Hoàn thành sơ đồ cây sau:

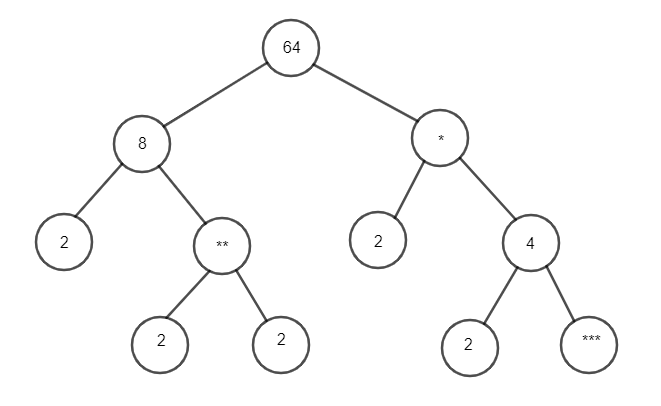
A. * = 8; ** = 2; *** = 4.

B. * = 4; ** = 8; *** = 2.

C. * = 8; ** = 4; *** = 2.

D. * = 4; ** = 2; *** = 8.

Lời giải

Sơ đồ cây hoàn chỉnh là: 

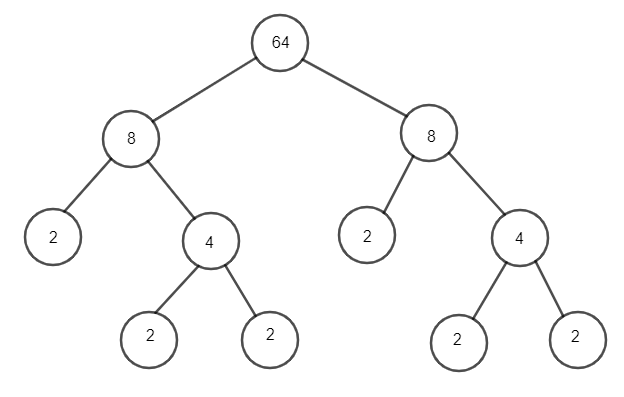
Vậy * = 8; ** = 4; *** = 2.

Đáp án: C

Câu 11. Phân tích số 75 ra thừa số nguyên tố là:

A. 75 = 3.25;

B. 75 = 15.5;

C. 75 = 3.5²;

D. 75 = 75.1.

Lời giải: Ta có:

Suy ra 75 = 3.5².

Đáp án: C

Lời giải

Ta có: 

Suy ra 75 = 3.5².

Chọn C.

Câu 12. Bạn Nam phân tích số 120 ra thừa số nguyên tố như sau: 120 = 2³.3.5.

Bạn An phân tích 105 ra thừa số nguyên tố như sau: 105 = 3.5.7.

Chọn đáp án đúng.

A. Bạn Nam; 

B. Bạn An;

C. Cả Nam và An đều sai.

D. Cả Nam và An đều đúng.

Lời giải

Ta có:

120 60 30 15 5 1

2 2 2 3 5

Vậy 120 = 2³.3.5. Do đó Nam đúng.

Ta có

105 35 7 1

3 5 7

Vậy 105 = 3.5.7. Do đó An đúng.

Đáp án: D

Câu 13. Hãy phân tích A = 4².9⁵ ra thừa số nguyên tố.

A. A = 4².9⁵.

B. A = 2⁴.9⁵.

C. A = 4².3¹⁰.

D. A = 2⁴.3¹⁰

Lời giải A = 4².9⁵ = 4.4.9.9.9.9.9 = 2.2.2.2.3.3.3.3.3.3.3.3.3.3 = 2⁴.3¹⁰.

Đáp án: D

Câu 14. Chọn câu sai:

A. 504 = 2³.3².7.

B. 102 = 2.3.17.

C. 75 = 2.5².

D. 170 = 2.5.17.

Lời giải

504 252 126 63 21 7 1

2 2 2 3 3 7

Vậy 504 = 2³.3².7 nên A đúng.

102 51 17

2 3 17

Vậy 102 = 2.3.17 nên B đúng

75 25 5 1

3 5 5

Vậy 75 = 3.5² nên C sai.

170 85 17 1

2 5 17

Vậy 170 = 2.5.17 nên D đúng.

Đáp án: C

Câu 15. Tìm các số còn thiếu trong sơ đồ phân tích một số ra thừa số nguyên tố sau:

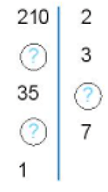
Các số cần điền từ lần lượt từ trên xuống dưới là:

A. 105; 5 và 7.

B. 105; 7 và 5.

C. 150; 5 và 7.

D. 150; 7 và 5.

Lời giải

+) Ta có 210 : 2 = 105

                    105 : 3 = 35

                    35 : 5 = 7

                    7 : 7 = 1

Ta hoàn thiện sơ đồ:             

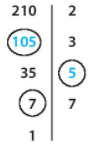
Vậy các số còn thiếu lần lượt từ trên xuống dưới là: 105; 5 và 7.

Đáp án: A

2. Bài tập tự luyện

Bài 1. Trong các khẳng định dưới đây, khẳng định nào là đúng?

A. 84 = 2.3.7;

B. 84 = 2².3.7;

C. 84 = 2.3².7;

D. 84 = 3.5.7.

Đáp án đúng là: B

Ta có:

Suy ra: 84 = 2².3.7.

Bài 2. Trong các khẳng định dưới đây, khẳng định nào là đúng?

A. 140 = 2².5.7;

B. 140 = 2.5.7;

C. 140 = 2.5².7;

D. 140 = 3.5.7.

Đáp án đúng là: A

Ta có:

Suy ra: 140 = 2².5.7.

Bài 3. Cho số a = 2.3³.7 . Khẳng định nào dưới đây là đúng?

A. 2; 6; 8; 9; 21 là ước của a.

B. 2; 8; 9; 21; 63 là ước của a.

C. 2; 6; 8; 21; 63 là ước của a.

D. 2; 6; 9; 21; 63 là ước của a.

Đáp án đúng là: D

Các số 2; 6 (= 2.3); 9 (= 3²); 21 (= 3.7); 63 (= 3².7) đều là ước của a nhưng 8 không là ước của a.

Bài 4. Cho số a = 3².5. Các ước của a là:

A. 1; 3; 5; 9; 15; 45.

B. 1; 2; 5; 9; 15; 45.

C. 1; 3; 6; 9; 15; 45.

D. 1; 3; 5; 12; 15; 45.

Đáp án đúng là: A

Các ước của 3² là 1; 3; 9.

Các ước của 5 là 1; 5.

Lần lượt lấy từng ước của 5 nhân với từng ước của 3², ta được các ước của a là: 1; 3; 5; 9; 15; 45.

Bài 5. Bạn Huyền có 50 cái kẹo, Huyền muốn chia đều số kẹo cho các em nhỏ. Hỏi Huyền có thể chia đều số kẹo đó cho bao nhiêu em (Kể cả trường hợp chia hết 50 cái kẹo cho 1 em)?

A. 1; 2; 5; 10; 25; 40.

B. 1; 2; 5; 10; 25; 50.

C. 1; 2; 3; 10; 25; 50.

D. 1; 2; 5; 15; 25; 50.

Đáp án đúng là: B

Muốn chia đều số kẹo cho các em nhỏ thì số em phải là ước của 50.

Ta có: 50 = 2.5²; suy ra Ư(50) = {1; 2; 5; 10; 25; 50}

Vậy Huyền có thể chia đềo số kẹo đó cho 1 em; 2 em, 5 em, 10 em, 25 em hoặc 50 em.

Bài 6. Tập hợp ước số của 1000 có số phần tử là:

A. 16;

B. 15;

C. 12;

D. 18.

Đáp án đúng là: A

Ta có: 1000 = 2³.5³

Các ước của 2³ là: 1; 2; 4; 8;

Các ước của 5³ là: 1; 5; 25; 125;

Lần lượt lấy từng ước của 5³ nhân với từng ước của 2³, ta được ước của 1000 là:

{1; 2; 4; 8; 5; 10; 20; 40; 25; 50; 100; 200; 125; 250; 500; 1000}.

Bài 7. Hiền có 24 chiếc bút màu, Hiền muốn xếp chúng vào các hộp nhỏ sao cho số bút ở mỗi hộp bằng nhau và bằng một số lớn hơn 2. Hỏi Hiền có thể xếp vào nhiều nhất bao nhiêu hộp?

A. 9;

B. 6;

C. 7;

D. 8.

Đáp án đúng là: D

Số hộp có thể xếp được là ước của 24.

Ta có: 24 = 2³.3 suy ra Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.

Vì số bi ở mỗi hộp lớn hơn 2 nên có thể xếp được vào nhiều nhất 8 hộp.

Bài 8. Ba số tự nhiên liên tiếp mà tích của chúng là 46620 là:

A. 33; 34; 35;

B. 34; 35; 36;

C. 32; 33; 34;

D. 35; 36; 37.

Đáp án đúng là: D

Ta có: 46 620 = 2².3².5.7.37 = (5.7).(2².3²).37 = 35.36.37.

Vậy ba số tự nhiên liên tiếp cần tìm là 35, 36, 37.

Bài 9. Ba số lẻ liên tiếp có tích bằng 12 075 là

A. 19; 20; 21.

B. 19; 21; 23.

C. 21; 25; 27.

D. 21; 23; 25.

Đáp án đúng là: D

Ta có: 12075 = 3.5².7.23 = (3.7).23.(5²) = 21.23.25.

Vậy ba số lẻ liên tiếp cần tìm là: 21, 23, 25.

Bài 10. Cho số tự nhiên n thỏa mãn: 1 + 2 + 3 + 4 + ... + n = 465. Giá trị của n là:
A. 30;

B. 31;

C. 32;

D. 33.

Đáp án đúng là: A

Ta có: 1 + 2 + 3 + 4 + … + n = $\frac{n(n+1)}{2}$ = 465.

Do đó: n(n + 1) = 930.

Mà 930 = 2.3.5.31 = (2.3.5).31 = 30.31.

Vậy n  = 30.

3. Bài tập nâng cao

Câu 1: Tìm bốn số nguyên tố liên tiếp, sao cho tổng của chúng là số nguyên tố.

Lời giải:

Tổng của 4 số nguyên tố là một số nguyên tố ⇒ tổng của 4 số nguyên tố là 1 số lẻ ⇒ trong 4 số đó tồn tại ít nhất một số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2. Vậy 4 số nguyên tố cần tìm là: 2; 3; 5; 7

Câu 2: Tổng của hai số nguyên tố có thể bằng 2003 được không?

Lời giải:

Vì tổng của 2 số nguyên tố bằng 2003, nên trong 2 số nguyên tố đó tồn tại 1 số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2. Do đó số nguyên tố còn lại là 2001. Do 2001 chia hết cho 3 và 2001 > 3. Suy ra 2001 không phải là số nguyên tố. ⇒ Tổng của hai số nguyên tố không thể bằng 2003 .

Câu 3: Tìm hai số nguyên tố, sao cho tổng và hiệu của chúng đều là số nguyên tố.

Lời giải:

Gọi a, b, c, d là các số nguyên tố. (a>b)

Từ (*) ⇒ a > 2, a là số nguyên tố lẻ ⇒ c + b và d – b là số lẻ. Do b, c, d đều là số nguyên tố nên để c + b và d – b là số lẻ thì ⇒ b chẵn. Vậy b = 2

a. Bài toán đưa về dạng tìm một số nguyên tố a sao cho a – 2 và a + 2 cũng là số nguyên tố.

- Nếu a = 5 ⇒ a – 2 = 3; a + 2 = 7 đều là số nguyên tố

- Nếu a ≠ 5 . Xét 2 trường hợp

   + a chia 3 dư 1 ⇒ a + 2 chia hết cho 3 : không là số nguyên tố

   + a chia 3 dư 2 ⇒ a – 2 chia hết cho 3: không là số nguyên tố

Vậy chỉ có số nguyên tố a duy nhất thoả mãn là 5.

Hai số nguyên tố cần tìm là 5; 2

Câu 4: Tìm số nguyên tố có ba chữ số, biết rằng nếu viết số đó theo thứ tự ngược lại thì ta được một số là lập phương của một số tự nhiên.

Lời giải:

Gọi số tự nhiên đó là a.

Ta có 103 = 1000; 53 = 125 ⇒ 125 ≤ a 3 < 1000 ⇒ 5 ≤ a < 10

Ta có bảng sau:

a	5	6	7	8	9
a3	125	216	343	512	729
Số cần tìm	521	612	343	215	927
Kết luận	TM	loại	loại	loại	loại

Vậy số cần tìm là 521

Câu 5: Cho p là số nguyên tố lớn hơn 3. Biết p + 2 cũng là số nguyên tố. Chứng minh rằng p + 1 chia hết cho 6.

Lời giải:

Vì p là số nguyên tố lớn hơn 3 nên p có dạng 6k-1 hoặc 6k+1nếu p=6k+1 thì p+2=6k+3=3(2k+1)chia hết cho 3 và lớn hơn 3 nên là hợp số(vô lí) do đó p=6k-1⇒p+1=6k chia hết cho 6(đpcm)

Câu 6: Một số nguyên tố p chia cho 42 có số dư r là hợp số. Tìm số dư r.

Lời giải:

Ta có:

p = 42.k + r. = 2.3.7.k + r

Vì r là hợp số và r < 42 nên r phải là tích của 2 số r = x.y

x và y không thể là 2, 3, 7 và cũng không thể là số chia hết cho 2, 3, 7 được vì nếu thế thì p không là số nguyên tố.

Vậy x và y có thể là các số trong các số {5,11,13, ..}

Nếu x=5 và y=11 thì r = x.y =55 > 42

Vậy chỉ còn trường hợp x = 5, y = 5. Khi đó r = 25

Câu 7: Hai số nguyên tố sinh đôi là hai số nguyên tố hơn kém nhau 2 đơn vị. Tìm hai số nguyên tố sinh đôi nhỏ hơn 50.

Lời giải:

Các số nguyên tố sinh đôi nhỏ hơn 50 là:3 và 5; 5 và 7; 11 và 13; 17 và 19; 29 và 31; 41 và 43.

Câu 8: Tìm số nguyên tố, biết rằng số đó bằng tổng của hai chữ số nguyên tố và bằng hiệu của hai số nguyên tố.

Lời giải:

Giả sử a, b, c, d, e là các số nguyên tố (d > e)

Theo bài ra ta có: a = b + c = d – e (*)

Từ (*) ⇒ a > 2 ⇒ a là số nguyên tố lẻ

   + b + c = d – e là số lẻ.do b, d là các số nguyên tố ⇒ b, d là số lẻ ⇒ c, e là số chẵn.

   + c = e = 2 (do e, c là các số nguyên tố)

   + a = b + 2 = d – 2 ⇒ d = b + 4,vậy ta cần tìm số nguyên tố b sao cho b + 2, b + 4 cũng là số nguyên tố

   + b = 3

Vậy số nguyên tố cần tìm là 5