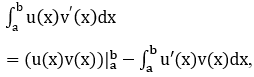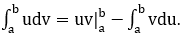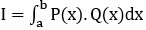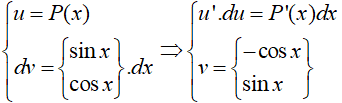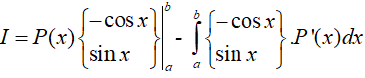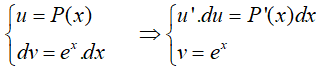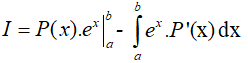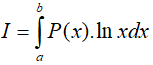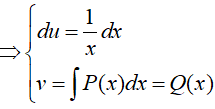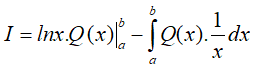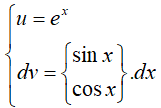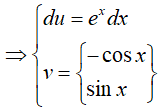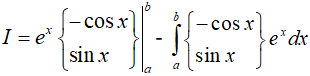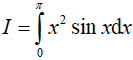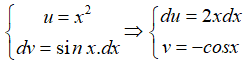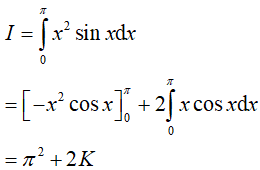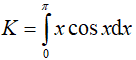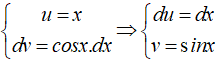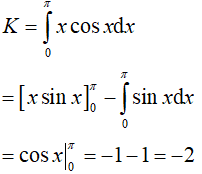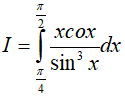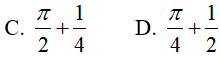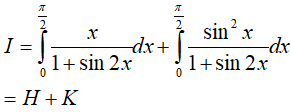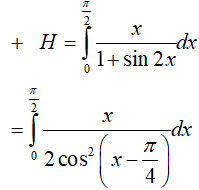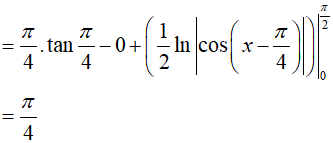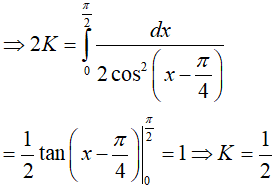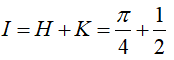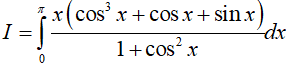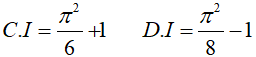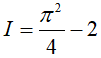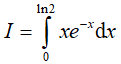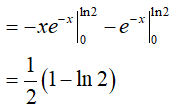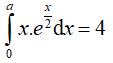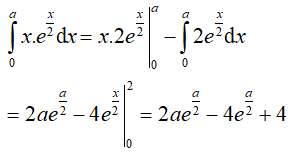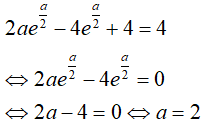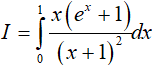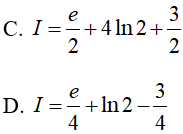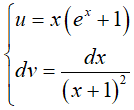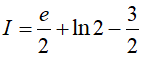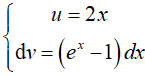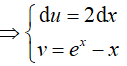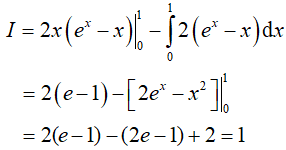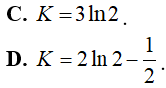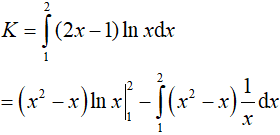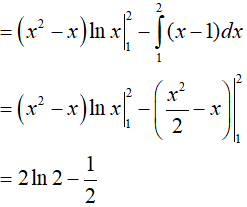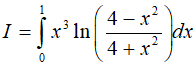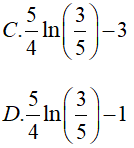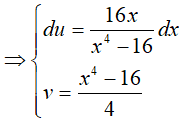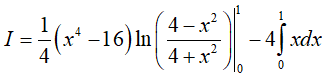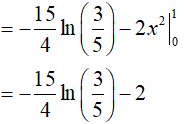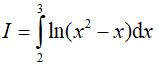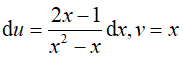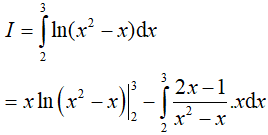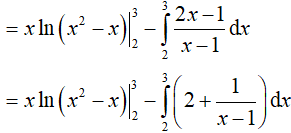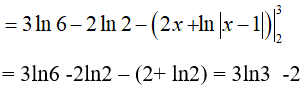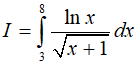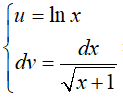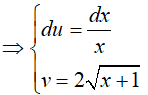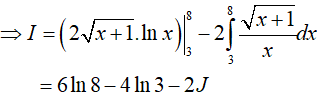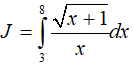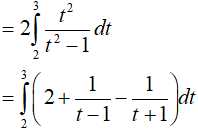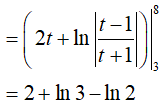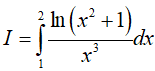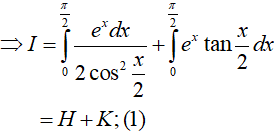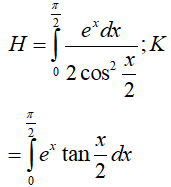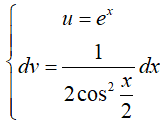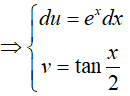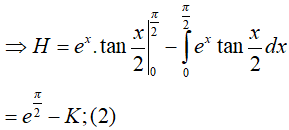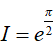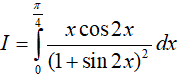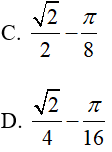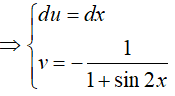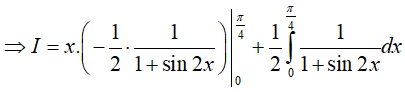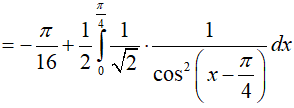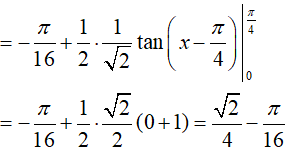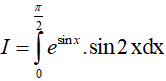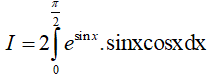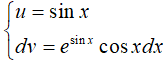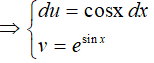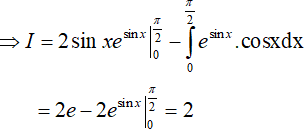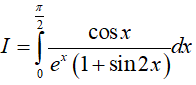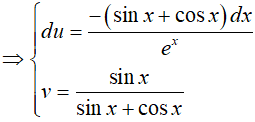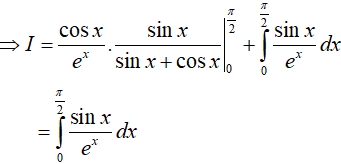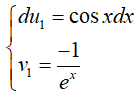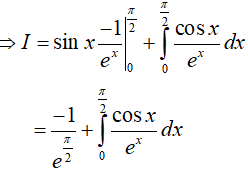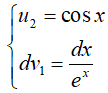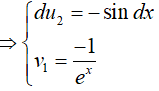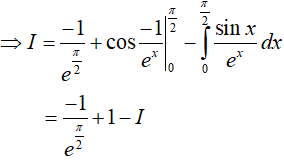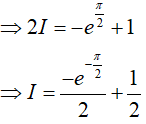Tailieumoi.vn xin giới thiệu tới bạn đọc tài liệu về Tích phân từng phần là gì? Phương pháp tính tích phân từng phần, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Tích phân từng phần, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Tích phân từng phần là gì? Phương pháp tính tích phân từng phần
A. Lý thuyết Tích phân từng phần
Định lí: Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm và liên tục trên đoạn [a;b] thì
hay viết gọn là 
Các dạng cơ bản: Giả sử cần tính 
| Dạng hàm |
P(x): Đa thức Q(x): sin(kx) hay cos(kx) |
P(x): Đa thức Q(x):ekx |
P(x): Đa thức Q(x):ln(ax+b) |
P(x): Đa thức Q(x): 1/(sin2x) hay 1/(cos2x) |
| Cách đặt |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
* u = ln(ax+b) * dv = P(x)dx |
* u = P(x) * dv là Phần còn lại của biểu thức dưới dấu tích phân |
Thông thường nên chú ý: “Nhất log, nhì đa, tam lượng, tứ mũ”.
B. Bài tập Tích phân từng phần
Các dạng toán thường gặp
Dạng 1. Tích phân có dạng: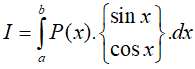 
trong đó P(x) là đa thức
Phương pháp giải
Đặt
Vậy
Dạng 2. Tích phân có dạng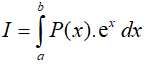 
trong đó P(x) là đa thức
Phương pháp giải
Đặt 
Vậy 
Dạng 3. Tích phân có dạng: 
Phương pháp giải
Đặt 
Vậy 
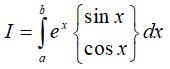.Phương pháp giải
Đặt 
Vậy 
Bằng phương pháp tương tự ta tính được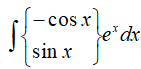 
sau đó thay vào I.
Bài tập vận dụng
Bài 1. Tính 
A. π2 − 4 B. π2 + 4 C. 2π2 − 3 D. 2π2 + 3
Lời giải:
Đáp án: A
*Đặt 
Khi đó:
Đặt 
Khi đó:
Vậy: I = π2 + 2(−2) = π2 − 4
Bài 2. Tính 
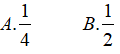
Lời giải:
Đáp án: B
Ta có
Đặt 
Bài 3. Tính 
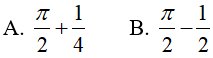
Lời giải:
Đáp án: C
Ta có
Đặt
Đặt 
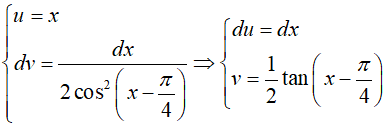
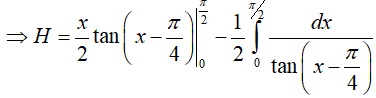
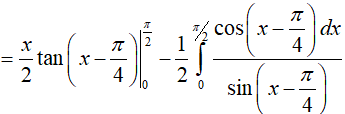
Vậy 
Bài 4. Tính 
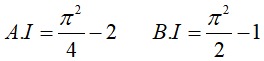
Lời giải:
Đáp án: C
Ta có:
+ Tính 
Đặt 
+ Tính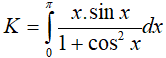 
Đặt x = π − t => dx = −dt
Đặt t = cosx => dt = −sinx.dx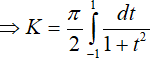 
, đặt t = tanu => dt = (1 + tan2u)du
Vậy 
Bài 5. Tích phân 
Lời giải:
Đáp án: A
Đặt u = x; dv = e−x.dx, suy ra du = dx; v = −e−x
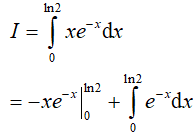
Bài 6. Tìm a > 0 sao cho 
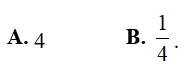
Lời giải:
Đáp án: D
Đặt u = x, 
, suy ra du = dx, 
Theo giả thiết ta có:
Bài 7. Tính 
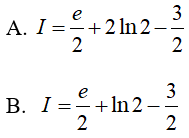
Lời giải:
Đáp án: B
Đặt 
Vậy 
Bài 8. Tính 
A. 0 B.1 C. 2 D. 3
Lời giải:
Đáp án: B
Ta có 
Đặt 
Bài 9. Tích phân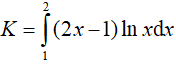 
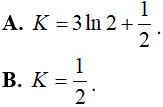
bằng:
Lời giải:
Đáp án: D
Đặt u = lnx, dv = (2x − 1)dx suy ra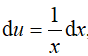 
, v = x2 − x
Bài 10. Tính 
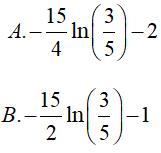
Lời giải:
Đáp án: A
Đặt 
Do đó
Bài 11. Tính 
A. 3ln3 B. 2ln3 C. 3ln3 − 2. D. 2 − 3ln3.
Lời giải:
Đáp án: C
Đặt u = ln(x2 − x); dv = dx
Suy ra:
Bài 12. Tính 
A. 20ln2 − 6ln3 − 4 B. 10ln2 + ln3 − 1
C. 12ln2 + 2ln3 − 3 D.10 ln 3 − 2ln 2 − 3
Lời giải:
Đáp án: A
Đặt 
Tính 
Đặt t = √(x + 1)
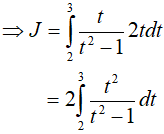
Từ đó I = 20 ln2 − 6ln 3 − 4
Bài 13. Tính 
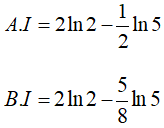
Lời giải:
Đáp án: B
Đặt 
Do đó
Bài 14. Tính 
Lời giải:
Đáp án: A
Ta có:
Trong đó
* Ta tính H
Đặt: 
Từ (1) và (2) suy ra, 
Bài 15. Tính 
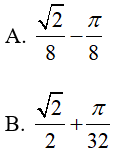
Lời giải:
Đáp án: D
Đặt 
Bài 16. Tính 
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: B
Đặt 
Bài 17. Tính 
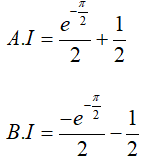
Lời giải:
Đáp án: D
Đặt 
Đặt 
Đặt 
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
