Sơ đồ Hoocne: Cách sử dụng lược đồ Hoocne và bài tập vận dụng

Van Anh Ngày: 13-11-2024 Tổng hợp kiến thức

Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Sơ đồ Hoocne: Cách sử dụng lược đồ Hoocne và bài tập vận dụng, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Sơ đồ Hoocne, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Sơ đồ Hoocne: Cách sử dụng lược đồ Hoocne và bài tập vận dụng

A. Lý thuyết Lược đồ Hoocne

Sơ đồ Horner (Hoocne/ Hoắc - le/ Hắc - le) dùng để tìm đa thức thương và dư trong phép chia đa thức f(x) cho đa thức x - α , khi đó ta thực hiện như sau:

Giả sử cho đa thức

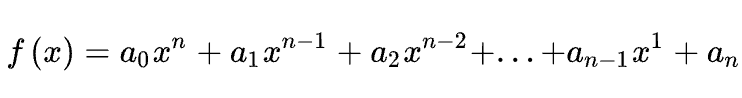
Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Khi đó đa thức thương $g(x) = b_{0} x^{n-1} + b_{1} x^{n-2} + .... + b_{n-1}$ và đa thức dư được xác định theo lược đồ sau:

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Ta được cách làm theo các bước như sau:

Bước 1: Sắp xếp các hệ số của đa thức f(x) theo ẩn giảm dần và đặt số $\alpha$ vào cột đầu tiên của hàng thứ 2. Nếu trong đa thức mà khuyết ẩn nào đó thì ta coi hệ số của nó bằng 0 và vẫn phải điền vào lược đồ.

Bước 2: Cột thứ 2 của hàng 2 ta hạ hệ số a0 ở hàng trên xuống. Đây chính là hệ số đầu tiên của g(x) tìm được, tức là $b_{0}$ .

Bước 3: Lấy số $\alpha$ nhân với hệ số vừa tìm được ở hàng 2 rồi cộng chéo với hệ số hàng 1 (Ví dụ nếu ta muốn tìm hệ số b1 ở hàng thứ hai, trước tiên ta sẽ lấy $\alpha$ nhân với hệ số b0 sau đó cộng với hệ số a1 ở hàng trên; tương tự như vậy nếu ta muốn tìm hệ số b2 ở hàng thứ hai, trước tiên ta sẽ lấy $\alpha$ nhân với hệ số b1 sau đó cộng với hệ số a2 ở hàng trên,….)

Quy tắc nhớ: NHÂN NGANG, CỘNG CHÉO.

Bước 4: Cứ tiếp tục như vậy cho tới hệ số cuối cùng và kết quả ta sẽ có

$f(x) = (x - \alpha ). g(x) + r$

hay

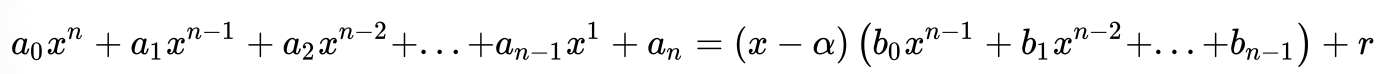
Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

* Chú ý:

+ Bậc của đa thức g(x) luôn nhỏ hơn bậc của đa thức f(x) 1 đơn vị vì đa thức chia x- a có bậc là 1.

+ Nếu r = 0 thì đa thức f(x) chia hết cho đa thức g(x) và x = a sẽ là một nghiệm của đa thức f(x). Trong trường hợp này chính là phân tích đa thức thành nhân tử. Để tìm được $\alpha$ , ta sẽ nhẩm một nghiệm nguyên của đa thức f(x), $\alpha$ chính là nghiệm mà ta vừa nhẩm được.

B. Bài tập Lược đồ Hoocne

Bài tập vận dụng

Bài 1: Kết quả của phép chia ( 7x³- 7x + 42 ):( x² - 2x + 3 ) là ?

A. - 7x + 14 B. 7x + 14C. 7x - 14 D. - 7x - 14

Lời giải:

Ta có phép chia

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Chọn đáp án B.

Bài 2: Phép chia x³ + x²- 4x + 7 cho x² - 2x + 5 được đa thức dư là ?

A. 3x - 7. B. - 3x - 8.

C. - 15x + 7. D. - 3x - 7.

Lời giải

Ta có pchiai

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Dựa vào kết quả của phép chia trên,, ta có đa thức dư là - 3x - 8.

Chọn đáp án B.

Bài 3: Hệ số a thỏa mãn để 4x² - 6x + a chia hết có x - 3 là ?

A. a = - 18. B. a = 8.

C. a = 18. D. a = - 8.

Lời giải:

Ta có phép chia

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Phép chia trên có số dư là ( a + 18 )

Để 4x²- 6x + a chia hết có x - 3 ⇔ a + 18 = 0 ⇔ a = - 18.

Chọn đáp án A.

Bài 4: Thực hiện phép chia: (4x⁴ + x + 2x³ - 3x²) : (x²+ 1) ta được số dư là :

A. – x + 7

B. 4x2 + 2x - 7

C. 4x2 – 2x + 7

D. x – 7

Lời giải:

Ta có: 4x⁴+ x + 2x³- 3x² = 4x⁴ + 2x³ – 3x² + x

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Vậy: (4x⁴ + x + 2x³ - 3x²) = (4x² + 2x – 7 ).(x² +1) – x + 7

Chọn đáp án A

Bài 5: Thực hiện phép chia (3x³+ 2x + 1 ) : (x + 2) ta được đa thức dư là :

A. 10 B. -9

C. – 15 D. – 27

Lời giải:

Ta có:

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Vậy số dư của phép chia đã cho là –27

Chọn đáp án D

Bài 6: Thực hiện phép chia (-4x⁴ + 5x² + x ) : (x² + x) ta được kết quả là:

A. – 4x⁴+ 5x²+ x = (x² + x).(-4x² - 4x + 9) - 6x

B. – 4x⁴ + 5x² + x = (x² + x).(4x² + 4x + 9) + 12x

C. – 4x⁴+ 5x² + x = (x² + x).(-4x² + 4x + 9) - 8x

D. – 4x⁴+ 5x2 + x = (x² + x). ( 4x² - 4x + 9) + 10x

Lời giải:

Ta có:

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Vậy –4x⁴+ 5x² + x = (x² + x).(-4x² + 4x + 9) - 8x

Chọn đáp án C

Bài 7: Cho phép chia: (x³ + 9x² + 27x + 27) : (x + 3). Tìm khẳng định sai?

A. Đây là phép chia hết

B. Thương của phép chia là: (x + 3)²

C. Thương của phép chia là: x² + 6x + 9

D. Số dư của phép chia là: x – 3 .

Lời giải:

Áp dụng hằng đẳng thức đáng nhớ:

(a + b)³ = a³ + 3a²b + 3ab² + b³ta được:

(x³ + 9x² + 27x + 27) : (x + 3) = (x + 3)³ : (x + 3) = (x + 3)² = x² + 6x +9

Vậy phéo chia đã cho là phép chia hết có thương là: (x + 3)² = x² + 6x + 9.

Chọn đáp án D

Bài 8: Thực hiện phép chia: (x²y + 4xy + 3y ) : (x + 1) ta được thuơng là:

A. xy + 3 B. x + 3y

C. x + y + 3 D. y. (x + 3)

Lời giải:

Ta có: x²y + 4xy + 3y = y.(x² + 4x + 3)

= y.[(x² + x ) + (3x + 3)]

= y.[x.(x + 1) + 3(x + 1)]

= y.(x + 3).(x+1 )

Vậy: (x²y + 4xy + 3y ) : (x + 1) = y.(x + 3).(x + 1) : (x + 1) = y.(x + 3).

Chọn đáp án D

Bài 9: Tìm a để phép chia (x³– 4x + a): (x – 2) là phép chia hết:

A. a = 0 B. a = 4

C. a = -8 D. a = 8

Lời giải:

Ta có:

Sử dụng sơ đồ Hoocne (Horner) để chia đa thức dễ hiểu nhất

Để phép chia đã cho là phép chia hết khi và chỉ khi phần dư bằng 0. Do đó, a =0

Chọn đáp án A

Bài 10: Làm tính chia: (9x³y²+ 10x⁴y⁵ - 8x²y²) : x²y²

A. 9x + 10x²y² B. 9 + 10x²y² - 8

C. 9x + 10x²y³ – 8 D. Đáp án khác

Lời giải:

Ta có: (9x³y² + 10x⁴y⁵ - 8x²y²) : x²y²

= 9x³y² : x²y² + 10x⁴y⁵ : x²y² - 8x²y² : x²y²

= 9x + 10x²y³- 8

Chọn đáp án C

Bài tập tự luyện

Bài 1: Phân tích các đa thức sau thành nhân tử:

a, ${x^3} - 4{x^2} + x + 6$ $x^{3} - 4 x^{2} + x + 6$

b, ${x^3} - 5{x^2} - 2x + 24$ $x^{3} - 5 x^{2} - 2 x + 24$

c, $2{x^4} - {x^3} - 17{x^2} + x + 15$ $2 x^{4} - x^{3} - 17 x^{2} + x + 15$

d, $3{x^4} + 5{x^3} - 5{x^2} - 5x + 2$ $3 x^{4} + 5 x^{3} - 5 x^{2} - 5 x + 2$

Bài 2: Thực hiện phép chia đa thức:

a, ${x^5} + 6{x^4} + 3{x^2} - 2x - 10$ $x^{5} + 6 x^{4} + 3 x^{2} - 2 x - 10$ cho $x + 8$

b, $2{x^7} - 8{x^5} + 3{x^3} - 9{x^2} - 10x + 1$ $2 x^{7} - 8 x^{5} + 3 x^{3} - 9 x^{2} - 10 x + 1$ cho $x - 5$

c, ${x^4} + 12{x^2} - 25$ $x^{4} + 12 x^{2} - 25$ cho $2 x + 5$

d, ${x^5} - 7{x^4} + 8{x^3} - 4{x^2} - 10x + 13$ $x^{5} - 7 x^{4} + 8 x^{3} - 4 x^{2} - 10 x + 13$ cho $x + 1$

Bài 3: Giải các phương trình sau:

a, $2{x^4} - 5{x^3} + 6{x^2} - 5x + 2 = 0$ $2 x^{4} - 5 x^{3} + 6 x^{2} - 5 x + 2 = 0$

b, $\left( {x + 2} \right)\left( {x - 3} \right)\left( {x + 4} \right)\left( {x - 6} \right) + 6{x^2} = 0$ $(x + 2) (x - 3) (x + 4) (x - 6) + 6 x^{2} = 0$

c, $\left( {{x^2} + x + 2} \right)\left( {{x^2} + x + 3} \right) = 6$ $(x^{2} + x + 2) (x^{2} + x + 3) = 6$

d, $2{x^4} - 21{x^3} + 34{x^2} + 105x + 50 = 0$ $2 x^{4} - 21 x^{3} + 34 x^{2} + 105 x + 50 = 0$

Bài 4: Thực hiện phép chia:

a) $\left(-3 x^{3}+5 x^{2}-9 x+15\right):(-3 x+5)$ $(- 3 x^{3} + 5 x^{2} - 9 x + 15) : (- 3 x + 5)$

b) $\left(5 x^{4}+9 x^{3}-2 x^{2}-4 x-8\right):(x-1)$ $(5 x^{4} + 9 x^{3} - 2 x^{2} - 4 x - 8) : (x - 1)$

c) $\left(5 x^{3}+14 x^{2}+12 x+8\right):(x+2);$ $(5 x^{3} + 14 x^{2} + 12 x + 8) : (x + 2);$

d) $\left(x^{4}-2 x^{3}+2 x-1\right):\left(x^{2}-1\right).$ $(x^{4} - 2 x^{3} + 2 x - 1) : (x^{2} - 1) .$

Bài 5: Làm phép chia bằng cách áp dụng hằng đẳng thức:

a) $\left(x^{8}-2 x^{4} y^{4}+y^{8}\right):\left(x^{2}+y^{2}\right)$ $(x^{8} - 2 x^{4} y^{4} + y^{8}) : (x^{2} + y^{2})$

b) $\left(64 x^{3}+27\right):\left(16 x^{2}-12 x+9\right)$ $(64 x^{3} + 27) : (16 x^{2} - 12 x + 9)$

c) $\left(x^{3}-9 x^{2}+27 x-27\right):\left(x^{2}-6 x+9\right)$ $(x^{3} - 9 x^{2} + 27 x - 27) : (x^{2} - 6 x + 9)$

d) $\left(x^{3} y^{6} z^{9}-1\right):\left(x y^{2} z^{3}-1\right).$ $(x^{3} y^{6} z^{9} - 1) : (x y^{2} z^{3} - 1) .$

Bài 6: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi làm phép chia:

a) $\left(13 x+41 x^{2}+35 x^{3}-14\right):(5 x-2) ;$ $(13 x + 41 x^{2} + 35 x^{3} - 14) : (5 x - 2);$

b) $\left(16 x^{2}-22 x+15-6 x^{3}+x^{4}\right):\left(x^{2}-2 x+3\right)$ $(16 x^{2} - 22 x + 15 - 6 x^{3} + x^{4}) : (x^{2} - 2 x + 3)$

c) $\left(6 x+2 x^{3}-5-11 x^{2}\right):\left(-x+2 x^{2}+1\right).$ $(6 x + 2 x^{3} - 5 - 11 x^{2}) : (- x + 2 x^{2} + 1) .$

Bài 7 Tìm m đề đa thức $3 x^{3}+2 x^{2}-7 x+m$ $3 x^{3} + 2 x^{2} - 7 x + m$ chia hết cho đa thức 3x-1

Bài 8 Tìm số dư trong phép chia đa thức $f(y)=y^{243}+y^{81}+y^{27}+y^{9}+y^{3}+y$ $f (y) = y^{243} + y^{81} + y^{27} + y^{9} + y^{3} + y$ cho đa thức
$g(y)=y^{2}-1$