Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Cách viết Phương trình mặt phẳng trung trực của đoạn thẳng và bài tập vận dụng, tài liệu bao gồm có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Cách viết Phương trình mặt phẳng trung trực của đoạn thẳng và bài tập vận dụng

1. Mặt phẳng trung trực là gì?

Trước tiên chúng ta cùng ôn lại khái niệm mặt phẳng trung trực của đoạn thẳng (đã học từ lớp 11).

Trong không gian cho đoạn thẳng AB và điểm I là trung điểm của AB. Khi đó tồn tại duy nhất một mặt phẳng (P) đi qua I và vuông góc với đoạn thẳng AB. Mặt phẳng (P) được gọi là mặt phẳng trung trực của đoạn thẳng AB.

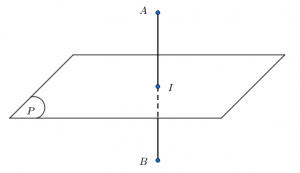
Nếu phát biểu dưới dạng quỹ tích thì mặt phẳng trung trực là quỹ tích các điểm cách đều hai điểm cho trước.

Như vậy chúng ta có thể thấy khái niệm mặt phẳng trung trực cũng tương tự như khái niệm đường trung trực của đoạn thẳng trong mặt phẳng.

2. Cách viết phương trình mặt phẳng trung trực của đoạn thẳng

Từ định nghĩa nêu trên ta có thể thấy rằng nếu (P) là mặt phẳng trung trực của đoạn AB. Thì véc tơ AB chính là 1 véc tơ pháp tuyến của mặt phẳng (P). Còn trung điểm I của đoạn AB chính là 1 điểm nằm trên mặt phẳng (P).

Do đó cách viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB như sau:

Bước 1: Tính véc tơ AB là một véc tơ pháp tuyến của mặt phẳng (P). (Cách tính véc tơ AB là lấy tọa độ điểm cuối B trừ đi tọa độ điểm đầu A tương ứng).

Bước 2: Tìm tọa độ điểm I là trung điểm của đoạn thẳng AB. (Cách tìm tọa độ trung điểm là lấy tọa độ điểm A cộng tọa độ điểm B tương ứng, xong chia cho 2)

Bước 3: Viết phương trình mặt phẳng (P) đi qua điểm I nhận véc tơ AB là véc tơ pháp tuyến.

Ví dụ minh họa (Tự luận):

Trong không gian Oxyz, cho điểm A(1;2;3) và điểm B(3;6;1). Biết mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của (P).

Lời giải:

Trung điểm I của đoạn thẳng AB có tọa độ là (2;4;2).

Véc tơ AB có tọa độ (2;4;−2) là một véc tơ pháp tuyến của mặt phẳng (P).

Do đó phương trình mặt phẳng (P) là:

2(x−2)+4(y−4)−2(z−2)=0

⇔2x+4y−2z−16=0

⇔x+2y−z−8=0.

Ví dụ minh họa (Trắc nghiệm):

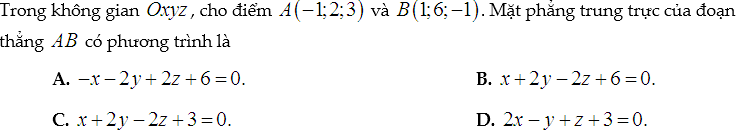
Lời giải:

Trung điểm I của đoạn thẳng AB có tọa độ là (0;4;1).

Véc tơ AB có tọa độ (2;4;−4) là một véc tơ pháp tuyến của mặt phẳng trung trực của đoạn AB.

Vậy mặt phẳng cần tìm có phương trình là:

2(x−0)+4(y−4)−4(z−1)=0

⇔x+2y−2z−6=0

⇔−x−2y+2z+6=0.

Chọn đáp án A.

3. Cách nhẩm nhanh phương trình mặt phẳng trung trực

Thông thường khi tính toán viết ptmp trung trực ta thường lược bớt các bước biến đổi để cho ra kết quả ngay. Ta xét lại ví dụ bên trên:

“Trong không gian Oxyz, cho điểm A(1;2;3) và điểm B(3;6;1). Biết mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của (P).”

Ta sẽ tiến hành nhẩm véc tơ AB=(2;4;-2). Khi đó ta sẽ viết được “phần đầu” của phương trình là:

2x+4y-2z+….=0

Đến đây ta nhẩm tọa độ trung điểm AB là I(2;4;2) ta thay luôn vào “phần đầu” phương trình vừa tìm được. Bài nào phân số hay số to ta có thể dùng chức năng CALC của máy tính để tính.

Ta được: 2.2+4.4-2.2=16. Ta lấy “phần đầu” trừ đi 16 (kết quả vừa nhẩm được) là được kết quả:

2x+4y-2z-16=0

4. Bài tập vận dụng

Bài tập 1: Trong không gian $Oxyz$, cho $A(-1;-1;1)$, $B(3;1;1)$. Phương trình mặt phẳng trung trực của đoạn $AB$ là.

Lời giải

Gọi $I$ là trung điểm của $AB$ nên $I(1;0;1)$.

Mặt phẳng trung trực của đoạn $AB$có vtpt là $\overrightarrow{n}$$=\overrightarrow{AB}$$=(4;2;0)$$=2(2;1;0)$.

Phương trình mặt phẳng cần tìm là: $2(x-1)+1(y-0)=0$$\iff 2x+y-2=0$.

Bài tập 2:

Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1;6;-7)$ và $B(3;2;1)$. Phương trình mặt phẳng trung trực đoạn $AB$ là.

Lời giải

Mặt phẳng trung trực đoạn $AB$ đi qua trung điểm $I(2;4;-3)$ của đoạn $AB$ và nhân $\overrightarrow{AB}=(2;-4;8)$ làm vectơ pháp tuyến có phương trình:

$2(x-2)-4(y-4)+8(z+3)=0$$\iff x-2y+4z+18=0$

Bài tập 3:

Trong không gian $Oxyz$, cho hai điểm $A(1;3;-4)$ và $B(-1;2;2)$. Viết phương trình mặt phẳng trung trực $\left(\alpha \right)$ của đoạn thẳng$AB$.

A. $\left(\alpha \right):4x+2y+12z+7=0$.                                 B. $\left(\alpha \right):4x-2y+12z+17=0$.

C. $\left(\alpha \right):4x+2y-12z-17=0$.                                 D. $\left(\alpha \right):4x-2y-12z-7=0$.

Lời giải

Gọi $I(0;\frac{5}{2};-1)$ là trung điểm của $AB$; $\overrightarrow{AB}=(-2;-1;6)$.

Mặt phẳng $\left(\alpha \right)$ qua $I(0;\frac{5}{2};-1)$ và có VTPT $\overrightarrow{n}=(-2;-1;6)$ nên có PT:$\left(\alpha \right):-2\left(x\right)-(y-\frac{5}{2})+6(z+1)=0\iff 4x+2y-12z-17=0$.

Đáp án: C

Bài tập 4:

Trong không gian $Oxyz$, cho hai điểm $A(1;-1;2)$ và $B(3;3;0)$. Mặt phẳng trung trực của đoạn thẳng $AB$ có phương trình là

A. $x+y-z-2=0$.                 B. $x+y-z+2=0$.            C. $x+2y-z-3=0$.              D. $x+2y-z+3=0$.

Lời giải

Ta có $\overrightarrow{AB}=2(1;2;-1)$.

Gọi $I$ là trung điểm của $AB\Rightarrow I(2;1;1)$.

+ Mặt phẳng trung trực$\left(\alpha \right)$ của đoạn thẳng $AB$ đi qua $I$và nhận $\overrightarrow{n}=\frac{1}{2}\overrightarrow{AB}=(1;2;-1)$ làm vectơ pháp tuyến có phương trình là

$x-2+2(y-1)-(z-1)=0\iff x+2y-z-3=0$.

Vậy mặt phẳng trung trực của đoạn thẳng $AB$ là $x+2y-z-3=0$.

Đáp án: C.

Bài tập 5:

Trong không gian với hệ tọa độ$Oxyz$, cho điểm $A(2;4;1);B(-1;1;3)$ và mặt phẳng $\left(P\right):x-3y+2z-5=0$. Một mặt phẳng $\left(Q\right)$ đi qua hai điểm $A,B$ và vuông góc với mặt phẳng $\left(P\right)$ có dạng $ax+by+cz-11=0$. Khẳng định nào sau đây là đúng?

A. $a+b+c=5$.            B. $a+b+c=15$.               C. $a+b+c=-5$.              D. $a+b+c=-15$.

Lời giải

Vì $\left(Q\right)$ vuông góc với $\left(P\right)$ nên $\left(Q\right)$ nhận vtpt $\overrightarrow{n}=(1;-3;2)$của $\left(P\right)$làm vtcp

Mặt khác $\left(Q\right)$đi qua $A$ và $B$ nên $\left(Q\right)$nhận $\overrightarrow{AB}=(-3;-3;2)$ làm vtcp

$\left(Q\right)$ nhận $\overrightarrow{n_Q}=[\overrightarrow{n},\overrightarrow{AB}]=(0;8;12)$ làm vtpt

Vậy phương trình mặt phẳng $\left(Q\right):0(x+1)+8(y-1)+12(z-3)=0$, hay $\left(Q\right):2y+3z-11=0$

Vậy $a+b+c=5$.

Đáp án: A.

Bài tập 6:

Trong không gian với hệ tọa độ $Oxyz$, cho $A(1;-1;2);B(2;1;1)$ và mặt phẳng $\left(P\right):x+y+z+1=0$. Mặt phẳng $\left(Q\right)$ chứa $A,B$ và vuông góc với mặt phẳng $\left(P\right)$. Mặt phẳng $\left(Q\right)$ có phương trình là:

A. $3x-2y-z-3=0$.                B. $x+y+z-2=0$.                C. $-x+y=0$.                D. $3x-2y-z+3=0$.

Lời giải

Ta có $\overrightarrow{AB}=(1;2;-1)$

Từ $\left(P\right)$ suy ra vec tơ pháp tuyến của $\left(P\right)$ là $\overrightarrow{n_P}=(1;1;1)$

Gọi vec tơ pháp tuyến của $\left(Q\right)$ là $\overrightarrow{n_Q}$

Vì $\left(Q\right)$ chứa $A,B$ nên $\overrightarrow{n_Q}\mathrm{\perp }\overrightarrow{AB}\left(1\right)$

Mặt khác $\left(Q\right)\mathrm{\perp }\left(P\right)$ nên $\overrightarrow{n_Q}\mathrm{\perp }\overrightarrow{n_P}\left(2\right)$

Từ $\left(1\right),\left(2\right)$ ta được $\overrightarrow{n_Q}=[\overrightarrow{AB},\overrightarrow{n_P}]=(3;-2;-1)$

$\left(Q\right)$ đi qua $A(1;-1;2)$ và có vec tơ pháp tuyến $\overrightarrow{n_Q}=(3;-2;-1)$ nên $\left(Q\right)$ có phương trình là

$3(x-1)-2(y+1)-(z-2)=0$ $\iff 3x-2y-z-3=0$.

Vậy $a+b+c=5$.

Đáp án: A

Bài tập 7:

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left(P\right):x+y+z+1=0$ và hai điểm $A(1;-1;2);B(2;1;1)$. Mặt phẳng $\left(Q\right)$ chứa $A,B$ và vuông góc với mặt phẳng $\left(P\right)$, mặt phẳng $\left(Q\right)$có phương trình là:

A. $3x-2y-z+3=0$.                B. $x+y+z-2=0$.                C. $3x-2y-z-3=0$.                D. $-x+y=0$.

Lời giải

Mặt phẳng $\left(P\right)$ có 1 véc tơ pháp tuyến là $\overrightarrow{n_p}=(1;1;1)$. Véc tơ $\overrightarrow{AB}=(1;2;-1)$.

Gọi $\overrightarrow{n}$ là một véc tơ pháp tuyến của $\left(Q\right)$, do $\left(Q\right)$vuông góc với $\left(P\right)$ nên $\overrightarrow{n}$có giá vuông góc với $\overrightarrow{n_p}$, mặt khác véc tơ $\overrightarrow{AB}$ có giá nằm trong mặt phẳng $\left(Q\right)$ nên $\overrightarrow{n}$ cũng vuông góc với $\overrightarrow{AB}$

Mà ${\overrightarrow{n}}_p$ và $\overrightarrow{AB}$ không cùng phương nên ta có thể chọn $\overrightarrow{n}$=$[\overrightarrow{n_P},\overrightarrow{AB}]=(-3;2;1)$, mặt khác $\left(Q\right)$đi qua $A(1;-1;2)$ nên phương trình của mặt phẳng $\left(Q\right)$ là:

$-3(x-1)+2(y+1)+1(z-2)=0\iff 3x-2y-z-3=0$.

Đáp án: C.

Bài tập 8:

Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;1;1)$ và hai mặt phẳng $\left(P\right):2x-y+3z-1=0$, $\left(Q\right):y=0$. Viết phương trình mặt phẳng $\left(R\right)$ chứa $A$, vuông góc với cả hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$.

A. $3x-y+2z-4=0$.                B. $3x+y-2z-2=0$.                C. $3x-2z=0$.                D. $3x-2z-1=0$.

Lời giải

$\left(P\right):2x-y+3z-1=0$ có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(P\right)}=(2;-1;3)$.

$\left(Q\right):y=0$ có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(Q\right)}=(0;1;0)$.

Do mặt phẳng $\left(R\right)$ vuông góc với cả hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$ nên có véctơ pháp tuyến ${\overrightarrow{n}}_{\left(R\right)}=[{\overrightarrow{n}}_{\left(P\right)},{\overrightarrow{n}}_{\left(Q\right)}]$. $\Rightarrow {\overrightarrow{n}}_{\left(R\right)}=(-3;0;2)$.

Vậy phương trình mặt phẳng $\left(R\right)$ là: $-3x+2z+1=0$$\iff 3x-2z-1=0$.

Đáp án: D