Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Trọng tâm tam giác: Định nghĩa, tính chất và các dạng bài tập, tài liệu gồm đầy đủ về lý thuyết Trọng tâm tam giác, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Trọng tâm tam giác: Định nghĩa, tính chất và các dạng bài tập

A. Lý thuyết Trọng tâm tam giác

1. Khái niệm

Trọng tâm của tam giác chính là giao điểm của 3 đường trung tuyến. 

 Đường trung tuyến của một tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện.

Ví dụ: Cho tam giác ABC với AM, BN, CP lần lượt là 3 đường trung tuyến xuất phát từ 3 đỉnh A, B, C.

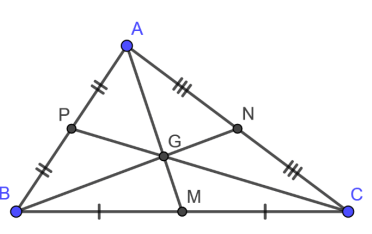
Khi đó, các đường trung tuyến AM, BN, CP cắt nhau tại điểm G. Vì vậy, G chính là trọng tâm của tam giác ABC đã cho.

2. Tính chất trọng tâm tam giác

Tính chất trọng tâm của tam giác được phát biểu như sau:

Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyển đi qua đỉnh ấy.

Cho tam giác ABC, với AM là đường trung tuyến và G là trọng tâm tam giác:

Áp dụng tính chất trọng tâm của tam giác, ta có: $\frac{AG}{AM}=\frac{2}{3}$.

Do đó: $\frac{GM}{AM}=\frac{1}{3};\frac{GM}{GA}=\frac{1}{2}$.

Quy tắc trọng tâm tam giác theo vectơ

Trọng tâm tam giác là giao điểm của ba đường trung tuyến. Áp dụng quy tắc trọng tâm tam giác:

Điểm G là trọng tâm tam giác ABC thì ta có: 

 với mọi điểm M bất kỳ.

Với từng dạng tam giác đặc biệt, tính chất trọng tâm của tam giác được biểu thị như sau:

Trong tam giác vuông

Giả sử tam giác MNP vuông tại M. 3 đường trung tuyến MD, NE, PF giao nhau tại trọng tâm O. Ta có MD là trung tuyến của góc vuông PMN nên MD = 1/2 PN = DP = DN.

Trọng tâm tam giác cân

Giả sử tam giác ABC cân tại A, có G là trọng tâm. Vì tam giác ABC cân tại A nên AG vừa là đường trung tuyến, đường cao và là đường phân giác.

Do vậy ta suy ra được hệ quả của trọng tâm tam giác cân ABC như sau:

• Góc BAD bằng góc CAD.
• Trung tuyến AD vuông góc với cạnh đáy BC.

Trọng tâm của tam giác vuông cân

Giả sử tam giác ABC vuông cân tại A và I là trọng tâm. AM là đường trung trực, đường trung tuyến và đường cao của tam giác này nên AM vuông góc với BC. Mặt khác, vì tam giác ABC vuông cân tại A nên ta suy ra:

AB = AC. => BP = CN và BN = AN = CP = AP.

Trọng tâm tam giác đều

Giả sử cho tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác. Theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

Ví dụ 1. Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G.

a) Chứng minh BD = CE;

b) Chứng minh tam giác GBC là tam giác cân.

Hướng dẫn giải

a) Ta có DABC cân tại A nên AB = AC.

mà AB = 2BE; AC = 2CD (vì E, D theo thứ tự là trung điểm của AB, AC).

Do đó 2BE = 2CD hay BE = CD.

Xét DBCE và DCBD có:

BE = CD (chứng minh trên);

$\widehat{EBC}=\widehat{DCB}$;

BC là cạnh chung.

Do đó $∆$BCE = $∆$CBD (c.g.c).

Suy ra CE = BD (hai cạnh tương ứng)

b) G là trọng tâm tam giác ABC nên ta có:

$BG=\frac{2}{3}BD$ và $CG=\frac{2}{3}CE$ (tính chất trọng tâm).

Mà CG = BG.

Vậy tam giác GBC cân tại G.

Ví dụ 2. Cho tam giác ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Vẽ điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm của BD.
Chứng minh ba điểm A, G, E thẳng hàng.

Hướng dẫn giải

Xét tam giác ABD có C là trung điểm của cạnh AD

Suy ra BC là trung tuyến của tam giác ABD.

Hơn nữa G ∈ BC và BG = 2GC.

Suy ra $GB=\frac{2}{3}BC$.

Do đó, G là trọng tâm tam giác ABD.

Lại có AE là đường trung tuyến của tam giác ABD nên A, G, E thẳng hàng.

Vậy ba điểm A, G, E thẳng hàng.

3. Cách xác định trọng tâm tam giác

Cách 1: Dựa vào khái niệm trọng tâm tam giác là giao điểm 3 đường trung tuyến, ta xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.

Bước 1: Vẽ tam giác ABC, lần lượt xác định trung điểm của các cạnh AB, BC, CA.

Bước 2: Nối lần lượt các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E.

Bước 3: Giao điểm I của ba đường trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.

Cách 2: Dựa vào tính chất về tỉ lệ các đoạn trên đường trung tuyến, ta xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến như sau:

Bước 1: Vẽ tam giác ABC, xác định trung điểm M của cạnh BC.

Bước 2: Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM. Theo tính chất trọng tâm tam giác thì điểm S chính là trọng tâm tam giác ABC.

B. Bài tập Trọng tâm tam giác

1. Bài tập vận dụng

Bài 1: Chọn câu sai:

A. Trong một tam giác có ba đường trung tuyến

B. Các đường trung tuyến của tam giác cắt tại một điểm

C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó

D. Một tam giác có hai trọng tâm

Lời giải:

Một tam giác chỉ có một trọng tâm nên D sai.

Chọn đáp án D.

Bài 2: Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”

A. 2/3       

B. 3/2     

C. 3       

D. 2

Lời giải:

Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy

Số cần điền là 2/3.

Chọn đáp án A.

Bài 3: Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: BG = ....BE

A. 2       

B. 3             

C. 1/3           

D. 2/3

Lời giải:

Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Theo tính chất ba đường trung tuyến của tam giác ta có:

Vậy số thích hợp điền vào chỗ chấm là: 2/3

Chọn đáp án D.

Bài 4: Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: AG = ....GD

A. 2            

B. 3             

C. 1/3             

D. 2/3

Lời giải:

Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC .

Theo tính chất ba đường trung tuyến của tam giác ta có:

Vậy số thích hợp điền vào chỗ chấm là: 2

Chọn đáp án A.

Bài 5: Tam giác ABC có trung tuyến AM = 9cm và trọng tâm G. Độ dài đoạn AG là:

A. 4,5cm            

B. 3cm            

C. 6cm            

D. 4cm

Lời giải:

Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến nên AG = (2/3)AM (tính chất ba đường trung tuyến của tam giác)

Do đó: AG = (2/3).9 = 6cm

Chọn đáp án C.

Bài 6: Cho ΔABC cân. Biết AB = AC = 10cm, BC = 12cm. M là trung điểm B

C. Độ dài trung tuyến AM là:

A. 22cm.

B. 4cm.

C. 8cm.

D. 6cm.

Lời giải:

Chọn đáp án C

Bài 7: Cho ΔABC có M là trung điểm của BC. G là trọng tâm của tam giác và AG = 12cm. Độ dài đoạn thẳng AM =?

A. 18cm.

B. 16cm.

C. 14cm.

D. 13cm.

Lời giải:

M là trung điểm của BC nên AM là đường trung tuyến kẻ từ A của tam giác ABC

Mà G là trọng tâm của tam giác ABC

Do đó:

Vậy AM = 18 cm.

Chọn đáp án A

Bài 8: Cho ΔABC vuông tại A. Nếu AM là đường trung tuyến thì:

A. AM ⊥ BC

B. AM = MC.

C. M trùng với đỉnh A.

D. M nằm ở trong ΔABC

Lời giải:

+ Ta có AM là trung tuyến thì M là trung điểm cạnh BC, nên M ≠ A nên C sai.

+ Tương tự M nằm trên cạnh BC nên M không nằm trong tam giác ABC, nên D sai.

+ AM ⊥ BC khi tam giác ABC là tam giác cân (Theo chứng minh ở câu 6), nên A sai.

Vậy B là đáp án đúng.

Ta chứng minh B đúng như sau:

Trên tia đối của tia MA lấy điểm D sao cho MA = MD

Xét tam giác AMB và tam giác DMC, ta có:

MA = MD (ta dựng)

MB = MC (M là trung điểm BC)

Chọn đáp án B

Bài 9: Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D và E sao cho AD = DE = EM. Gọi O là trung điểm của đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là:

A. Điểm D

B. Điểm E

C. Điểm O

D. Cả A, B, C đều sai

Lời giải:

Ta có: D, E, O thuộc trung tuyến AM

Mà AD = DE = EM; O là trung điểm của DE

Nên AD = 1/3 AM; AE = 2/3 AM;

O là trung điểm của AM

Khi đó E là trọng tâm của tam giác ABC

(khoảng cách từ đỉnh tới trọng tâm của tam giác bằng 2/3 độ dài đường trung tuyến kẻ từ đỉnh đó).

Chọn đáp án B

Bài 10: Cho tam giác ABC có G là trọng tâm, đường trung tuyến AD. Trên tia đối của tia DA lấy điểm M sao cho DM = 1/3 AD. Khẳng định nào là đúng trong số các khẳng định dưới đây?

A. D là trung điểm của GM.

B. G là trung điểm của AD.

C. AD = 3/4 GM.

D. AG = 3DM.

Lời giải:

Chọn đáp án A

2. Bài tập tự luyện

Bài 1. Cho tam giác ABC cân ở A, đường trung tuyến AM.

a) Chứng minh AM ⊥ BC.

b) Tính AM biết rằng AB = 10 cm, BC = 12 cm.

Bài 2. Cho tam giác ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Chứng minh GX = GY = GZ.

Bài 3. Cho tam giác ABC có hai đường trung tuyến AD và BE vuông góc với nhau tại G. Biết AD = 4,5 cm; BE = 6 cm. Tính độ dài AB.

Bài 4. Chứng minh rằng trong tam giác tổng độ dài ba đường trung tuyến nhỏ hơn chu vi nhưng lớn hơn $\frac{3}{4}$ chu vi tam giác đó.

Bài 5. Cho tam giác ABC, D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC.

a) Chứng minh G là trọng tâm tam giác EFC.

b) Tính các tỉ số $\frac{GE}{GK};\frac{GC}{DC}$.