Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Hình thang cân là gì? Tính chất hình thang cân, các công thức về hình thang cân đầy đủ, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Hình thang cân, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Hình thang cân là gì? Tính chất hình thang cân, các công thức về hình thang cân

A. Lý thuyết Hình thang cân

1. Định nghĩa

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Tứ giác ABCD là hình thang cân ( đáy AB, CD). Khi đó, ta có  hoặc 

2. Tính chất

- Trong hình thang cân hai cạnh bên bằng nhau.

Hình thang ABCD (AB//CD) cân suy ra AD = BC

- Trong hình thang cân hai đường chéo bằng nhau.

Hình thang ABCD (AB//CD) cân suy ra AC = BD

3. Dấu hiệu nhận biết

- Hình thang có hai góc kề một đáy là hình thang cân.

- Hình thang có hai đường chéo bằng nhau là hình thang cân.

Lưu ý: Hình thang cân thì có hai cạnh bên bằng nhau nhưng hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân. Ví dụ như hình vẽ dưới đây:

4. Diện tích hình thang cân

Để tính diện tích hình thang cân ta áp dụng công thức tính diện tích hình thang như thông thường.

Diện tích hình thang bằng chiều cao nhân với trung bình cộng của hai đáy.

    

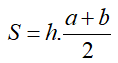
“ Muốn tính diện tích hình thang

Đáy lớn, đáy bé ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi kết quả thế nào cũng ra”

5. Chu vi hình thang cân

Giả sử hình thang ABCD (AB//CD) cân có độ dài hai cạnh đáy là a, b và độ dài cạnh bên là c.

Khi đó, chu vi hình thang ABCD là:

P = a + b + 2c

B. Các dạng bài tập Hình thang cân

Dạng 1. Tính số đo góc

Phương pháp giải: Sử dụng tính chất hai đường thẳng song song và tổng bốn góc trong một tứ giác kết hợp với kiến thức đã học về hình thang, hình thang cân, hình thang vuông.

Ví dụ 1: Cho hình thang ABCD có AB // CD, 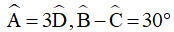. Tính số đo các góc của hình thang.

Lời giải:

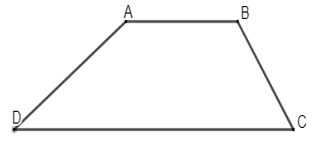
Vì AB // CD nên ta có

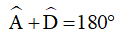 (hai góc trong cùng phía)

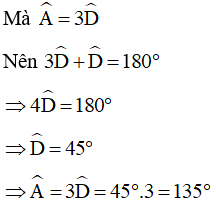
Vì AB // CD nên ta có:

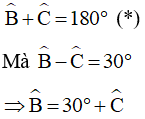
Thay vào (*) ta được:

 

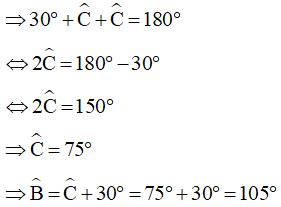
Ví dụ 2: Cho hình thang cân ABCD có AB // CD. Biết 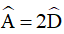. Tính các góc của hình thang.

Lời giải

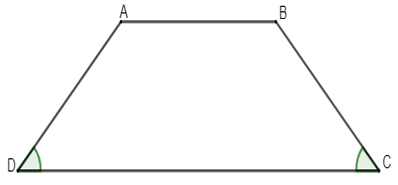
Vì AB // CD ta có:

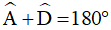 (hai góc trong cùng phía)

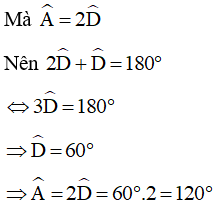
Mà ABCD là hình thang cân nên ta có:

 

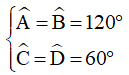
Dạng 2. Chứng minh hình thang, hình thang cân hình thang vuông

Phương pháp giải: Sử dụng định nghĩa hình thang, hình thang cân, hình thang vuông.

Ví dụ 1: Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân.

Lời giải:

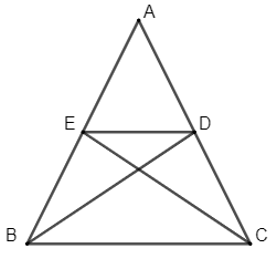
Vì BD là đường trung tuyến của tam giác ABC nên D là trung điểm của AC.

 

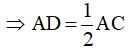
Vì CE là đườg trung tuyến của tam giác ABC nên E là trung điểm của AB

 

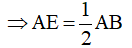
Mà AB = AC (do tam gác ABC cân tại A)

Do đó: AD = AE

Xét tam giác AED có

AD = AE ( chứng minh trên)

Do đó: cân tại A 

Ta có:

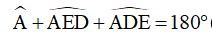 (tổng ba góc trong một tam giác)

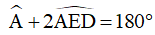 (do tam giác AED cân tại A nên  )

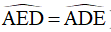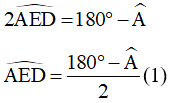
Lại có: cân tại A nên:

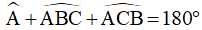 (tổng ba góc trong một tam giác)

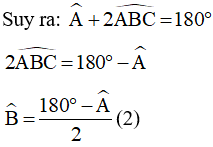
Từ (1) và (2) =>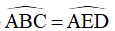 

Mà hai góc này ở vị trí đồng vị nên ED //BC

=> Tứ giác BCDE là hình thang

Mặt khác: cân tại  A nên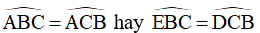 

Vậy hình thang BCDE là hình thang cân (do có hai góc kề một đáy bằng nhau).

Ví dụ 2: Cho tam giác ABC vuông cân tại A. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tứ giác ABCD là hình gì? Vì sao?

Lời giải:

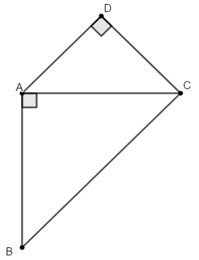
Vì tam giác ABC là tam giác vuông cân tại A

 

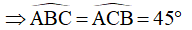
Vì tam giác ADC là tam giác vuông cân tại D

 

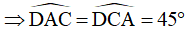
Do đó: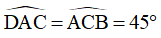  

Mà 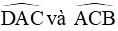 là hai góc so le trong

Do đó: AD // BC 

Xét tứ giác ABCD ta có:

 

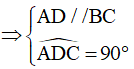
Suy ra ABCD là hình thang vuông.

Dạng 3. Sử dụng các tính chất của hình thang, hình thang cân, hình thang vuông để chứng minh bài toán.

Phương pháp giải: Áp dụng các tính chất về cạnh và góc của hình thang, hình thang cân, hình thang vuông  đã học để giải quyết bài toán

Ví dụ 1: Cho hình thang vuông ABCD có 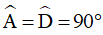, AB = AD , DC = 2AB và BE vuông góc với CD tại E.

a) Chứng minh: ΔABD = ΔEDB 

b) Chứng minh: ΔBEC vuông cân tại E.

Lời giải:

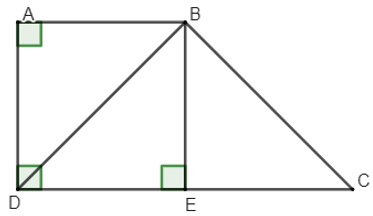
a) Do ABCD là hình thang nên AB // CD => 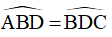 (hai góc so le trong)

Vì BE vuông góc với DC =>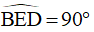 

Xét ΔABD và tam giác ΔEDB ta có:

BD chung

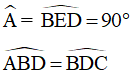
Do đó: ΔABD = ΔEDB (cạnh huyền - góc nhọn)

b) Từ hai tam giác bằng nhau ở câu a ta có:

AB = ED; AD = EB (các cặp cạnh tương ứng)

Mà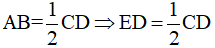  

Suy ra E là trung điểm của CD

=> ED = AB = EC

Mà AB = AD (giả thuyết)

Nên ED = AB = EC = AD = EB 

Xét tam giác BEC có

EB = EC

 

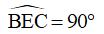
Vậy ΔBEC là tam giác vuông cân tại E

Ví dụ 2: Cho hình thang cân ABCD có  AB // CD, AB < CD. Gọi G là giao điểm của AD và BC. Gọi F là giao điểm của AC và BD. Chứng minh:

a) Tam giác AGB cân tại G;

b) Các tam giác ABD và BAC bằng nhau;

c) FC = FD.

Lời giải:

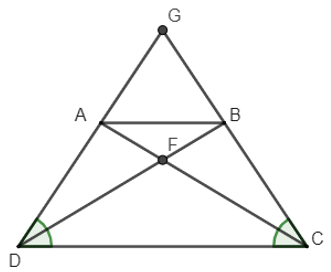
a) Vì AB // CD nên ta có:

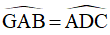 (hai góc đồng vị)

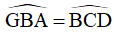 (hai góc đồng vị)

Mà 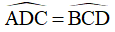 (do ABCD là hình thang cân)

Do đó: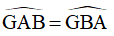  

Xét tam giác AGB có:

 

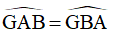
Nên tam giác AGB là tam giác cân tại G.

b) Xét hai tam giác ABD và BAC có:

AB chung

AD = BC (do ABCD là hình thang cân)

AC = BD (do ABCD là hình thang cân)

Do đó: ΔABD = ΔBAC (c – c – c)

c) Ta có:

 

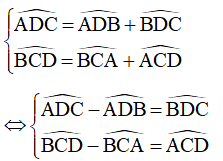
Mà 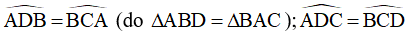 (ABCD là hình thang cân)

Do đó: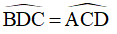  

Xét tam giác FCD có:

 

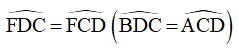
Suy ra tam giác FCD cân tại F

 FC = FD (điều phải chứng minh)

C. Bài tập Hình thang cân

1. Bài tập vận dụng

Bài 1. Tính số đo các góc chưa biết của hình thang IJGH (IJ // GH) trong các trường hợp sau:

a) $\hat{H}=50°$ , $\hat{J}=110°$ .

b) IJGH là hình thang cân và $\hat{H}=30°$ .

c) $\hat{H}=90°$ , $\hat{G}=50°$ .

Hướng dẫn giải

a)

Do IJ // GH nên ta có:

$\hat{I}+\hat{H}=180°$, suy ra $\hat{I}=180°-\hat{H}=180°-50°=130°$

$\hat{J}+\hat{G}=180°$, suy ra $\hat{G}=180°-\hat{J}=180°-110°=70°$

Vậy hình thang IJGH có: $\hat{I}=130°$; $\hat{G}=70°$.

b)

Hình thang cân IJGH (IJ // GH) có $\hat{I}=\hat{J}$ và $\hat{G}=\hat{H}=30°$ (tính chất hình thang cân).

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{I}+\hat{J}+\hat{G}+\hat{H}=360°$

Suy ra $2\hat{I}=360°-2\hat{H}=360°-2.30°=300°$

Do đó $\hat{I}=\hat{J}=150°$ .

Vậy hình thang cân IJGH có: $\hat{G}=30°$; $\hat{I}=\hat{J}=150°$.

c)

$\hat{H}=90°$ nên hình thang IJGH là hình thang vuông, suy ra $\hat{H}=\hat{I}=90°$

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{J}=360°-\left(\hat{I}+\hat{G}+\hat{H}\right)=360°-\left(90°+50°+90°\right)=360°-230°=130°$

Vậy hình thang vuông IJGH có: $\hat{I}=90°$ , $\hat{J}=130°$ .

Bài 2. Cho hình thang cân ABCD (AB // CD). Hai tia phân giác của A và B cắt nhau tại điểm K nằm trên cạnh đáy DC. Từ K kẻ đoạn thẳng KM vuông góc với AB tại M.

a) Chứng minh ∆ABK là tam giác cân.

b) Chứng minh AM = BM.

Hướng dẫn giải

a) Do AK là tia phân giác của $\hat{A}$ nên $\widehat{DAK}=\widehat{KAB}=\frac{\widehat{DAB}}{2}$.

BK là tia phân giác của $\hat{B}$ nên $\widehat{CBK}=\widehat{KBA}=\frac{\widehat{CBA}}{2}$.

Mà ABCD là hình thang cân nên $\widehat{DAB}=\widehat{CBA}$ (tính chất hình thang cân).

Do đó $\widehat{KAB}=\widehat{KBA}$, suy ra ∆ABK là tam giác cân tại K.

b) Vì ∆ABK là tam giác cân nên KM là đường cao và cũng là đường trung tuyến ứng với cạnh đáy AB.

Do vậy M là trung điểm của AB nên AM = BM.

Bài 3. Cho tam giác cân EFG có EF = EG. Trên các cạnh EF và EG, lần lượt lấy các điểm H và I sao cho EH = EI.

a) Chứng minh HIGF là hình thang.

b) Chứng minh HIGF là hình thang cân.

Hướng dẫn giải

a) Ta có EH = EI nên ∆EHI là tam giác cân tại E.

Suy ra $\widehat{EHI}=\widehat{EIH}=\frac{180°-\hat{E}}{2}$ (1)

Lại có EF = EG nên ∆EFG là tam giác cân tại E.

Suy ra $\widehat{EFG}=\widehat{EGF}=\frac{180°-\hat{E}}{2}$ (2)

Từ (1) và (2) suy ra $\widehat{EHI}=\widehat{EFG}$.

Mà $\widehat{EHI}$ và $\widehat{EFG}$ ở vị trí đồng vị nên HI // FG (dấu hiệu nhận biết).

Suy ra tứ giác HIGF là hình thang.

b) Vì ∆EFG là tam giác cân nên $\hat{F}=\hat{G}$.

Suy ra hình thang HIGF là hình thang cân.

Bài 4. Cho hình thang ABCD (AD // BC) có AC = BD.

a) Hình thang ABCD là hình thang gì? Vì sao?

b) Chứng minh $\widehat{ADB}=\widehat{DAC}$ .

Hướng dẫn giải

a) Vì hai đường chéo của hình thang ABCD là AC và BD bằng nhau nên hình thang ABCD là hình thang cân.

b) Theo tính chất hình thang cân, ta có: AB = DC

Xét ∆ABD và ∆DCA có:

AD là cạnh chung;

AB = DC;

BD = AC.

Suy ra ∆ABD = ∆DCA (c.c.c)

Do đó $\widehat{ADB}=\widehat{DAC}$ (hai cạnh tương ứng).

Bài 5. Cho hình thang cân ABCD (như hình vẽ) có $\widehat{\text{BAD}}=60°.$  Số đo của $\widehat{\text{BCD}}$  bằng bao nhiêu?

Hướng dẫn giải

Vì ABCD là hình thang cân nên ta có: $\widehat{\text{A}}\text{ = }\widehat{\text{B}}$  và $\widehat{\text{C}}\text{ = }\widehat{\text{D}}$ .

Mà $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ . Suy ra $2\widehat{A}+2\widehat{C}=360°$ .

Nên $2\widehat{C}=360°-2\widehat{A}=360°-2.60°=240°.$  Suy ra $\widehat{C}=120°.$

Vậy $\widehat{C}=120°.$

Bài 6. Cho hình thang cân ABCD đáy nhỏ AB = 4 cm, đáy lớn CD = 10 cm, cạnh bên BC = 5 cm. Tính đường cao AH.

Hướng dẫn giải

Kẻ BI ⊥ CD tại I.

Vì ABCD là hình thang cân nên ta có:

 $\widehat{\text{D}}=\widehat{\text{C}}$

AD = BC

Do đó ΔAHD = ΔBKC (cạnh huyền – góc nhọn)

Suy ra DH = CK.

Hay $DH=\frac{1}{2}(CD-AB)=\frac{1}{2}(10-4)=3\text{ (}cm).$

Do ABCD là hình thang cân nên AD = BC = 5 cm.

Áp dụng định lý Pythagore vào tam giác ADH vuông tại H, ta có:

AD² = AH² + DH²

Suy ra AH² = AD² – DH² = 5² – 3² = 16.

Do đó AH = 4 cm.

Bài 7. Hình thang ABCD (AB // CD) trong hình bên dưới có phải hình thang cân không? Vì sao?

Hướng dẫn giải

Giả sử ABCD (AB // CD) là hình thang cân.

Khi đó, ta có: $\hat{A}=\hat{B}=140°,\hat{C}=\hat{D}=60°$.

Tổng 4 góc trong hình thang ABCD là $\hat{A}+\hat{B}+\hat{C}+\hat{D}=400°>360°$ .

Suy ra ABCD không phải là hình thang cân.

Bài 8. Cho hình thang MNPQ (MN // PQ) có $\widehat{NMP}=\widehat{MNQ},$  E là giao điểm của MP và NQ. Chứng minh hình thang MNPQ là hình thang cân.

Hướng dẫn giải

Vì MN // QP nên $\widehat{NMP}=\widehat{MPQ}$  và $\widehat{NQP}=\widehat{MNQ}$(các cặp góc so le trong)

Mà $\widehat{NMP}=\widehat{MNQ}\Rightarrow \widehat{NMP}=\widehat{MPQ}=\widehat{NQP}=\widehat{MNQ}$.

$\Delta MNE$ có $\widehat{NMP}=\widehat{MNQ}$ nên $\Delta MNE$cân tại E

Suy ra ME = NE (1)

$\Delta QEP$ có $\widehat{MPQ}=\widehat{NQP}$  nên $\Delta QEP$  cân tại E

Suy ra EQ = EP (2)

Từ (1) và (2) ta có: ME + EP = NE +  EQ hay MP = NQ

Suy ra MNPQ là hình thang cân (dấu hiệu nhận biết).

Bài 9. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Hướng dẫn giải

Vì ABCD (AB // CD) là hình thang cân nên $\hat{D}=\hat{C}$ và AD = BC.

Xét $\Delta AED$  và $\Delta BFC$  có: 

$\widehat{AED}=\widehat{BFC}=90°(AE\perp DC,BF\perp DC)$

$\hat{D}=\hat{C}$(chứng minh trên)

AD = BC (chứng minh trên)

Do đó $\Delta AED=\Delta BFC$  (cạnh huyền - góc nhọn)

Suy ra DE = CF (cạnh tương ứng bằng nhau).

2, Bài tập tự luyện

Bài 1: Cho hình thang ABCD có AB // CD, 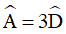 . Tính các góc của hình thang.

Bài 2: Cho hình thang ABCD (AB // CD), có AH và BK là hai đường cao của hình thang.

a) Chứng minh: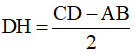

b) Biết AB = 6cm, CD = 14cm, AD = 5cm. Tính DH, AH và diện tích hình thang ABCD.

Bài 3: Cho hình thang ABCD (AB // CD) có CD = AD + BC. Gọi K là điểm thuộc đáy CD sao cho KD = AD. Chứng minh:

a) AK là tia phân giác góc A.

b) KC = BC.

Bài 4: Cho tam giác ABC vuông cân tại A có AB = 4cm. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tính diện tích tứ giác ABCD.

Bài 5: Cho hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc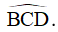 

Bài 6: Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai đáy AB và CD. Chứng minh EF vuông góc với AB.

Bài 7: Cho hình thang ABCD vuông tại A và D. Có AB = AD = 3cm, CD = 6cm. Tính số đo góc B, góc C.

Bài 8: Cho hình thang ABCD (AB // CD), Hai đường phân giác của góc C và góc D cắt nhau tại I thuộc đáy AB. Chứng minh rằng tổng độ dài hai cạnh bên bằng độ dài AB của hình thang.

Bài 9: Cho hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng AC là tia phân giác của góc C.

Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng qua M song song với CA cắt AB tại I. 

a) Tứ giác ACMI là hình gì?

b) AB + AC < AH + BC.

2. Bài tập bổ sung

Bài 1. Cho hình bình hành ABCD có BC = 2AB và số đo góc tại đỉnh A của hình bình hành là 60°. Gọi M, N theo thứ tự là trung điểm của BC và AD . Trên tia AB lấy điểm I sao cho B là trung điểm của AI. Chứng minh tứ giác ABMN là hình thang.

Bài 2. Cho tam giác ABC với ba trung tuyến AE, BD, CF đồng quy tại G. M và N lần lượt là trung điểm của GC và GB. Tứ giác MNDF là hình gì?

Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB, F ∈ AC); O là giao điểm của AH và EF. Chứng minh tứ giác EFCD là hình thang.

Bài 4. Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Lấy một điểm E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF. Chứng minh tứ giác OEFC là hình thang.

Bài 5. Cho tam giác ABC vuông tại A (AB < AC), D là trung điểm của BC. Lấy điểm E và F trên AB, AC sao cho DE ⊥ AB và DF ⊥ AC. Chứng minh tứ giác BDFE là hình thang.