Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Hỗn số là gì? Cách chuyển hỗn số thành phân số; Các phép tính với hỗn số, tài liệu gồm đầy đủ về lý thuyết Hỗn số, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Hỗn số là gì? Cách chuyển hỗn số thành phân số; Các phép tính với hỗn số

A. Lý thuyết Hỗ số

1. Khái niệm Hỗn số

+ Khái niệm: Hỗn số gồm hai thành phần là phần nguyên và phần phân số.

Ví dụ: Cho hỗn số $3\frac{7}{12}$

Phần nguyên của hỗn số là 3 và phần phân số là $\frac{7}{12}$.

Nhận xét:

– Giá trị của hỗn số bao giờ cũng lớn hơn 1.

– Phần phân số của hỗn số bao giờ cũng bé hơn 1.

2. Cách đọc hỗn số

- Bước 1: đọc phần nguyên

- Bước 2: đọc “và”

- Bước 3: đọc phần phân số

Ví dụ: Hỗn số $3\frac{7}{12}$ được đọc là “ba và bảy phần mười hai”.

3. Cách chuyển hỗn số thành phân số

+ Để chuyển một hỗn số thành phân số, ta thực hiện các bước sau:

- Bước 1: Lấy phần nguyên nhân với mẫu số, kết quả nhận được đem cộng với tử số

- Bước 2: Thay kết quả ở bước 1 thành tử số mới, giữ nguyên mẫu số. Ta được một phân số mới được chuyển từ hỗn số đã cho

Ví dụ: Chuyển các hỗn số thành phân số: $2\frac{1}{6};5\frac{3}{4};2\frac{2}{9}$

Lời giải:

$$\begin{gathered} 2\frac{1}{6}=\frac{2\times 6+1}{6}=\frac{13}{6} \\ 5\frac{3}{4}=\frac{5\times 4+3}{4}=\frac{23}{4} \\ 2\frac{2}{9}=\frac{2\times 9+2}{9}=\frac{20}{9} \end{gathered}$$

4. Cách chuyển phân số thành hỗn số

+ Để chuyển một phân số sang hỗn số, ta thực hiện theo các bước sau:

- Bước 1: Lấy tử số chia cho mẫu số

- Bước 2: Phần nguyên là số nguyên trong hỗn số

- Bước 3: Phần dư là tử số mới trong hỗn số

- Bước 4: Phần mẫu số giữ nguyên giá trị

Ví dụ: Chuyển các phân số thành hỗn số: $\frac{9}{2};\frac{16}{3};\frac{27}{5}$

Lời giải:

Ta có:

9 : 2 = 4 (dư 1); 16 : 3 = 5 (dư 1) và 27 : 5 = 5 (dư 2)

Vậy các phân số đã cho được viết dưới dạng hỗn số là:

$$\begin{gathered} \frac{9}{2}=4\frac{1}{2} \\ \frac{16}{3}=5\frac{1}{3} \\ \frac{27}{5}=5\frac{2}{5} \end{gathered}$$

* Chú ý: Bất kỳ phân số nào có tử số lớn hơn mẫu số đều có thể đổi thành hỗn số và ngược lại. Tuy nhiên nếu tử số bằng hoặc nhỏ hơn mẫu số thì không thể thực hiện được việc chuyển phân số thành hỗn số.

5. Phép cộng và phép trừ hỗn số

* Để thực hiện phép cộng và phép trừ hỗn số, ta có hai cách làm sau:

Cách 1: Chuyển hỗn số về phân số

+ Muốn cộng (hoặc trừ) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi cộng (hoặc) trừ hai phân số vừa chuyển đổi.

Ví dụ: Thực hiện phép tính:

a) $4\frac{1}{5}+1\frac{6}{15}$

b) $5\frac{1}{2}-3\frac{1}{4}$

Lời giải:

a) $4\frac{1}{5}+1\frac{6}{15}$

$$\begin{gathered} =\frac{21}{5}+\frac{21}{15} \\ =\frac{63}{15}+\frac{21}{15}=\frac{84}{15} \end{gathered}$$

b) $5\frac{1}{2}-3\frac{1}{4}$

$$\begin{gathered} =\frac{11}{2}-\frac{13}{4} \\ =\frac{22}{4}-\frac{13}{4}=\frac{9}{4} \end{gathered}$$

Cách 2: Tách hỗn số thành phần nguyên và phần phân số, sau đó thực hiện phép cộng (trừ) phần nguyên và phép cộng (trừ) phần phân số.

Ví dụ: Thực hiện phép tính:

a) $1\frac{1}{6}+2\frac{7}{12}$

b) $5\frac{3}{4}-2\frac{1}{8}$

Lời giải:

a) $1\frac{1}{6}+2\frac{7}{12}$

$$\begin{gathered} =\left(1+2\right)+\left(\frac{1}{6}+\frac{7}{12}\right) \\ =3+\frac{9}{12}=3+\frac{3}{4}=3\frac{3}{4} \end{gathered}$$

b) $5\frac{3}{4}-2\frac{1}{8}$

$$\begin{gathered} =\left(5-2\right)+\left(\frac{3}{4}-\frac{1}{8}\right) \\ =3+\frac{5}{8}=3\frac{5}{8} \end{gathered}$$

6. Phép nhân và phép chia hỗn số

+ Để thực hiện nhân (hoặc chia) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi nhân (hoặc chia) hai phân số vừa chuyển đổi.

Ví dụ: Thực hiện phép tính:

a) $4\frac{7}{8}\times 1\frac{3}{13}$

b) $4\frac{2}{5}:1\frac{7}{15}$

Lời giải:

a) $4\frac{7}{8}\times 1\frac{3}{13}$

$$\begin{gathered} =\frac{39}{8}\times \frac{16}{13}=\frac{39\times 16}{8\times 13} \\ =\frac{3\times 2}{1\times 1}=6 \end{gathered}$$

b) $4\frac{2}{5}:1\frac{7}{15}$

$$\begin{gathered} =\frac{22}{5}:\frac{22}{15} \\ =\frac{22}{5}\times \frac{15}{22}=3 \end{gathered}$$

7. So sánh hỗn số

* Để thực hiện so sánh hỗn số, ta có hai cách dưới đây:

Cách 1: Chuyển hỗn số về phân số: để so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.

Ví dụ: So sánh hai hỗn số: $5\frac{1}{4}$ và $2\frac{2}{3}$

Lời giải:

Ta có: $5\frac{1}{4}=\frac{21}{4}$ và $2\frac{2}{3}=\frac{8}{3}$

Quy đồng mẫu số hai phân số, ta có:

$$\begin{gathered} \frac{21}{4}=\frac{21\times 3}{4\times 3}=\frac{63}{12} \\ \frac{8}{3}=\frac{8\times 4}{3\times 4}=\frac{32}{12} \end{gathered}$$

Vì $\frac{63}{12}>\frac{32}{12}$ nên $5\frac{1}{4}>2\frac{2}{3}$

Cách 2: So sánh phần nguyên và phần phân số. Khi so sánh hai hỗn số:

- Hỗn số nào có phần nguyên lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần nguyên nhỏ hơn thì hỗn số đó nhỏ hơn

- Nếu hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì hỗn số đó lớn hơn.

Ví dụ: So sánh các hỗn số sau:

a) $2\frac{1}{4}$ và $3\frac{5}{6}$

b) $4\frac{5}{12}$ và $4\frac{5}{8}$

Lời giải:

a) $2\frac{1}{4}$ và $3\frac{5}{6}$

Hỗn số $2\frac{1}{4}$ có phần nguyên bằng 2 và hỗn số $3\frac{5}{6}$ có phần nguyên bằng 3

Vì 2 < 3 nên $2\frac{1}{4}<3\frac{5}{6}$.

b) $4\frac{5}{12}$ và $4\frac{5}{8}$

Hai hỗn số có cùng phần nguyên nên ta so sánh phần phân số của hai hỗn số

Vì $\frac{5}{12}<\frac{5}{8}$ nên $4\frac{5}{12}<4\frac{5}{8}$

B. Bài tập vận dụng về Hỗn số

1. Bài tập trắc nghiệm

Câu 1: Cho hình vẽ như sau:

Hỗn số thích hợp cho đối với hình vẽ đã cho là:

A. $1\frac{1}{2}$

B. $2\frac{1}{2}$

C. $2\frac{1}{3}$

D. $1\frac{1}{3}$

Câu 2:  Hỗn số $1\frac{3}{4}$ được đọc là:

A. Ba một phần tư

B. Bốn một phần ba

C. Một ba phần tư

D. Hai ba phần tư

Câu 3:  Phần nguyên của hỗn số $5\frac{4}{9}$ là:

A. 5

B.  4

C.  9

D. 3

Câu 4: Phần phân số của hỗn số $4\frac{7}{15}$ là

A. $\frac{4}{15}$

B. $\frac{15}{7}$

C. $\frac{15}{4}$

D. $\frac{7}{15}$

Câu 5:  Hỗn số $6\frac{2}{5}$ được viết dưới dạng phân số là:

A. $\frac{5}{32}$

B. $\frac{17}{5}$

C. $\frac{32}{5}$

D. $\frac{16}{5}$

Câu 6: Khi chuyển phân số $\frac{58}{9}$ thành hỗn số ta được hỗn số có phần nguyên là:

A. $6\frac{4}{9}$

B. $5\frac{13}{9}$

C. $6\frac{7}{9}$

D. $5\frac{4}{9}$

Câu 7: Điền dấu thích hợp vào chỗ chấm: $3\frac{4}{5}\cdot \cdot \cdot 3\frac{5}{6}$

A. <

B. >

C. =

D. Không so sánh được  

Câu 8: Cho các phép tính :

$$\begin{gathered} \mathrm{a})2\frac{1}{7}+3\frac{5}{7}=\frac{...}{7} \\ \mathrm{b})5\frac{2}{15}-1\frac{8}{15}=\frac{...}{15} \end{gathered}$$

Các số được điền vào các chỗ trống lần lượt là:

A. 34, 18

B. 34, 54

C. 54, 34

D. 18, 34

Câu 9: Phân số thích hợp chỉ phần tô đậm của hình sau là:

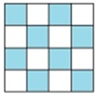
A. $\frac{3}{2}$

B. $\frac{6}{16}$

C. $\frac{1}{2}$

D. $\frac{9}{16}$

Câu 10: Viết thương $47:28$dưới dạng phân số ta được:

A. $\frac{47}{10}$và $\frac{28}{10}$

B. $\frac{47}{28}$

C. $\frac{28}{47}$

D. $1\frac{47}{28}$

Câu 11: Rút gọn phân số sau: $\frac{21}{30}$

A. $\frac{7}{6}$

B. $\frac{3}{5}$

C. Không rút gọn được

D. $\frac{7}{10}$

Câu 12: Trong các phân số sau, phân số nào là phân số thập phân:

$\frac{10}{7};\frac{4}{10};\frac{100}{51};\frac{65}{1000};\frac{4}{3000}$

A. $\frac{10}{7};\frac{100}{51}$

B. $\frac{4}{10}$

C. $\frac{65}{1000};\frac{4}{3000}$

D. $\frac{4}{10};\frac{65}{1000}$

Câu 13: Chuyển phân số sau thành phân số thập phân: $\frac{11}{25}=\dots$

A. $\frac{44}{10}$

B. $\frac{11}{10}$

C. $\frac{11}{1000}$

D. $\frac{44}{100}$

Câu 14: Hỗn số thích hợp biểu diễn số phần hình tròn được tô màu điền vào chỗ chấm là :

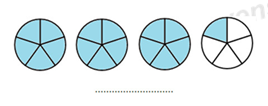
A. $2\frac{6}{12}$

B. $3\frac{1}{5}$

C. $4\frac{1}{5}$

D. $3\frac{2}{5}$

Câu 15: Tính: $3\frac{1}{2}+2\frac{2}{5}=\dots$

A. $\frac{37}{10}$

B. $\frac{52}{5}$

C. $\frac{59}{10}$

D. $\frac{42}{5}$

Câu 16: Mẹ làm 20 chiếc bánh rán rất ngon, trong đó có $\frac{2}{5}$số bánh rán là bánh ngọt, $\frac{1}{4}$số bánh rán là bánh mặn, số bánh rán còn lại là bánh vừng. Hỏi mẹ đã làm bao nhiêu chiếc bánh vừng?

A. 7

B. 8

C. 6

D. 10

2. Bài tập tự luận

Câu 1: Chuyển các hỗn số sau thành phân số:

$$\begin{gathered} \mathrm{a}\left)1\frac{2}{7} \\ \mathrm{b}\right)3\frac{2}{5} \\ \mathrm{c}\left)6\frac{7}{8} \\ \mathrm{d}\right)3\frac{8}{17} \\ \mathrm{e}\left)11\frac{4}{15} \\ \mathrm{f}\right)16\frac{10}{21} \end{gathered}$$        

Câu 2: Chuyển các phân số sau thành hỗn số:

$$\begin{gathered} \mathrm{a}\left)\frac{11}{4} \\ \mathrm{b}\right)\frac{41}{6} \\ \mathrm{c}\left)\frac{77}{9} \\ \mathrm{d}\right)\frac{82}{5} \\ \mathrm{e}\left)\frac{123}{14} \\ \mathrm{f}\right)\frac{235}{24} \end{gathered}$$

Câu 3: So sánh các hỗn số sau:

a) $2\frac{9}{10}$ và $5\frac{1}{10}$

b) $7\frac{1}{2}$ và $4\frac{3}{5}$

c) $3\frac{3}{7}$ và $3\frac{2}{5}$

d) $5\frac{6}{9}$ và $5\frac{2}{3}$

Câu 4: Chuyển các hỗn số sau thành phân số rồi thực hiện các phép tính sau:

$$\begin{gathered} \mathrm{a})4\frac{1}{7}+1\frac{3}{7} \\ \mathrm{b})5\frac{3}{8}+2\frac{1}{4} \\ \mathrm{c})7\frac{1}{5}-3\frac{1}{2} \\ \mathrm{d})3\frac{2}{11}\times 2\frac{3}{7} \\ \mathrm{e})2\frac{5}{6}:3\frac{9}{11} \\ \mathrm{f})4\frac{7}{12}:3\frac{3}{4} \end{gathered}$$

Câu 5: Một cửa hàng có $72\frac{3}{4}$ kg gạo. Cửa hàng đã bán được $\frac{2}{3}$  số gạo đó, sau đó cửa hàng nhập thêm số gạo gấp 3 lần số gạo còn lại. Hỏi sau khi nhập thêm cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?

Câu 6: Chuyển các phân số sau thành hỗn số rồi thực hiện phép tính:

a,	b,	c,
d,	e,	f,

Câu 7: Chuyển các phân số sau thành hỗn số (theo mẫu)

Mẫu:  Có = 2 (dư 3). Vậy 

a,

b,

c,

d,

e,

Câu 8: Chuyển hỗn số thành phân số rồi thực hiện phép tính:

a) $3\frac{1}{2}+2\frac{2}{5}=\dots$

b) $5\frac{3}{8}-1\frac{2}{3}=\dots$

c) $6\frac{3}{4}\times 3\frac{7}{13}=\dots$

d) $9\frac{5}{6}:8\frac{1}{7}=\dots$

Câu 9. Tính:

$$\begin{gathered} \frac{1}{3}+\frac{1}{4}=\dots \\ \frac{6}{5}-\frac{6}{10}=\dots \\ \frac{2}{5}\times \frac{3}{8}=\dots \\ \frac{9}{11}:\frac{21}{15}=\dots \end{gathered}$$

Câu 10. Tính:

$$\begin{gathered} \frac{5}{11}:\frac{5}{3}+\frac{7}{55}=\dots \\ 7-\frac{5}{6}\times 5=\dots \end{gathered}$$

Câu 11: Phương, Hòa, Dương cùng hái dâu tây. Phương hái được 1 hộp và $\frac{1}{2}$hộp, Hòa hái được 1 hộp và $\frac{3}{4}$hộp, Dương hái được 1 hộp và $\frac{3}{4}$hộp.

a) Viết hỗn số biểu diễn số hộp dâu tây mà mỗi bạn hái được:

b) Tính số hộp dâu tây cả ba bạn hái được:

c) Nếu đem tất cả số dâu tây hái được chia đều cho 3 bạn thì mỗi bạn được mấy phần hộp dâu tây?

Câu 12. Chuyển hỗn số thành phân số rồi thực hiện phép tính:

a) $3\frac{1}{2}+2\frac{2}{5}=\dots$

b) $5\frac{3}{8}-1\frac{2}{3}=\dots$

c) $6\frac{3}{4}\times 3\frac{7}{13}=\dots$

d) $9\frac{5}{6}:8\frac{1}{7}=\dots$

Câu 13. So sánh các hỗn số:

a) $7\frac{3}{7}\dots 6\frac{3}{7}$

b) $3\frac{2}{3}\dots 3\frac{4}{5}$

c) $7\frac{5}{6}\dots 8\frac{5}{6}$

d) $7\frac{4}{12}\dots 7\frac{1}{3}$

C. Bài tập tự luyện

Bài 1. Hỗn số gồm bao nhiêu thành phần?

A. Một thành phần, đó là phần nguyên

B. Một thành phần, đó là phần phân số

C. Hai thành phần, đó là phần nguyên và phần phân số.

D. Hai thành phần, đó là phần nguyên và phần số thập phân.

Bài 2. Chọn hỗn số trong các đáp án sau:

A. 5    

B. $\frac{27}{100}$   

C. $\frac{100}{27}$   

D. $5\frac{27}{100}$

Bài 3. Viết hỗn số thích hợp với mỗi hình vẽ sau:

Bài 4. a) Đọc rồi nêu phần nguyên, phần phân số của mỗi của mỗi hỗn số sau:

$5\frac{15}{1000};21\frac{9}{100};8\frac{1005}{100000}$

b) Viết các hỗn số sau.

● Ba và hai mươi sáu phần mười

● Chín mươi hai và năm mươi tư phần một trăm nghìn

● Mười một và một trăm linh một phần một chục nghìn

Bài 5. Viết các phân số thập phân ở dạng hỗn số: $\frac{62}{10}$; $\frac{3050}{1000}$; $\frac{827}{10}$

Bài 6. Chuyển các hỗn số sau thành phân số: $6\frac{5}{10};3\frac{24}{1000};2\frac{42001}{100000}$

Bài 7. Viết các số đo sau dưới dạng hỗn số:

a) 4812 m = …………….. km	b) 642 cm = …………... m
c) 12 m 9 dm = …………. m	d) 5 km 9 m = ……….... km

Bài 8. Điền dấu >; <; = thích hợp vào chỗ trống

$2\frac{5}{10}\mathrm{......}3\frac{5}{10}$	$6\frac{23}{100}\mathrm{.....}6\frac{32}{100}$
$\frac{425}{100}\mathrm{......}4\frac{25}{100}$	$\frac{30005}{10000}\mathrm{......}3\frac{5}{10000}$

Bài 9. Đúng ghi Đ, sai ghi S

$8\frac{56}{100}=56+\frac{8}{100}$	$3\frac{8}{10}=\frac{3\times 10+8}{10}=\frac{38}{10}$
$9\frac{3}{1000}=\frac{3\times 1000+9}{1000}=\frac{3009}{1000}$	$\frac{68}{20}=\frac{34}{10}=3\frac{4}{10}$

Bài 10. Chọn đáp án sai.

Cô Nga có 12 túi kẹo, mỗi túi có 10 viên kẹo. Cô chia đều số kẹo đó cho 10 bạn. Vậy mỗi bạn nhận được:

A.$1\frac{2}{10}$túi kẹo   

B. 12 viên kẹo    

C. $\frac{12}{10}$túi kẹo   

D. $\frac{12}{10}$viên kẹo