Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Trọng tâm của tứ diện: Định nghĩa, các dạng bài tập về trọng tâm tứ diện, tài liệu gồm đầy đủ về lý thuyết Trọng tâm của tứ diện, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Trọng tâm của tứ diện: Định nghĩa, các dạng bài tập về trọng tâm tứ diện

A. Lý thuyết

1. Định nghĩa

G là trọng tâm tứ diện thì G là trung điểm của đoạn nối trung điểm hai cạnh đối của tứ diện.

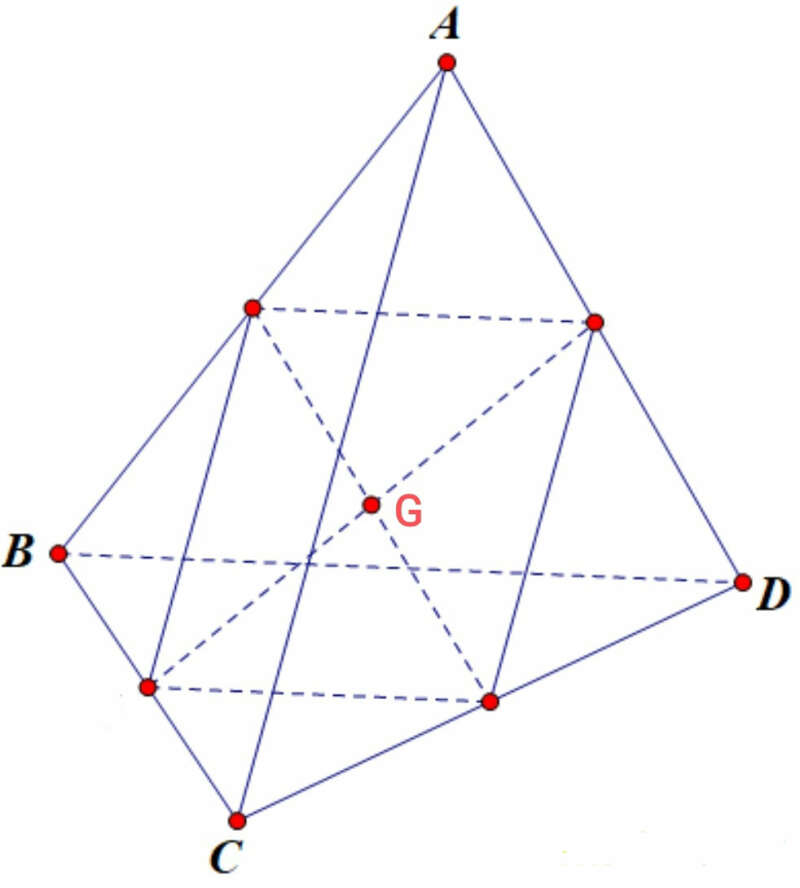
2. Tính chất của trọng tâm tứ diện

Một số tính chất của trọng tâm tứ diện ABCD, với G là trọng tâm của tứ diện:

- Tính chất cơ bản: Tổng vector từ trọng tâm G đến mỗi đỉnh A, B, C, D của tứ diện là vector không: GA  + GB + GC + GD = 0. Điều này có nghĩa là tổng các vector từ trọng tâm G đến các đỉnh của tứ diện bằng vector không, tức là vector hợp của các vector đó cùng hướng và cùng độ dài.

- Tính chất liên quan đến trung điểm cạnh: Trọng tâm G là trung điểm của đoạn nối 2 trung điểm của hai cạnh đối nhau bất kì trong tứ diện. Điều này có nghĩa là nếu E và F lần lượt là trung điểm của các cạnh AB và CD (hoặc BC và AD, AC và BD), thì trọng tâm G là trung điểm của đoạn EF.

- Tính chất liên quan đến đỉnh và trọng tâm tam giác đáy:

+ Trọng tâm G nằm trên đường nối một đỉnh của tứ diện với trọng tâm của tam giác đáy tương ứng. Nghĩa là nếu H là trọng tâm của tam giác đáy ABC (hoặc BCD, CDA, DAB), thì đường thẳng GH là đường thẳng nối từ đỉnh không nằm trên tam giác đáy đến trọng tâm của tam giác đáy đó.

+ Khoảng cách từ trọng tâm G đến đỉnh của tứ diện bằng ba lần khoảng cách từ G đến trọng tâm của tam giác đáy tương ứng. Nghĩa là nếu H là trọng tâm của tam giác đáy ABC (hoặc BCD, CDA, DAB), thì khoảng cách GH bằng ba lần khoảng cách GH.

=> Tất cả những tính chất trên đều đúng với trọng tâm của tứ diện ABCD. Các tính chất này được sử dụng rộng rãi trong các bài toán hình học và tính toán liên quan đến tứ diện, giúp xác định vị trí và tính chất của trọng tâm trong không gian.

3. Cách xác định trọng tâm tứ diện

Để vẽ trọng tâm của tứ diện ABCD, chúng ta có hai cách sau:

Cách 1: Sử dụng trung điểm của các cặp cạnh chéo

- Cho tứ diện ABCD, ta cần xác định trọng tâm của nó.

- Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

- Theo định nghĩa trọng tâm, trọng tâm của tứ diện là điểm giao của ba đường thẳng nối trung điểm của các cặp cạnh chéo. Do đó, ta cần nối đường thẳng MP, NQ và NR.

- Khi đó, ba đường thẳng MP, NQ và NR đồng quy tại một điểm duy nhất. Điểm đó chính là trọng tâm của tứ diện ABCD.

Cách 2: Sử dụng trọng tâm của tam giác đáy và một đoạn thẳng có tỷ lệ

- Cho tứ diện ABCD, ta có tam giác BCD.

- Trọng tâm G của tam giác BCD là trung điểm của các đỉnh B, C và D.

- Để xác định trọng tâm của tứ diện ABCD, ta sử dụng một đoạn thẳng AG, với A là một đỉnh của tứ diện và G là trọng tâm của tam giác BCD.

- Lấy điểm K trên đoạn thẳng AG sao cho AK = 3 x GK. Điểm K chính là trọng tâm của tứ diện ABCD.

Cả hai cách trên đều dẫn đến việc xác định trọng tâm của tứ diện ABCD. Trọng tâm là một điểm quan trọng trong tứ diện, nó có tọa độ trung bình của các đỉnh và được sử dụng trong các tính toán và phân tích hình học của tứ diện. Việc biết vị trí trọng tâm giúp ta hiểu về sự phân bố khối lượng của tứ diện và tương tác với các lực hoặc điểm cân bằng của nó.

4. Các bài tập liên quan trọng tâm của tứ diện

- Bài tập tính trọng tâm: Cho các tọa độ của các đỉnh A, B, C, D của tứ diện ABCD, hãy tính tọa độ của trọng tâm G của tứ diện ABCD.

- Bài tập chứng minh trọng tâm: Cho các đỉnh A, B, C, D của tứ diện ABCD và biết G là trọng tâm của tứ diện này. Hãy chứng minh rằng G cũng là trọng tâm của tứ diện A’B’C’D’ nếu ta dịch chuyển tứ diện ABCD theo một vector bất kỳ.

- Bài tập tính độ dài đoạn thẳng: Cho trọng tâm G của tứ diện ABCD và một trong các đỉnh A của tứ diện. Hãy tính độ dài đoạn thẳng AG.

- Bài tập tính khoảng cách: Cho tọa độ các đỉnh A, B, C, D của tứ diện ABCD. Hãy tính khoảng cách từ trọng tâm G của tứ diện đến một trong các đỉnh A, B, C, D.

- Bài tập tính thể tích: Cho tọa độ các đỉnh A, B, C, D của tứ diện ABCD. Hãy tính thể tích của tứ diện ABCD bằng cách sử dụng trọng tâm G và các đỉnh A, B, C, D.

- Bài tập tính diện tích: Cho tọa độ các đỉnh A, B, C, D của tứ diện ABCD. Hãy tính diện tích mặt phẳng ABC bằng cách sử dụng trọng tâm G và các đỉnh A, B, C.

- Bài tập chứng minh trọng tâm thuộc đoạn thẳng: Cho tứ diện ABCD và trọng tâm G của nó. Hãy chứng minh rằng trọng tâm G thuộc đoạn thẳng nối trung điểm của hai đoạn thẳng AB và CD.

B. Bài tập về Trọng tâm của tứ diện

Bài 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn $\overrightarrow{AI}=3\overrightarrow{IG}$, ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

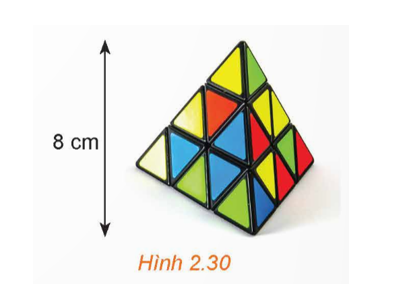
Phương pháp giải

Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để tính: Trong không gian, tích của một số thực $k\ne 0$ với một vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ là một vectơ, kí hiệu là $k\overrightarrow{a}$ được xác định như sau:

- Cùng hướng với vectơ $\overrightarrow{a}$ nếu $k>0$, ngược hướng với vectơ $\overrightarrow{a}$ nếu $k<0$.

- Có độ dài bằng $\left|k\right|\left|\overrightarrow{a}\right|$.

Lời giải:

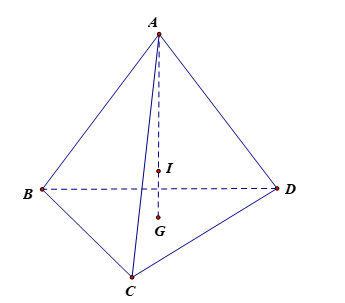
Giả sử khối rubik (đồng chất) hình tứ diện đều được mô phỏng như hình vẽ.

G là trọng tâm DBCD, I là trọng tâm của tứ diện

Vì ABCD là hình tứ diện đều nên AG ^ (BCD) và AG = 8 cm.

Vì $\overrightarrow{AI}=3\overrightarrow{IG}$ nên 3 điểm A, I, G thẳng hàng và $IG=\frac{1}{4}AG$.

Do đó IG ^ (BCD). Khi đó $d\left(I,\left(BCD\right)\right)=IG=\frac{1}{4}AG=2$ cm.

Bài 2: Gọi $G$ là trọng tâm tứ diện $ABCD$. Gọi $A^{\prime }$ là trọng tâm của tam giác $BCD$. Tính tỉ số $\frac{GA}{G{A}^{\prime }}$.

A. 2

B. 3

C. $\frac{1}{3}$

D. $\frac{1}{2}$

Lời giải:

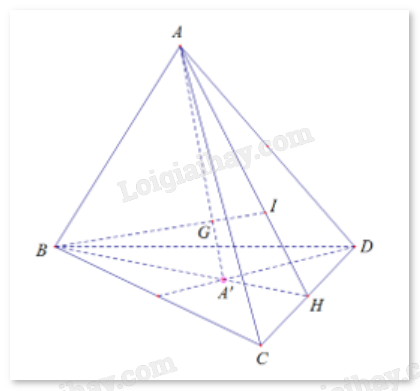
Gọi I là trọng tâm tam giác ACD

H là trung điểm CD

Nối BI cắt AA’, ta được trọng tâm G của tứ diện

Xét mặt phẳng (ABH) có:

$\frac{IH}{AH}=\frac{A^{\prime }H}{BH}=\frac{1}{3}$ (vì A’ và I lần lượt là trọng tâm các tam giác BCD và ACD).

Suy ra A’I//AB (định lý Thales đảo).

Khi đó $\frac{A^{\prime }I}{AB}=\frac{IH}{AH}=\frac{A^{\prime }H}{BH}=\frac{1}{3}$ (hệ quả định lý Thales).

A’I//AB cũng cho thấy $\frac{A^{\prime }I}{AB}=\frac{G{A}^{\prime }}{GA}=\frac{IH}{AH}=\frac{1}{3}$ (hệ quả định lý Thales).

Vậy $\frac{GA}{G{A}^{\prime }}=3$.

Đáp án : B

Bài 3: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 2), B(-2; 1; 3), C(3; 2; 4), D(6; 9; -5). Hãy tìm tọa độ trọng tâm của tứ diện ABCD?

A. (2; 3; -1)

B. (2; -3; 1)

C. (2; 3; 1)

D. (-2; 3; 1)

Lời giải:

Đáp án là C.

Gọi G(x; y; z) là trọng tâm của tứ diện  ABCD

Toạ độ trọng tâm của tứ diện ABCD

=> Tọa độ G(2; 3; 1)

Bài 4: Gọi G là trọng tâm của tứ diện ABCD

a. Chứng minh rằng đường thẳng đi qua G và một đỉnh của tứ diện sẽ đi qua trọng tâm của mặt đối diện với đỉnh ấy

b. Gọi A’ là trọng tâm của mặt BCD. Chứng minh rằng GA = 3GA’

Phương pháp giải:

- G là trọng tâm tứ diện thì G là trung điểm của đoạn nối trung điểm hai cạnh đối của tứ diện.

- Định lí Menelaus: Giả sử đường thẳng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :

$\frac{MB}{MC}.\frac{NC}{NA}.\frac{PA}{PB}=1$

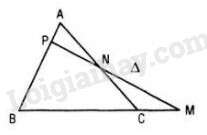
Lời giải:

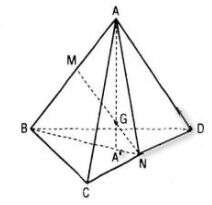
a. Gọi M, N là trung điểm của AB, CD.

G là trọng tâm tứ diện nên G là trung điểm của MN hay GM=GN.

Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD.

Ta chứng minh A' là trọng tâm tam giác BCD hay A’B = 2A’N.

Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ ta có :

$\frac{AM}{AB}.\frac{GN}{GM}.\frac{A^{\prime }B}{A^{\prime }N}=1$$\Rightarrow \frac{1}{2}.1.\frac{A^{\prime }B}{A^{\prime }N}=1\Rightarrow A^{\prime }B=2A^{\prime }N$

Vậy A’ là trọng tâm của ΔBCD

Tương tự BG ,CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC.

b. Chứng minh GA = 3GA’

Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN ta có :

$\frac{MA}{MB}.\frac{G{A}^{\prime }}{GA}.\frac{NB}{N{A}^{\prime }}=1$$\Rightarrow 1.\frac{G{A}^{\prime }}{GA}.3=1$

$\Rightarrow GA=3G{A}^{\prime }\left(dpcm\right)$ 

Bài 5: Tọa độ trọng tâm tứ diện ABCD là:

A. $G\left(\frac{x_A+x_B+x_C+x_D}{3};\frac{y_A+y_B+y_C+y_D}{3};\frac{z_A+z_B+z_C+z_D}{3}\right)$

B. $G\left(\frac{x_A+x_B+x_C+x_D}{4};\frac{y_A+y_B+y_C+y_D}{4};\frac{z_A+z_B+z_C+z_D}{4}\right)$

C. $G\left(\frac{x_A+x_B+x_C+x_D}{2};\frac{y_A+y_B+y_C+y_D}{2};\frac{z_A+z_B+z_C+z_D}{2}\right)$

D. $G\left(\frac{x_A+x_B-x_C+x_D}{4};\frac{y_A+y_B-y_C+y_D}{4};\frac{z_A+z_B-z_C+z_D}{4}\right)$

Lời giải:

Tọa độ trọng tâm tứ diện ABCD là

$G\left(\frac{x_A+x_B+x_C+x_D}{4};\frac{y_A+y_B+y_C+y_D}{4};\frac{z_A+z_B+z_C+z_D}{4}\right)$

Đáp án cần chọn là: B

Bài 6: Cho tứ diện ABCD có G là trọng tâm tứ diện. Khi hệ thức véc tơ $\overrightarrow{\mathrm{MG}}=\mathrm{k}.\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}\right)$ đúng với mọi điểm M thì giá trị của k là

A. $\mathrm{k}=\frac{1}{2}$

B. k = 1

C. $\mathrm{k}=\frac{1}{3}$

D. $\mathrm{k}=\frac{1}{4}$

Lời giải:

G là trọng tâm tứ diện ABCD $\iff$ $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}+\overrightarrow{\mathrm{GD}}=\overrightarrow{0}$

$\iff$$\left(\overrightarrow{\mathrm{GM}}+\overrightarrow{\mathrm{MA}}\right)+\left(\overrightarrow{\mathrm{GM}}+\overrightarrow{\mathrm{MB}}\right)$$+\left(\overrightarrow{\mathrm{GM}}+\overrightarrow{\mathrm{MC}}\right)+\left(\overrightarrow{\mathrm{GM}}+\overrightarrow{\mathrm{MD}}\right)=\overrightarrow{0}$, với mọi điểm M

$\iff$$\overrightarrow{\mathrm{MG}}=\frac{1}{4}.\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}\right)$, với mọi điểm M.

Vậy $\mathrm{k}=\frac{1}{4}$

Chọn đáp án D.

Bài 7: Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?

$A. \stackrel{\rightharpoonup }{GA} + \stackrel{\rightharpoonup }{GB} +\hspace{0.17em}\stackrel{\rightharpoonup }{GC} +\hspace{0.17em}\stackrel{\rightharpoonup }{GD} = 0$

$B. \stackrel{\rightharpoonup }{OG} = \frac{1}{4}(\stackrel{\rightharpoonup }{OA} + \stackrel{\rightharpoonup }{OB} +\hspace{0.17em}\stackrel{\rightharpoonup }{OC} +\hspace{0.17em}\stackrel{\rightharpoonup }{OD})$

$C. \stackrel{\rightharpoonup }{AG} = \frac{1}{4}(\stackrel{\rightharpoonup }{AB} + \stackrel{\rightharpoonup }{AC} +\hspace{0.17em}\stackrel{\rightharpoonup }{AD})$

$D. \stackrel{\rightharpoonup }{AG} = \frac{2}{3}(\stackrel{\rightharpoonup }{AB} + \stackrel{\rightharpoonup }{AC} +\hspace{0.17em}\stackrel{\rightharpoonup }{AD})$

Lời giải:

Đáp án A

G là trọng tâm tứ diện ABCD

Bài 8: Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi G1 là giao điểm của AG và mặt phẳng (BCD), G2 là giao điểm của BG và mặt phẳng (ACD). Khẳng định nào sau đây là đúng?

A. $G_1{G}_2//AB$

B. $G_1{G}_2//AC$

C. $G_1{G}_2//CD$

D. $G_1{G}_2//AD$ 

Lời giải: