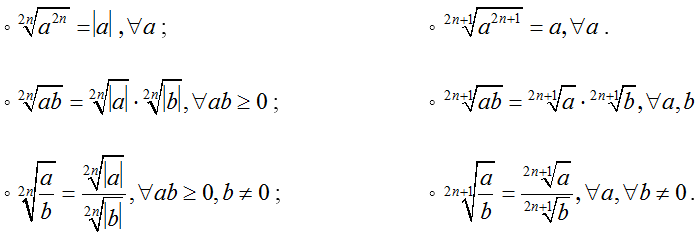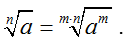Công thức lũy thừa đầy đủ, chi tiết và 20 bài tập ví dụ

Admin Vietjack Ngày: 13-11-2024 Tổng hợp kiến thức

Tải xuống 11 4.3 K 19

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ tài liệu Công thức lũy thừa đầy đủ, chi tiết và bài tập ví dụ, tài liệu tổng hợp lí thuyết cơ bản, tuyển chọn những câu hỏi trắc nghiệm có đáp án và lời giải chi tiết, giúp các em học sinh lớp 12 có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh có một kì ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Công thức lũy thừa đầy đủ, chi tiết và bài tập ví dụ

1. Lí thuyết Lũy thừa

a. Lũy thừa với số mũ nguyên

- Lũy thừa với số mũ nguyên dương

Cho $a \in ℝ$ , $n \in ℕ^{*}$ . Khi đó: $a^{n} = \underset{n s ô a}{\underset{⏟}{a . a ... a}}$

- Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0

Cho $a \neq 0$ . Khi đó: $a^{- n} = \frac{1}{a^{n}}; a^{0} = 1$

VD: $2^{- 3} = \frac{1}{2^{3}} = \frac{1}{8}$

- Chú ý: Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.

+ $0^{0}$ và $0^{- n}$ không có nghĩa.

b. Căn bậc n

- Cho số thực b và số nguyên dương $n \geq 2$ .

Số a được gọi là căn bậc n của số b nếu $a^{n} = b$

VD: 4 là căn bậc ba của 64 vì $4^{3} = 64$

- Khi n lẻ, $b \in ℝ$ : Tồn tại duy nhất $\sqrt[n]{b}$

Công thức lũy thừa đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

c. Lũy thừa với số mũ hữu tỉ

- Cho số thực $a > 0$ và số hữu tỉ $r = \frac{m}{n}$ , trong đó $m \in ℤ, n \geq 2$

Khi đó: $a^{r} = a^{\frac{m}{n}} = \sqrt[n]{a^{m}}$ . VD: $2^{\frac{1}{3}} = \sqrt[3]{2}$

d. Lũy thừa với số mũ vô tỉ

- Giả sử a là một số dương, $α$ là một số vô tỉ, $(r_{n})$ là một dãy số hữu tỉ sao cho $\lim_{n \to + \infty} r_{n} = α$ . Khi đó: $a^{α} = \lim_{n \to + \infty} a^{r_{n}}$

2. Các tính chất của lũy thừa

Cho 2 số dương a, b; $m, n \in ℝ$ . Khi đó:

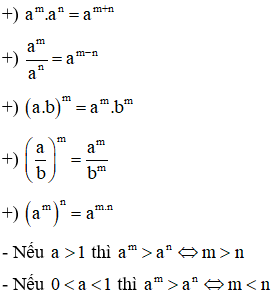
Công thức lũy thừa đầy đủ, chi tiết nhất - Toán lớp 12 (ảnh 1)

3. Một số tính chất của căn bậc n

• Với a, b ∈ R; n ∈ N*, ta có:

Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải

• Với a, b ∈ R ta có:

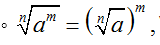
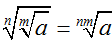
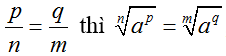
Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải , ∀ a > 0, n nguyên dương, m nguyên

Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải , ∀ a ≥ 0, n, m nguyên dương

Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải , ∀ a > 0, m,n nguyên dương, p, q nguyên. Đặc biệt

4. Bài tập vận dụng

Câu 1. Cho là số thực dương. Giá trị của biểu thức $P = a^{\frac{2}{3}} \sqrt{a}$ bằng

A. $a^{\frac{5}{6}}$

B. $a^{5}$

C. $a^{\frac{2}{3}}$

D. $a^{\frac{7}{6}}$ .

Lời giải

Chọn D

Với a >0, ta có:

$P = a^{\frac{2}{3}} \sqrt{a} = a^{\frac{2}{3}} a^{\frac{1}{2}} = a^{\frac{7}{6}}$ .

Câu 2. Rút gọn biểu thức $P = \frac{{(a^{\sqrt{3} - 1})}^{\sqrt{3} + 1}}{a^{4 - \sqrt{5}} . a^{\sqrt{5} - 2}}$ .

A. $P = 2$

B. $P = a^{2}$

C. $P = 1$

D. $P = a$ .

Lời giải

Chọn C

Ta có:

$P = \frac{{(a^{\sqrt{3} - 1})}^{\sqrt{3} + 1}}{a^{4 - \sqrt{5}} . a^{\sqrt{5} - 2}} = \frac{a^{(\sqrt{3} - 1) (\sqrt{3} + 1)}}{a^{4 - \sqrt{5} + \sqrt{5} - 2}} = \frac{a^{2}}{a^{2}} = 1$

Cách 2: sử dụng máy tính cầm tay

Nhập vào máy tính:

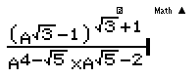
Các dạng bài tập về công thức lũy thừa – logarit – Toán lớp 12 (ảnh 1)

Sau đó bấm CALC thay một giá trị bất kì thỏa mãn a >0 và $a \neq 1$ và các đáp án phải khác nhau. Ta chọn A=3. Khi đó ta có kết quả.

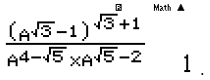
Các dạng bài tập về công thức lũy thừa – logarit – Toán lớp 12 (ảnh 1)

Câu 3. Với $α$ là một số thực bất kỳ, mệnh đề nào sau đây sai?

A. $\sqrt{10^{α}} = 10^{\frac{α}{2}}$

B. ${(10^{α})}^{2} = {(100)}^{α}$

C. $\sqrt{10^{α}} = {(\sqrt{10})}^{α}$

D. ${(10^{α})}^{2} = 10^{α^{2}}$

Lời giải

Chọn D

+) Có $\sqrt{10^{α}} = 10^{\frac{α}{2}}$ với mọi $α$ , nên A đúng.

+) Có ${(10^{α})}^{2} = {(100)}^{α}$ với mọi $α$ , nên B đúng.

+) Có $\sqrt{10^{α}} = {(\sqrt{10})}^{α}$ với mọi $α$ , nên C đúng.

+) Ta có ${(10^{α})}^{2} = 10^{2 α} \neq 10^{α^{2}}$ . Do đó D sai.

Câu 4. Biểu thức $P = \sqrt{x^{3} . \sqrt[3]{x^{2}}} . \sqrt[6]{x^{5}} (x > 0)$ viết dưới dạng lũy thừa với số mũ hữu tỷ là

A. $P = x^{\frac{8}{3}}$

B. $P = x^{\frac{5}{6}}$

C. $P = x^{\frac{1}{3}}$

D. $P = x^{3}$

Lời giải

Chọn A

Ta có:

$P = {(x^{3} {(x)}^{\frac{2}{3}})}^{\frac{1}{2}} . x^{\frac{5}{6}} = x^{\frac{3}{2}} . x^{\frac{1}{3}} . x^{\frac{5}{6}} = x^{\frac{8}{3}} .$

Câu 5. Tính giá trị biểu thức $A = {(\frac{1}{625})}^{\frac{- 1}{4}} + 16^{\frac{3}{4}} - 2^{- 2} {.64}^{\frac{1}{3}}$ .

A. 14.

B. 12.

C. 11.

D. 10.

Lời giải

Chọn B

Ta có

$A = 5^{(- 4) . \frac{- 1}{4}} + 2^{4. \frac{3}{4}} - 2^{- 2} {.2}^{6. \frac{1}{3}} = 5 + 2^{3} - 2^{0} = 12$

Câu 6. Cho a là số thực dương và $a \neq 1$ . Giá trị của biểu thức $M = {(a^{1 + \sqrt{2}})}^{1 - \sqrt{2}}$ bằng

A. $a^{2} .$

B. $a^{2 \sqrt{2}} .$

C. a

D. $\frac{1}{a} .$

Lời giải

Chọn D

Ta có:

$M = {(a^{1 + \sqrt{2}})}^{1 - \sqrt{2}} = a^{1 - 2} = a^{- 1} = \frac{1}{a}$

Vậy $M = \frac{1}{a}$ .

Câu 7. Cho $a > 0, a \neq 1$ , biểu thức $D = \log_{a^{3}} a$ có giá trị bằng bao nhiêu?

A. -3

B. 3

C. $\frac{1}{3}$

D. $- \frac{1}{3}$ .

Lời giải

Chọn C

Ta có:

$D = \log_{a^{3}} a = \frac{1}{3} \log_{a} a = \frac{1}{3}$

Câu 8. Với a và b là hai số thực dương, $a \neq 1$ . Giá trị của $a^{\log_{a} b^{3}}$ bằng

A. $b^{\frac{1}{3}}$

B. $\frac{1}{3} b$

C. 3b

D. $b^{3}$ .

Lời giải

Chọn D

Áp dụng công thức: $a^{\log_{a} b} = b$

Ta có: $a^{\log_{a} b^{3}} = b^{3}$ .

Câu 9. Tính giá trị của $a^{\log_{\sqrt{a}} 4}$ với $a > 0, a \neq 1$ .

A. 16

B. 8

C. 4

D. 2.

Lời giải

Chọn A

Ta có:

$a^{\log_{\sqrt{a}} 4} = a^{2 \log_{a} 4} = a^{\log_{a} 4^{2}} = 16$

Câu 10. Cho a là số thực dương khác 4. Tính $a^{\log_{\sqrt{a}} 4} = a^{2 \log_{a} 4} = a^{\log_{a} 4^{2}} = 16$ .

A. $I = - \frac{1}{3}$

B. $I = - 3$

C. $I = 3$

D. $I = \frac{1}{3}$ .

Lời giải

Chọn C

$I = \log_{\frac{a}{4}} (\frac{a^{3}}{64}) = \log_{\frac{a}{4}} {(\frac{a}{4})}^{3} = 3$

Tài liệu có 11 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm