Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Giao điểm là gì? Cách tìm giao điểm của 2 đường thằng, đường thẳng với mặt phẳng chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Giao điểm, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Giao điểm là gì? Cách tìm giao điểm của 2 đường thằng, đường thẳng với mặt phẳng

1. Giao điểm là gì?

Hai đường thẳng cắt nhau, hai đường thẳng chỉ có một điểm chung và điểm chung này được gọi là giao điểm của hai đường thẳng đó.

Nói một cách khác: Giao điểm của hai đường thẳng là điểm chung duy nhất của hai đường thẳng đó.

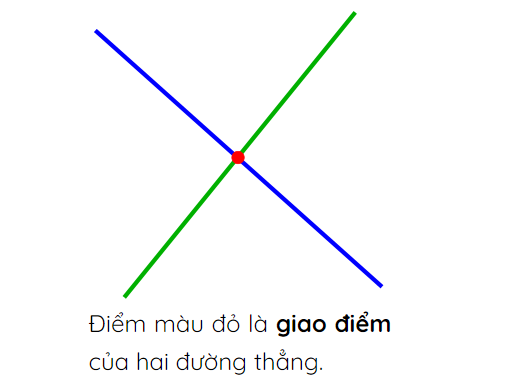
2. Các dạng toán về giao điểm của 2 đường thẳng

Dạng 1: Bài toán tìm giao điểm của 2 đường thẳng

*Phương pháp giải: Muốn tìm giao điểm của hai đường thẳng, ta xác định một điểm chung duy nhất của hai đường thẳng đó, khi đó điểm chung tìm được chính là giao điểm mà ta cần tìm.

Dạng 2: Bài tập tính số giao điểm

Ví dụ 1: Cho n (n>1) đường thẳng, biết hai đường thẳng bất kỳ nào trong n đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.

*Phương pháp giải:

Ta chọn ra 1 đường thẳng trong n đường thẳng đã cho, khi đó đường thẳng này sẽ cắt n-1 đường thẳng còn lại và số giao điểm được tạo ra là: n-1 (giao điểm);

Vì có n đường thẳng nên số giao điểm được tạo ra là: n * (n-1) (giao điểm);

Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: n * (n-1) : 2 (giao điểm).

Đáp số: Số giao điểm cần tính là n * (n-1) : 2 giao điểm.

Ví dụ 2: Cho 10 đường thẳng, biết hai đường thẳng bất kỳ nào trong 10 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng 

Phương pháp giải

Ta chọn ra 1 đường thẳng trong 10 đường thẳng đã cho, khi đó đường thẳng này sữ cắt 9 đường thẳng còn lại và số giao điểm được tạo ra là: 9 (giao điểm);

Vì có 10 đường thẳng nên số giao điểm được tạo ra là: 10 * 9 = 90 (giao điểm);

Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 90 : 2 = 45 (giao điểm).

Đáp số : Số giao điểm cần tính là 45 giao điểm.

Bài tập vận dụng:

Cho 32 đường thẳng, biết hai đường thẳng bất kỳ nào trong 32 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.

3. Cách tìm giao điểm của đường thẳng và mặt phẳng

Phương pháp giải

Muốn tìm giao điểm của đường thẳng d và mặt phẳng (P), có hai cách làm như sau:

* Cách 1:

    + Những bài đơn giản, có sẵn một mặt phẳng (Q) chứa đường thẳng d và một đường thẳng a nào đó thuộc mặt phẳng (P)

    + Trong mp( Q), 2 đường thẳng a và d cắt nhau tai điểm A. Khi đó điểm A chính là giao điểm của đường thẳng d và mp(P)

* Cách 2: Chọn mặt phẳng phụ:

    + Tìm một mặt phẳng (Q) chứa đường thẳng d, sao cho dễ dàng tìm giao tuyến của mp (Q) với mp (P)

    + Tìm giao tuyến của mp(P) và (Q) - gọi là đường thẳng d.

    + Tìm giao điểm của đường thẳng a và đường thẳng d - gọi là điểm A

Khi đó: điểm A chính là giao điểm của đường thẳng d và mp (P)

Ví dụ minh họa

Ví dụ 1: Cho 4 điểm A, B, C, D không đồng phẳng và không có 3 điểm nào thẳng hàng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD. Giao điểm của đường thẳng CD và mp(MNP) là giao điểm của

A. CD và NP 

B. CD và MN

C. CD và MP   

D. CD và AP

Lời giải

Cách 1.

   + Chọn mặt phẳng phụ chứa CD là mp(BCD)

   + Do NP không song song CD nên NP cắt CD tại E

Điểm E ∈ NP nên E ∈ (MNP)

⇒ giao điểm của CD và mp(MNP) là điểm E.

Chọn A.

Cách 2

   + Ta có : NP ⊂ (BCD)

⇒ NP và CD đồng phẳng

   + Gọi E là giao điểm của NP và CD mà NP ⊂ ( MNP)

suy ra CD ∩ (MNP) = E

Vậy giao điểm của CD và mp (MNP) là giao điểm E của NP và CD.

Ví dụ 2: Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là:

A. Điểm F

B. Giao điểm của đường thẳng EG và AF.

C. Giao điểm của đường thẳng EG và AC.

D. Giao điểm của đường thẳng EG và CD.

Lời giải

   + Vì G là trọng tâm tam giác BCD; F là trung điểm của CD nên G ∈ BF ⊂ (ABF)

   + Ta có E là trung điểm của A B nên E ∈ (ABF).

   + chọn mp phụ chứa EG là (ABF).

Dễ dàng tìm được giao tuyến của (ACD) và (ABF) là AF.

   + Trong mp(ABF); gọi M là giao điểm của EG và AF .

Vậy giao điểm của EG và mp(ACD) là giao điểm M của EG và AF

Chọn B

Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC. Gọi I là giao điểm của AM với mp (SBD) . Tìm mệnh đề đúng?

A. IA→ = -2IM→

B. IA→ = -3IM→

C. IA→ = 2IM→

D. tất cả sai

Lời giải

   + Gọi O là tâm hình bình hành ABCD suy ra O là trung điểm của AC.

   + Nối AM cắt SO tại I mà SO ⊂ (SBD)

Suy ra I = AM ∩ (SBD).

   + Tam giác SAC có M; O lần lượt là trung điểm của SC và AC

Mà I là giao điểm của AM và SO.

⇒ I là trọng tâm tam giác SAC

⇒ AI = 2/3 AM và IA = 2.IM

Lại có điểm I nằm giữa A và M suy ra: IA→ = -2IM→

Chọn A

4. Giao điểm trong tam giác

- Ba đường trung tuyến của tam giác cùng đi qua 1 điểm. Điểm này cách các đỉnh của tam giác một đoạn bằng 2/3 độ dài của chính các đường trung tuyến đi qua đỉnh đó. Giao điểm này được gọi là trọng tâm.

- Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác.

- Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

- Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này gọi là trực tâm của tam giác

5. Bài tập về giao điểm

Bài 1: Cho ba điểm S, Q, T không thẳng hàng. Em hãy vẽ các đường thẳng SQ, ST và QT và cho biết ba điểm S, Q, T lần lượt là giao điểm của cặp đường thẳng nào?

Hướng dẫn giải:

Điểm S là giao điểm của đường thẳng SQ và đường thẳng ST;

Điểm Q là giao điểm của đường thẳng SQ và đường thẳng QT;

Điểm T là giao điểm của đường thẳng ST và đường thẳng QT.

Bài 2: Cho 218 đường thẳng, biết hai đường thẳng bất kỳ nào trong 218 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.

Hướng dẫn giải: 

Ta chọn ra 1 đường thẳng trong 218 đường thẳng đã cho, khi đó đường thẳng này sẽ cắt 217 đường thẳng còn lại và số giao điểm được tạo ra là 217 (giao điểm);

Vì có 218 đường thẳng nên số giao điểm được tạo ra là: 218 * 217 = 47306 (giao điểm);

Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 47306 : 2 = 23653 (giao điểm).

Đáp số: Số giao điểm cần tính là 23653 giao điểm

Bài 3: Cho tứ giác ABCD có AC và BD giao nhau tại O; điểm S không thuộc mp(ABCD). Trên đoạn SC; lấy 1 điểm M không trùng với S và C. Gọi K là giao điểm của SO và AM. Giao điểm của đưởng thẳng SD và mp( ABM) là :

A. Giao điểm của SD và AB

B. Giao điểm của SD và AM

C. Giao điểm của SD và BK

D. Giao điểm của SD và MK

Lời giải

   + Chọn mặt phẳng phụ chứa SD là mp(SBD)

   + Ta tìm giao tuyến của hai mặt phẳng (SBD) và (ABM)

Ta có: B ∈ (SBD) ∩ (ABM)    (1)

Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD .

Trong mặt phẳng (SAC), gọi K là giao điểm của AM và SO.

Ta có:

- K ∈ SO ⊂ (SBD)

- K ∈ AM ⊂ (ABM)

⇒ K ∈ (SBD) ∩ (ABM)     (2)

Từ (1) và (2) suy ra: giao tuyến của (ABM) và (SBD) là BK

   + Trong mặt phẳng (SBD), gọi N là giao điểm của SD và BK

⇒ N là giao điểm của SD và mp (ABM)

Chọn C

Bài 4: Cho 4 điểm A, B, C và S không cùng thuộc 1 mặt phẳng. Gọi I và H lần lượt là trung điểm của SA và AB. Trên SC lấy điểm K sao cho IK không song song với AC. Gọi E là giao điểm của đường thẳng BC với mp(IHK). Chọn mệnh đề đúng?

A. Điểm E thuộc tia BC

B. Điểm E thuộc tia CB

C. Điểm E nằm trong đoạn BC

D. Điểm E nằm giữa B và C

Lời giải

   + Chọn mặt phẳng phụ chứa BC là mp (ABC)

   + Tìm giao tuyến của hai mặt phẳng (ABC) và (IHK)

- H ∈ (ABC) ∩ (IHK)    (1)

Trong mặt phẳng (SAC), do IK không song song với AC nên gọi giao điểm của IK và AC là F. Ta có

- F ∈ AC ⊂ (ABC)

- F ∈ IK ⊂ (IHK)

Suy ra: F ∈ (ABC) ∩ (IHK)    (2)

Từ (1) và (2) suy ra: HF = (ABC) ∩ (IHK)

   + Trong mặt phẳng (ABC), gọi E là giao điểm của HF và BC

Ta có

- E ∈ HF ⊂ (IHK)

- E ∈ BC

⇒ giao điểm của BC và (IHK) là E.

Chọn D

Bài 5: Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Trên AB; AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây:

A. (BCD)       

B. (ABD)      

C. (CMN)      

D. (ACD)

Lời giải

Chọn D

   + Do I là giao điểm của MN và BD nên:

I ∈ BD ⇒ I ∈ (BCD), (ABD)

I ∈ MN ⇒ I ∈ (CMN)

Bài 6: Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SC, N là trên cạnh BC. Gọi O = AC ∩ BD, J = AN ∩ BD và gọi I = SO ∩ AM. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)

A. là giao điểm của SD và SI

B. là giao điểm của SD và BJ

C. Là giao điểm của SD và MI

D. là giao điểm của SD và IJ

Lời giải

Trong mp (SBD), gọi K = IJ ∩ SD

Ta có I ∈ AM ⊂ (AMN), J ∈ AN ⊂ (AMN)

⇒ IJ ⊂ (AMN)

Do đó K ∈ IJ ⊂ (AMN) ⇒ K ∈ (AMN)

Vậy K = SD ∩ (AMN)

Chọn D

Bài 7: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi I, K là 2 điểm trên SA; BC. Gọi E là giao điểm của AK và BD; O là giao điểm của AC và BD. Tìm giao điểm của IK với (SBD) ?

A. Là giao điểm của IK và SO

B. Là giao điểm của IK và DO

C. Là giao điểm của IK và SE

D. Là giao điểm của IK và BE

Lời giải

   + Chọn mp(SAK) chứa IK. Tìm giao tuyến của (SAK) và (SBD)

Có S ∈ (SAK) ∩ (SBD)    (1)

   + Trong mp(ABCD) có:

   + Từ (1) và (2) suy ra (SAK) ∩ (SBD) = SE

   + Trong mp(SAK) gọi

Vậy giao điểm của IK và (SBD) là giao điềm của IK và SE

Chọn C

Bài 8: Cho tứ diện ABCD. Các điểm P; Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD. Tính tỉ số: SA/SD

A. 2      

B. 1      

C. 1/2      

D. 1/3

Lời giải

   + Gọi I là giao điểm của BD và RQ. Nối P với I; cắt AD tại S

   + Xét tam giác BCD bị cắt bởi IR, ta có

   + Xét tam giác ABD bị cắt bởi PI ta có:

Chọn A.

Bài 9: Cho tứ diện ABCD và ba điểm P; Q: R lần lượt lấy trên ba cạnh AB; CD; BC. Cho PR// AC và CQ = 2.QD. Gọi giao điểm của AD và (PQR) là S. Chọn khẳng định đúng?

A. AD = 3 DS   

B. AD = 2 DS   

C. AS = 3 DS   

D. AS = DS

Lời giải

   + Gọi I là giao điểm của BD và RQ. Nối P với I; cắt AD tại S

   + Vì PR song song với AC suy ra:

⇒ AD = 3.DS

Chọn A

Bài 10: Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên cạnh SA. Tìm giao điểm của đường thẳng SB với mặt phẳng (MCD).

A. Điểm H, trong đó E = AB ∩ CD, H = SA ∩ EM

B. Điểm N, trong đó E = AB ∩ CD, N = SA ∩ EM

C. Điểm F, trong đó E = AB ∩ CD, F = SA ∩ EM

D. Điểm T, trong đó E = AB ∩ CD, T = SA ∩ EM

Lời giải:

Trong mặt phẳng (ABCD), gọi E = AB ∩ CD

Trong (SAB) gọi N là giao điểm của ME và SB.

Ta có: N ∈ EM ⊂ (MCD) ⇒ N ∈ (MCD)    (1)

Lại có: N ∈ SB     (2)

Từ (1) và (2) suy ra: N = SB ∩ (MCD)

Chọn B

Bài 11: Tìm tọa độ giao điểm của các đường thẳng sau:

a) d: y = 3x – 2 và d’: y = 2x + 1;

b) d: y = 4x – 3 và d’: y = 2x + 1.

Lời giải:

a) Phương trình hoành độ giao điểm của d và d’ là:

3x – 2 = 2x + 1

$\iff 3x-2x=1+2$

$\iff x=3$

Thay x = 3 và d ta được:

$y=3.3-2=9-2=7$

Vậy tọa độ giao điểm của d và d’ là A(3; 7).

b) Phương trình hoành độ giao điểm của d và d’ là:

4x – 3 = 2x + 1

$\iff 4x-2x=3+1$

$\iff 2x=4$

$\iff x=2$

Thay x vào d ta được: $y=4.2-3=5$

Vậy tọa độ giao điểm của d và d’ là B(2; 5).

Bài 12: Tìm tham số m để:

a) d: y = 2mx + 5 và d’: y = 4x + m cắt nhau tại điểm có hoành độ bằng 1.

b) d: y = (3m – 2)x – 4 cắt trục hoành tại điểm có hoành độ bằng 3.

Lời giải:

a) Phương trình hoành độ giao điểm của d và d’ là:

2mx + 5 = 4x + m.

Vì hai đường thẳng d và d’ cắt nhau tại điểm có hoành độ bằng 1 nên thay x = 1 vào phương trình hoành độ giao điểm ta có:

2m.1 + 5 = 4.1 + m

$\iff 2m+5=4+m$

$\iff 2m-m=4-5$

$\iff m=-1$

Vậy m = -1 thì d và d’ cắt nhau tại điểm có hoành độ bằng 1.

b) Vì d cắt trục hoành tại điểm có hoành độ bằng 3 nên giao điểm của d với trục hoành là A(3; 0). Thay tọa độ điểm A vào d ta được:

0 = (3m – 2).3 – 4

$\iff 0=9m-6-4$

$\iff 9m=10$

$\iff m=\frac{10}{9}$

Vậy $m=\frac{10}{9}$ thì d cắt trục hoành tại điểm có hoành độ bằng 3.