Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Hình chiếu là gì? Cách tìm Hình chiếu của một điểm lên đường thẳng, mặt phẳng, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Hình chiếu, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Hình chiếu là gì? Cách tìm Hình chiếu của một điểm lên đường thẳng, mặt phẳng

A. Lý thuyết Hình chiếu

1. Hình chiếu là gì?

Hình chiếu là hình biểu diễn ba chiều của đối tượng lên mặt phẳng hai chiều. Yếu tố cơ bản giúp tạo nên chiếu chính là đối tượng cần chiếu, mặt phẳng chiếu và phép chiếu.

Hình chiếu của một đoạn thẳng nằm trên đường chiếu chính là khoảng cách giữa hai đoạn thẳng vuông góc với đường thẳng đã cho trước. Hình chiếu của một điểm tức là giao điểm của đường thẳng đã cho trước, và đường thẳng kẻ từ điểm vuông góc.

2. Cách tìm hình chiếu của 1 điểm lên đường thẳng, mặt phẳng

- Cách xác định hình chiếu vuông góc của điểm:

Trong không gian cho điểm M và mặt phẳng (α). Điểm H gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (α) nếu H ∈ (α) và MH ⊥ (α).

→ Để tìm hình chiếu vuông góc của điểm M lên mặt phẳng (α) ta dựng đường thẳng d qua M và vuông góc với mặt phẳng (α) sau đó tìm giao điểm H của d và (α). Nếu M ∈ (α) thì hình chiếu của M là chính nó.

Cách tìm hình chiếu của 1 điểm lên đường thẳng

Cho trước điểm A(x₀; y₀) và phương trình đường thẳng d: ax + by + c = 0 có VTPT $\overrightarrow{n}(a,b)$. Tìm hình chiếu của điểm A lên đường thẳng d:

+ Bước 1: Gọi H là hình chiếu của A lên đường thẳng d.

+ Bước 2: Lập phương trình tổng quát của AH

AH: 

⇒ phương trình AH: b(x - x₀) - a(y - y₀) = 0

+ Bước 3: AH và d cắt nhau tại H nên tọa độ điểm H là nghiệm hệ phương trình:

Từ hệ phương trình trên ta suy ra tọa độ điểm H.

Cách tìm hình chiếu của 1 điểm lên mặt phẳng

Cách xác định hình chiếu của 1 điểm A lên mặt phẳng (P)

- Viết phương trình đường thẳng đi qua A và vuông góc với (P)

- Tìm H là giao điểm của d và (P) => H là giao điểm của A trên (P)

- Cách xác định hình chiếu vuông góc của đường thẳng:

Trong không gian cho mặt phẳng (α) và đường thẳng d không vuông góc với mặt phẳng (α). Để tìm hình chiếu vuông góc của d lên (α) ta chọn hai điểm A, B trên d rồi tìm hình chiếu K, H lần lượt của A, B lên (α). Đường thẳng a trong (α) đi qua hai điểm H, K chính là hình chiếu vuông góc của đường thẳng d lên mặt phẳng (α).

Ví dụ 1. Cho hình chóp tam giác S.ABC có SA ⊥ (ABC).

a) Xác định hình chiếu vuông góc của điểm S lên mặt phẳng (ABC).

b) Xác định hình chiếu vuông góc của đường thẳng SB lên mặt phẳng (ABC).

c) Xác định hình chiếu vuông góc của tam giác SBC lên mặt phẳng (ABC).

Hướng dẫn giải

a) Vì SA ⊥ (ABC) và A ∈ (ABC) nên A là hình chiếu vuông góc của điểm S lên mặt phẳng (ABC).

b) Vì B ∈ (ABC) nên hình chiếu vuông góc của B lên mặt phẳng (ABC) là B, hình chiếu vuông góc của S lên (ABC) là A (theo phần a) nên hình chiếu vuông góc của đường thẳng SB lên (ABC) là đường thẳng AB.

c) B, C ∈ (ABC) nên hình chiếu vuông góc của B, C lên mặt phẳng (ABC) lần lượt là B, C. 

Hình chiếu vuông góc của S lên (ABC) là A (theo phần a).

Do đó, hình chiếu vuông góc của tam giác SBC lên (ABC) là tam giác ABC.

Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, gọi O là giao điểm của hai đường chéo AC, BD, M là trung điểm của SB. Biết SO ⊥ (ABCD).

a) Xác định hình chiếu vuông góc của SM trên mặt phẳng (ABCD).

b) Xác định hình chiếu vuông góc của O trên mặt phẳng (SAB).

Hướng dẫn giải

a) Vì SO ⊥ (ABCD) nên dựng đường thẳng d qua M song song với SO thì d ⊥ (ABCD).

Vì S, O, M đều thuộc mặt phẳng (SOB) nên d ⊂ (SOB).

M ∈ SB, d // SO nên d cắt OB. Gọi giao điểm của d và OB là N.

Xét tam giác SOB có:

MN // SO

M là trung điểm của SB

Do đó, N là trung điểm của OB (theo định lí đường trung bình).

Suy ra với N là trung điểm của OB thì MN ⊥ (ABCD) nên N là hình chiếu vuông góc của M lên (ABCD).

Hình chiếu vuông góc của S lên (ABCD) là O (vì SO ⊥ (ABCD)).

Vậy hình chiếu vuông góc của SM lên (ABCD) là ON.

b)

Kẻ OK ⊥ AB (K ∈ AB), nối SK, từ O kẻ OH ⊥ SK (H ∈ SK).

Ta có:

SO ⊥ (ABCD) ⇒ SO ⊥ AB

OK ⊥ AB (K ∈ AB) (do cách vẽ)

SO, OK ⊂ (SOK)

SO ∩ OK tại O

Do đó, AB ⊥ (SOK)

⇒ AB ⊥ SH (vì OH ∈ (SOK))

Mà: OH ⊥ SK (cách vẽ)

SK, AB ⊂ (SAB); SK ∩ AB tại K

Suy ra: OH ⊥ (SAB).

Vậy H là hình chiếu vuông góc của O lên (SAB).

B. Bài tập Hình chiếu

1. Bài tập trắc nghiệm

Ví dụ 1: Cho điểm A( 1; 2) và đường thẳng (d): x + 2y - 3 = 0 .Tìm hình chiếu của A lên đường thẳng d.

A. ( 1; -2)    

B. (-  ;  )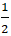    

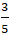
C. (  ;  )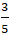    

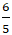
D. Đáp án khác

Lời giải

+ Gọi H là hình chiếu của A lên đường thẳng (d) .

+ Lập phương trình đường thẳng AH:

(AH) : 

⇒ Phương trình ( AH) : 2(x - 1) – 1.( y - 2) = 0 hay 2x - y = 0

+ Hai đường thẳng AH và d cắt nhau tại H nên tọa độ điểm H là nghiệm hệ phương trình:

Chọn C.

Ví dụ 2: Cho điểm A( 2; 0) và đường thẳng d: x + y - 2 = 0. Tìm hình chiếu của điểm A lên đường thẳng d.

A. ( 2; -1)    

B. (2; 0)    

C. (1; -2)    

D. (-2; -1)

Lời giải

Ta có: 2 + 0 - 2 = 0 nên điểm A thuộc đường thẳng d.

⇒ Hình chiếu của điểm A lên đường thẳng d chính là điểm A.

Chọn B.

Ví dụ 3: Cho tam giác ABC có A( 0; -2).Gọi I ( 2; 4) là trung điểm của AB và J( -4; 2) là trung điểm của AC. Gọi hình chiếu của điểm A lên BC là H. Viết phương trình đường thẳng AH?

A. 6x + 2y - 3 = 0    

B. 6x + 2y + 4 =0    

C. 2x - y + 1 = 0    

D. Tất cả sai

Lời giải

+ Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC ⇒ IJ// BC ( 1) .

+ Do H là hình chiếu của A lên BC

⇒ AH vuông góc BC (2).

Từ(1) và ( 2) suy ra: AH vuông góc IJ

+ Lập phương trình AH: 

⇒ ( AH): 6(x - 0) + 2( y + 2) = 0 hay 6x + 2y + 4 = 0.

Chọn B.

Ví dụ 4: Toạ độ hình chiếu của M(4; 1) trên đường thẳng ∆: x - 2y + 4 = 0 là:

A. ( 14; -19)    

B. ( 2; 3)    

C. ( ;  )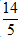    

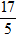
D. (-  ;  )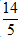

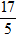
Lời giải

+ Đường thẳng ∆ có 1 VTPT n→(1; -2)

Gọi H( 2t - 4; t) là hình chiếu của M trên đường thẳng ∆ thì MH→(2t - 8; t - 1)

⇒ Hai vecto MH→ và n→(2; -3) cùng phương nên:

 ⇒ H( ;  )

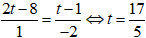
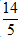
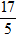
Chọn C.

Ví dụ 5: Cho đường thẳng ∆: 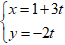 và điểm M(3; 3) . Tọa độ hình chiếu vuông góc của M trên đường thẳng ∆ là:

A. (4; -2)    

B. (1; 0)    

C. (-2; 2)    

D. (7; -4)

Lời giải

Gọi H là hình chiếu của M trên ∆.

Ta có: H ∈ ∆ ⇒ H(1 + 3t; - 2t), MH→ = (- 2 + 3t; - 3 - 2t)

Đường thẳng có vectơ chỉ phương là u→( 3; -2) .

Do H là hình chiếu vuông góc của M trên ∆ nên hai đường thẳng MH và ∆ vuông góc với nhau

⇒ MH→.u→ = 0 ⇔ 3( -2 + 3t ) – 2( -3 - 2t) = 0

⇔ -6 + 9t + 6 + 4t = 0 ⇔ 13t = 0 ⇔ t = 0

⇒ H ( 1; 0)

Chọn B.

Ví dụ 6: Tìm hình chiếu của A( 3;-4) lên đường thẳng d: 

A. ( 1; 2)    

B. (4; -2)    

C. ( -1; 2)    

D. ( -1; -3)

Lời giải

+ Lấy điểm H(2 + 2t; -1 - t) thuộc d.

Ta có AH→ = (2t - 1; -t + 3)

Vectơ chỉ phương của d là u→( 2; -1)

+Do H là hình chiếu của A trên d

⇔ AH ⊥ d ⇔ u→.AH→ = 0 ⇔ 2(2t - 1) - (- t + 3) = 0 ⇔ t = 1

+ Với t = 1 ta có H( 4; -2)

Vậy hình chiếu của A trên d là H( 4; -2).

Chọn B.

Ví dụ 7: Cho đường thẳng ∆: 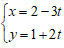 . Hoành độ hình chiếu của M( 4; 5) trên ∆ gần nhất với số nào sau đây ?

A. 1,1    

B. 1,2    

C. 1,3    

D. 1,5

Lời giải

Gọi H là hình chiếu của M trên ∆.

Ta có: H ∈ ∆ nên H( 2 - 3t; 1 + 2t) và MH→( -2 - 3t; -4 + 2t)

Đường thẳng ∆có vectơ chỉ phương là u→(3; - 2) .

u→ ⊥ MH→ ⇔ u→.MH→ = 0 ⇔ 3(-2 - 3t) - 2(-4 + 2t) = 0 ⇔ -13t + 2 = 0 ⇔ t = 
⇒ H( ;  )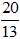

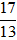
⇒ Hoành độ của điểm H là  .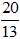

Chọn D.

Ví dụ 8: Cho tam giác BAC có AB = 3; BC = 3√3 và góc B = 30⁰.Gọi H là hình chiếu của A lên BC. Tìm mệnh đề đúng?

A. H nằm trong đoạn BC thỏa mãn: BH = 2 HC

B. AH =  .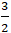

C. BH = 2.

D. Tất cả sai

Lời giải

+ Áp dụng định lí cosin vào tam giác ABC ta có:

AC² = AB² + BC² – 2.AC.BC.Cos B

= 3² + (3√3 )² - 2.3.3√3.cos30⁰ = 9

⇒ AC = 3 nên AB = AC = 3

⇒ Tam giác BAC cân tại A.

+ AH là đường cao nên đồng thời là đường trung tuyến

⇒ H là trung điểm của BC: BH = CH = 

+ Xét tam giác vuông AHB có: AH = AB.sinB = 3.sin30⁰ = 1,5.

Chọn B.

2. Bài tập vận dụng

Ví dụ 1: Cho đường thẳng d: x - y = 0 và điểm M(1; 3). Tìm hình chiếu của M trên d?

A. (1; 3)    

B. (2; 2)    

C. ( 3; -1)    

D. (4; -1)

Lời giải

+ Gọi H(a;b) là hình chiếu của M trên d.

+ Do H thuộc d nên a - b = 0 (1)

+ Ta có: MH→(a - 1; b - 3).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→ (1; -1)

⇒  ⇔ -a + 1= b - 3 hay a + b = 4 (2)

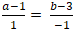
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(2; 2).

Chọn B.

Ví dụ 2: Cho đường thẳng d: 2x - y + 3 = 0 và điểm M(0; 4). Tìm hình chiếu của M trên d?

A. H(-  ;  ).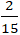    

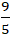
B. H( ;  ).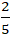    

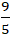
C. H( ;  ).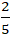    

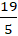
D. (4; -1)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 2a - b + 3 = 0 (1)

+ Ta có: MH→(a; b - 4).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a = 2b - 8 hay a + 2b = 8 (2)

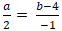
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H( ;  )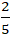

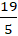
Chọn C.

Ví dụ 3: Cho đường thẳng d: x + 2y + 4 = 0 và điểm M(1; 3). Gọi M’(x; y) là điểm đối xứng với M qua d. Tính 2x - y?

A. 1    

B. 2    

C. 0    

D. -1

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên a + 2b + 4 = 0 (1)

+ Ta có: MH→(a - 1; b - 3).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(1 ; 2)

⇒  ⇔ 2a - 2 = b - 3 hay 2a - b = -1 (2)

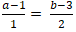
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(-1,2; -1,4).

+ Gọi M’đối xứng với M qua d thì H là trung điểm MM’ nên tọa độ điểm M’:

Vậy M’(-3,4; - 5,8) ⇒ 2x - y = -1

Chọn D.

Ví dụ 4: Cho đường thẳng d: 2x - y = 0 và điểm M(1 ;0). Gọi M’ (x; y) là điểm đối xứng với M qua d. Tính 4x + 3y?

A. 1    

B. 2    

C. 0    

D. -1

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 2a - b = 0 (1)

+ Ta có: MH→(a-1; b).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a + 1 = 2b hay a + 2b = 1 (2)

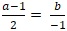
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(0,2; 0,4).

+ Gọi M’đối xứng với M qua d thì H là trung điểm MM’ nên tọa độ điểm M’:

Vậy M’(-0,6; 0,8) ⇒ 4x + 3y = 0

Chọn C.

Ví dụ 5: Cho đường thẳng d: 2x - 3y + 5 = 0 và điểm A(-1; 1). Tìm hình chiếu của điểm A trên d?

A. (2; -1)    

B. (-2; -1)    

C. (-1; 1)    

D. (-1; 3)

Lời giải

Thay tọa độ điểm A vào phương trình đường thẳng d ta được :

2.(-1) - 3.1 + 5 = 0

⇒ Điểm A thuộc đường thẳng d nên hình chiếu của điểm A trên đường thẳng d là chính nó.

Chọn C.

Ví dụ 6: Cho đường thẳng (d): x + y - 3 = 0 và điểm M(2; 1) thuộc (d). Tập hợp những điểm A( x; y) sao cho M là hình chiếu của A trên d là đường thẳng nào?

A. x + y - 4 = 0    

B. x + y - 1 = 0    

C. x - y - 1 = 0    

D. x - y + 3 = 0

Lời giải

+ Đường thẳng (d) có VTPT n→( 1; 1).

+ Vecto MA→( x - 2; y - 1).

Do M là hình chiếu của A trên d nên MA vuông góc d

⇒ Hai vecto MA→ và n_d→ cùng phương

⇔  ⇔ x - 2 = y - 1 hay x - y - 1 = 0

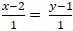
Vậy tập hợp những điểm A sao cho M là hình chiếu của A trên d là đường thẳng:
∆: x - y - 1 = 0

Chọn C.

Ví dụ 7: Cho đường thẳng d: 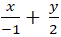 = 1 và điểm M(0; 3). Tìm hình chiếu của M trên d?

A. (1; 3)    

B. (0,4; 2,8)    

C. ( 2,3; -1)    

D. (4; -1,2)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 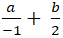 = 1 hay 2a - b = -2 (1)

+ Ta có: MH→(a; b - 3). Phương trình tổng quát (d): 2x - y + 2 = 0

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a = 2b - 6 hay a + 2b = 6 (2)

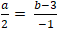
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(0,4; 2,8)

Chọn B.

Ví dụ 8: Cho đường thẳng d: x - y + 3 = 0 và điểm M(1; 1). Tìm hình chiếu của M trên d?

A. H(-  ;  ).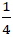    

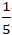
B. H( ;  ).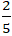    

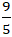
C. H( ;  ).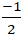   

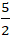
D. (4; -1)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên a- b+3= 0 (1)

+ Ta có: MH→(a - 1; b - 1).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(1; -1)

⇒  ⇔ -a + 1 = b - 1 hay a + b = 2 (2)

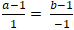
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H( ;  ).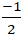

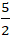
Chọn C.

Ví dụ 9: Cho đường thẳng d: 4x + y - 5 = 0 và điểm A(1; 1). Tìm hình chiếu của điểm A trên d?

A. (2; -1)    

B. (-2; -1)    

C. (1; 1)    

D. (-1; 3)

Lời giải

Thay tọa độ điểm A vào phương trình đường thẳng d ta được :

4.1 + 1 - 5 = 0

⇒ Điểm A thuộc đường thẳng d nên hình chiếu của điểm A trên đường thẳng d là chính nó.

Chọn C.

Ví dụ 10: Cho đường thẳng (d): 2x + 3y - 3 = 0 và điểm M(0; 1) thuộc (d). Tập hợp những điểm A( x; y) sao cho M là hình chiếu của A trên d là đường thẳng nào?

A. 2x + 3y - 4 = 0    

B. 3x - 2y + 2 = 0    

C. 3x - 2y - 1 = 0    

D. 2x - 3y + 3 = 0

Lời giải

+ Đường thẳng (d) có VTPT n→(2; 3).

+ Vecto MA→( x; y - 1).

Do M là hình chiếu của A trên d nên MA vuông góc d

⇒ Hai vecto MA→ và n→ cùng phương

⇔  ⇔ 3x = 2y - 2 hay 3x - 2y + 2 = 0

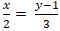
Vậy tập hợp những điểm A sao cho M là hình chiếu của A trên d là đường thẳng: ∆: 3x - 2y + 2 = 0

Chọn B.

Ví dụ 11. Cho tam giác OBC có O(0; 0) ; B( 0; 6) và C(-6; 0). Gọi G là trọng tâm tam giác OBC. Tìm điểm G’ đối xứng với G qua BC?

A. G’( -  ;-  )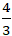    

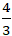
B. G’( -1; 1)    

C. G’(-2; 2)    

D. G’(-4; 4)

Lời giải

+ ta có: OB→(0; 6); OC→( -6; 0)

⇒ OB= 6; OC= 6 và OB→.OC→ = 0.(-6) + 6.0 = 0

⇒ OB vuông góc OC và OB = OC

⇒ Tam giác OBC vuông góc tại O.

+ Do G là trọng tâm tam giác OBC nên tọa độ điểm G:

 ⇒ G( -2; 2)

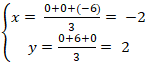
+ Gọi M là trung điểm của BC. Do tam giác OBC là vuông cân tại O nên đường trung tuyến OM đồng thời là đường cao nên OM vuông góc BC tại M.

⇒ G’ đối xứng với G qua BC nên M là trung điểm của GG’.

- M là trung điểm BC nên tọa độ điểm M: 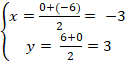 ⇒ M( - 3; 3)

- M là trung điểm GG’nên tọa độ điểm G’ là:

 ⇒ G’ ( -4; 4)

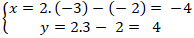
⇒ Vậy tọa độ điểm G’( - 4; 4)

Chọn D.

3. Bài tập tự luyện

Câu 1. Khẳng định nào sau đây là đúng?

A. Nếu MH ⊥ (P) tại H thì M là hình chiếu vuông góc của H lên (P);

B. Nếu MH ⊥ (P) tại H thì H là hình chiếu vuông góc của M lên (P);

C. Nếu MH // (P) thì M là hình chiếu vuông góc của H lên (P);

D. Nếu MH // (P) thì H là hình chiếu vuông góc của M lên (P).

Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông góc với mặt đáy. Hình chiếu vuông góc của SD lên mặt phẳng (ABCD) là:

A. SB;        

B. CD;                 

C. AD;                 

D. BD.

Câu 3. Cho hình chóp S.MNPQ, A là trung điểm của MN. Biết SA vuông góc với đáy. Hình chiếu vuông góc của SM lên mặt phẳng (MNPQ) là:

A. AN;                 

B. AM;                

C. MN;                

D. MQ.

Câu 4.  Cho hình chóp S.MNPQ, A là trung điểm của MN, B là trung điểm của SP. Biết SA vuông góc với đáy. Hình chiếu vuông góc của SB lên mặt phẳng (MNPQ) là:

A. AC với C là trung điểm của PQ;

B. AC với C là trung điểm của MP;

C. AC với C là trung điểm của AQ;

D. AC với C là trung điểm của AP.

Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông góc với mặt đáy. Hình chiếu vuông góc của tam giác SCD lên mặt phẳng (ABCD) là:

A. ∆ACD;  

B. ∆BCD;  

C. ∆BAD;  

D. ∆ABC.

Câu 6. Cho hình chóp S.MNPQ, A là trung điểm của MN, B là trung điểm của SP, C là trung điểm của SQ. Biết SA vuông góc với đáy. Hình chiếu vuông góc của tam giác SBC lên mặt phẳng (MNPQ) là:

A. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, BQ;

B. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, AQ;

C. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, AN;

D. Tam giác AB'C' với B', C' lần lượt là trung điểm của AM, AQ.

Câu 7. Cho hình chóp S.ABCD có SA = SB = SC = AB = AC = a, BC = $a\sqrt{2}$. Hình chiếu vuông góc của S lên (ABCD) là điểm H sao cho:

A. H là trung điểm của AB;

B. H trùng với C;

C. H là trung điểm của BC;

D. H trùng với A.

Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy. Hình chiếu vuông góc của SC lên mặt phẳng (SAB) là:

A. SB;

B. SM với M là trung điểm của AB;

D. SA;

D. SN với N là trung điểm của SB.

Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với (ABCD). Hình chiếu của BD lên (SAD) là:

A. ID với I là trung điểm SA;

B. BA;

C. ID với I là trọng tâm của tam giác SAD;

D. SD.

Câu 10. Hình chóp tam giác đều S.ABC có cạnh bên bằng cạnh đáy. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là:

A. Điểm H với H là trọng tâm của tam giác ABC;

B. Điểm H với H là trung điểm AB;

C. Điểm H với H là trung điểm BC;

D. Điểm H với H là trung điểm AC.