Căn bậc hai là gì? Căn bậc hai số học là gì? Các dạng bài tập về căn bậc hai

Van Anh Ngày: 13-11-2024 Tổng hợp kiến thức

Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Căn bậc hai là gì? Căn bậc hai số học là gì? Các dạng bài tập về căn bậc hai, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Căn bậc hai, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Căn bậc hai là gì? Căn bậc hai số học là gì? Các dạng bài tập về căn bậc hai

A. Lý thuyết Căn bậc hai

1. Căn bậc hai

• Căn bậc hai của số thực không âm a là số thực x sao cho x² = a.

Ví dụ: Căn bậc hai của 16 là 4 và −4 vì 4² = (−4)² = 16.

Tính chất:

• $\sqrt{a^{2}} = |a|$ với mọi số thực a.

Ví dụ: Ta có $\sqrt{81} = 9$ nên căn bậc hai của 81 là 9 và −9.

Nhận xét:

• Số âm không có căn bậc hai.

• Số 0 có một căn bậc hai duy nhất là 0.

• Số dương a có đúng hai căn bậc hai đối nhau là $\sqrt{a}$ (căn bậc hai số học của a) và $- \sqrt{a}$ .

2. Căn bậc hai số học

Số dương a có đúng hai căn bậc hai là: $\sqrt{a}$ và $- \sqrt{a}$

Với số dương $a$ , số $\sqrt{a}$ được gọi là căn bậc hai số học của $a$ .

Số $0$ cũng được gọi là căn bậc hai số học của $0$ .

+) $\sqrt{a} = x \Leftrightarrow {\begin{cases} x \geq 0 \\ x^{2} = a \end{cases}$

+) So sánh hai căn bậc hai số học:

Với hai số $a, b$ không âm ta có $a < b \Leftrightarrow \sqrt{a} < \sqrt{b}$ .

- Căn bậc hai của các số từ 0 đến 10

n	$\sqrt{n}$
0	0
1	1
2	1,414
3	1,732
4	2
5	2,236
6	2,449
7	2,646
8	2,828
9	3
10	3,162

Căn bậc hai của số âm và số phức

- Căn bậc hai của một số âm là số chỉ tồn tại trong một tập hợp bao quát hơn gọi là tập số phức .

- Bình phương của mọi số dương và âm đều là số dương và bình phương của 0 là 0. Bởi vậy không có số âm nào có căn bậc hai thực.

- Bình phương của mọi số dương và âm đều là số dương, và bình phương của 0 là 0. Bởi vậy, không có sô âm nào có căn bậc hai thực. Tuy nhiên ta có thể tiếp tục với ột tập hợp bao quát hơn gọi là số phức, trong đó chứa căn bậc hai của số âm. Một số mới kí hiệu là i, gọi là đơn vị ảo sao cho $i^{2}=-1$ . Từ đây ta có thể tưởng tượng i là căn bậc hai của -1.Tổng quát: nếu x là một số không âm bất kì thì căn bậc hai chính là $\sqrt{-x}=i\sqrt{x}$ . Dối với mọi số phức z khác không tồn tại số w sao cho w $^{2}$ = z.

3. Căn thức bậc hai

Với $A$ là một biểu thức đại số, người ta gọi $\sqrt{A}$ là căn thức bậc hai của $A$ . Khi đó, $A$ được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.

$\sqrt{A}$ xác định hay có nghĩa khi $A$ lấy giá trị không âm.

Chú ý.:

Với $a \geq 0,$ ta có:

+ Nếu $x = \sqrt{a}$ thì ${\begin{cases} x \geq 0 \\ x^{2} = a \end{cases}$

+ Nếu ${\begin{cases} x \geq 0 \\ x^{2} = a \end{cases}$ thì $x = \sqrt{a} .$

Ta viết $x = \sqrt{a} \Leftrightarrow {\begin{cases} x \geq 0 \\ x^{2} = a \end{cases}$

4. So sánh các căn bậc hai số học

ĐỊNH LÍ:

Với hai số $a; b$ không âm ta có $a < b \Leftrightarrow \sqrt{a} < \sqrt{b}$

Ví dụ: So sánh 3 và $\sqrt{7}$

Ta có: $3 = \sqrt{9}$ mà $9 > 7$ suy ra $\sqrt{9} > \sqrt{7}$ hay $3 > \sqrt{7}$

Hằng đẳng thức $\sqrt{A^{2}} = | A |$

Với mọi số $a$ , ta có $\sqrt{a^{2}} = | a |$ .

* Một cách tổng quát, với $A$ là một biểu thức ta có

$\sqrt{A^{2}} = | A |$ nghĩa là

$\sqrt{A^{2}} = A$ nếu $A \geq 0$ và $\sqrt{A^{2}} = - A$ nếu $A < 0$ .

B. Một số dạng toán thường gặp

Dạng 1: Tìm căn bậc hai số học và so sánh hai căn bậc hai

Phương pháp:

Sử dụng kiến thức với hai số $a, b$ không âm ta có $a < b \Leftrightarrow \sqrt{a} < \sqrt{b}$ .

Dạng 2: Tính giá trị của biểu thức chứa căn bậc hai

Phương pháp:

Sử dụng hằng đẳng thức $\sqrt{A^{2}} = | A | = {\begin{cases} A k h i A \geq 0 \\ - A k h i A < 0 \end{cases}$

Dạng 3: Rút gọn biểu thức chứa căn bậc hai

Phương pháp:

- Đưa các biểu thức dưới dấu căn về hằng đẳng thức (thông thường là ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ , ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ )

- Sử dụng hằng đẳng thức $\sqrt{A^{2}} = | A | = {\begin{cases} A k h i A \geq 0 \\ - A k h i A < 0 \end{cases}$

Dạng 4: Tìm điều kiện để biểu thức chứa căn bậc hai có nghĩa

Phương pháp:

Sử dụng kiến thức biểu thức $\sqrt{A}$ có nghĩa khi và chỉ khi $A \geq 0.$

Dạng 5: Giải phương trình chứa căn bậc hai

Phương pháp:

Ta chú ý một số phép biến đổi tương đương liên quan đến căn thức bậc hai sau đây:

$\sqrt{A} = B \Leftrightarrow {\begin{cases} B \geq 0 \\ A = B^{2} \end{cases}$ ;

$\sqrt{A^{2}} = B \Leftrightarrow | A | = B$

$\sqrt{A} = \sqrt{B} \Leftrightarrow {\begin{cases} A \geq 0 (B \geq 0) \\ A = B \end{cases}$ ;

$\sqrt{A^{2}} = \sqrt{B^{2}} \Leftrightarrow | A | = | B | \Leftrightarrow A = \pm B$

B. Bài tập căn bậc hai

1. Bài tập trắc nghiệm

Câu 1: Cho số thực a> 0. Số nào sau đây là căn bậc hai số học của a?

A. $\sqrt{a}$

B. $-\sqrt{a}$

C. $\sqrt{2a}$

D. $2\sqrt{a}$

Câu 2: Cho sô thực a>0. Căn bậc hai số học của a là x khi và chỉ khi:

A. $x=\sqrt{a}$

B. $\sqrt{x}=a$

C. $a^{2}=x$ và x>=0

D. $x^{2=a}$ và x>=0

Câu 3: Số nào sau đây là căn bậc hai số học của số a =0.36

A. -0.6

B. 0.6

C. 0.9

D. -0.18

Câu 4: Số nào sau đây là căn bậc hai số học của số a =2.25

A. -1.5 và 1.5

B. 1.25

C. 1.5

D. -1.5

Câu 5: Khẳng định nào sau đây là sai:

A. $\sqrt{A^{2}}=A$ khi A>=0

B. $\sqrt{A^{2}}=-A$ khi A<0

C. $\sqrt{A}=\sqrt{B}$ $\Leftrightarrow 0<=A<B$

D. $A>B\Leftrightarrow 0<=A<B$

Câu 6: So sánh hai số 5 và $\sqrt{50}-2$

A. $5>\sqrt{50}-2$

B. $5=\sqrt{50}-2$

C. $5<\sqrt{50}-2$

D. chưa đủ điều kiện để so sánh

Câu 9: Biểu thức $\sqrt{x-3}$ có nghĩa khi

A. x < 3

B.x < 0

C. x>= 0

D. x>=3

Câu 10: Biểu thức $\sqrt{10+100x}$ có nghĩa khí

A. x<10

B, x>=1/10

C.x>=-1/10

D. x>= 10

Câu 11: Tìm các số x không âm thỏa mãn căn x >=3

A. $\sqrt{x}>=9$

B. x< 9

C.x > 9

D. x < = 9

Câu 12: Căn bậc hai số học của 9 là

A. 3

B. -3

C.81

D. cả A và B

Câu 13: Câu nào sau đây đúng nhất?

Căn bậc hai số học của 16 bằng

A. 4

B. -4

C. 4 hoặc -4

D. 4 và -4

Câu 14: trong một căn thức:

A.dưới một dấu căn có thể chứa số hoặc chỉ chứa chữ, không thể đồng thời chứa cả hai loại

B. dưới một dấu căn chỉ có thể chứa các căn thức khác

C. dưới một dấu căn chỉ có thể chứa một phân số

D. cả ba câu trên đều sai

E. dưới một dấu căn có thể chứa số, chứa chữ, hoặc có thể chứa cả những dấu căn khác, cùng với các phép tính số học.

Câu 15: Cho số a< . Câu nào sau đây là câu sai?

A. căn bậc hai của a là căn bậc hai số học của số không âm a

B. số a có căn bbậchai lớn hơn 0 và nhỏ hơn 0

C. một trong hai câu A và B là câu sai

D. có ít nhất một trong hai câu A và B là câu đúng

Câu 16: Khẳng định nào sau đây là đúng?

A. căn bậc hai của 121 là 11

B. căn bậc hai của 144 là 12

C. căn bậc hai của 169 là 13 và -13

D. căn bậc hai của 144 là -12

Câu 17: Giải phương trình căn bậc hai của x = -2

A. phương trình có nghiệm bằng - 4

B. phương trình có nghiệm bằng 4

C. phương trình có nghiệm là 4 và -4

D. phương trình vô

Câu 18: Chọn câu đúng:

A. số dương chỉ có một căn bậc hai

B. số dương có hai căn bậc hai là hai số đối nhau

C. số dương không có căn bậc hai

D. số dương có hai căn bậc hai là hai số cùng dấu

Câu 19: Chọn câu đúng

A. số dương a có căn bậc hai là $\sqrt{a}$

B. số dương a có căn bậc hai là $-\sqrt{a}$

C. số dương a có hai căn bậc hai là $\sqrt{a}$ và $-\sqrt{a}$

D. số dương không có căn bậc hai

Câu 20: Một bạn học sinh đã làm như sau:

1. chọn kết luận đúng

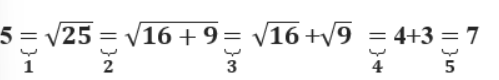
Căn bậc hai là gì? Căn bậc hai số học là gì? Căn bậc hai số học của 9 là?

A. bạn đã làm đúng

B. bạn đã làm sai từ bước 1

C. bạn đã làm sai từ bước 2

D. bạn đã làm sai từ bước 3

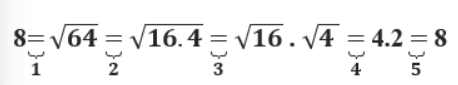
2. Căn bậc hai là gì? Căn bậc hai số học là gì? Căn bậc hai số học của 9 là?

A, bạn đã làm đúng

B. bạn đã làm sai từ bước 1

C. bạn đã làm sai từ bước 2

D. bạn đã làm sai từ bước 3

2. Bài tập vận dụng

Bài 1. Tìm căn bậc hai của mỗi số sau (làm tròn đến chữ số thập phân thứ hai):

a) 0,25;

b) $\frac{16}{81} .$

Hướng dẫn giải

a) Ta có $0, 25 = \frac{1}{4}$ mà $\sqrt{\frac{1}{4}} = \frac{1}{2} = 0, 5$ nên 0,25 có hai căn bậc hai là 0,5 và −0,5.

b) Ta có $\sqrt{\frac{16}{81}} = \frac{\sqrt{16}}{\sqrt{81}} = \frac{4}{9} \approx 0, 44$ nên $\frac{16}{81}$ có hai căn bậc hai là 0,44 và −0,44.

Bài 2. Tìm điều kiện xác định của $\sqrt{2 x - 9}$ và tính giá trị của căn thức tại x = 5.

Hướng dẫn giải

Xét căn thức $\sqrt{2 x - 9} :$

Điều kiện xác định của căn thức là 2x – 9 ≥ 0 hay $x \geq \frac{9}{2} .$

Tại x = 5 (thỏa mãn điều kiện xác định) căn thức có giá trị là $\sqrt{2.5 - 9} = 1.$

Bài 3. Rút gon các biểu thức sau:

a) $\sqrt{{(3 + \sqrt{4})}^{2}};$

b) $\sqrt{x^{2} - 6 x + 9}$ với x < 3.

Hướng dẫn giải

a) Áp dụng hằng đẳng thức $\sqrt{A^{2}} = |A|,$ ta có $\sqrt{{(3 + \sqrt{4})}^{2}} = |3 + \sqrt{4}| .$

Vì $3 + \sqrt{4} > 0$ suy ra $|3 + \sqrt{4}| = 3 + \sqrt{4} = 3 + 2 = 5$ ∀ x.

b) Áp dụng hằng đẳng thức bình phương của một hiệu và hằng đẳng thức $\sqrt{A^{2}} = |A|,$ ta có $\sqrt{x^{2} - 6 x + 9} = \sqrt{{(x - 3)}^{2}} = |x - 3| .$