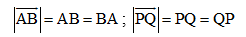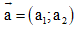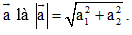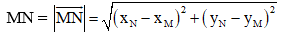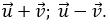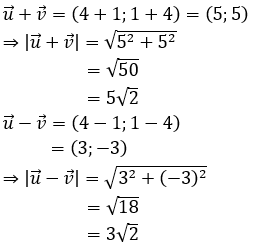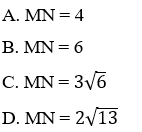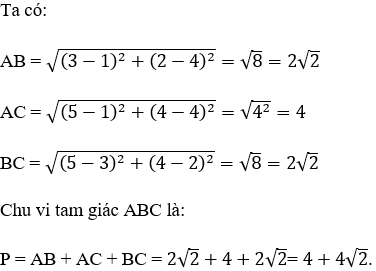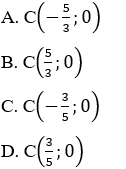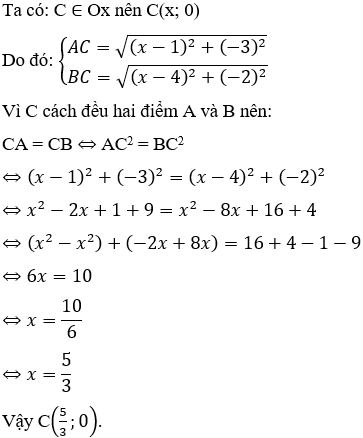Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Cách tính Độ dài vecto và bài tập ví dụ, tài liệu gồm phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Cách tính Độ dài vecto và bài tập ví dụ
1. Độ dài vecto
- Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto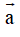 
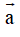
được ký hiệu là ||.
Do đó đối với các vectơ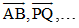 
ta có:
- Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.
- Trong hệ tọa độ: Cho 
Độ dài vectơ 
Khoảng cách giữa hai điểm trong hệ tọa độ
Áp dụng công thức sau
Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm M(xM;yM) và N(xN;yN) là
2. Phương pháp giải
- Biến đổi vectơ tổng, vectơ hiệu thành một vectơ duy nhất.
- Tính độ dài của vectơ đó.
- Từ đó suy ra độ dài của vectơ tổng, vectơ hiệu.
3. Bài tập vận dụng
Bài 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ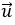 
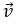
=(4;1) và 
=(1;4). Tính độ dài vectơ 
Hướng dẫn giải:
Ta có:
Bài 2: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).
Hướng dẫn giải:
Đáp án D
Bài 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.
Hướng dẫn giải:
Đáp án B
Bài 4: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?
A. Tứ giác ABCD là hình bình hành
B. Tứ giác ABCD là hình thoi
C. Tứ giác ABCD là hình thang cân
D. Tứ giác ABCD không nội tiếp được đường tròn
Hướng dẫn giải:
Đáp án C
Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).
Bài 5: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B.
Hướng dẫn giải:
Đáp án B
Đáp án B
Bài 6: Cho tam giác đều cạnh a. Khi đó bằng:
A. B.
C. D. Một đáp án khác.
Hướng dẫn giải:
Chọn A
|
Gọi H là trung điểm của Suy ra Ta lại có . |
 |
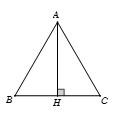Bài 7: Cho tam giác vuông cân tại A có . Tính
A. B.
C. D.
Hướng dẫn giải:
|
Chọn A. Gọi D là điểm thỏa mãn tứ giác là hình vuông. |
 |
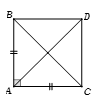Bài 8: Cho tam giác ABC vuông cân đỉnh C, . Tính độ dài của
A. B.
C. D.
Hướng dẫn giải:
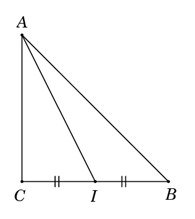
Chọn A.
Ta có
Gọi I là trung điểm
Khi đó
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
