Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Đạo hàm của hàm số y = cos2x, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Đạo hàm, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Đạo hàm của hàm số y = cos2x

A. Giải bài toán Đạo hàm của hàm số y = Cos2x

Phương pháp giải: (cos u)^' = - u . Sin u

Lời giải:

          y' = - 2 . Sin2x

B. Một số công thức tính đạo hàm

1. Đạo hàm của hàm số thường gặp:

⦁ (xⁿ)’ = nx^{n – 1};

⦁ ${\left(\sqrt{x}\right)}^{\text{'}}=\frac{1}{2\sqrt{x}}$với x > 0.

2. Đạo hàm của hàm số lượng giác:

(sinx)’ = cosx;

(cosx)’ = –sinx;

${\left(\mathrm{tanx}\right)}^{\text{'}}=\frac{1}{{\cos }^{2}x};$

${\left(\mathrm{cotx}\right)}^{\text{'}}=-\frac{1}{{\sin }^{2}x}.$

3. Đạo hàm của hàm số mũ và hàm số lôgarit:

(e^x)’ = e^x;

(a^x) = a^x.lna.

${\left(\mathrm{lnx}\right)}^{\text{'}}=\frac{1}{x};$

$\left({\log }_{a}x\right)=\frac{1}{\mathrm{xlna}}.$

4.  Đạo hàm của tổng, hiệu, tích, thương:

Giả sử các hàm số u = u(x), v = v(x) có đạo hàm trên khoảng (a; b). Khi đó:

(u + v)’ = u’ + v’;

(u – v)’ = u’ – v’;

(uv)’ = u’v + uv’;

${\left(\frac{u}{v}\right)}^{\text{'}}=\frac{u^{\text{'}}v-{\mathrm{uv}}^{\text{'}}}{v^2}\left(v=v\left(x\right)\ne 0\right)$

(ku)’ = ku’ (k là hằng số);

${\left(\frac{1}{v}\right)}^{\text{'}}=-\frac{v^{\text{'}}}{v^2}\left(v\ne 0\right).$

C. Một số bài tập về đạo hàm

Ví dụ minh họa

Ví dụ 1. Tính đạo hàm của hàm số sau:

a) f(x) = 3x² – 5x;

b) f(x) = (1 + 2x)(x – 1);

c) $f\left(x\right)=\frac{2x-1}{x^2};$

d) $f\left(x\right)=\frac{1}{\sqrt{x}}.$

Hướng dẫn giải:

a) Xét f(x) = 3x² – 5x.

Khi đó, f’(x) = (3x²)’ – (5x)’ = 6x – 5.

b) Xét f(x) = (1 + 2x)(x – 1)

Khi đó,

f’(x) = (1 + 2x)’(x – 1) + (1 + 2x)(x – 1)’

= 2(x – 1) + (1 + 2x).1

= 2x – 2 + 1 + 2x

= 4x – 1.

c) Xét $f\left(x\right)=\frac{2x-1}{x^2}.$

Khi đó với x ≠ 0, ta có:

$f^{\text{'}}\left(x\right)=\frac{{\left(2x-1\right)}^{\text{'}}{x}^2-\left(2x-1\right){\left(x^2\right)}^{\text{'}}}{{\left(x^2\right)}^2}$

$=\frac{2\cdot x^2-\left(2x-1\right)\cdot 2x}{x^4}=\frac{2x^2-4x^2+2x}{x^4}$

$=\frac{-2x^2+2x}{x^4}=\frac{-2x+2}{x^3}.$

d) Xét $f\left(x\right)=\frac{1}{\sqrt{x}}$ với x > 0.

Khi đó, $f^{\text{'}}\left(x\right)=-\frac{{\left(\sqrt{x}\right)}^{\text{'}}}{{\left(\sqrt{x}\right)}^2}=-\frac{1}{2x\sqrt{x}}$.

Ví dụ 2. Tính đạo hàm của các hàm số sau:

a) $y=\mathrm{sinx}-\frac{1}{2}\mathrm{cosx}.$

b) $y=\mathrm{tanx}-\frac{1}{\pi }\mathrm{cotx}.$

c) $y=\frac{\mathrm{sinx}}{\mathrm{sinxcosx}}.$

Hướng dẫn giải:

a) Ta có $y^{\text{'}}={\left(\mathrm{sinx}\right)}^{\text{'}}-\frac{1}{2}\left(\mathrm{cosx}\right)\text{'}=\mathrm{cosx}+\frac{1}{2}\mathrm{sinx}.$

b) Ta có $y^{\text{'}}={\left(\mathrm{tanx}\right)}^{\text{'}}-\frac{1}{\pi }{\left(\mathrm{cotx}\right)}^{\text{'}}=\frac{1}{{\cos }^{2}x}+\frac{1}{{\mathrm{\pi sin}}^{2}x}.$

c) Ta có $y^{\text{'}}=\frac{{\left(\mathrm{sinx}\right)}^{\text{'}}\mathrm{sinxcosx}-\mathrm{sinx}\cdot {\left(\mathrm{sinxcosx}\right)}^{\text{'}}}{{\left(\mathrm{sinxcosx}\right)}^2}$

$=\frac{\mathrm{cosxsinxcosx}-\mathrm{sinx}\cdot \left[{\left(\mathrm{sinx}\right)}^{\text{'}}\mathrm{cosx}+\mathrm{sinx}{\left(\mathrm{cosx}\right)}^{\text{'}}\right]}{{\left(\mathrm{sinxcosx}\right)}^2}$

$=\frac{{\mathrm{sinxcos}}^2\mathrm{x}-\mathrm{sinx}\cdot \left[{\cos }^2\mathrm{x}-{\sin }^2\mathrm{x}\right]}{{\sin }^2{\mathrm{xcos}}^2\mathrm{x}}$

$=\frac{{\cos }^{2}x-{\cos }^{2}x+{\sin }^{2}x}{{\mathrm{sinxcos}}^{2}x}=\frac{{\sin }^{2}x}{{\mathrm{sinxcos}}^{2}x}=\frac{\mathrm{sinx}}{{\cos }^{2}x}.$

Ví dụ 3. Tính đạo hàm của các hàm số sau tại điểm x₀ = 1:

a) y = 2^x;

b) y = lnx.

Hướng dẫn giải:

a) Ta có: y’ = 2^x.ln2.

Khi đó đạo hàm của hàm số y = 2^x tại điểm x₀ = 1 là: 2¹.ln2 = 2ln2.

b) Ta có: $y^{\text{'}}=\frac{1}{x}.$

Khi đó đạo hàm của hàm số y = lnx tại điểm x₀ = 1 là: $\frac{1}{1}=1.$

Ví dụ 4. Cho hàm số y = x³ + 2x² – 5x + 4.

a) Viết phương trình tiếp tuyến của đồ thị hàm số tại hoành độ x₀ = – 2;

b) Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến bằng – 6.

Hướng dẫn giải:

Hàm số y = x³ + 2x² – 5x + 4.

Ta có: y’(x) = 3x² + 4x – 5.

a) Với x₀ = –2 thì y₀ = (–2)³ + 2(–2)² – 5(–2) + 4 = 14.

Do đó, y’(–2) = 3(–2)² + 4(–2) – 5 = –1.

Phương trình tiếp tuyến của đồ thị hàm số tại hoành độ x₀ = –2 là:

y – 14 = – 1[x – (– 2)] hay y = – x + 12.

b) Gọi A(x₀; y₀) là tiếp điểm thuộc đồ thị hàm số y = x³ + 2x² – 5x + 4.

Do hệ số góc tiếp tuyến của đồ thị hàm số bằng – 6 nên

y’(x₀) = – 6 ⇔ 3x₀² + 4x₀ – 5 = – 6 ⇔ x₀ = – 1 hoặc $x_0=\frac{-1}{3}$

Với x₀ = – 1 thì y₀ = 10, phương trình tiếp tuyến cần tìm là y – 10 = – 6(x + 1) hay y = –6x + 4.

Với $x_0=\frac{-1}{3}$ thì $y_0=\frac{158}{27}$, phương trình tiếp tuyến cần tìm là$y-\frac{158}{27}=-6\left(x+\frac{1}{3}\right)$hay $y=-6x+\frac{104}{27}$

Bài tập trắc nghiệm

Bài 1: Đạo hàm của hàm số y = (2x⁴ - 3x² - 5x)(x² - 7x) bằng biểu thức nào dưới đây?

A. (8x³ - 6x - 5)(2x - 7)

B. (8x³ - 6x - 5)(x² - 7x) - (2x⁴ - 3x² - 5x)(2x - 7)

C. (8x³ - 6x - 5)(x² - 7x)+(2x⁴ - 3x² - 5x)(2x - 7)

D. (8x³ - 6x - 5) + (2x - 7)

Lời giải:

Đáp án: C

Áp dụng công thưc đạo hàm hàm hơp (uv)’= u’v + uv’ ta có:

y' = (8x³ - 6x - 5)(x² - 7x) + (2x⁴ - 3x² - 5x)(2x - 7)

Chọn đáp án là C

Bài 2: Đạo hàm của hàm số 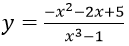 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: D

Áp dụng công thưc đạo hàm hàm hơp  ta có:

Chọn đáp án là D

Bài 3: Đạo hàm của hàm số 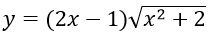 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Ta có:

Bài 4: Đạo hàm của hàm số f(t) = a³t⁴ - 2at² + 3t - 5a bằng biểu thức nào sau đây?

A. 4a³t³ - 4at + 3

B. 3a²t⁴ - 2t² - 5

C. 12a²t³ - 4at - 2

D. 4a³t³ - 4at - 5

Lời giải:

Đáp án: A

f'(t) = 4a³t³ - 4at + 3

Chọn đáp án là A

Bài 5: Đạo hàm của hàm số 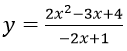 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Bài 6: Đạo hàm cuả hàm số 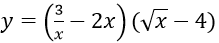 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Bài 7: Đạo hàm của hàm số 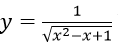 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài 8: Đạo hàm của hàm số 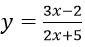 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 9: Đạo hàm của hàm số 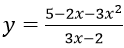 bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: C

Bài 10: Đạo hàm của hàm số:

 bằng biểu thức nào dưới đây?

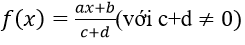
Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 11: Đạo hàm của hàm số f(x) = a³ - 3at² - 5t³(với a là hằng số) bằng biểu thức nào sau đây?

A. 3a² - 6at - 15t²

B. 3a² - 3t²

C. -6at - 15t²

D. 3a² - 3t² - 6at - 15t²

Lời giải:

Đáp án: C

f(t) = a³ - 3at² - 5t³

f'(t) = -6at - 15t²

Chọn đáp án là C

Bài 12: Đạo hàm của hàm số 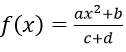 bằng biểu thức nào sau đây?

Lời giải:

Đáp án: A

Chọn đáp án là A

Bài 13: Đạo hàm của hàm số f(x) = t²x + tx² bằng biểu thức nào sau đây?

A. 2tx + x²

B. t² + 2tx

C. 2x + 2tx

D. 2tx + 2tx

Lời giải:

Đáp án: B

Biến là x (t là hằng số), do đó B đúng

Bài 14: Đạo hàm của hàm số 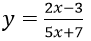 bằng biểu thức nào sau đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài 15: Đạo hàm của hàm số 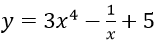 bằng biểu thức nào sau đây?

Lời giải:

Đáp án: B

Chọn đáp án là B

Bài tập tự luyện

Bài 1. Các khẳng định sau Đúng hay Sai

Bài 2.

a) Cho y = 3x³ + x⁴ – 5x. Tính y’(1);

b) Cho $y=\frac{3}{\sqrt{x}}$. Tính y’(3);

c) Cho $y=\frac{x^2+x+1}{2x+3}$. Tính y’(–1).

d) Cho y = 4^x + e^x. Tính y’(2).

e) Cho y = 2xlnx. Tính y’(3).

f) Cho y = sinx + 2cosx – 3tanx + 4cotx. Tính $y^{\text{'}}\left(\frac{\pi }{4}\right).$

Bài 3. Pháo hoa tầm thấp được bắn lên cao theo phương thẳng đứng có phương trình chuyển động h(t) = 9,8t² + 19,6t – 18, trong đó $t\ge 0$, t(s) là thời gian chuyển động và h(m) là độ cao so với mặt đất.

a) Sau bao lâu để từ khi bắn pháo hoa ở độ cao 1158m?

b) Vận tốc tức thời của pháo hoa khi ở độ cao 325m?

c) Tại thời điểm pháo hoa có vận tốc tức thời 78,4 (m/s) thì pháo hoa đang ở độ cao bao nhiêu so với mặt đất?

Bài 4. Cho hàm số y = (x³ – 2)(1 – x²).

a) Tính đạo hàm của đồ thị hàm số tại một điểm x₀ bất kì;

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x₀ = 2;

c) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ y₀ = 0.

Bài 5. Một vật rơi tự do với vận tốc ban đầu v₀ = 54 m/s (bỏ qua sức cản của không khí) sau thời gian t thì có phương trình $s\left(t\right)=\frac{1}{2}{\mathrm{gt}}^2-\left(v_0-5\right)t$, trong đó $g\approx 9,8m/s^2$ là gia tốc trọng trường. Tính vận tốc khi vật đó chạm đất