Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức lớp 9

Thuý Vân Ngày: 12-09-2024 Tổng hợp kiến thức

Tải xuống 26 21.8 K 444

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề HSG: Tìm GTLN, GTNN của biểu thức môn Toán lớp 9, tài liệu bao gồm 26 trang, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

A. Các kiến thức thường sử dụng là

+ Bất đẳng thức Côsi: “Cho hai số không âm a, b; ta có bất đẳng thức:

Dấu “=” xảy ra khi và chỉ khi a = b”.

$+ Bất đẳng thức : {(ac + bd)}^{2} \leq (a^{2} + b^{2}) . (c^{2} + d^{2}) Dấu = xảy ra \Leftrightarrow \frac{a}{c} = \frac{b}{d}$

+ $|a| + |b| \geq |a + b| D ấ u = x ả y r a k h i v à c h ỉ k h i a b \geq 0$

+ Sử dụng “bình phương” để tìm giá trị lớn nhất, giá trị nhỏ nhất.

$Nếu y = a + {[f (x)]}^{2} thì \min y = a khi f (x) = 0 Nếu y = a - {[f (x)]}^{2} thì \max y = a khi f (x) = 0$

+ Phương pháp “tìm miền giá trị” (cách 2 ví dụ 1 dạng 2).

CÁC DẠNG TOÁN VÀ CÁCH GIẢI

Dạng 1: CÁC BÀI TOÁN MÀ BIỂU THỨC CHO LÀ MỘT ĐA THỨC

Bài toán 1: Tìm GTNN của các biểu thức:

a. A = $4 x^{2} + 4 x + 11$

b. B = (x-1)(x+2)(x+3)(x+6)

c. $C = x^{2} - 2 x + y^{2} - 4 y + 7$

Giải:

a. A = $4 x^{2} + 4 x + 11 = 4 x^{2} + 4 x + 1 + 10 = {(2 x + 1)}^{2} + 10 \geq 10$

Min A = 10 khi x=-1/2

b.B = (x-1)(x+2)(x+3)(x+6) = (x-1)(x+6)(x+2)(x+3)

= (x² + 5x – 6)(x² + 5x + 6) = (x² + 5x)² – 36 -36

Min B = -36 khi x = 0 hoặc x = -5

c. $C = (x^{2} - 2 x + 1) + (y^{2} - 4 y + 4) + 2 = {(x - 1)}^{2} + {(y - 2)}^{2} + 2 \geq 2$

=> Min C=2 khi x=1; y=2

Bài toán 6: Cho 0 ≤ a, b, c ≤ 1. Tìm GTLN và GTNN của biểu thức:

P = a + b + c – ab – bc – ca.

Giải:

Ta có: P = a + b + c – ab – bc – ca

= (a – ab) + (b - bc) + (c – ca)

= a(1 – b) + b(1 – c) + c(1 – a) 0 (vì )

Dấu “=” có thể xảy ra chẳng hạn: a = b = c = 0

Vậy GTNN của P = 0

Theo giả thiết ta có: 1 – a 0; 1 – b 0; 1 – c 0;

(1-a)(1-b)(1-c) = 1 + ab + bc + ca – a – b – c – abc 0

P = a + b + c – ab – bc – ac

Dấu “=” có thể xảy ra chẳng hạn: a = 1; b = 0; c tùy ý

Vậy GTLN của P = 1.

B. Các bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức

I. Dạng 1: Đa thức có dấu giá trị tuyệt đối

Phương pháp: Có hai cách để giải bài toán này:

Cách 1: Dựa vào tính chất |x| ≥ 0. Ta biến đổi biểu thức A đã cho về dạng A ≥ a (với a là số đã biết) để suy ra giá trị nhỏ nhất của A là a hoặc biến đổi về dạng A ≤ b (với b là số đã biết) từ đó suy ra giá trị lớn nhất của A là b.

Cách 2: Dựa vào biểu thức chứa hai hạng tử là hai biểu thức trong dấu giá trị tuyệt đối. Ta sẽ sử dụng tính chất:

∀x, y ∈ $\mathbb{Q}$ ta có:

$\left | x+y \right |\leq\left | x\right | +\left | y\right |$
$\left | x-y \right |\leq\left | x\right | -\left | y\right |$

Ví dụ 1: Tìm giá trị nhỏ nhất của các biểu thức sau:

a. A = (3x - 1)² - 4|3x - 1| + 5

b. B = |x - 2| + |x - 3|

Lời giải:

a, A = (3x - 1)² - 4|3x - 1| + 5

Đặt $y = \left| {3x - 1} \right|$

$\Rightarrow A = {y^2} - 4y + 5 = {\left( {y - 2} \right)^2} + 1 \ge 1$

Do đó, min A = 1⇔ y = 2.

$\Leftrightarrow \left| {3x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 2\\3x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{3}\end{array} \right.$

b, $B = \left| {x - 2} \right| + \left| {x - 3} \right|$

$B = \left| {x - 2} \right| + \left| {x + 3} \right| \ge \left| {x - 2 + 3 - x} \right| = 1$

$\Rightarrow \min B = 1 \Leftrightarrow \left( {x - 2} \right)\left( {3 - x} \right) \ge 0 \Leftrightarrow 2 \le x \le 3$

Ví dụ 2: Tìm giá trị nhỏ nhất của C = |x² - x + 1| + |x² - x - 2|

Hướng dẫn giải

Ta có: C = |x² - x + 1| + |x² - x - 2|

≥ |x² - x + 1 + 2 + x - x²| = 3

MinC = 3 ⇔ (x² - x + 1)(2 + x - x²) ≥ 0

⇔ (x + 1)(x - 2) ≤ 0 ⇔ -1 ≤ x ≤ 2

Ví dụ 3: Tìm giá trị nhỏ nhất của T = |x - 1| + |x - 2| + |x - 3| + |x - 4|

Hướng dẫn giải

Ta có |x - 1| + |x - 4| ≥ |x - 1 + 4 - x| = 3 (1)

|x - 2| + |x - 3| ≥ |x - 2 +3 - x| = 1 (2)

Vậy T ≥ 1 + 3 = 4

Từ (1) suy ra dấu bằng xảy ra khi 1 ≤ x ≤ 4

Từ (2) suy ra dấu bằng xảy ra khi 2 ≤ x ≤ 3

Vậy T có giá trị nhỏ nhất bằng 4 khi 2 ≤ x ≤ 3

II. Dạng 2: Tam thức bậc hai

Phương pháp: Đối với dạng tam thức bậc hai ta đưa biểu thức đã cho về dạng bình phương một tổng (hoặc hiệu) cộng (hoặc trừ) đi một số tự do.

Tổng quát:

d - (a ± b)² ≤ d Ta tìm được giá trị lớn nhất
(a ± b)²± c ≥ ± c Ta tìm được giá trị nhỏ nhất

Ví dụ 1: Tìm giá trị lớn nhất của biểu thức B = 6 - 8x - x²

Lời giải

Ta có: B = 6 - 8x - x²

B = - (x² + 8x) + 6

B = - (x² + 8x + 16) + 6 + 16

B = - (x + 4)² + 22

Vì (x + 4)² ≥ 0 với mọi x

⇒ - (x + 4)²≤ 0 với mọi x

⇒ - (x + 4)²+ 22 ≤ 22 với mọi x

⇒ B ≤ 22 với mọi x

Vậy giá trị lớn nhất của biểu thức B là 22

Ví dụ 2. Tìm giá trị nhỏ nhất của biểu thức C = 4x² + 8x + 10

Lời giải

C = 4x² + 8x + 10

= (2x)² + 2 . 2x . 2 + 4 + 6

= (2x + 2)² + 6

Với mọi x ta có: (2x + 2)² ≥ 0

⇒ (2x + 2)²+ 6 ≥ 6

⇒ C ≥ 6

Do đó, giá trị nhỏ nhất của biểu thức C là 6.

Ví dụ 3:

a, Tìm giá trị nhỏ nhất của A = 2x² - 8x + 1

b, Tìm giá trị lớn nhất của B = -5x² - 4x + 1

Lời giải:

a, A = 2(x² - 4x + 4) - 7

= 2(x - 2)² - 7 ≥ -7

Vậy min A = - 7 khi và chỉ khi x = 2

b, Ta có: $B = - 5\left( {{x^2} + \frac{4}{5}x} \right) + 1$

$= - 5\left( {{x^2} - 2.x.\frac{2}{5} + \frac{4}{{25}}} \right) + \frac{9}{5}$

$= \frac{9}{5} - 5{\left( {x + \frac{2}{5}} \right)^2} \le \frac{9}{5}$

Vậy max $B = \frac{9}{5} \Leftrightarrow x = - \frac{2}{5}$

Ví dụ 4: Cho tam thức bậc hai P(x) = ax² + bx + c

a, Tìm min P nếu a > 0

b, Tìm max P nếu a < 0

Lời giải:

Ta có $P = a\left( {{x^2} + \frac{b}{a}x} \right) + c$

$= a{\left( {x + \frac{b}{{2a}}} \right)^2} + \left( {c - \frac{{{b^2}}}{{4a}}} \right)$

Đặt $k = c - \frac{{{b^2}}}{{4a}}$ . Do ${\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0$ nên:

a, Nếu a > 0 thì $a{\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0$ do đó P ≥ k ⇒ min P = k

b, Nếu a < 0 thì $a{\left( {x + \frac{b}{{2a}}} \right)^2} \le 0$ do đó P ≤ k ⇒ max P = k ⇒ $x = \frac{{ - b}}{{2a}}$

III. Dạng 3: Đa thức bậc cao

Phương pháp: Đưa đa thức về dạng tổng các bình phương.

Ví dụ 1: Tìm giá trị nhỏ nhất của các đa thức sau:

a. A = x(x - 3)(x - 4)(x - 7)

b. B = 2x² + y² - 2xy - 2x + 3

c. C = x² + xy + y² - 3x - 3

Lời giải:

a, A = x(x - 3)(x - 4)(x - 7)

= (x² - 7x)(x² - 7x + 12)

Đặt y = x² - 7x + 6 thì A = (y - 6)(y + 6) = y² - 36 ≥ - 36

$\min A = - 36 \Leftrightarrow y = 0$

$\Leftrightarrow {x^2} + 7x + 6 = 0$

$\Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 6\end{array} \right.$

b, B = 2x² + y² - 2xy - 2x + 3

= (x² - 2xy + y²) + (x² - 2x + 1) + 2

$= {\left( {x - y} \right)^2} + {\left( {x - 1} \right)^2} + 2 \ge 2$

Dấu "=" xảy ra $\Leftrightarrow \left\{ \begin{array}{l}x - y = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow x = y = 1$

c, C = x² + xy + y² - 3x - 3

= x² - 2x + y² - 2y + xy - x - y

Ta có $C + 3 = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 2y + 1} \right) + \left( {xy - x - y + 1} \right)$

$= {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + \left( {x - 1} \right)\left( {y - 1} \right)$

Đặt a = x - 1; b = y - 1 thì

$C + 3 = {a^2} + {b^2} + ab$

$= \left( {{a^2} + 2.a.\frac{b}{2} + \frac{{{b^2}}}{4}} \right) + \frac{{3{b^2}}}{4}$

$= {\left( {a + \frac{b}{2}} \right)^2} + \frac{{3{b^2}}}{4} \ge 0$

Vậy Min(C + 3) = 0 hay min C = - 3⇔ a = b = 0 ⇔ x = y = 1

C. Bài tập vận dụng

Câu 1. Tìm giá trị lớn nhất của biểu thức B = 10 - x²

A. 0

B. 10

C. -10

D. 9

Đáp án: B

Ta có: x² ≥ 0 ⇒ 10 - x² ≤ 10

Vậy min B = 10.

Câu 2. Tìm giá trị lớn nhất của biểu thức A = 4x - 2x²

A. 0

B. 1

C. 4

D. 2

Đáp án: D

Ta có: A = 4x - 2x² = - 2(x² - 2x)

= - 2(x² - 2x + 1) + 2

= - 2(x - 1)² + 2

Vì (x - 1)² ≥ 0 với mọi x

⇒ - 2(x - 1)² + 2 ≤ 2

Do đó, giá trị lớn nhất của biểu thức A là 2.

Câu 3 . Tìm giá trị lớn nhất của biểu thức C = 4x + 3 - x²

A. 7

B. 4

C. 3

D. -1

Đáp án: A

Ta có: C = 4x + 3 - x²

= - (x - 2)² + 7 ≤ 7

Vì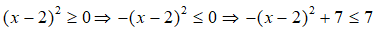

Do đó, giá trị lớn nhất của C là 7.

Câu 4. Tìm giá trị lớn nhất của biểu thức D = - x² + 6x - 11

A. - 11

B. 6

C. - 2

D. 9

Đáp án: C

D = - x² + 6x - 11 = - (x² - 6x) - 11

= - (x² - 6x + 9) + 9 - 11

= - (x - 3)² - 2

Vì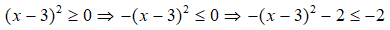

Giá trị lớn nhất của biểu thức D là – 2

Câu 5. Tìm giá trị lớn nhất của biểu thức E = 4x - x² + 1

A. 1

B. 5

C. 3

D. 6

Đáp án: B

Ta có: E = 4x - x² + 1

= - (x² - 4x) + 1

= - (x² - 4x + 4) + 4 + 1

= - (x - 2)² + 5

Vì - (x - 2)² ≤ 0 ⇒ - (x - 2)² + 5 ≤ 5

Do đó, giá trị lớn nhất của biểu thức E là 5.

Câu 6. Tìm giá trị nhỏ nhất của biểu thức A = 2x² + 8x + 11

A. 3

B. 8

C. 11

D. 9

Câu 7. Tìm giá trị nhỏ nhất của biểu thức E = x² - 2x + y² + 4y + 10

A. 1

B. 10

C. 5

D.8

Câu 8. Tìm giá trị nhỏ nhất của biểu thức D = 4x² + y² + 6y + 20

A. 20

B. 11

C. 10

D.16

Câu 9. Tìm giá trị nhỏ nhất của biểu thức G = x² + 5y² - 4xy - 8y + 28

A. 10

B. 8

C. 20

D.15

Câu 10. Tìm giá trị nhỏ nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Câu 11. Tìm giá trị nhỏ nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Lời giải: ĐKXĐ của phân thức x ≠ 1.

Ta có:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy min A = 2 khi và chỉ khi x - 2 = 0 ⇔ x =2

Câu 12. Tìm giá trị nhỏ nhất và giá trị lớn nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

a, Tìm GTNN

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy min A = -1 khi và chỉ khi x - 2 = 0 ⇔ x = 2

b, Tìm GTLN

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy max A= 4 khi và chỉ khi 2x + 1= 0⇔ 2x = -1 ⇔ x = -1/2

Câu 13. Tìm giá trị lớn nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Câu 14. Tìm giá trị nhỏ nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Câu 15. Tìm giá trị nhỏ nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Câu 16. Tìm giá trị nhỏ nhất và giá trị lớn nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

a, Tìm GTNN

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vì x² + 9 ≥ 9 , (x – 6)² ≥ 0 với mọi x

⇒ P ≥ - 1

Vậy min P = -1 ⇔ x – 6 = 0 ⇔ x = 6

Tim GTLN

b,Ta có:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy max P =4 ⇔ 2x + 3 = 0 ⇔ x = -3/2

Câu 17. Tìm giá trị nhỏ nhất và giá trị lớn nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

a, Tìm GTNN

Ta có:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy min D = -1/2 ⇔ x = -2

Tim GTLN

Ta có Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Vậy max D = 1 ⇔ x = 1

Câu 18. Tìm giá trị nhỏ nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Câu 19. Tìm giá trị lớn nhất của phân thức Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

Lời giải:

Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của phân thức cực hay, có đáp án

D. Bài tập tự luyện

Bài 1. Tìm giá trị nhỏ nhất của biểu thức: Q = $\frac{3 x^{2} + 3 x - 5}{x^{2} + x}$ .

Bài 2. Tìm giá trị lớn nhất của biểu thức: Q = $\frac{10}{5 x^{2} + 10 x + 1}$ .

Bài 3. Tìm giá trị lớn nhất của biểu thức: Q = $\frac{x^{2} + 2 x + 8}{3 x^{2} + 6 x + 12}$ .

Bài 4. Tìm giá trị nhỏ nhất của biểu thức: Q = $\frac{x^{2} + 3 x}{2 x^{2} + 6 x + 7}$ .

Bài 5. Tìm giá trị lớn nhất của biểu thức: Q = $\frac{2}{3 x^{2} + 5}$ .

Bài 6. Tìm giá trị nhỏ nhất của biểu thức:

a, $A = 2{x^2} + 2xy + {y^2} - 2x + 2y + 2$

b, $B = {x^4} - 8xy + {x^3}y + {x^2}{y^2} - x{y^3} + {y^4} + 200$

c, $C = {x^2} + xy + {y^2} - 3x - 3y$

d, $D = x\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)$

Bài 7. Tìm giá trị lớn nhất của biểu thức:

A = - x² - y² + xy + 2x + 2y

Bài 8. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

a, A = -x² + x + 1	b, B = x² + 3x + 4
c, C = x² - 11x + 30	d, D = x² - 2x + 5
e, E = 3x² - 6x + 4	f, F = -3x² - 12x - 25

Bài 9. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

A = |x - 2004| + |x - 2005|

B = |x - 2| + |x - 9| + 1945

C = -|x - 7| - |y + 13| + 1945

Bài 10. Chứng minh rằng không có giá trị x, y, z thoả mãn:

x² + 4y² + z² - 2x + 8y - 6z + 15 = 0

Tài liệu có 26 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Chuyên đề Toán toán 9

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm