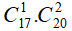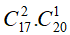Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Cách phân biệt hoán vị chỉnh hợp tổ hợp và bài tập ví dụ, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Cách phân biệt hoán vị chỉnh hợp tổ hợp và bài tập ví dụ
1. Hoán vị
Cho phần tử khác nhau (). Mỗi cách sắp thứ tự của phần tử đã cho, mà trong đó mỗi phần tử có mặt đúng một lần, được gọi là một hoán vị của phần tử đó.
Định lí
Số các hoán vị của phần tử khác nhau đã cho () được kí hiệu là và bằng:
Ví dụ:
Tính số cách xếp bạn học sinh thành một hàng dọc.
Hướng dẫn:
Mỗi cách xếp bạn học sinh thành một hàng dọc là một hoán vị của phần tử.
Vậy số cách xếp bạn học sinh thành một hàng dọc là .
2. Chỉnh hợp
Định nghĩa
Cho tập hợp gồm phần tử .
Kết quả của việc lấy phần tử khác nhau từ phần tử của tập hợp và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Chú ý
Mỗi hoán vị của n phần tử khác nhau đã cho chính là một chỉnh hợp chập của phần tử đó.
Định lí
Số chỉnh hợp chập của phần tử khác nhau đã cho được kí hiệu là và bằng
Với quy ước .
Ví dụ:
Có bao nhiêu số tự nhiên gồm chữ số khác nhau được lập thành từ các chữ số ?
Hướng dẫn:
Mỗi số tự nhiên gồm chữ số khác nhau được lập bằng cách lấy chữ số từ tập và xếp chúng theo một thứ tự nhất định.
Mỗi số như vậy được coi là một chỉnh hợp chập của phần tử.
Vậy số các số cần tìm là số.
3. Tổ hợp
Định nghĩa
Cho phần tử khác nhau (). Mỗi tập con gồm phần tử khác nhau (không phân biệt thứ tự) của tập hợp phần tử đã cho () được gọi là một tổ hợp chập của phần tử đã cho (với quy ước tổ hợp chập của n phần tử bất kỳ là tập rỗng).
Định lí
Số các tổ hợp chập của phần tử khác nhau đã cho được kí hiệu là và bằng
= , ()
Ví dụ:
Một bàn học sinh có nam và nữ. Có bao nhiêu cách chọn ra bạn để làm trực nhật?
Hướng dẫn:
Mỗi cách chọn ra bạn để làm trực nhật là một tổ hợp chập của phần tử.
Vậy số cách chọn là: (cách)
Định lí
Với mọi , ta có:
a)
b) = .
4. Cách phân biệt hoán vị chỉnh hợp tổ hợp

Mối quan hệ giữa tổ hợp, chỉnh hợp và hoán vị:
Thông qua định nghĩa, chúng ta có thể thấy tổ hợp, chỉnh hợp và hoán vị có một mối liên hệ với nhau.
Cụ thể một chỉnh hợp chập k của n được tạo thành cách thực hiện 2 bước như sau:
Bước 1: Lấy 1 tổ hợp chập k của n phần tử
Bước 2: Hoán vị k phần tử
Do đó, chúng ta có công thức liên hệ như sau:
Akn = CknPk
5. Bài tập tự luyện
Bài 1: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là
A. 24
B. 120
C. 60
D. 16
Xếp bạn Chi ngồi giữa có 1 cách.
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.
Vậy có 1.24 = 24 cách xếp.
Chọn đáp án A
Bài 2: Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
A. 345600
B. 725760
C.103680
D.518400
Số các hoán vị về màu bi khi xếp thành dãy là 3!
Số cách xếp 3 viên bi đen khác nhau thành dãy là 3!
Số cách xếp 4 viên bi đỏ khác nhau thành dãy là 4!
Số cách xếp 5 viên bi xanh khác nhau thành dãy là 5!
⇒ Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là 3!. 3!. 4!. 5! = 103680 cách.
Chọn đáp án C
Bài 3: Có bao nhiêu cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài?
A.15
B. 720
C. 30
D. 360
Số cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài là một chỉnh hợp chập 4 của 6 phần tử.
Suy ra có 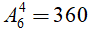
Chọn đáp án D
Bài 4: Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ thì có bao nhiêu cách chọn?
A. 210
B. 200
C. 180
D. 150
Số cách chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử.
Vậy có 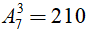
Chọn đáp án A
Bài 5: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh để tham gia vệ sinh công cộng toàn trường, hỏi có bao nhiêu cách chọn như trên?
A.9880
B. 59280
C. 2300
D. 455
Nhóm học sinh 3 người được chọn (không phân biệt nam, nữ - công việc) là một tổ hợp chập 3 của 40 (học sinh).
Vì vậy, số cách chọn nhóm học sinh là
Chọn đáp án A
Bài 6: Có bao nhiêu cách cắm 3 bông hoa giống nhau vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông)?
A. 10
B. 30
C. 6
D. 60
Cắm 3 bông hoa giống nhau, mỗi bông vào 1 lọ nên ta sẽ lấy 3 lọ bất kỳ trong 5 lọ khác nhau để cắm bông.
Vậy số cách cắm bông chính là một tổ hợp chập 3 của 5 phần tử (lọ hoa).
Như vậy, ta có 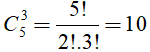
Chọn đáp án A
Bài 7: Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?
A. 15
B. 20
C. 60
D. Một số khác.
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có 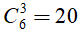
Chọn đáp án B
Bài 8: Một tổ có 4 học sinh nam và 5 học sinh nữ
a) Hỏi có bao nhiêu cách xếp học sinh trong tổ thành một hàng dọc?
A. 4!.5!
B. 4!+5!
C. 9!
D.
b) Hỏi có bao nhiêu cách xếp học sinh trong tổ thành hàng dọc sao cho học sinh nam và nữ đúng xen kẽ nhau?
A. 4!.5!
B. 4!+5!
C. 9!
D. .
- Mỗi cách xếp có 4 + 5 = 9 học sinh thành hàng dọc là một hoán vị của 9 học sinh đó. Vậy có tất cả 9! cách xếp. Chọn đáp án là C
Nhận xét: học sinh có thể nhầm lẫn xếp nam và nữ riêng nên cho kết quả 4!.5! (phương án A); hoặc vừa xếp nam và nữ riêng và sử dụng quy tắc cộng để cho kết quả 4!+5! (phương án B); hoặc chọn 4 học sinh nam trong 9 học sinh và 5 học sinh nữ trong 9 học sinh để cho kết quả ( phương án D)
b) Do số học sinh nữ nhiều hơn số học sinh nam là 1 bạn nên để nam, nữ đứng xen kẽ thì nữ đứng trước.
- Nếu đánh số theo hàng dọc từ 1 đến 9 thì cần xếp 5 học nữ vào 5 vị trí lẻ nên có 5!cách xếp; và xếp 4 học sinh nam vào 4 vị trí chẵn nên có 4!cách xếp. Theo quy tắc nhân ta có, ta có 4!.5! Cách xếp 9 học sinh thành hàng dọc xen kẽ nam nữ.
Bài 9:
a) Từ tập A = {1; 2; 3; 4; 5; 6; 7; 8; 9}, lập được bao nhiêu số có bốn chữ số khác nhau?
A. 4!
B.
C. 9
D.
b) Có bao nhiêu số có bốn chữ số khác nhau?
A. 4!
B.
C.
D. Một đáp án khác
a) Mỗi số tự nhiên có bốn chữ số khác nhau được tạo ra từ các chữ số của tập A là một chỉnh hợp chập 4 của 9 phần tử.
Vậy có số cần tìm. Chọn đáp án B
Nhận xét: học sinh có thể nhầm coi mỗi số có bốn chữ số là một hoán vị của 4 phần tử nên chọn kết quả là 4! (phương án A); hoặc là một tổ hợp tập 4 của 9 phần tử nên chọn kết quả (phương án D); hoặc suy luận có 9 cách chọn chữ số hàng nghìn và có cách chọn 3 chữ số còn lại nên có kết quả 9 (phương án C)
b) Gọi số có bốn chữ số khác nhau là
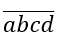
Do a ∈ {1,2,3,4,5,6,7,8,9} nên có 9 cách chọn a.
Ứng với mỗi cách chọn a, còn 10 - 1 = 9 chữ số để viết
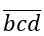
(b, c, d có thể bằng 0), mỗi cách viết
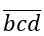
là một chỉnh hợp chập 3 của 9 chữ số, nên có số
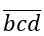
Theo quy tắc nhân, có 9 số cần tìm. Chọn đáp án là B.
Bài 10: Trong mặt phẳng có 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng
a) Số tam giác mà các đỉnh của nó thuộc tập hợp các điểm đã cho là:
A.
B.
C. 6
D.
b) Số vecto có điểm đầu và điểm cuối thuộc tập điểm đã cho là:
A.
B.
C. 6
D.
- Chọn 3 điểm trong 18 điểm đã cho làm 3 đỉnh của một tam giác. Mỗi tam giác là một tổ hợp chập 3 của 18. Vì vậy số tam giác là (chọn phương án B)
Nhận xét: học sinh có thể nhầm cho rằng mỗi tam giác là một chỉnh hợp chập 3 của 18, nên số tam giác là (phương án A); hoặc suy luận một tam giác có 3 đỉnh nên 18 điểm cho ta = 6 tam giác (phương án C); hoặc suy luận 18 điểm có 18! cách và mỗi tam giác có 3 đỉnh nên số tam giác là cách (phương án D)
- Do
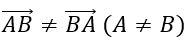
Nên mỗi vecto là một chỉnh hợp chập hai của 18.
Vì vậy, số vecto là
Chọn đáp án A
Bài 11: Có 5 bì thư khác nhau và có 8 con tem khác nhau. Chọn từ đó ra 3 bì thư và 3 con tem sau đó dán 3 con tem lên 3 bì thư đã chọn. Biết rằng một bì thư chỉ dán 1 con tem. Hỏi có bao nhiêu cách dán?
Có 5 bì thư khác nhau, chọn 3 bì thư có cách chọn
Có 8 tem khác nhau, chọn 3 con tem thì có cách chọn
Dán 3 con tem lên 3 bì thư thì có 3!cách dán khác nhau. Theo quy tắc nhân ta có 3! cách dán 3 con tem lên 3 bì thư
Nhận xét: học sinh có thể nhầm lẫn: số cách chọn 3 bì thư là , số cách chọn 3 con tem là hoặc không tính cách dán 3 con tem lên 3 bì thư dẫn đến có thể chọn các phương án A, B và C.
Bài 12: Giải phương trình Ax3+=14x (x là ẩn số)
Điều kiện x ∈ N và x ≥ 3, ta có:
Bài 13: Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai màu.
Lời giải:
Các viên bi lấy ra có đủ cả 2 màu nên ta có các trường hợp:
Cách 2. Dùng phần bù. Số cách chọn 4 viên bi tùy ý từ 11 viên bi là: 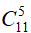
Số cách chọn 4 viên bi màu trắng là: 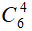
Số cách chọn 4 viên bi là màu xanh là: 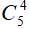
Vậy có 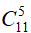
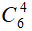
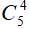
Bài 14: Từ 20 người cần chọn ra một đoàn đại biểu gồm 1 trưởng đoàn, 1 phó đoàn, 1 thư kí và 3 ủy viên. Hỏi có bao nhiêu cách chọn đoàn đại biểu ?
Lời giải:
Bài 15: Một nhóm đoàn viên thanh niên tình nguyện về sinh hoạt tại một xã nông thôn gồm có 21 đoàn viên nam và 15 đoàn viên nữ. Hỏi có bao nhiêu cách phân chia 3 nhóm về 3 ấp để hoạt động sao cho mỗi ấp có 7 đoàn viên nam và 5 đoàn viên nữ?
Lời giải:
Nhóm thứ 1: chọn 7 nam từ 21 bạn nam, chọn 5 nữ từ 15 bạn nữ nên số cách chọn nhóm thứ nhất là: 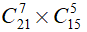
Nhóm thứ 2: chọn 7 nam từ 14 bạn nam còn lại, chọn 5 nữ từ 10 bạn nữ còn lại nên số cách chọn nhóm thứ hai là: 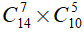
Số cách chọn nhóm thứ ba là: 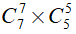
Vậy có cách chia nhóm.
Bài 16: Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh trong số học sinh giỏi đó sao cho mỗi khối có ít nhất 1 học sinh?
Lời giải:
Số cách chọn 6 học sinh bất kì trong 12 học sinh là: 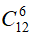
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 10 ( hay 6 học sinh từ khối 11 và 12) là: 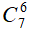
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 11 (hay 6 học sinh từ khối 10 và 12) là: 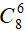
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 12 (hay 6 học sinh từ khối 10 và 11) là: 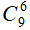
Vậy có 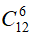
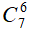
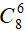
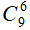
Bài 17: Một hộp bi có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Hỏi có bao nhiêu cách lấy ra 4 viên bi trong đó số viên bi đỏ lớn hơn số viên bi vàng.
Tổng số bi lấy ra có 4 viên mà bi đỏ nhiều hơn bi vàng nên có 2 trường hợp xảy ra:
TH1: Không có bi vàng, khi đó số bi đỏ phải từ 1 viên trở lên.
Số cách lấy 4 viên bi bất kì trong tổng số 9 viên bi (gồm 5 đỏ và 4 xanh) là: 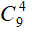
Số cách lấy 4 viên bi xanh ( khi đó bi đỏ không được lấy ra) là: 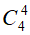
Số cách lấy thỏa mãn trong trường hợp này là: 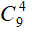
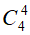
TH2: Có 1 viên bi vàng, khi đó số bi đỏ phải từ 2 viên trở lên.
Số cách lấy 1 viên bi vàng: 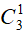
Số cách lấy 3 viên bi còn lại trong đó có 2 bi đỏ và 1 bi xanh là: 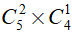
Số cách lấy 3 viên bi còn lại đều là bi đỏ là: 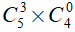
Số cách lấy thỏa mãn trong trường hợp này là:
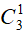
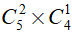
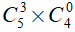
Vậy có 125 + 150 = 275 cách lấy thỏa mãn yêu cầu bài toán.
Bài 18: Tìm giá trị n ∈ N thỏa mãn 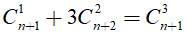
Lời giải:
Bài 19: Cho 10 điểm phân biệt A1, A2, ..., A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
Lời giải:
Số cách lấy 3 điểm từ 10 điểm phân biệt là 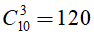
Số cách lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 là 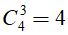
Khi lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 thì sẽ không tạo thành tam giác.
Như vậy, số tam giác tạo thành : 120 - 4 = 116 tam giác.
Bài 20: Cho hai đường thẳng song song d1 và d2. Trên d1 lấy 17 điểm phân biệt, trên d2 lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
Lời giải:
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d1 và 2 điểm thuộc d2: có 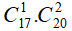
TH2. Chọn 2 điểm thuộc d1 và 1 điểm thuộc d2: có 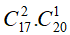
Như vậy, ta có