Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Tích phân Toán lớp 12, tài liệu bao gồm 59 trang, tuyển chọn 117 bài tập Tích phân đầy đủ lý thuyết, phương pháp giải chi tiết và lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Tích phân là gì? Công thức tính và bài tập vận dụng
A. Lý thuyết cơ bản về tích phân
1. Khái niệm và tính chất
a. Định nghĩa
Cho hàm số liên tục trên đoạn . Giả sử là một nguyên hàm của hàm số trên đoạn , hiệu số được gọi là tích phân từ đến (hay tích phân xác định trên đoạn của hàm số .
Kí hiệu là :
Vậy ta có :
Chú ý : Trong trường hợp a = b, ta định nghĩa:
Trường hợp a>b, ta định nghĩa:
Tích phân không phụ thuộc vào chữ dùng làm biến số trong dấu tích phân, tức là :
(vì đều bằng )
b. Tính chất của tích phân
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :
2. Phương pháp tính tích phân
a. Phương pháp đổi biến số
Định lí. Cho hàm số liên tục trên . Giả sử hàm số có đạo hàm liên tục trên đoạn sao cho và . Khi đó:
Chú ý. Có thể dử dụng phép biến đổi số ở dạng sau:
Cho hàm số f(x) liên tục trên đoạn [a;b]. Giả sử hàm số u=u(x) có đạo hàm liên tục trên đoạn [a;b] sao cho α ≤ u(x) ≤ β, ∀ x∈ [a;b]. Nếu f(x) =g[u(x)].u’(x) ∀ x∈ [a;b], trong đó g(u) liên tục trên đoạn [α;β] thì:
b. Phương pháp tính tích phân từng phần
Định lí. Nếu u =u(x) và v=v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a;b], thì :
hay
3. Bất đẳng thức (phần kiến thức bổ sung)
Nếu f(x) liên tục và không âm trên đoạn [a;b] thì :
Từ đó ta có:
Nếu g(x), f(x) liên tục trên đoạn [a;b] và 0 ≤ g(x) ≤ f(x), ∀ x ∈ [a;b] thì
Dấu " = " xảy ra khi và chỉ khi g(x) ≡ f(x).
Suy ra: Nếu f(x) liên tục trên đoạn [a;b] và m ≤ f(x) ≤ M, ∀ x ∈ [a;b] thì
Đặc biệt:
Nếu hàm y = f(x) là hàm số lẻ trên thì
Nếu hàm y = f(x) là hàm số chẵn trên thì
B. Tích phân các hàm số sơ cấp cơ bản
1. Tích phân hàm hữu tỉ
Dạng 1
(với a ≠ 0)
Chú ý: Nếu
Dạng 2
(ax2 + bx + c ≠ 0 với mọi x ∈ [α;β])
Xét Δ = b2 - 4ac.
• Nếu Δ > 0 thì
thì:
• Nếu Δ = 0 thì:
thì:
• Nếu Δ < 0 thì:
Dạng 3
(trong đó 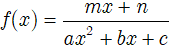
• Bằng phương pháp đồng nhất hệ số, ta tìm A và B sao cho:
• Ta có:
Tích phân:
Tích phân: 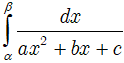
Dạng 4
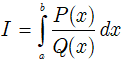
• Nếu bậc của P(x) lớn hơn hoặc bằng bậc của Q(x) thì dùng phép chia đa thức.
• Nếu bậc của P(x) nhỏ hơn bậc của Q(x) thì có thể xét các trường hợp:
• Khi Q(x) chỉ có nghiệm đơn α1, α2, α3 ... thì đặt
• Khi Q(x) có nghiệm đơn và vô nghiệm:
Q(x) = (x - α)(x2 + px + q), Δ = p2 - 4q < 0 thì đặt:
• Khi Q(x) có nghiệm bội:
Q(x) = (x - α)(x - β)2 với α ≠ β thì đặt:
Q(x) = (x - α)2(x - β)3 với α ≠ β thì đặt:
2. Tích phân hàm vô tỉ
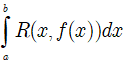
Dạng 1
Khi đó ta có:
• Nếu Δ < 0, a > 0 ⇒ f(x) = a(u2 + k2)
• Nếu: Δ = 0
• Nếu: Δ > 0
Với a > 0: f(x) = a(x - x1)(x - x2)
Với a < 0: f(x) = -a(x1 - x)(x2 - x)
Căn cứ vào phân tích trên, ta có một số cách giải sau:
Phương pháp:
* Trường hợp: Δ < 0, a > 0 ⇒ f(x) = a(u2 + k2)
Khi đó đặt:
* Trường hợp: Δ = 0
Khi đó:
* Trường hợp: Δ > 0, a > 0. Đặt:
* Trường hợp: Δ > 0, a < 0. Đặt:
Dạng 2
Phương pháp:
• Bước 1:
Phân tích:
• Bước 2:
Quy đồng mẫu số, sau đó đồng nhất hệ số hai tử số để suy ra hệ hai ẩn số A, B
• Bước 3:
Giải hệ tìm A, B thay vào (1)
• Bước 4:
Tính:
Trong đó 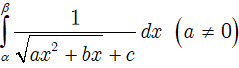
Dạng 3
Phương pháp:
• Bước 1:
Phân tích:
• Bước 2:
• Bước 3:
Thay tất cả vào (1) thì I có dạng:
Tích phân này chúng ta đã biết cách tính.
Dạng 4
(Trong đó: R(x,y) là hàm số hữu tỷ đối với hai biến số x, y và α, β, γ, δ là các hằng số đã biết)
Phương pháp:
• Bước 1:
Đặt:
• Bước 2:
Tính x theo t: Bằng cách nâng lũy thừa bậc m hai vế của (1) ta có dạng x = φ(t).
• Bước 3:
Tính vi phân hai vế: dx = φ'(t)dt và đổi cận.
• Bước 4:
Tính:
3. Tích phân hàm lượng giác
3.1. Một số công thức lượng giác
* Công thức cộng
* Công thức nhân đôi
* Công thức hạ bậc
* Công thức tính theo t
* Công thức biến đổi tích thành tổng
* Công thức biến đổi tổng thành tích
* Công thức thường dùng:
Hệ quả:
3.2. Một số dạng tích phân lượng giác
• Nếu gặp dạng 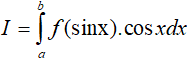
• Nếu gặp dạng 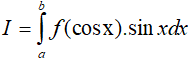
• Nếu gặp dạng 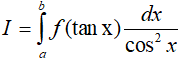
• Nếu gặp dạng 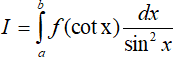
Dạng 1
I1 = ∫(sinx)n dx; I2 = ∫(cosx)n dx
* Phương pháp
• Nếu n chẵn thì sử dụng công thức hạ bậc.
• Nếu n = 3 thì sử dụng công thức hạ bậc hoặc biến đổi.
• Nếu n lẻ (n = 2p + 1) thì thực hiện biến đổi:
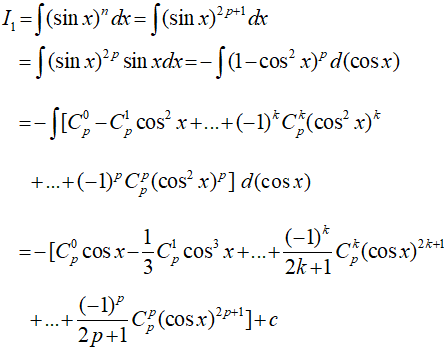
Dạng 2
I = ∫sinmx.cosnx dx (m, n ∈ N)
* Phương pháp
• Trường hợp 1: m, n là các số nguyên
a. Nếu m chẵn, n chẵn thì sử dụng công thức hạ bậc, biến đổi tích thành tổng.
b. Nếu m chẵn, n lẻ (n = 2p + 1) thì biến đổi:
c. Nếu m lẻ (m = 2p + 1), n chẵn thì biến đổi:
Dạng 3
I1 = ∫(tanx)n dx; I2 = ∫(cotx)n dx (n ∈ N)
C. Ứng dụng tích phân
1. Diện tích hình phẳng
a. Diện tích hình phẳng giới hạn bởi 1 đường cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x = a; x = b được xác định:
b. Diện tích hình phẳng giới hạn bởi 2 đường cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a;b] và hai đường thẳng x = a; x = b được xác định:
- Nếu trên đoạn [a;b], hàm số f(x) không đổi dấu thì:
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối.
- Diện tích của hình phẳng giới hạn bởi các đường x = g(y),x = h(y) và hai đường thẳng y = c; y = d được xác định:
2. Thể tích vật thể và thể tích khối tròn xoay
a. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm a (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a;b]. Thể tích của B là:
b. Thể tích khối tròn xoay
Cho hàm số y = f(x) liên tục; không âm trên [a;b]. Hình phẳng giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b quay quanh trục Ox tạo nên một khối tròn xoay. Thể tích của nó là:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục tung và hai đường thẳng y = c; y = d quay quanh trục Oy là:
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x); y = g(x) và hai đường thẳng x = a; x = b quay quanh trục Ox:
D. Bài tập vận dụng
Câu 1. Tính 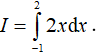
A. 6.
B. -3.
C. 3.
D. –6.
Lời giải
Ta có:
Chọn C.
Câu 2. Tính
A. e3 - e + 8.
B. e3 + e - 3.
C. e3 - e + 6.
D. e3 + 2e + 8.
Lời giải
Ta có:
Chọn A.
Câu 3. Cho 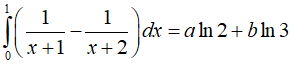
A. a + b = 0.
B. a - 2b = 0.
C. a - b = -1.
D. a + 2b = 0.
Lời giải
Ta có:
Chọn D.
Câu 4. Cho 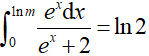
A. m = 1.
B. m = 2.
C. m = 4.
D. m = 0.
Lời giải
Điều kiện: m > 0.
Ta có:
Chọn C.
Câu 5. Tính
A. 0.
B. -1.
C. 1.
D. 2.
Lời giải
Ta có:
Chọn C.
Câu 6. Tính
A. 8 + 5ln3.
B. 6 - 5ln3.
C. 12 + 3ln5.
D. 11.
Lời giải
Ta có:
Chọn A.
Câu 7. Tính
A. 4.
B. 4ln2.
C. 4/ln2.
D. 6.
Lời giải
Ta có:
Chọn D.
Câu 8. Cho 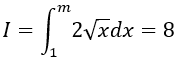
Lời giải
Ta có:
Chọn A.
Câu 9. Tính
A. 0.
B. 9.
C. 18.
D. -9.
Lời giải
Ta có:
Chọn B.
Câu 10. Tính
Lời giải
Ta có:
Chọn D.
Câu 11: Tính
Giải: Đặt
Suy ra
Tính
Ta đặt
Suy ra
Khi đó
Câu 12: Tính tích phân
Giải: Đặt
Khi đó
Câu 13: Tính
Giải: Đặt
Khi đó
Câu 14: Tính tích phân
Giải: Đặt
Khi đó