Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phương trình elip: Lý thuyết và các dạng bài tập, tài liệu bao gồm có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Phương trình elip: Lý thuyết và các dạng bài tập
1. Định nghĩa đường elip
Định nghĩa : Trong mặt phẳng, cho hai điểm cố định và
Elip là tập hợp các điểm sao cho tổng không đổi
Các điểm và gọi là tiêu điểm của elip
Khoảng cách gọi là tiêu cự của elip
2. Phương trình chính tắc của elip
Cho elip có tiêu điểm và chọn hệ trục tọa độ sao cho và . Khi đó người ta chứng minh được
elip + (1)
trong đó:
Phương trình (1) gọi là phương trình chính tắc của elip
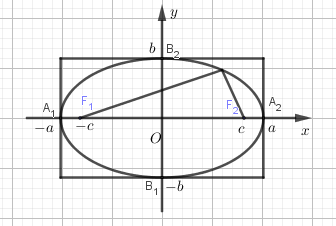
3. Hình dạng của elip
Xét elip có phương trình (1):
a) Nếu điểm thuộc thì các điểm và cũng thuộc .
Vậy có các trục đối xứng là và có tâm đối xứng là gốc .
b) Thay vào (1) ta có suy ra cắt tại hai điểm .
Tương tự thay vào (1) ta được , vậy cắt tại hai điểm .
Các điểm gọi là các đỉnh của elip.
Đoạn thẳng gọi là trục lớn, đoạn thẳng gọi là trục nhỏ của elip.
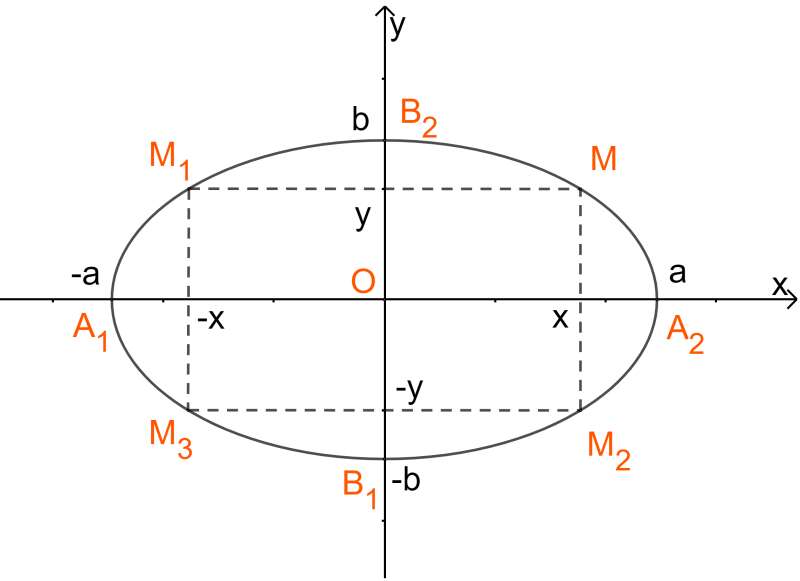
4. Phương pháp giải
Phương trình chính tắc của Elip
với .
Do đó điểm và , .
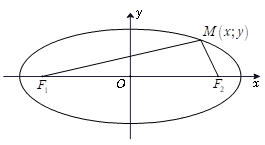
5. Bài tập ví dụ
Ví dụ 1: Biết Elip (E) có các tiêu điểm F1( - √7; 0), F2(√7; 0) và đi qua M(- √7;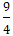 
) . Gọi N là 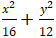điểm đối xứng với M qua gốc toạ độ. Khi đó
A. 
= 1 B. OM = 3
C. ON = 3 D. NF1 + MF1 = 8.
Hướng dẫn giải:
Ta có N đối xứng với M qua gốc tọa độ nên N(√7; - ) .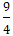
Suy ra: NF1 =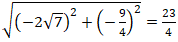 
; MF1 =
Từ đó: NF1 + MF1 = 8.
Chọn D.
Ví dụ 2: Cho elíp có phương trình 16x2 + 25y2 = 100.Tính tổng khoảng cách từ điểm thuộc elíp có hoành độ x = 2 đến hai tiêu điểm.
A. √3 B. 2√2 C. 5 D. 4√3
Hướng dẫn giải:
Ta có: 16x2 + 25y2 = 100 ⇔ 
Tổng khoảng cách từ một điểm bất kì thuộc Elip đến 2 tiêu điểm bằng 2a = 5.
Chọn C.
Ví dụ 3: Cho Elip (E): 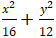= 1 và điểm M nằm trên (E). Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2 tiêu điểm của (E) bằng
A. 4 ± √2 B. 3 và 5. C. 3,5 và 4,5 . D. 4 ± 
Hướng dẫn giải
Ta có a2 = 16; b2 = 12 nên c2 = a2 - b2 = 4
⇒ a = 4; c = 2 và hai tiêu điểm F1 ( - 2;0); F2 (2;0).
Điểm M thuộc (E) và xM = 1 ⇒ yM = ± 
Tâm sai của elip e =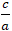 
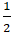
⇒ e = 
.
⇒ MF1 = a + exM = 4,5; MF2 = a - exM = 3,5
Chọn C.
Ví dụ 4: Cho elip (E):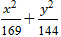 
= 1 và điểm M nằm trên (E). Nếu M có hoành độ bằng
- 13 thì khỏang cách từ M đến hai tiêu điểm bằng
A. 10 và 6 B. 8 và 18 C. 13 ± √5 D. 13 ± √10
Hướng dẫn giải
Từ dạng của elip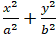 
= 1 ta có 
Suy ra: c2 = a2 – b2 = 25 nên c = 5.
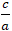
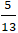
Tâm sai của elip e = ⇒ e = 
.
⇒ MF1 = a + exM = 8; MF2 = a - exM = 18
Chọn B.
Ví dụ 5: Cho elip (E):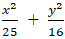 
= 1 , với tiêu điểm F1; F2. Lấy hai điểm A; B thuộc elip (E) sao cho AF1 + BF1 = 8. Khi đó, AF2 + BF2 = ?
A. 6 B. 8 C. 12 D. 10
Lời giải
+ Elip ( E): 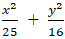= 1 có a2 = 25 nên a = 5
+ Do A ∈( E) nên AF1 + AF2 = 2a = 10.
+ Do B ∈( E) nên BF1 + BF2 = 2a = 10
⇒ AF1 + AF2 + BF1 + BF2 = 20
⇔ (AF1 + BF1 ) + (AF2 + BF2 ) = 20
⇔ 8 + (AF2 + BF2 ) = 20
⇔ AF2 + BF2 = 12
Chọn C.
Ví dụ 6: Cho elip (E):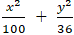 
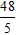
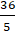
= 1. Qua một tiêu điểm của (E) dựng đường thẳng song song với trục Oy và cắt (E) tại hai điểm M và N. Tính độ dài MN.
A. 
B. 
C. 25 D. 
Lời giải
+ Xét elip (E): 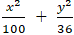= 1 có:
a2 = 100; b2 = 36 nên c2 = a2 – b2 = 64
+ Khi đó, Elip có tiêu điểm F1 ( - 8; 0)
⇒ đường thẳng d// Oy và đi qua F1 là x = - 8.
+ Giao điểm của d và (E) là nghiệm của hệ phương trình :
Vậy tọa độ hai giao điểm của d và (E) là M( - 8; 
) và N( - 8; - )
⇒ MN =
Chọn B.
Ví dụ 7: Cho ( E):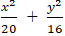 
= 1. Một đường thẳng đi qua điểm A(2; 2) và song song với trục hoành cắt (E) tại hai điểm phân biệt M và N. Tính độ dài MN.
A. 3√5 B. 15√2 C. 2√15 D. 5√3
Lời giải
+ Phương trình đường thẳng d: 
⇒ (d) có phương trình là y = 2
+ Ta có d cắt (E) tại M và N nên tọa độ M và N là nghiệm hệ phương trình:
⇒ Tọa độ hai điểm M( √15; 2);N( - √15; 2)
Vậy độ dài đoạn thẳng MN = 2√15 .
Chọn C.
Ví dụ 8: Cho elip: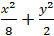 
= 1. Hỏi có bao nhiêu điểm thuộc elip có tọa độ nguyên?
A. 1 B. 4 C. 3 D. 8
Lời giải
Nếu điểm M(x; y) thuộc elip thì các điểm A( x; - y) ; B( - x; y) ; C( - x; - y) cũng thuộc elip. Do đó; ta xét điểm M có tọa độ nguyên dương.
Từ 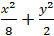= 1 ⇔ x2 = 8 - 4y2
Phương trình trên có nghiệm nếu: 8 - 4y2 ≥ 0
Kết hợp x; y > 0 nên 0 < y ≤ √2
⇒ y = 1 và x = 2.
⇒ Các điểm thuộc elip có tọa độ nguyên là: (2;1); (-2; 1); (2; -1) và ( -2; -1)
Chọn B.
Ví dụ 9: Cho elip: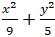 
= 1. Có bao nhiêu điểm M thuộc elip sao cho M nhìn hai tiêu điểm dưới một góc 600?
A. 1 B. 2 C. 3 D. 4
Lời giải
+ Ta có; a2 = 9; b2 = 5 nên c2 = a2 – b2 = 4
⇒ a = 3 và c = 2.
+ Elip có hai tiêu điểm là F1( - 2; 0) và F2 ( 2; 0)
+ Với mọi điểm M ta có: MF1 = a +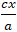 
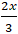
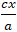
= 3 + 
; MF2 = a - = 3 -
MF1 + MF2 = 2a = 6
+ Xét tam giác MF1F2; áp dụng định lí cosin ta có:
F1F22 = MF12 + MF22 – 2. MF1. MF2. cosM
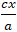
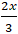
= [ ( MF1 + MF2)2 - MF1 = a + = 3 + ] – 2.MF1.MF2.cos600.
⇔ 42 = 62 – 3.MF1. MF2
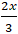
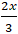
⇔ 16 = 36 - 3. (3 + ) .( 3 - )
⇔ 20 = 3. ( 9 -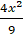 
) ⇔ x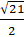2 = 
⇔ x = ± 
⇒ y = ± 
Vậy có bốn điểm thỏa mãn là:
Chọn D.
6. Bài tập vận dụng
Câu 1. Phương trình của elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:
A.
B.
C.
D.
Câu 2. Tìm phương trình chính tắc của elip có tiêu cự bằng 6 và trục lớn bằng 10.
A.
B.
C.
D.
Câu 3. Elip có độ dài trục lớn là 10 và có một tiêu điểm . Phương trình chính tắc của elip là:
A.
B.
C.
D.
Câu 4. Elip có độ dài trục nhỏ là và có một tiêu điểm . Phương trình chính tắc của elip là:
A.
B.
C.
D.
Câu 5. Elip có một đỉnh là và có một tiêu điểm . Phương trình chính tắc của elip là:
A.
B.
C.
D.
Câu 6. Elip có hai đỉnh là và có hai tiêu điểm là . Phương trình chính tắc của elip là:
A.
B.
C.
D.
Câu 7. Tìm phương trình chính tắc của elip nếu trục lớn gấp đôi trục bé và có tiêu cự bằng .
A.
B.
C.
D.
Câu 8. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị.
A.
B.
C.
D.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
