Tailieumoi.vn xin giới thiệu tới bạn đọc tài liệu về Tính chất tam giác vuông cân, tam giác vuông, tam giác cân, tam giác đều, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Tính chất tam giác vuông cân, tam giác vuông, tam giác cân, tam giác đều, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Tính chất tam giác vuông cân, tam giác vuông, tam giác cân, tam giác đều
A. Lý thuyết Tam giác
1. Tam giác vuông
a) Định nghĩa
Tam giác vuông là tam giác có một góc vuông.
b) Tính chất
Trong tam giác vuông hai góc nhọn phụ nhau.
Xét hình vẽ: Tam giác ABC vuông tại A
AB, AC là hai cạnh góc vuông, BC là cạnh huyền.
Ta có:
c) Dấu hiệu nhận biết
+ Nếu một tam giác có một góc vuông thì tam giác đó là tam giác vuông.
+ Nếu một tam giác có hai góc phụ nhau thì tam giác đó là tam giác vuông.
2. Tam giác cân
a) Định nghĩa
Tam giác cân là tam giác có hai cạnh bằng nhau.
Hai cạnh bằng nhau gọi là hai cạnh bên, cạnh còn lại là cạnh đáy.
b) Tính chất
+ Tam giác cân có hai cạnh bên bằng nhau.
+ Tam giác cân có hai góc ở đáy bằng nhau.
Xét hình vẽ
Tam giác ABC cân tại A ta có:
+ AB, AC là hai cạnh bên.
+ BC là cạnh đáy
Khi đó:
c) Dấu hiệu nhận biết:
+ Nếu một tam giác có hai góc bằng nhau thì tam gác đó là tam giác cân.
+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
3. Tam giác đều
a) Định nghĩa
Tam giác đều là tam giác có ba cạnh bằng nhau.
b) Tính chất
Nếu một tam giác là tam giác đều thì:
+ Ba góc của tam giác bằng nhau.
+ Ba cạnh của tam giác bằng nhau.
+ Số đo mỗi góc của tam giác là
Xét hình vẽ
Tam giác ABC là tam giác đều:
c) Dấu hiệu nhận biết
+ Nếu một tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.
+ Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
+ Nếu một tam giác cân có một góc bằng thì tam giác đó là tam giác đều.
4. Tam giác vuông cân
a) Định nghĩa
Tam giác vuông cân là tam giác có một góc vuông và hai cạnh góc vuông bằng nhau.
b) Tính chất
Nếu một tam giác là tam giác vuông cân thì nó có tất cả các tính chất của tam giác vuông và tam giác cân ngoài ra hai góc nhọn trong tam giác vuông cân sẽ bằng nhau và bằng .
Xét tam giác ABC vuông cân tại A ta có:
+ AB = AC
+
c) Dâu hiệu nhận biết
+ Tam giác vuông có hai cạnh góc vuông bằng nhau là tam giác vuông cân.
+ Tam giác vuông có một góc nhọn bằng là tam giác vuông cân.
+ Tam giác cân có một góc vuông là tam giác vuông cân.
B. Bài tập Tam giác
Bài tập vận dụng
Bài 1: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D; trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE cân.
Lời giải:
Vì tam giác ABC cân tại A nên (tính chất)
Vì là hai góc kề bù
(1)
Vì là hai góc kề bù
(2)
Mà (chứng minh trên) (3)
Từ (1); (2); (3)
Xét tam giác ABD và tam giác ACE có:
(chứng minh trên)
AB = AC (do tam giác ABC cân tại A)
BD = CE (giả thuyết)
Do đó (c – g – c)
(hai cạnh tương ứng)
Xét tam giác ADE có:
AD = AE (chứng minh trên)
Tam giác ADE cân tại A.
Bài 2: Cho tam giác ABC vuông tại A, . Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Tam giác BCD là tam giác gì? Vì sao?
b) Chứng minh BC = 2AC.
Lời giải:
a) Xét tam giác ABC vuông tại A có:
(định lý tổng ba góc trong một tam giác)
Xét tam giác ABD và tam giác ABC có:
AB chung
AD = AC (giả thuyết)
Do đó (c – g – c)
(hai cạnh tương ứng)
Xét tam giác BDC có:
BD = BC (chứng minh trên)
cân tại B
Mà có là tam giác đều.
b) Vì tam giác BDC là tam giác đều nên CD = BC
Xét tam giác BDA và tam giác BA có:
BA chung
BD = BC (do tam giác BDC đều)
Do đó (cạnh huyền – cạnh góc vuông)
Nên A là trung điểm của CD
Mà CD = BC nên (điều phải chứng minh).
Bài 3: Cho tam giác ABC vuông cân tại A. Trên các cạnh góc vuông AB và AC lấy các điểm D và E sao cho AD = AE. Qua D vẽ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh tam giác MDC cân.
Lời giải:
Xét tam giác ADC và tam giác AEB có:
AD = AE (giả thuyết)
AC = AB (do tam giác ABC vuông cân)
Do đó : (c – g – c)
(hai cạnh tương ứng). (1)
Gọi G là giao điểm của DK và BE
DG vuông góc với EB tại G.
Xét tam giác DGB vuông tại G có:
(tính chất)
(2)
Xét tam giác AEB vuông tại A có:
(tính chất)
(3)
Từ (2) và (3)
Lại có (đối đỉnh)
Nên
Xét hai tam giác AEB và tam giác ADM có:
AE = AD (giả thuyết)
Do đó: (góc nhọn – cạnh góc vuông)
(hai cạnh tương ứng) (4)
Từ (1) và (4) ta có DC = DM
Xét tam giác MDC có:
DM = DC (chứng minh trên)
Do đó tam giác MDC cân tại D.
Bài 4: Tìm các tam giác cân, vuông cân, đều trên hình vẽ sau:
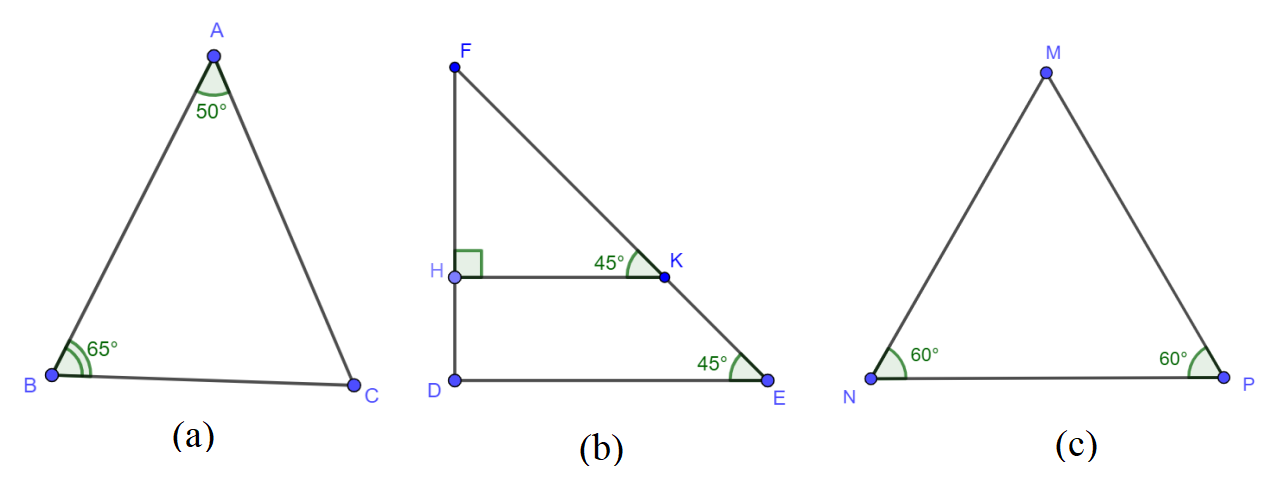
Giải:
(a) Áp dụng định lý góc ngoài trong tam giác ABC có:
có
Do đó cân tại A.
(b) Ta có, vuông tại H có
Nên là tam giác vuông cân tại H (1)
Vì
Mà hai góc này ở vị trí so le trong nên HK // DE
Vì , HK // DE
(Tính chất từ vuông góc đến song song)
Ta có, vuông tại D có
Nên là tam giác vuông cân tại D (2)
Từ (1) và (2) suy ra , là tam giác vuông cân.
(c) Áp dụng định lý tổng ba góc trong tam giác MNP có:
Ta có, có
Do đó là tam giác đều.
Bài 5: Cho tam giác ABC cân tại A (BC < AB). Trên cạnh AB lấy D sao cho CD = CB.
a) Chứng minh: .
b) Trên tia đối của tia CA lấy E sao cho CE = AD. Chứng minh BE = BA.
Giải:
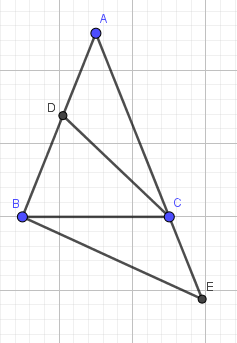
|
GT |
Cho , AB = AC (BC < AB) CD = CB (D CE là tia đối của tia CA: CE = AD |
|
KL |
a) b) BE = BA |
a) cân tại A nên
Vì cân tại C (do CD = CB) nên
Từ (1) và (2) suy ra
b) Ta có:
Mà (câu a)
Do đó:
Xét và có:
CE = AD (gt)
(cmt)
CD = CB (gt)
Do đó:
(hai cạnh tương ứng)
Mà AC = AB (do tam giác ABC cân tại A)
Vậy BE = AB (đpcm).
Bài 6: Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm khác phía đối với BC). Tính số đo góc BDA.
Giải:
|
GT |
(D và A nằm khác phía đối với BC) |
|
KL |
|
Xét và có:
AB = AC ( cân)
BD = CD ( đều)
Cạnh AD chung
Do đó:
(hai góc tương ứng)
Mặt khác, đều nên
Vậy .
Bài tập tự luyện
Bài 1: Câu nào đúng, câu nào sai? ( Đánh dấu x vào câu lựa chọn)
|
|
Đúng |
Sai |
|
a) Tam giác cân có một góc 45o là tam giác vuông cân. |
|
|
|
b) Mỗi góc ngoài của 1 tam giác thì bằng tổng 2 góc không kề nó của tam giác đó. |
|
|
|
c) Nếu tam giác có 1 cặp cạnh không bằng nhau thì tam giác đó không phải là tam giác cân. |
|
|
Bài 2: Cho tam giác ABC cân tại A, có . Tính các góc còn lại của tam giác đó.
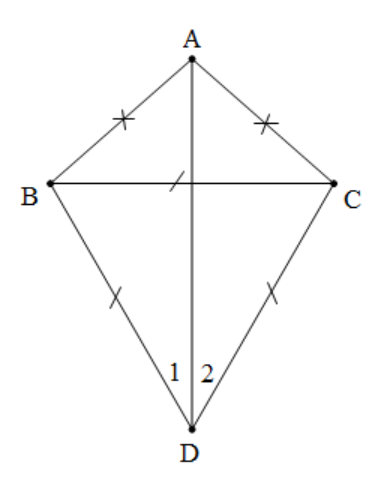
Bài 3: Số tam giác cân ở hình sau là:
A. 0
B. 1
C. 2
D. 3
Bài 4: Cho ∆ABC cân tại A. Lấy điểm E và F lần lượt thuộc các cạnh AB, AC sao cho BE = CF. Chứng minh AEF là tam giác cân.
Bài 5: Vẽ tam giác đều ABC có AB = AC = BC = 6cm
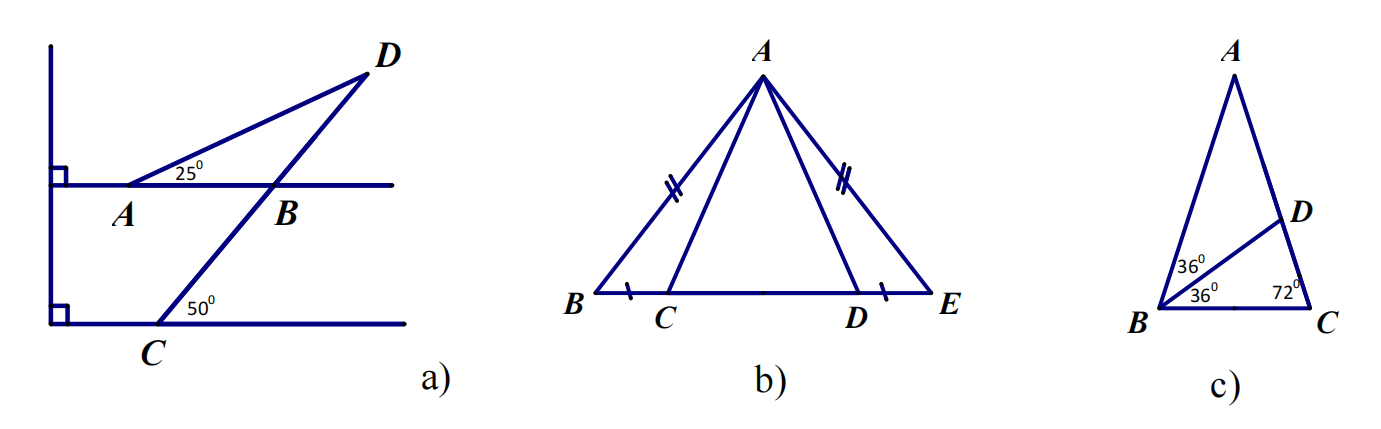
Bài 6: Tìm các tam giác cân trên hình vẽ sau:
Bài 7: Hai đường cao BE và CF của tam giác ABC cắt nhau tại O. Biết OC = AB.
a) Chứng minh .
b) Tính góc ACB.
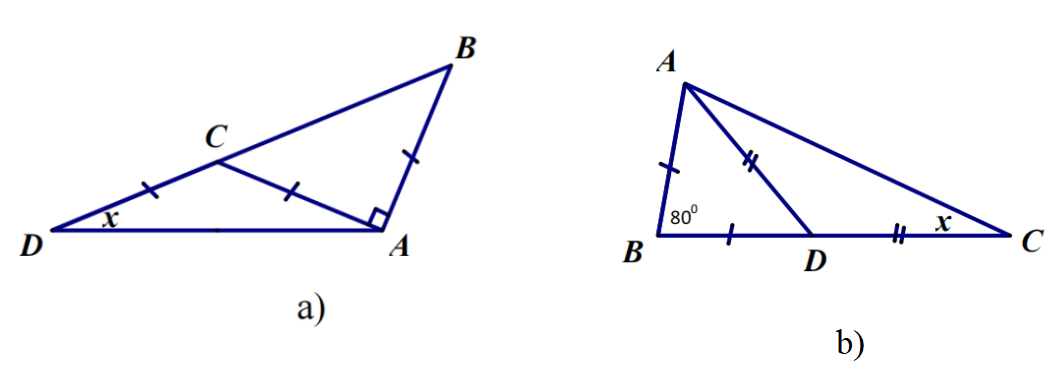
Bài 8: Tìm số đo x trên mỗi hình sau:
Bài 9: Cho cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh và là các tam giác cân.
Bài 10: Cho điểm M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC và BMD. Gọi E, F theo thứ tự là trung điểm của AD, CB. Chứng minh: MEF là tam giác đều.