Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Đường phân giác là gì? Tính chất đường phân giác của tam giác, tài liệu gồm đầy đủ về lý thuyết Đường phân giác, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Đường phân giác là gì? Tính chất đường phân giác của tam giác
A. Lý thuyết Đường phân giác
1. Khái niệm Đường phân giác
- Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.
- Mọi điểm trên một đường phân giác cách đều hai cạnh của góc đó và ngược lại.
2. Đường phân giác của tam giác
– Trong tam giác ABC (hình vẽ bên dưới), tia phân giác của cắt cạnh BC tại D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.
Đôi khi, đường thẳng AD cũng được gọi là đường phân giác của ∆ABC.
Ví dụ: Quan sát hình vẽ và chỉ ra các đường phân giác trong ∆ABC (nếu có):
Hướng dẫn giải
Quan sát hình vẽ trên, ta có:
và D là giao điểm của tia phân giác với cạnh BC. Do đó đoạn thẳng AD là đường phân giác của ∆ABC.
và F là giao điểm của tia phân giác với cạnh AB. Do đó đoạn thẳng CF là đường phân giác của ∆ABC.
Đoạn thẳng BE không là đường phân giác của ∆ABC vì BE không là tia phân giác của của tam giác ABC.
Nhận xét: Mỗi tam giác có ba đường phân giác.
Ví dụ:
∆ABC có ba đường phân giác AE; BF; CK xuất phát từ ba đỉnh của tam giác này.
3. Tính chất Đường phân giác của tam giác
Định lí: (Tính chất đường phân giác của tam giác) Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
Chứng minh định lí
Vẽ đường thẳng qua B, song song với AD, cắt đường thẳng AC tại E.
Theo giả thiết, AD là phân giác của góc A nên .
Ta có: EB // AD nên (hai góc so le trong);
(hai góc đồng vị).
Do đó: 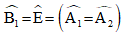
Suy ra: AE = AB (1).
Mặt khác, áp dụng định lí Thalès vào tam giác CEB, ta có:
(2).
Từ (1) và (2) ta suy ra: .
Chú ý: Trong tam giác ABC, nếu D là điểm thuộc đoạn BC và thỏa mãn thì AD là đường phân giác của góc A.
Ví dụ: Tính độ dài x trong hình dưới đây biết AM là đường phân giác của góc A.
Hướng dẫn giải
Trong tam giác ABC có AM là đường phân giác của góc A.
Do đó ta có:
.
Suy ra: x = .
4. Tính chất ba đường phân giác của tam giác
– Ba đường phân giác của một tam giác cùng đi qua một điểm
Nhận xét:
+ Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.
+ Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.
– Vậy, trong một tam giác ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.
Ví dụ: Cho ∆DEF có I là giao điểm của ba đường phân giác. Kẻ IH ⊥ EF tại H ; IK ⊥ DF tại K. Chứng minh rằng: IF là đường trung trực của đoạn thẳng HK.
Hướng dẫn giải
Theo bài ta có: IH ⊥ EF tại H; IK ⊥ DF tại K nên IH; IK lần lượt là khoảng cách từ điểm I tới cạnh EF và DF.
Mà I là giao điểm của ba đường phân giác của ∆DEF (giả thiết)
Do đó IH = IK (tính chất ba đường phân giác của tam giác)
Suy ra I nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng)(1)
Xét ∆IKF và ∆IHF có:
(IH ⊥ EF tại H ; IK ⊥ DF tại K),
IH = IK (chứng minh trên),
IF là cạnh chung.
Do đó ∆IKF = ∆IHF (cạnh huyền – cạnh góc vuông)
Suy ra FK = FH (hai cạnh tương ứng)
Suy ra F nằm trên đường trung trực của HK (tính chất đường trung trực của đoạn thẳng)(2)
Từ (1) và (2) suy ra I và F nằm trên đường trung trực của HK
Hay IF là đường trung trực của HK
Vậy IF là đường trung trực củađoạn thẳng HK.
B. Bài tập Đường phân giác
1. Bài tập trắc nghiệm
Bài 1: Hãy chọn câu đúng. Tỉ số của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.
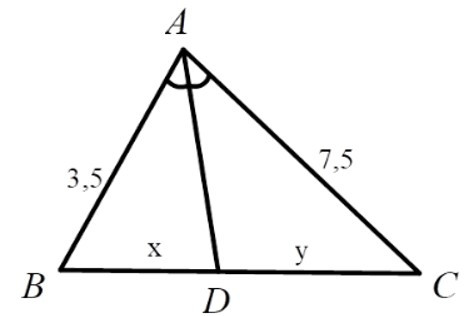
A.
B.
C.
D.
Đáp án: A
Giải thích:
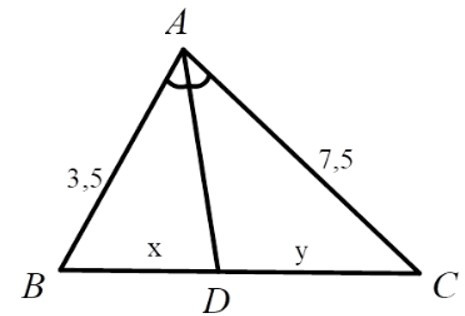
Xét tam giác ABC, vì AD là phân giác
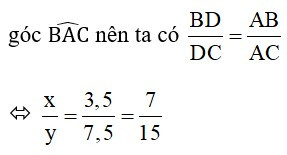
Bài 2: Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE.
1. Chọn khẳng định đúng.
A. DE // BC
B. DI = IE
C. DI > IE
D. Cả A, B đều đúng
Đáp án: D
Giải thích:
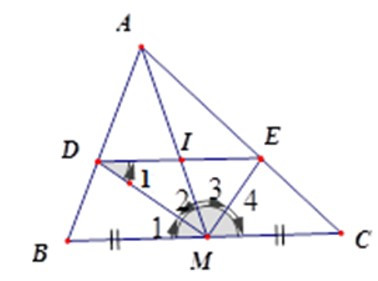
Vì MD và ME lần lượt là phân giác
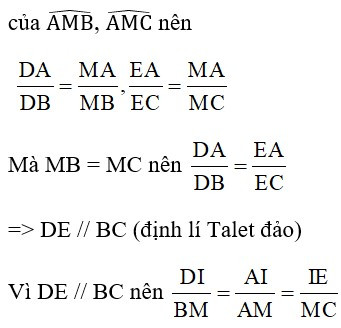
(hệ quả định lí Talet) mà BM = MC nên DI = IE.
Nên cả A, B đều đúng.
2. Tính độ dài DE, biết BC = 30cm, AM = 10cm.
A. 9cm
B. 6cm
C. 15cm
D. 12cm
Đáp án: D
Giải thích:
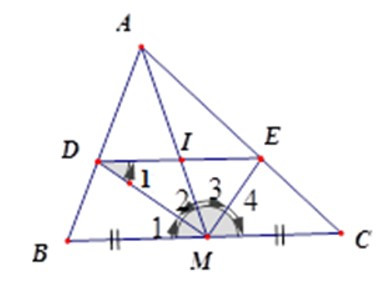
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù)
nên MI = DI = IE
Đặt DI = MI = x, ta có (cmt)
nên
Từ đó x = 6 suy ra DE = 12cm
Bài 3: Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức S = 49x2 + 98y2.
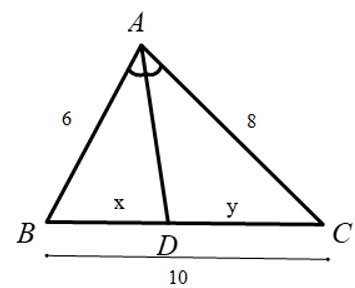
A. 3400
B. 4900
C. 4100
D. 3600
Đáp án: C
Giải thích:
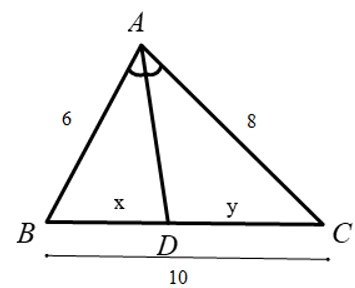
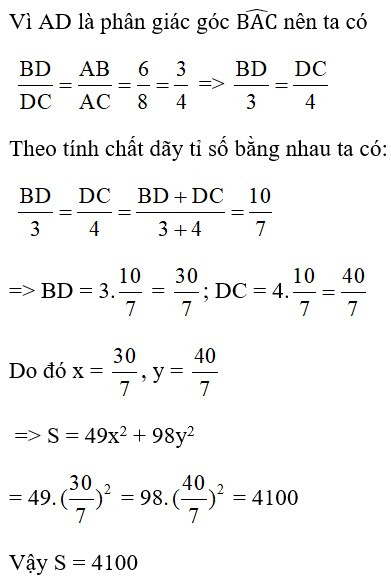
Bài 4: Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Tính BI?
A. 9cm
B. 6cm
C. 45cm
D. 3cm
Đáp án: D
Giải thích:
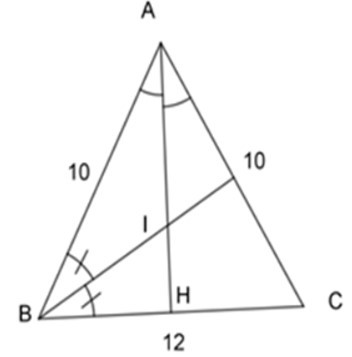
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:

Bài 5: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:
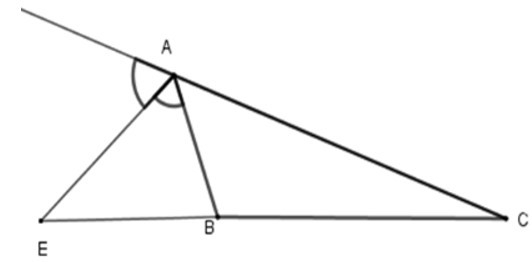
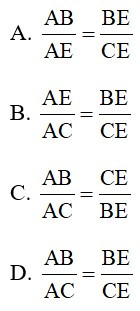
Đáp án: D
Giải thích:
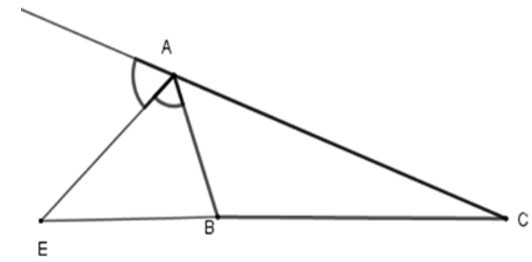
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên
Bài 6: Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Độ dài AI là:
A. 9cm
B. 6cm
C. 45cm
D. 3 cm
Đáp án: C
Giải thích:
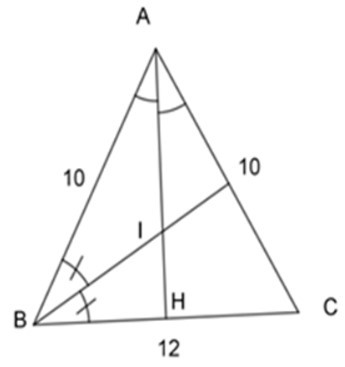
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
AH2 + BH2 = AB2

Bài 7: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:
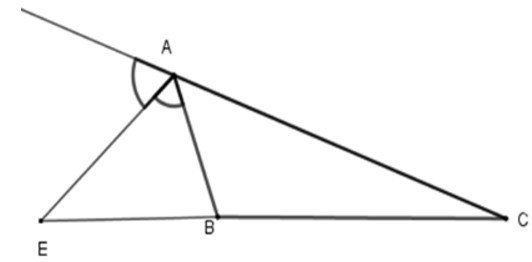
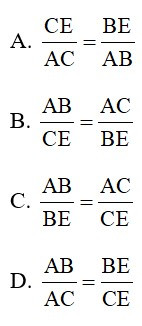
Đáp án: B
Giải thích:
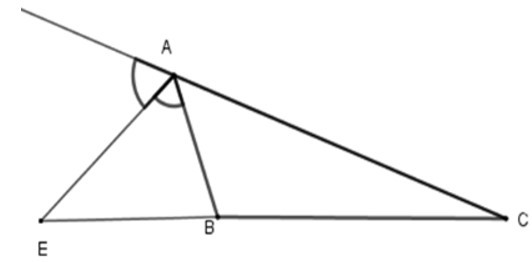
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy

Chỉ có B sai.
Bài 8: Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
A. 3cm
B. 6cm
C. 9cm
D. 12cm
Đáp án: C
Giải thích:
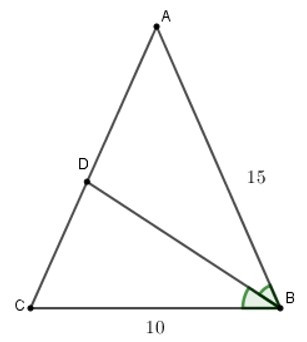
Vì BD là đường phân giác của

Bài 9: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:
A. 1,5
B. 3
C. 4,5
D. 4
Đáp án: B
Giải thích:
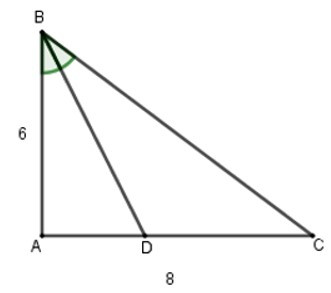
Tam giác ABC vuông tại A, áp dụng định lý Pytago có: BC2 = AB2 + AC2
BD là tia phân giác góc B

Bài 10: Cho tam giác ABC, = 900, AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của cắt HB tại D. Tia phân giác của cắt HC tại E. Tính HE?
A. 4cm
B. 6cm
C. 9cm
D. 12cm
Đáp án: B
Giải thích:
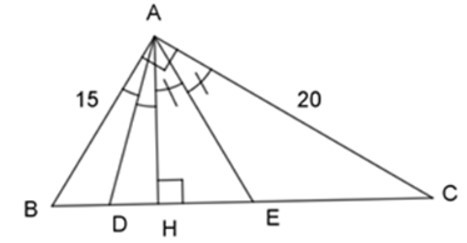
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
AB2 + AC2 = BC2

2. Bài tập vận dụng
Bài 1: Cho hình vẽ dưới đây.
a) Tính .
b) Tính x khi y = 5.
Hướng dẫn giải
a) Từ hình vẽ ta có AD là đường phân giác của góc A trong tam giác ABC.
Dựa vào tính chất đường phân giác của tam giác, ta có
.
Suy ra: .
b) Khi y = 5 thì x = .
Bài 2: Tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD và đường phân giác ngoài AE. Tính độ dài các đoạn thẳng DB, EB.
Hướng dẫn giải
Vì AD là đường phân giác trong của tam giác ABC, nên ta có
(1)
AE là đường phân giác ngoài của tam giác ABC, ta có:
(2)
Từ (1) và (2) suy ra: .
Từ , suy ra ⇒ DB = BC = . 10 = 4 (cm).
Từ , suy ra ⇒ EB = 2BC = 2 . 10 = 20 (cm).
Vậy DB = 4 cm và EB = 20 cm.
Bài 3: Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
Lời giải:
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
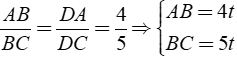
Áp dụng định lý Py – ta – go ta có:
BC2 = AC2 + AB2 hay ( 5t )2 = 92 + ( 4t )2 ⇔ ( 3t )2 = 92 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm
Bài 4: Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
Lời giải:
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
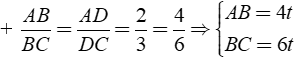
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15 (cm)
Bài 5. Cho ∆ABC có , AM là đường phân giác của đồng thời là đường trung tuyến. Qua M kẻ MH ⊥ AB tại H; MK ⊥ AC tại K. Chứng minh rằng ∆ABC là tam giác đều.
Hướng dẫn giải
Xét ∆AHM và ∆AKM có:
(vì MH ⊥ AB tại H; MK ⊥ AC tại K),
AM là cạnh chung,
(AM là đường phân giác của ).
Do đó ∆AHM = ∆AKM (cạnh huyền – góc nhọn)
Suy ra HM = KM (hai cạnh tương ứng)
Xét ∆BHM và ∆CKM có:
(vì MH ⊥ AB tại H; MK ⊥ AC tại K),
BM = CM (AM là đường trung tuyến của ∆ABC),
HM = KM (chứng minh trên).
Do đó ∆BHM = ∆CKM (cạnh huyền – cạnh góc vuông)
Suy ra (hai góc tương ứng)
Xét ∆ABC có suy ra ∆ABC cân tại A.
Ta lại có ∆ABC cân tại A có nên ∆ABC là tam giác đều.
Vậy ∆ABC là tam giác đều.
Bài 6. Cho ∆DEF cân tại D có và DM là đường trung tuyến. Tia phân giác của cắt DM ở N. Tính ?
Hướng dẫn giải
Xét ∆DEF có (tổng ba góc trong một tam giác)
Hay
Ta lại có (vì ∆DEF cân tại D)
Suy ra
Xét ∆DEM và ∆DFM có:
DE = DF (vì ∆DEF cân tại D),
DM là cạnh chung,
EM = FM (do M là trung điểm của EF),
DM là cạnh chung.
Vậy DDEM = DDFM (c.c.c)
Suy ra (hai góc tương ứng)
Do đó DM là đường phân giác của .
Lại có EN là đường phân giác của
Mà DM cắt EN tại N.
Do đó FN là đường phân giác của tam giác DEF.
Suy ra (tính chất tia phân giác)
Mà
Suy ra
Vậy .
Bài 7. Cho ∆ABC các tia phân giác của và cắt nhau tại điểm O. Qua O kẻ đường thẳng song song với BC cắt AB tại M, cắt AC ở N. Cho BM = 4 cm, CN = 5 cm. Tính độ dài đoạn thẳng MN.
Hướng dẫn giải
Vì O là giao điểm các tia phân giác của và nên CO là tia phân giác
Suy ra (1)
Mà (hai góc so le trong vì MN // BC) (2)
Từ (1) và (2) suy ra suy ra ∆NOC cân tại N.
Nên NO = NC.
Vì BO là phân giác của suy ra (3)
Do MN // BC nên (hai góc ở vị trí so le trong) (4)
Từ (3) và (4) suy ra suy ra ∆MBO cân tại B
Suy ra MB = MO.
Ta có MN = MO + ON = MB + NC (vì NO = NC; MB = MO)
Hay MN = 4 + 5 = 9 (cm).
Vậy MN = 9 cm.
Bài 8. Cho ∆ABC vuông tại A có I là giao điểm của ba đường phân giác trong tam giác. Gọi E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC. Chứng minh IE = IF = EA = FA.
Hướng dẫn giải
Theo bài ta có: I là giao điểm của ba đường phân giác trong ∆ABC.
Do đó AI là phân giác hay .
Suy ra (tính chất tia phân giác)
Mà nên
∆AEI vuông tại E có nên ∆AEI vuông cân tại E.
Suy ra EA = EI (tính chất tam giác cân) (1)
∆AFI vuông tại F có nên ∆AFI vuông cân tại F.
Suy ra FA = FI (tính chất tam giác cân) (2)
Do I là giao điểm của ba đường phân giác trong ∆ABC và IE; IF lần lượt là khoảng cách từ I đến cạnh AB; AC (vì E, F là chân các đường vuông góc kẻ từ I đến cạnh AB và AC)
Nên IE = IF (tính chất ba đường phân giác trong tam giác) (3)
Từ (1), (2) và (3) suy ra IE = IF = EA = FA.
Vậy IE = IF = EA = FA.