Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh Hàm số liên tục là gì? Lý thuyết và các dạng bài tập có đáp án chi tiết, chọn lọc. Tài liệu gồm có lý thuyết và các dạng bài tập cực hay bám sát chương trình sgk Toán 11. Hi vọng với Hàm số liên tục là gì? Lý thuyết và các dạng bài tập có đáp án này sẽ giúp bạn ôn luyện kiến thức để đạt kết quả cao trong bài thi môn Toán 11 sắp tới.
Hàm số liên tục là gì? Lý thuyết và các dạng bài tập
1. Hàm số liên tục tại một điểm
Định nghĩa 1
Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K.
Hàm số y = f(x) được gọi là liên tục tại x0 nếu 
2. Hàm số liên tục trên một khoảng
Định nghĩa 2
Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
Hàm số liên tục trên khoảng (a;b)
Hàm số không liên tục trên khoảng (a; b).
3. Một số định lí cơ bản
Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Định lí 2
Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0;
b) Hàm số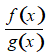 
liên tục tại x0 nếu g(x0) ≠ 0.
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0..
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
4. Các dạng bài tập về Hàm số liên tục
4.1 Cách xét tính liên tục của hàm số
*Phương pháp giải
Vấn đề 1: Xét tính liên tục của hàm số tại một điểm
- Cho hàm số y = f(x) có tập xác định D và điểm x0 ∈ D. Để xét tính liên tục của hàm số trên tại điểm x = x0 ta làm như sau:
+ Tìm giới hạn của hàm số y = f(x) khi x → x0 và tính f(x0)
+ Nếu tồn tại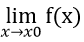 
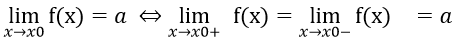
thì ta so sánh
với f(x0).
Nếu 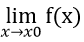= f(x0) thì hàm số liên tục tại x0
Chú ý:
1. Nếu hàm số liên tục tại x0 thì trước hết hàm số phải xác định tại điểm đó.
2.
3. Hàm số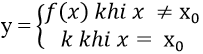 
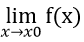
liên tục tại x = x0 ⇔ = k
4. Hàm số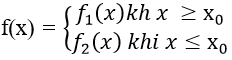 
liên tục tại điểm x = x0 khi và chỉ khi 
Vấn đề 2: Xét tính liên tục của hàm số trên một tập
Ta sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm chia của các khoảng đó.
*Ví dụ minh họa
Bài 1: Xét tính liên tục của hàm số sau tại x = 3
Hướng dẫn:
1. Hàm số xác định trên R
Ta có f(3) = 10/3 và
Vậy hàm số không liên tục tại x = 3
2. Ta có f(3) = 4 và
Vậy hàm số gián đoạn tại x = 3
Bài 2: Xét tính liên tục của các hàm số sau trên toàn trục số
1. f(x) = tan2x + cosx
Hướng dẫn:
1. TXĐ: 
Vậy hàm số liên tục trên D
2. Điều kiện xác định:
Vậy hàm số liên tục trên (1;2) ∪ (2,+∞)
Bài 3: Xét tính liên tục của hàm số sau tại điểm chỉ ra
Hướng dẫn:
Ta có
Vậy hàm số liên tục tại x = 1
Bài 4: Xét tính liên tục của hàm số sau tại điểm chỉ ra
Hướng dẫn:
Vậy hàm số không liên tục tại điểm x = -1
Bài 5: Chọn giá trị f(0) để các hàm số sau liên tục tại điểm x = 0
Hướng dẫn:
Bài 6: Xét tính liên tục của các hàm số sau tại điểm đã chỉ ra
Hướng dẫn:
Ta có:
Vậy hàm số gián đoạn tại x = -1
Bài 7: Xét tính liên tục của các hàm số sau tại điểm đã chỉ ra
Hướng dẫn:
Ta có
Vậy hàm số liên tục tại x = 1
4.2 Cách tìm m để hàm số liên tục
*Phương pháp giải
Ta sử dụng điều kiện để hàm số liên tục và điều kiện để phương trình có nghiệm để làm các bài toán dạng này.
- Điệu kiện để hàm số liên tục tại x0:
- Điều kiện để hàm số liên tục trên một tập D là f(x) liên tục tại mọi điểm thuộc D.
- Phương trình f(x) = 0 có ít nhất một nghiệm trên D nếu hàm số y = f(x) liên tục trên D và có hai số a, b thuộc D sao cho f(a).f(b) < 0.
Phương trình f(x) = 0 có k nghiệm trên D nếu hàm số y = f(x) liên tục trên D và tồn tại k khoảng rời nhau (ai ; ai+1) (i = 1,2,…,k) nằm trong D sao cho f(ai).f(ai+1) < 0.
*Ví dụ minh họa
Bài 1: Xác định a để hàm số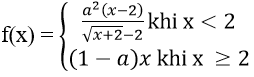 
liên tục trên R.
Hướng dẫn:
Hàm số xác định trên R
Với x < 2 ⇒ hàm số liên tục
Với x > 2 ⇒ hàm số liên tục
Với x = 2 ta có
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 2
Vậy a = -1, a = 0.5 là những giá trị cần tìm.
Bài 2: Cho hàm số f(x) = x3 – 1000x2 + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ?
I. (–1; 0) II. (0; 1) III. (1; 2)
Hướng dẫn:
Ta có hàm số y = f(x) = x3 – 1000x2 + 0,01 là hàm liên tục trên R
f(0) = 0.01 và f(-1) = - 1001 + 0.01 < 0. Nên f(0).(-1) < 0.
Vậy hàm số có nghiệm trong khoảng I
Bài 3: Tìm m để các hàm số sau liên tục trên R
Hướng dẫn:
Với x < 0 ⇒ hàm số liên tục
Với x > 0 ⇒ hàm số liên tục
Với x = 0 ta có
Hàm số liên tục trên R ⇔ hàm số liên tục tại x = 0
Bài 4: Chứng minh rằng phương trình sau có ít nhất một nghiệm :
x7 + 3x5 - 1 = 0
Hướng dẫn:
Ta có hàm số f(x) = x7 + 3x5 - 1 liên tục trên R và f(0).f(1) = - 3 < 0
Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0,1).
Bài 5: Chứng minh rằng phương trình sau có ít nhất một nghiệm :
x2sinx + xcosx + 1 = 0
Hướng dẫn:
Ta có hàm số f(x) = x2sinx + xcosx + 1 liên tục trên R và f(0).f(π) = -π < 0. Suy ra phương trinh f(x) = 0 có ít nhất một nghiệm thuộc (0 ; π).
Bài 6: Xác định a, b để các hàm số sau liên tục trên R
Hướng dẫn:
Ta có hàm số đã cho liên tục trên R\{π/2} do các hàm y = sinx và y = ax + b lên tục trên R.
Ta chỉ cần xét tính liên tục của hàm số tại x = π/2.
Vậy a, b là số thực thỏa mãn phương trình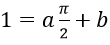 
thì hàm số đã cho liên tục trên R.
Bài 7: Tìm m để các hàm số sau liên tục trên R
Hướng dẫn:
Hàm số xác định trên R
Với x < 2 ⇒ hàm số liên tục
Với x > 2 ⇒ hàm số liên tục
Với x = 2 ta có
⇔ m = 3
Vậy m = 3 là giá trị cần tìm
Bài 8: Xác định a,b để các hàm số sau liên tục trên R
Hướng dẫn:
Với x ≠ 2 và x ≠ 0 hàm số liên tục.
Để hàm số đã cho liên tục trên R thì hàm số phải liên tục tại x = 2 và x = 0
Vậy a = 1 và b = -1 thì hàm số liên tục trên R
5. Bài tập tự luyện
Câu 1: Cho phương trình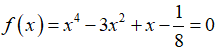 
(1) .Chọn khẳng định đúng:
A. Phương trình (1) có đúng một nghiệm trên khoảng (-1; 3).
B. Phương trình (1) có đúng hai nghiệm trên khoảng (-1; 3).
C. Phương trình (1) có đúng ba nghiệm trên khoảng (-1; 3).
D. Phương trình (1) có đúng bốn nghiệm trên khoảng (-1; 3).
Do đó phương trình có ít nhất 4 ngiệm thuộc khoảng (-1; 3).
Mặt khác phương trình bậc 4 có tối đa bốn nghiệm.
Vậy phương trình có đúng 4 nghiệm thuộc khoảng (-1; 3).
Chọn đáp án D
Câu 2: Cho hàm số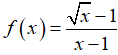 
. Tìm khẳng định đúng trong các khẳng định sau:
A. Chỉ (I).
B. Chỉ (III)
C. Chỉ (I) và (III)
D. Chỉ (II) và (III)
Chọn đáp án C
Câu 3: Cho hàm số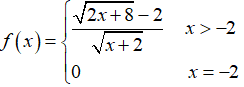 
. Tìm khẳng định đúng trong các khẳng định sau:
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II)
Chọn đáp án B
Câu 4: Cho hàm số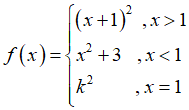 
. Tìm k để f(x) gián đoạn tại x= 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
Chọn đáp án A
Câu 5: Cho hàm số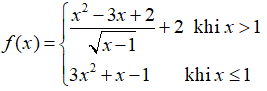 
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x = 1
D. Tất cả đều sai
Chọn đáp án C
Câu 6: Cho hàm số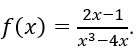 
Kết luận nào sau đây là đúng?
A. Hàm số f(x) liên tục tại điểm x = -2
B. Hàm số f(x) liên tục tại điểm x = 0
C. Hàm số f(x) liên tục tại điểm x = 0,5
D. Hàm số f(x) liên tục tại điểm x = 2
Hàm số đã cho không xác định tại x = 0, x = -2, x = 2 nên không liên tục tại các điểm đó. Hàm số liên tục tại x = 0,5 vì nó thuộc tập xác định của hàm phân thức f(x).
Chọn đáp án C
Câu 7: Cho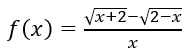 
với x ≠ 0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x=0?
Chọn đáp án C
Câu 8: Cho hàm số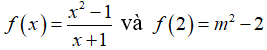 
với x ≠ 2 . Giá trị của m để f(x) liên tục tại x =2 là:
Chọn đáp án C
Câu 9: Cho hàm số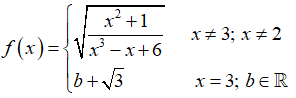 
. Tìm b để f(x) liên tục tại x = 3.
Chọn đáp án D
Câu 10: Cho hàm số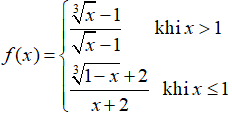 
. Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên R
B. Hàm số không liên tục trên R
C. Hàm số không liên tục trên (1; +∞)
D. Hàm số gián đoạn tại các điểm x= 1.
Chọn đáp án A
Câu 11: Chọn giá trị f(0) để các hàm số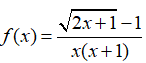 
liên tục tại điểm x= 0.
A. 1
B. 2
C. 3
D. 4
Chọn đáp án A
Câu 12: Cho hàm số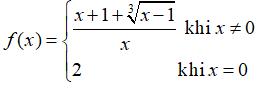 
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x0 = 0
B. Hàm số liên tục tại mọi điểm nhưg gián đoạn tại x0 = 0
C. Hàm số không liên tục tại x0 = 0
D. Tất cả đều sai
Chọn đáp án A
Câu 13: Cho hàm số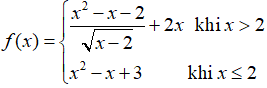 
. Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x0 = 2
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x0 = 2
D. Tất cả đều sai
Chọn đáp án C
Câu 14: Cho hàm số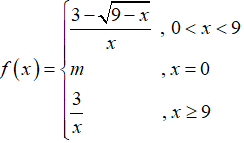 
. Tìm m để f(x) liên tục trên [0; +∞) là.
A. 1/3
B. 1/2
C. 1/6
D. 1
Chọn đáp án C
Câu 15: Cho hàm số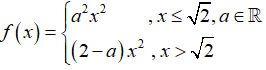 
. Giá trị của a để f(x) liên tục trên R là:
A. 1 và 2.
B. 1 và -1
C. -1 và 2.
D. 1 và -2
Chọn đáp án D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
